太陽能無人機能源系統參數的敏度分析

楊宇丹， 朱炳杰， 郭 正， 楊希祥

(國防科技大學 空天科學學院， 長沙 410073)

太陽能無人機(UAV)工作在高度適中、氣流平穩的臨近空間，彌補了航空器與航天器之間的高度空缺，將太陽能作為能源不但可以保護環境，在理論上還可以實現永續飛行.此外，研究太陽能無人機在充分開發與利用臨近空間、搶占發展機遇方面有著重要作用.因此，太陽能無人機受到了世界各國的廣泛關注.另外，研究太陽能無人機對于我國的軍事與民用發展也有著助推加速的戰略作用.

André[1]曾完整地建立了一套太陽能飛行器的總體設計方法，該方法通過近似建模將所有參數都表示為與飛行器質量有關的函數，使得模型之間的關系更加清晰明確.Sineglazov等[2]采用由André建立的飛行器總體設計方法，通過進一步研究對太陽能飛行器的能源系統進行了初步設計.

Rajendran等[3]系統地研究了影響太陽輻照度的因素，并通過仿真實驗詳細地分析了各因素之間的相互關系.Wang等[4]通過建立太陽電池曲面模型，研究了太陽能飛行器姿態變化對電池產能的影響.昌敏等[5]以跨晝夜能量平衡、日間能量充放平衡和夜間能量消耗為基礎，從多個角度分析了各參數對巡航高度的影響.

文獻[1-2]的研究主要針對太陽能飛行器的總體設計，而對能源系統及其參數的敏度分析較少.文獻[3-5]的研究則從各個角度對能源系統進行了分析研究，但飛行器的設計參數對能源系統模型的影響并未進行系統性的分析.太陽能飛行器的質量、翼展、展弦比等因素對能源系統模型的建立具有一定的影響，而能源系統模型的設計對飛行器的總體設計具有一定的制約作用.因此，對于能源系統模型及其參數敏度的分析研究具有較大的實際應用價值.本文主要參照現有的太陽能無人機能源系統模型，著重對能源系統的參數敏度進行分析討論，確定滿足飛行需求的無人機相關參數，為太陽能無人機能源系統以及整體設計提供依據.

1 太陽能無人機的工作原理

太陽能無人機利用鋪裝在機翼上的太陽電池板獲取能量，提供飛行過程中的能源消耗.白天太陽電池板將太陽輻照轉化為電能，一部分直接供給無人機飛行，另一部分儲存在蓄電池中，供無人機的夜間飛行使用，具體的能源分配如圖1所示.其中：P為功率，包括飛行器消耗功率以及太陽電池發電功率；t為時間.

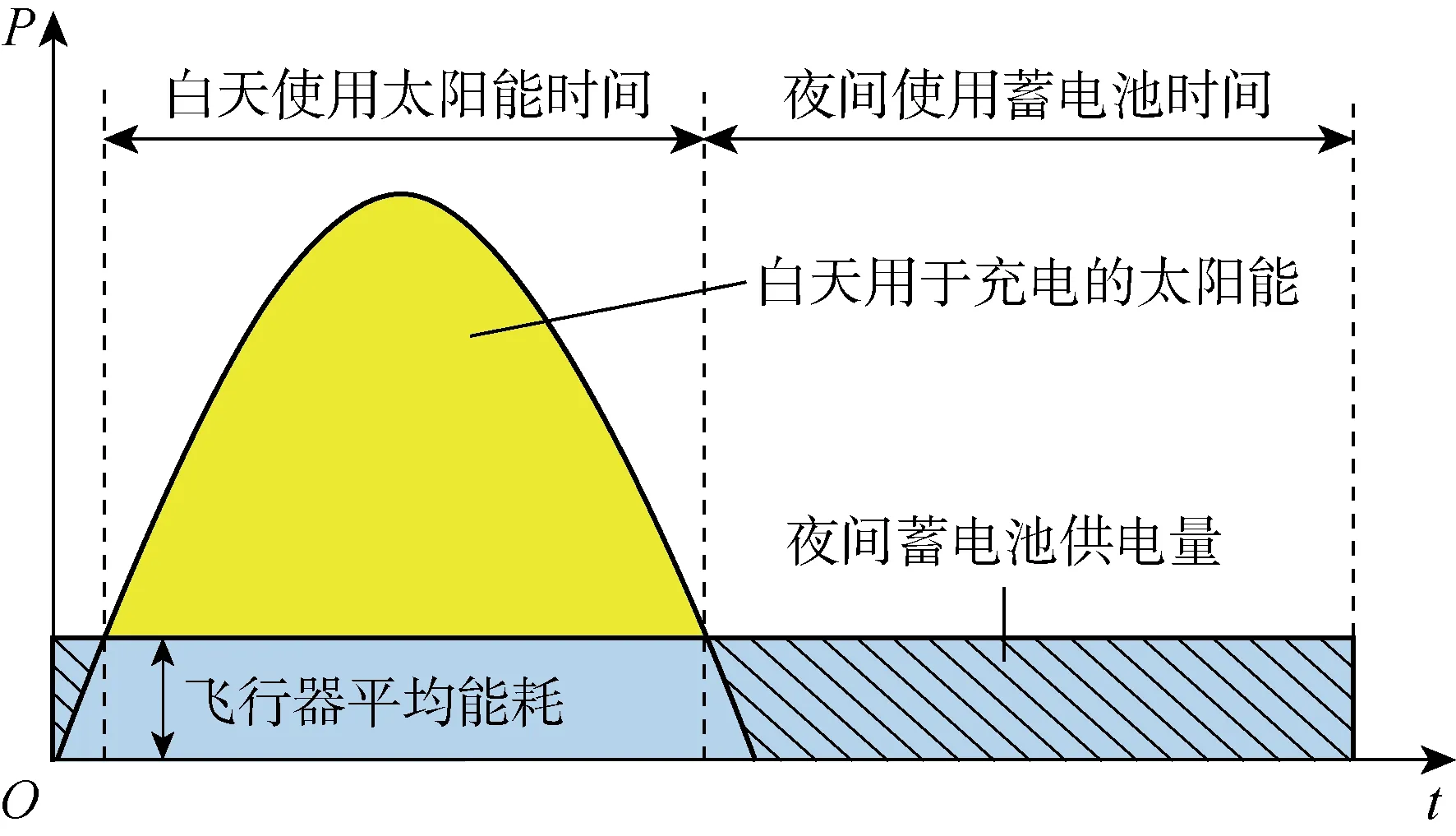
圖1 太陽能無人機的能量特性Fig.1 Energy characteristics of solar powered UAV

根據預設的任務規劃， 太陽能無人機飛行剖面一般可劃分為起飛-爬升-巡航、跨晝夜飛行和下滑著陸3個階段[6].

在起飛-爬升-巡航階段，太陽能無人機從地面起飛，經過持續爬升到達指定的高度后轉為巡航平飛.

持續跨晝夜飛行可以分為4個子階段，如圖2所示，其中h為飛行高度.

(1) 白天巡航階段：太陽能無人機在預設高度保持平飛.

(2) 傍晚下降階段：當太陽能電池提供的電能無法維持巡航功率需求時，采用降低飛行高度轉換為重力勢能的飛行策略.

(3) 夜間巡航階段：當飛行高度下降至預設高度時，太陽能無人機開始夜間平飛.

(4) 上午爬升階段：日出時，太陽能電池開始供能，無人機向白天巡航高度爬升.

在下滑著陸階段，太陽能無人機完成既定任務后開始下降并著陸.

在3個任務階段中，下降著陸階段對能量的要求較低，而起飛-爬升-巡航階段的能耗關系與持續跨晝夜飛行階段中的上午爬升與白天巡航階段相似，故本文著重分析太陽能無人機在持續跨晝夜飛行階段的能耗關系.

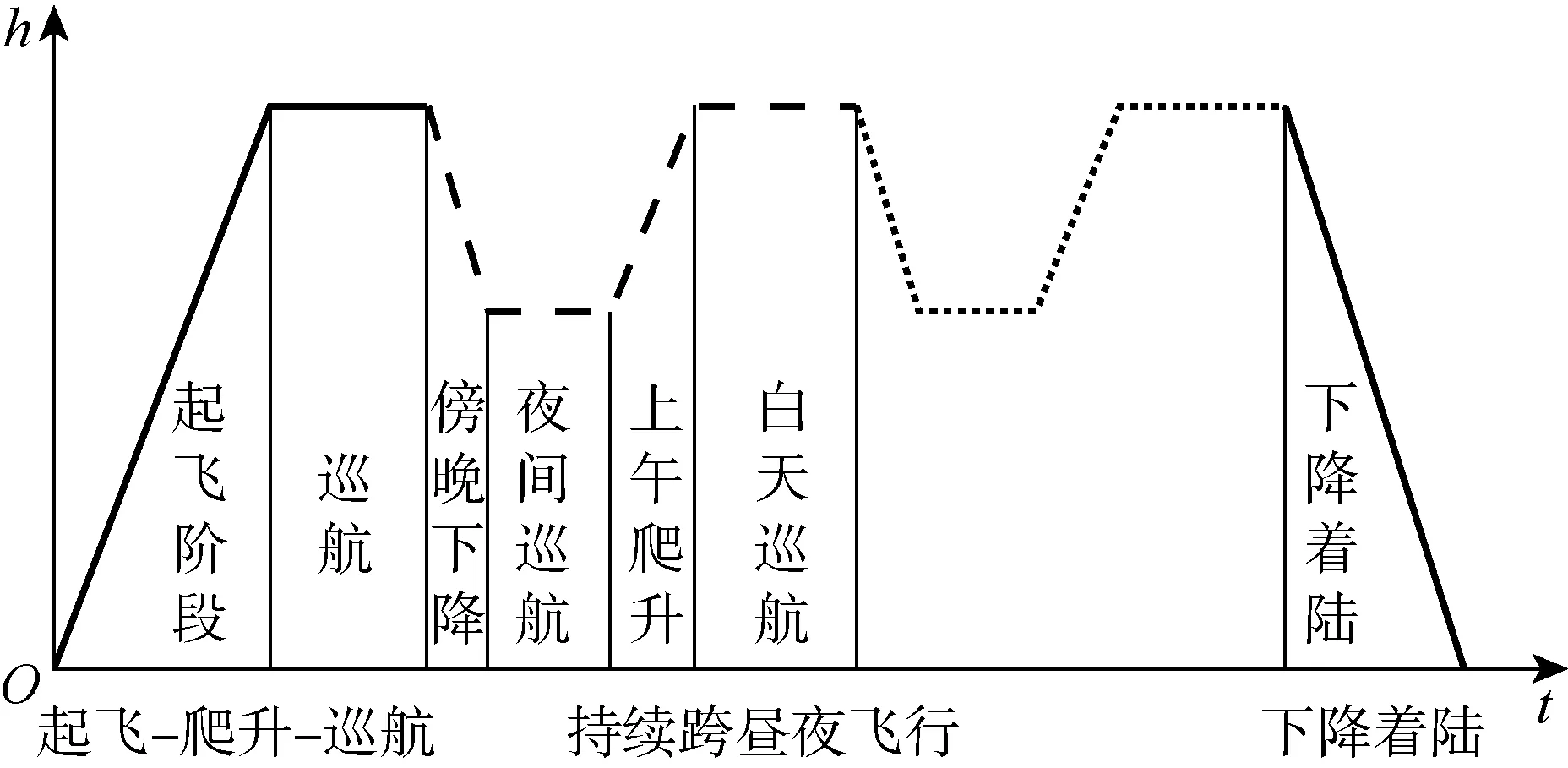
圖2 太陽能無人機的典型飛行剖面Fig.2 Classical flight profile of solar powered UAV

2 能源系統建模

2.1 各飛行階段功率建模

在日間和夜間巡航階段，太陽能無人機在空中進行穩定的水平飛行，機翼升力抵消了飛機重力，螺旋槳推力抵消了阻力，即滿足升重平衡以及推阻平衡[7-8]，則有

式中：m為太陽能無人機質量；g為重力加速度，本文中取為定值；CL為升力系數；CD為阻力系數；ρ為大氣密度；S為機翼參考面積；v為無人機速度；T為螺旋槳推力.由式(1)可推導出速度表達式為

(3)

將式(3)代入式(2)可求得水平飛行功率為

(4)

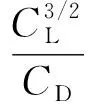
日落時，為減少儲能電池的供能負擔，采用僅依靠重力滑翔的方式進行飛行，儲能電池僅為航電系統以及載荷供電方式，即滑翔過程中動力推進系統的功率Pgli≈0.

太陽能無人機下降到一定高度后進行巡航平飛，夜間巡航與白天巡航高度不同，所以在這兩個階段之間要進行爬升.為了減小儲能電池的容量需求，選取日出時刻為太陽能無人機爬升的起始時刻，太陽能電池開始發電，飛行過程中由太陽能電池和儲能電池混合供電.由于太陽高度角會隨時間發生變化，為接收更多的太陽輻照，太陽能無人機應不斷調整自身的俯仰角和攻角.

在爬升過程中，假設無人機攻角和俯仰角保持不變.為了使螺旋槳消耗的功率盡量小，無人機應該勻速爬升，即飛行過程中應當受力平衡.不考慮風速影響，太陽能無人機的受力分析如圖3所示[9].其中：α為攻角；θ為俯仰角；L為升力；D為阻力.由圖3可以知道，沿速度方向和垂直于速度方向進行受力分析，則有

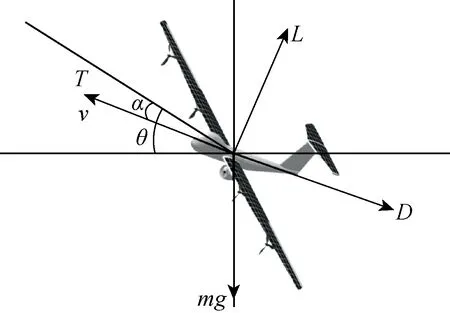
圖3 爬升階段受力分析[9]Fig.3 Forces applied for aircraft climbing[9]

(5)

L=mgcos(θ-α)

(6)

可求得速度表達式為

(7)

爬升功率Pcli為

(8)

由式(8)可以看出，爬升功率主要受到功率因子、無人機質量、機翼參考面積、大氣密度以及爬升的俯仰角和攻角的影響.

2.2 無人機日均所需功率

通過上述分析可以獲得每個飛行階段推進系統的所需功率.另外，太陽能無人機上航電系統與有效載荷時時需要消耗能量，據此可以獲得太陽能無人機的日均所需功率為

(9)

式中：Pav為航電系統消耗的功率；Ppld為有效載荷消耗的功率；Plev,d為白天巡航功率；Plev,n為夜間巡航功率；ηbec為電壓電流的轉換效率；ηmot為電機的效率；ηprl為螺旋槳的效率；td為白天巡航時間；tn為夜間巡航時間；tgli為滑翔時間.由于爬升階段功率隨著高度的變化而變化，爬升高度可表示為時間的函數，所以式(9)中爬升階段的能耗可用積分形式表示.其中，傍晚下滑時只利用重力勢能，故其功率Pgli可忽略不計；上午爬升時由于太陽輻照較弱，主要靠儲能電池供電，參照文獻[9]的能源系統建模法，可獲得爬升階段的最優俯仰角、攻角和爬升時間.簡化后的日均所需功率為

(10)

太陽能無人機提供的功率為

(11)

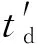
由式(11)可知，每日由太陽能電池所獲取的能量經過轉換可以供給太陽能無人機使用的平均功率，主要由太陽輻照強度、日照時間、太陽電池鋪裝面積等因素決定，并且與太陽輻照強度以及鋪裝面積成正比.Esc與太陽高度角、太陽方位角、緯度、時角、赤緯角以及大氣透射率等參數都有著密切的關系，具體建模過程可以參考文獻[9-11].

為使無人機正常飛行，所需功率與可提供的功率需滿足以下關系：

Pne≤Pprov

(12)

即所需功率要小于等于可提供的功率.

3 參數敏度分析模型

為提高模型精度，需進行相關參數的敏度研究[12-14].將展弦比AR=b2/S(b為太陽能無人機的展長)代入式(4)以及爬升功率表達式(8)中，則有

(13)

(14)

3.1 功率因子對所需功率的影響

預設飛行高度：白天巡航高度為20 km，夜間巡航高度為12 km.將平飛功率以及爬升功率代入日均所需功率表達式中，可以獲得所需功率與功率因子的關系式為

(15)

式中：ρ20和ρ12分別為20 km，12 km處的大氣密度.

由式(15)可知，在其他參數保持不變的情況下，隨著功率因子的增大，太陽能無人機所需功率將會減小.根據獲能模型可以得到太陽能電池日均可提供的功率，進而可獲得功率因子的限制范圍；而升力系數、阻力系數均會隨著攻角的改變而改變，故又可獲得攻角的取值范圍.低雷諾數翼型更適宜于太陽能無人機的飛行環境，更適合作為太陽能無人機的翼型，如 SD7032，E214，E387，FX63-100 和 FX63-137 等[14].本文選取FX63-100翼型對太陽能無人機的相關參數進行仿真分析，在雷諾數Re=2×105時，FX63-100的升力系數、阻力系數以及功率因子與攻角之間的變化關系如圖4～6所示，其中升力系數與阻力系數通過XFOIL軟件計算得到的.

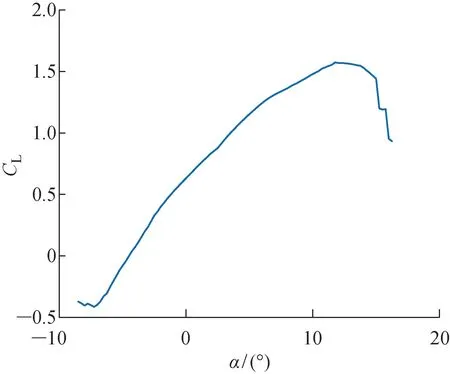
圖4 CL與α之間的關系(Re=2×105)Fig.4 CL versus α (Re=2×105)

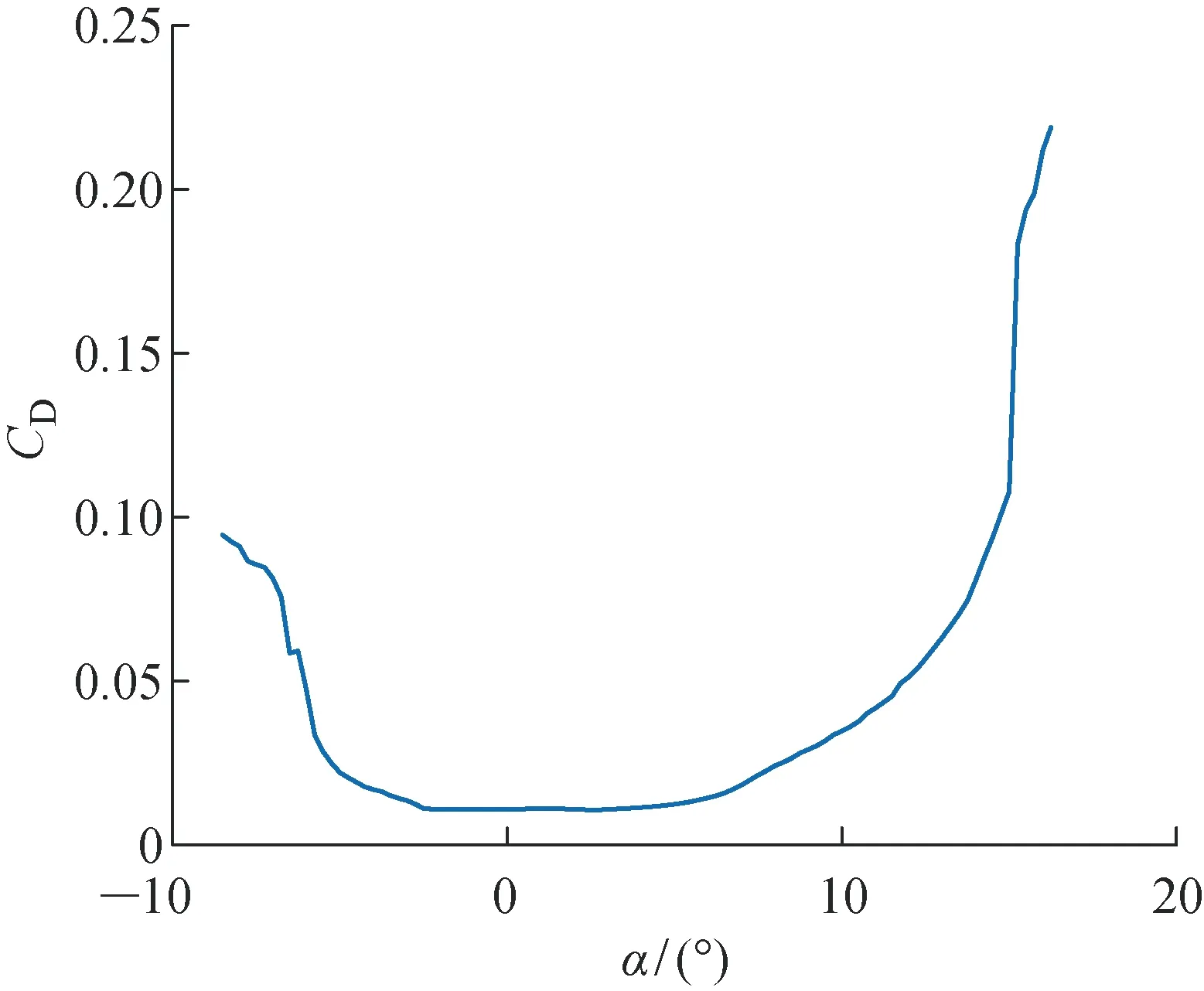
圖5 CD與α之間的關系(Re=2×105)Fig.5 CD versus α (Re=2×105)

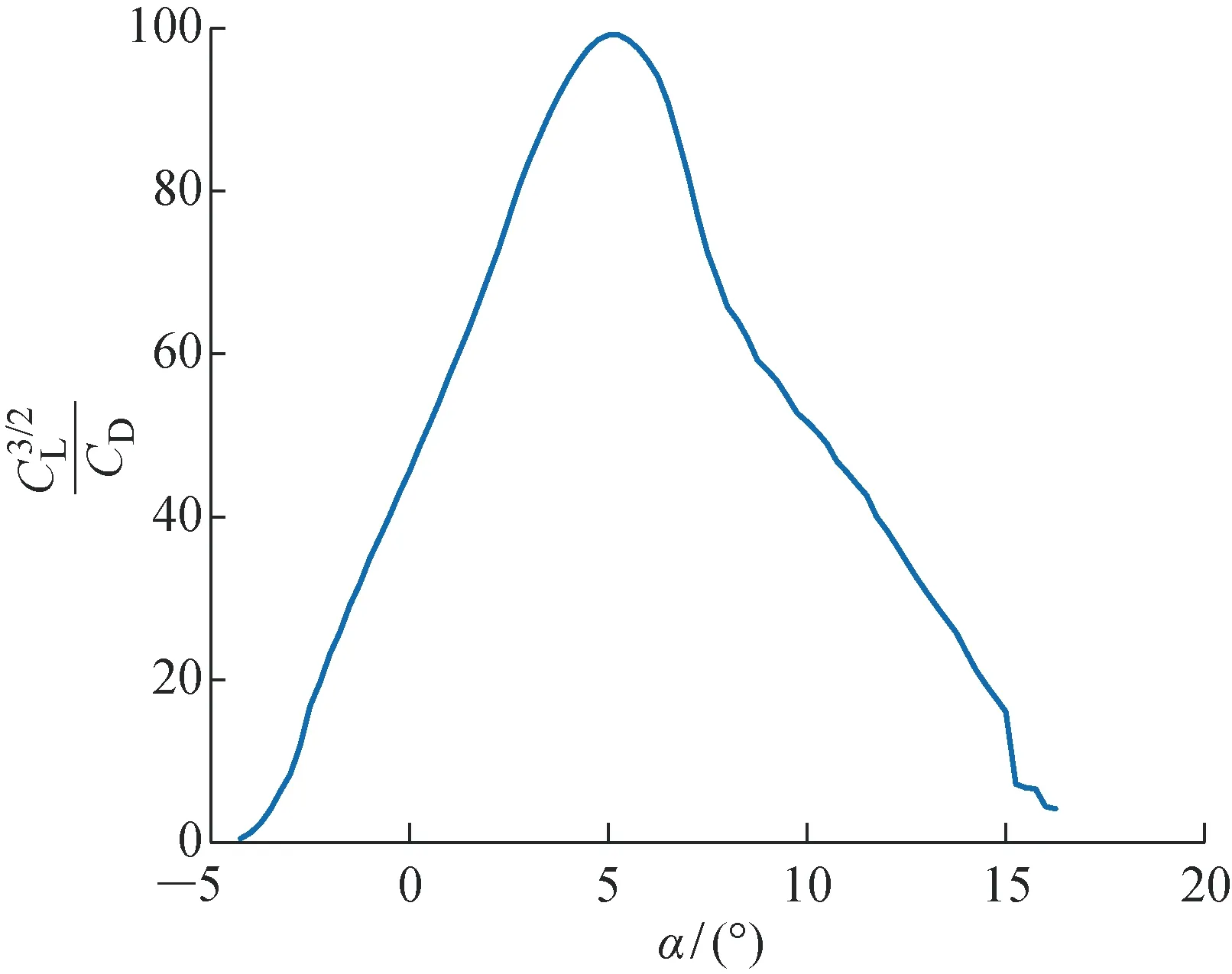
圖6 功率因子與α之間的關系(Re=2×105)Fig.6 Power factor versus α (Re=2×105)

由圖6可知，功率因子在未達到失速攻角(此翼型的失速攻角約為12°)時，隨著攻角的增加先增大后減小，且存在最大值；不同翼型的功率因子隨攻角的變化趨勢大致相同.因此，在確定太陽能電池日均可提供的功率后，可以根據功率因子的大小限定其飛行攻角.

3.2 無人機質量約束

整理日均所需功率表達式可以得到

(m3/2/b)

(16)

式中：等式右側第1項為航電系統與載荷所需功率；第2項為推進系統所需功率，可由Pprop表示，記為

(17)

而太陽能無人機的總質量可以表示為

m=maf+mprop+mbat+msol+

mMPPT+mav+mpld

(18)

式中：maf為結構質量；mprop為推進系統質量；mbat為儲能電池質量；msol太陽能電池質量；mMPPT為MPPT系統質量；mav為航電系統質量；mpld為有效載荷質量.其中，mMPPT、mav及mpld由任務需求確定，不隨其他參數的變化而變化.

無人機結構質量受翼展和展弦比影響，根據經驗公式有

maf=kafARx1bx2

(19)

式中：kaf為結構因子；x1為展弦比因子；x2為展長因子.推進系統質量可以表示為

mprop=kpropPprop=

(20)

式中：kprop為推進系統的質量-功率比.儲能電池質量可以表示為

(21)

式中：kbat為電池能量密度；ηbat為儲能電池的放電效率.太陽能電池質量可以表示為

msol=ksolSsol

(22)

式中：ksol為太陽能電池質量系數；Ssol為太陽能電池板鋪裝面積.

太陽能電池板鋪裝面積需根據日均所需功率和可提供功率間的關系確定，即Pne≤Pprov，此時考慮兩者相等及能量平衡情況，則鋪裝面積可表示為

(23)

為了使上述公式更為直觀簡潔，將式(20)～(22)的推進系統、儲能電池、太陽能電池的質量記為

由式(19)和式(24)～(26)可以看出，太陽能無人機的結構質量主要由翼展和展弦比決定，推進系統、儲能電池、太陽能電池質量都受到翼展、展弦比和總質量三者的約束.無人機總質量可以表示為

a1+a3+mMPPT+mav+mpld=

a7m3/2+a8

(27)

令z=m1/2，則有

(28)

為使方程有正實根，則要求

(29)

(30)

以上是基于無人機所需能量與可提供能量相等分析獲得的.通過上述分析可知，無人機質量與各參數之間的關系，以及各參數的限制范圍，在無人機設計的過程中可以根據式(30)確定不同組合的展長與展弦比是否滿足要求，并且可以通過計算獲得無人機的總質量.

課題組自行設計的參數如表1所示.其中：CDa為翼型阻力系數；CDp為寄生阻力系數；e為Osward系數.參照上述參數對模型進行仿真，可以獲得無人機翼展、展弦比與總質量的關系以及無人機翼展與各分系統質量的關系，如圖7和8所示.

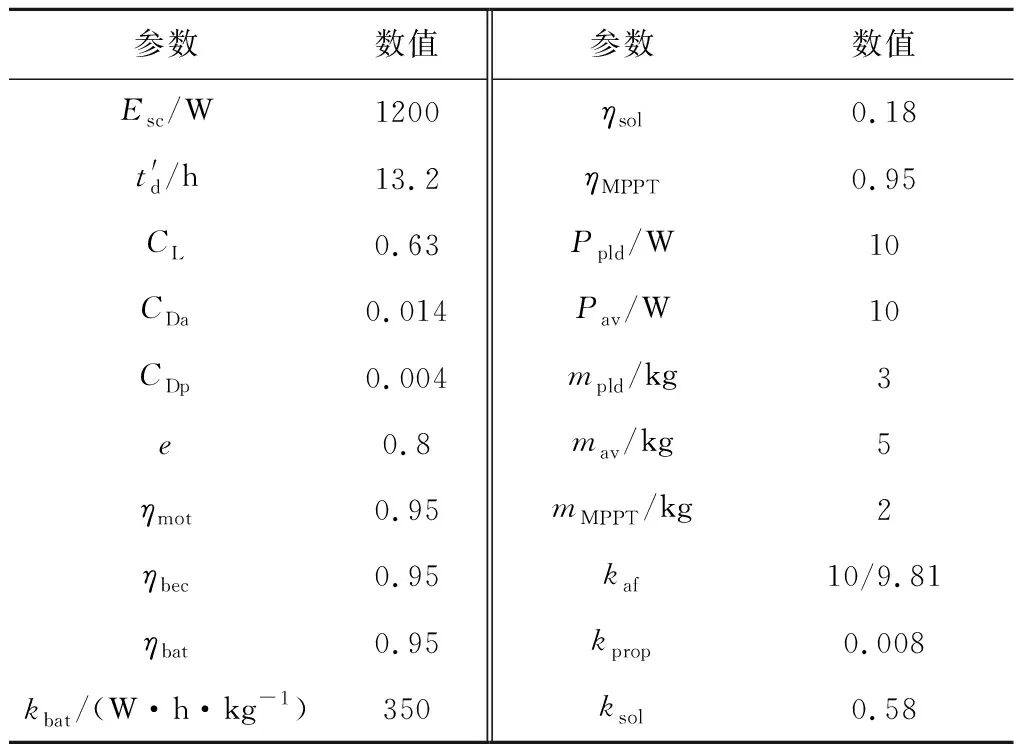
表1 太陽能無人機參數Tab.1 Parameters of solar powered UAV

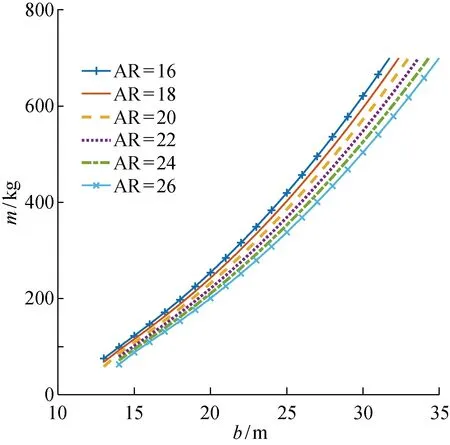
圖7 無人機翼展、展弦比與總質量的關系Fig.7 Wingspan, aspect ratio versus total mass of UAV

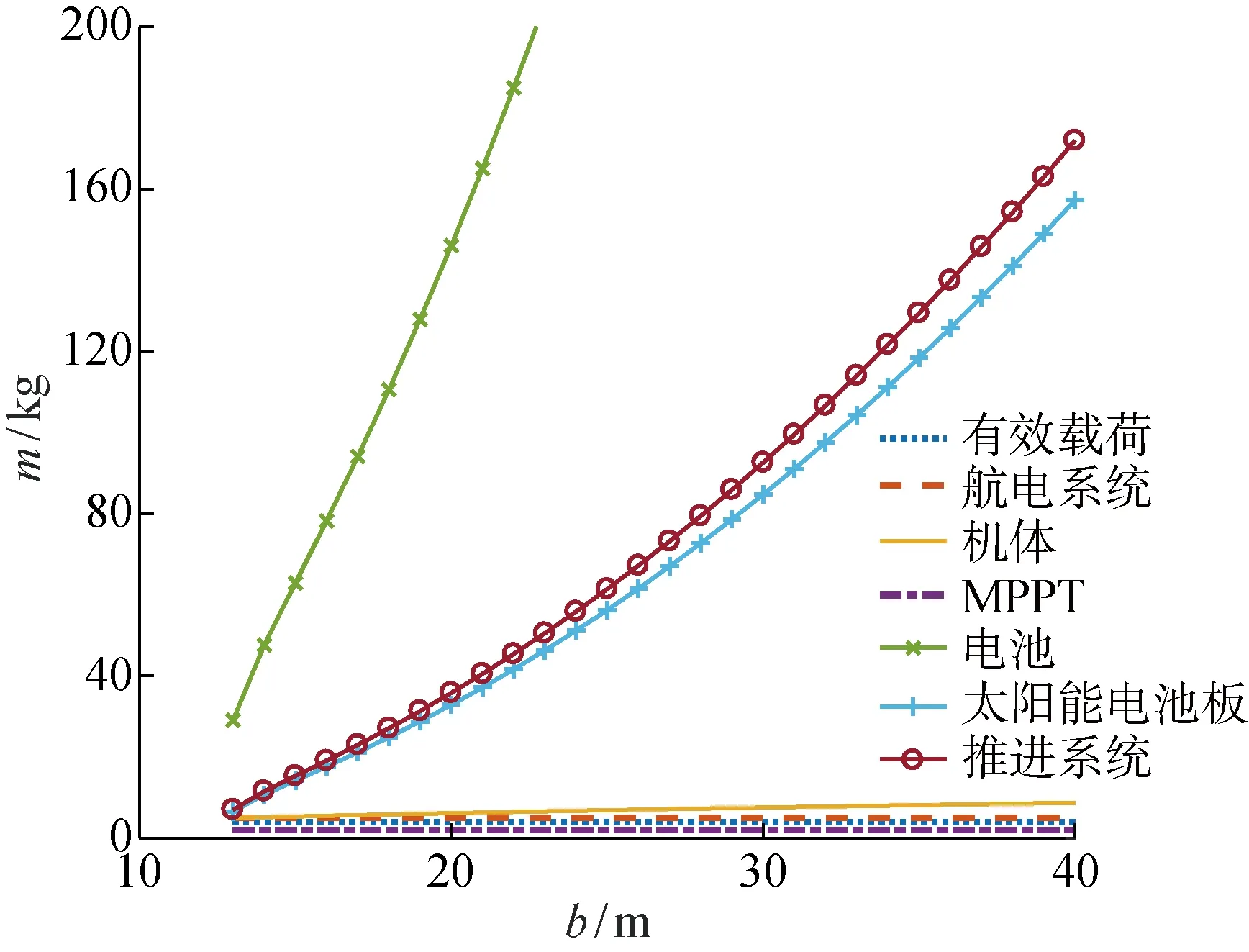
圖8 無人機翼展與各分系統質量的關系Fig.8 Wingspan versus masses of subparts

由圖7可知，隨著翼展的增加，無人機總質量增加；當翼展為定值時，展弦比越大，無人機總質量越小.由圖8可知，儲能電池質量隨著翼展的增大而迅速增加，太陽能電池和推進系統質量也均隨著翼展的增加而增大，這三者質量的增加主要是受到無人機總質量增大的影響，而機體質量則隨著翼展的增大緩慢增加，以上增長趨勢與式(19)，式(24)～(26)相對應.而有效載荷、MPPT、航電系統的質量則根據任務需求預先設定，不隨翼展的變化而變化.

以上為產能和耗能相平衡的情況，下面主要考慮當能量存有余量時，討論太陽能電池質量與儲能電池質量對功率供應的影響.

3.2.1太陽能電池質量影響 對于太陽能電池，其質量表達式可由式(22)改寫為

msol=ksolηpaveS

(31)

式中：ηpave為太陽電池鋪裝率.對于太陽能電池，其鋪裝面積越大，所能產生的能量越多，但質量越大，所需功率也需要相應增大，故需要在機翼面積限制范圍內，找到最佳鋪裝率以獲得最高的能效.當ηpave=0.5～1時，太陽能無人機的所需功率和產能功率對應的變化關系如圖9所示.

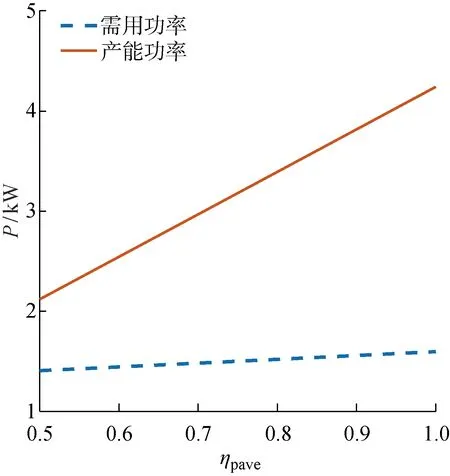
圖9 所需功率、提供功率與鋪裝率的關系Fig.9 Power required, power available versus paving rate

由圖9可知，在滿足能量供應的前提下，ηpave越大，能量剩余越大；當ηpave=1時，即太陽能電池滿鋪裝時，能量剩余量最大.因此，在設計太陽能無人機時，應盡可能多的鋪裝太陽能電池板，有助于更好地滿足飛行需求，實現跨晝夜持續飛行.

3.2.2儲能電池質量影響 白天巡航時，太陽能電池產能部分用于推進、航電和載荷，部分用于為儲能電池充電，電池容量要足夠大以滿足夜間能量的需求.若考慮15%的安全余量，則儲能電池夜間實際可提供的能量為

E=0.85mbatkbatηbat

(32)

儲能電池質量越大，可提供的能量越多，而質量越大，飛行功率也就越大，消耗的能量也越多，只要儲能電池提供的能量恰可以滿足夜間飛行需要即可，太陽能無人機夜間所需功率可以表示為

(33)

令式(33)與式(32)相等即可得到儲能電池的最小質量要求.

3.3 展弦比對能源系統參數的影響

式(16)可以整理為所需功率和展弦比的關系式

(34)

由此關系式可以得到，在其他參數保持不變的情況下，日均所需功率與展弦比的平方根成正比，即隨著展弦比的增大，日均所需功率緩慢增加.

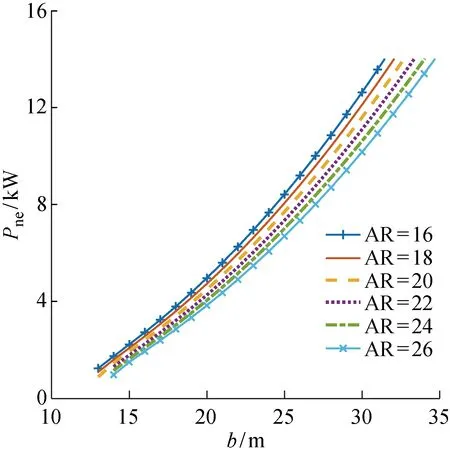
圖10 無人機翼展、展弦比與日均所需功率的關系Fig.10 Wingspan, aspect ratio versus power required

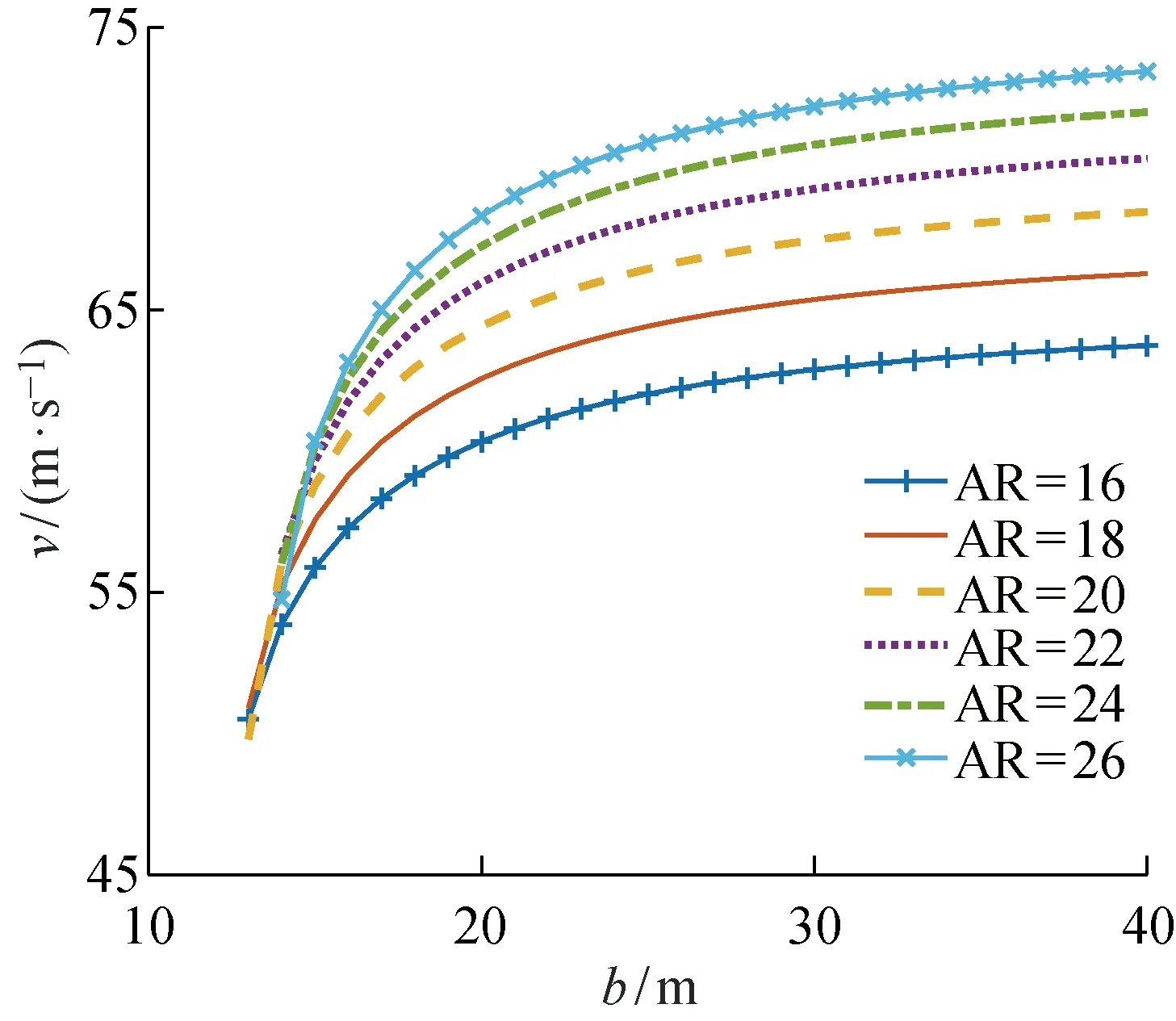
圖11 無人機翼展、展弦比與平飛速度的關系Fig.11 The relationship among wingspan, aspect ratio and velocity for level flight

圖12 無人機翼展、展弦比與翼面積的關系Fig.12 Wingspan, aspect ratio versus wing area

在固定展弦比的情況下，所需功率與翼展長也有一定的關系.結合3.2節中的無人機質量模型，分析不同展弦比的太陽能無人機平飛所需功率、速度、翼面積與翼展的關系，如圖10～12所示.結合圖7和圖10～12可以看出，不同展弦比下無人機總質量與翼展的關系.相同翼展情況下，展弦比越大，無人機總質量就越小，翼面積也越小，平飛速度增加，但平飛所需功率降低；而在同一展弦比下，翼展越大，無人機總質量就越大，翼面積也越大，平飛速度增加，平飛所需功率增大[13].

4 結語

本文從太陽能無人機的典型飛行剖面著手，討論了爬升、白天巡航、下滑以及夜間巡航4個階段的所需功率，并分析整理日均所需功率.根據模型分析得出了功率消耗與功率因子、展弦比、質量之間的關系，同時對相關參數的敏度進行了研究.

分析了功率因子隨攻角的變化規律，獲得滿足能量需求的攻角變化范圍；分析了太陽能無人機各子系統以及整體質量的影響因素，討論了儲能電池和太陽電池質量對功率的影響；分析總結了翼展和展弦比對平飛速度以及所需功率的影響；通過對耗能模型進行參數敏度分析，有利于確定滿足飛行需求的太陽能無人機整體參數，對太陽能無人機總體設計及能源系統的設計具有重要的實際意義.

除了功率因子、展弦比和無人機質量以外，影響太陽能無人機駐空飛行的因素還有儲能電池能量密度、太陽能電池轉化效率、能源系統效率、推進系統效率等，從太陽能無人機的總體設計角度來說，這些因素都是要重點考慮的，也是下一步的研究重點.本文從總體建模仿真的層面，提取了上述3個參數作為分析重點，主要基于現有工程技術水平進行研究，在后續的研究中將繼續擴展參數的分析范圍.