拓寬大涵道比風扇穩定運行范圍的葉片優化設計

張 科， 吳亞東,b

(上海交通大學 a. 機械與動力工程學院； b. 燃氣輪機與民用航空發動機教育部工程研究中心， 上海 200240)

大涵道比風扇作為渦扇發動機的核心部件之一，其性能的改善對于發動機性能的提高有著至關重要的作用，而風扇葉片性能的提升依賴于良好的葉片設計[1].

目前，大涵道比渦扇葉片經歷了從窄弦二維氣動設計向寬弦復合彎掠三維氣動設計發展，設計點性能獲得了較大的提高[2].然而，多數渦扇發動機的風扇葉片加功量沿葉高向上呈增大的趨勢，使得上半葉高的承載量過大而引起氣動、結構的穩定性問題.一方面，葉頂流速過大而出現更大程度的非定常流動，增大了流動損失，減小了流動的穩定裕度；另一方面，葉尖振動較大，易引發顫振、疲勞等結構問題.通過改變葉片設計方法、改變加功量沿徑向的分布規律，將加功量分布重心向葉根方向移動，改善葉頂流動、減小葉尖振動，從而增強風扇葉片的氣動穩定性和結構特性，顯得尤為重要.

葉片設計的理論依據是葉片幾何造型的變化引起其氣動性能參數的規律變化[3].因此，簡單葉片的設計可以依循理論規律來進行.然而，大涵道比風扇葉片形狀復雜，其氣動設計是多目標、多變量設計，需要設計人員有豐富的設計經驗積累.另一方面，基于理論的葉片設計方法存在計算容易發散、設計結果較粗糙等缺陷，難以滿足復雜風扇葉片的設計要求.

隨著計算機技術和流體力學數值計算技術的發展，將數值優化技術與正向流場計算相結合的葉型自動優化設計技術日益受到關注[4].自動優化設計技術的實質是在由設計參數構成的向量空間中，采用優化控制理論求出整個可行域的目標函數極值.一方面，設計過程由數值優化替代設計人員經驗，控制設計參數修改方向，更加嚴密、客觀、有效，并可以實現多變量、多工況組合設計.另一方面，對自動優化設計結果的分析可用于指導葉片的理論設計.

自1983年Sanger[5]首次采用數值最優化方法對控制葉型氣動性能進行優化設計以來，風扇優化設計方法得到了快速發展.Adeeb等[6]、Oyama等[7]及Trepanier等[8]都基于多種優化算法，針對不同的優化目標對葉片進行優化，旨在提升葉片性能，收效甚好.

近年來，國內也逐步構建了從通流設計到三維葉片設計的完整葉輪機械氣動優化設計體系，并取得了良好的效果.脫偉等[9]基于遺傳算法，以最大化總壓比和絕熱效率為目標，對5級高壓壓氣機進行了S2流面二維氣動優化，使得壓氣機性能明顯提升.孫俊峰等[10]結合利用基于進化算法的多目標優化方法、多目標優化設計Pareto解的思想和約束處理機制，建立了旋翼翼型的優化設計系統.張金環等[11]基于局域網的并行遺傳算法優化平臺，實現了對大涵道比風扇的多幾何參數的組合優化設計.

在利用改變徑向負荷分布的方法改善葉片氣動性能方面，高星等[12]對高比轉速斜流葉輪根尖加功量分配的影響分析研究表明，強根部設計利于改善葉輪出口流場的均勻性、有利于獲得更高的效率、有利于獲得較高的失速壓比.

本文以大涵道比渦扇發動機風扇葉片為原型，取不同葉高截面處葉型安裝角的扭轉角度和最大厚度相對位置實現參數化表達，以此作為自動優化的設計變量，選取可以衡量風扇葉片穩定運行范圍的目標函數，代入Kriging模型中進行拓寬穩定運行范圍的自動優化，得到最優結果并分析驗證其氣動特性.

1 研究對象介紹

采用ANSYS TurboGrid 和ANSYS CFX 進行網格自動生成和計算流體力學(CFD)仿真計算.網格劃分過程中，設置葉頂間隙為2 mm，單流道網格數為70 萬，并經過網格無關性驗證.優化進程中，湍流模型采用k-ε模型，流體為理想空氣，進口邊界設置為總壓入口，出口邊界條件設置為流量出口，壁面采用絕熱光滑無滑移邊界條件，收斂殘差設定為均方根(RMS)小于10-5.綜合權衡優化效率和計算精度，采用穩態仿真進行CFD計算.用于CFD計算的大涵道比風扇幾何造型圖如圖1所示.

圖1 用于CFD計算的大涵道比風扇幾何造型圖Fig.1 Geometry of high bypass ratio fan used for CFD calculation

葉片設計最好能用較少的設計參數確定出定性合理、可變性較大的葉片造型，設計參數越多，葉片造型可變性越大，但優化計算工作量也越大.同時，不同葉片造型設計參數選取還影響最優解的搜索效率，即達到最優解所需的迭代步數，不同葉片造型修改函數影響優化設計的收斂性和最終設計結果的質量.

風扇葉片的原型為大涵道比渦扇發動機風扇葉片，通過導入葉型、機匣及輪轂的型線文件，在 ANSYS TurboGrid中完成對單級風扇轉子葉片的建模與網格劃分.

由于對葉片的積疊線不做改動，三維葉片的參數化問題可以簡化為準三維參數化問題，即對不同葉高處的葉型進行基于疊加修改量的葉型重構，從而實現葉型修改.

對葉型的具體修改包括葉型扭轉和最大厚度相對位置的移動.圖2是葉型安裝角扭轉示意圖，圖中α為葉型的旋轉角度.葉型扭轉基于每個平面葉型的形心(根據組合圖形的形心公式求得)，對葉型進行一定角度的旋轉操作，l為該徑向位置處的葉型弦長.圖3是葉型最大厚度相對位置變化示意圖.最大厚度相對位置的移動基于葉型的中弧線和內切圓，中間為原葉型對應的最大厚度相對位置，上、下分別為將此位置左移和右移.改變最大厚度所在位置附近一定范圍內的內切圓半徑分布，以此實現最大厚度相對位置的改變.

圖4是葉型重構流程圖，圖中x為葉型的弦長方向坐標，y為厚度方向坐標.由原型葉片的點系，依次經過樣條擬合，由上、下型線確定中弧線與內切圓，固定中弧線、改變最大厚度位置并扭轉，得以重構葉型并取點，形成改型葉片的點系，進而進行CFD計算.

各徑向位置處葉型的安裝角扭轉角度α1～α7和最大厚度相對位置d1～d7的變化范圍如表1所示.其中n為徑向位置編號，1～7對應葉根到葉尖方向，l為該徑向位置處的葉型弦長.對于安裝角扭轉角度而言，“+”表示按順時針方向旋轉，“-”表示按逆時針方向旋轉.d為最大厚度相對位置，“+”表示向葉型前緣方向移動，“-”表示向葉型尾緣方向移動.

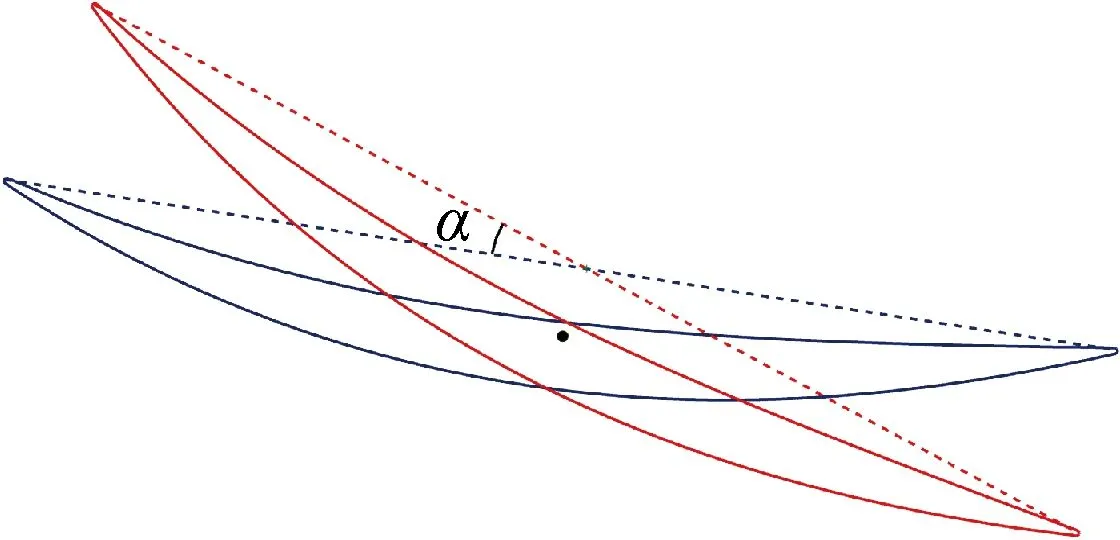
圖2 葉型安裝角扭轉示意圖Fig.2 Sketch of setting angle rotating of airfoil

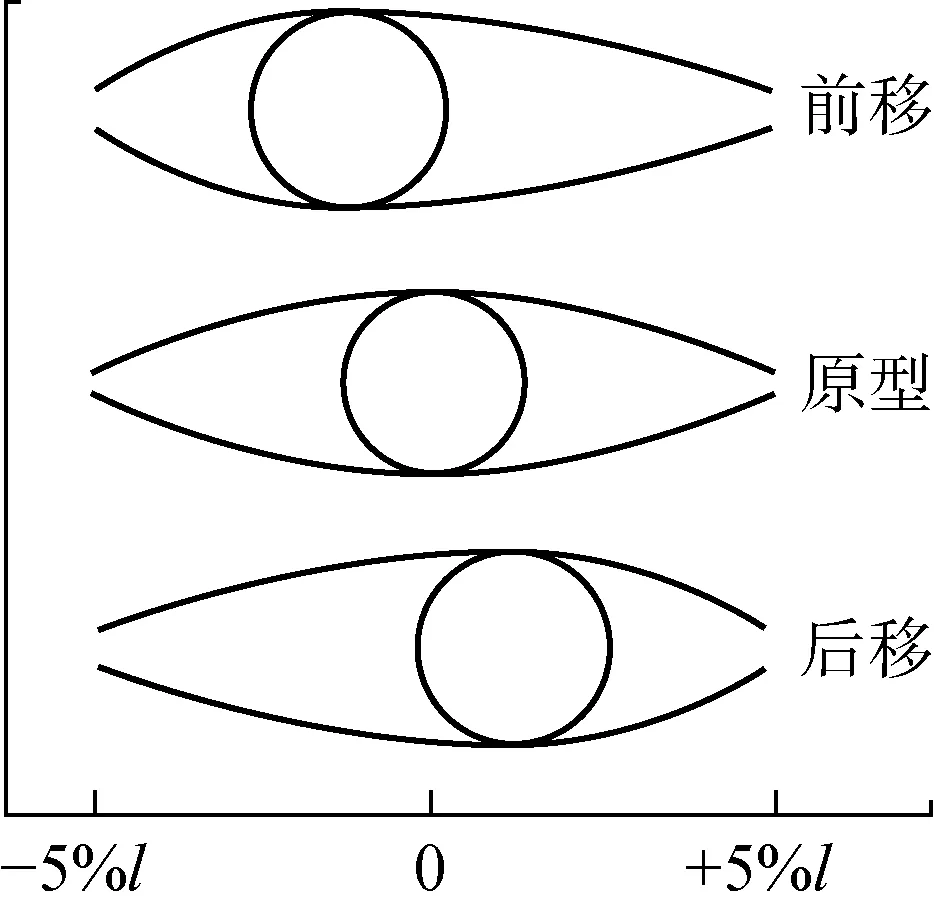
圖3 葉型最大厚度相對位置變化示意圖Fig.3 Sketch of maximum-thickness relative position moving of airfoil

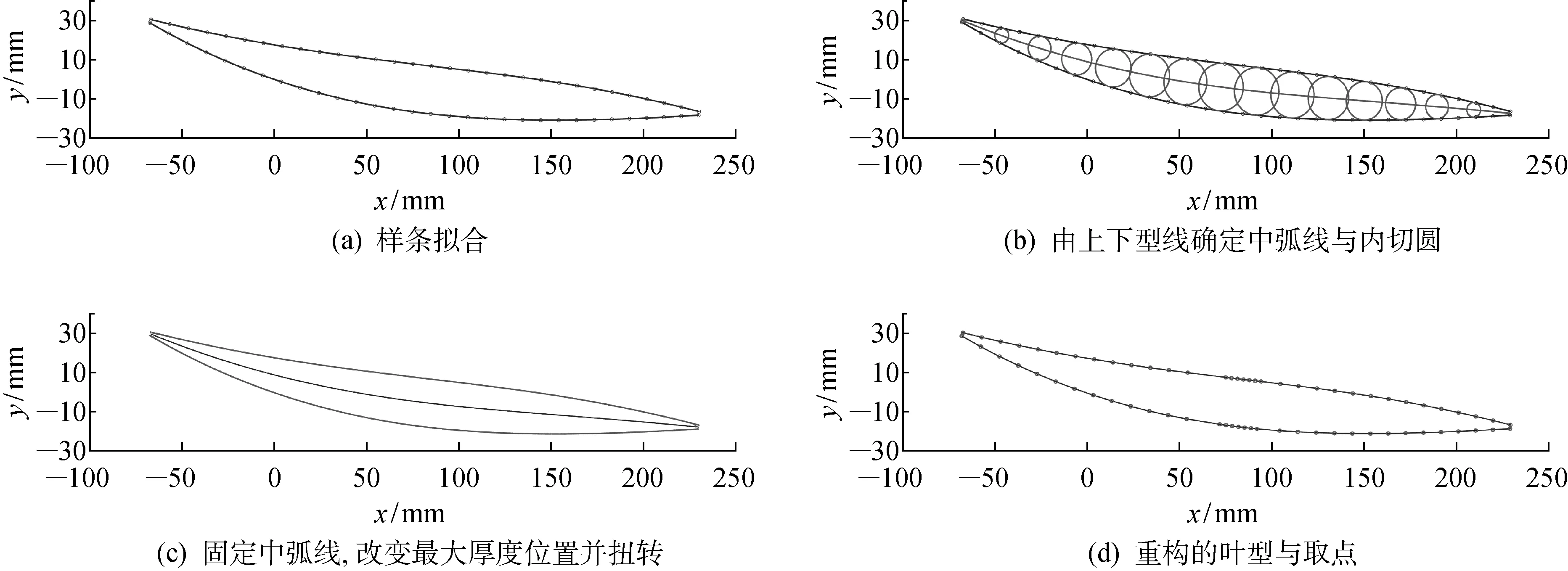
圖4 葉型重構流程圖Fig.4 Flow chart of airfoil redesign

表1 葉型扭轉角度和最大厚度相對位置變化范圍Tab.1 Span of angle rotating and maximum-thickness relative position moving of airfoils

通過上述兩種方式，對不同葉高處的葉型進行了不同程度的修改，從而改變氣流參數和加功量沿徑向的分布，實現葉片的優化設計.

2 優化方法及設計

2.1 Kriging代理模型

基于遺傳算法的多目標優化方法在優化迭代的過程中需要進行大量的目標函數和約束函數的求解，若追求高精度的CFD計算，將耗費巨大的計算機資源和時間成本.一種有效的替代方式是建立復雜CFD性能分析的近似模型，本文采用Kriging代理模型作為高精度CFD性能分析的近似模型.Kriging模型是從地理統計學科發展起來的一種插值函數模型，使用高斯隨機函數插值采樣點來估計隨機過程的趨勢.由于Kriging模型可以精確擬合氣動設計中的非線性、多峰特性等復雜問題，并能實現高效尋優、減少計算成本，所以在氣動設計領域獲得了廣泛的應用[9-10].

Kriging模型可以表示為

y=μ+z(x)

(1)

式中：x為m維的設計變量；μ為全局常數；y為響應值；z(x)是均值為0，方差為σ2的隨機過程.z(x)的協方差矩陣為

cov[z(xi),z(xj)]=σ2R[R(xi,xj)]

(2)

式中：R為相關矩陣，由所有已知樣本點之間的相關函數值組成，

R(xi,xj)為任意兩個采樣點xi和xj的高斯相關函數，定義為

(3)

θ(θk>0)為未知的相關參數權因子，下標k表示采樣點設計變量矢量的分量，該函數控制最終模型的光滑性.相關參數θ(θk)由最大化似然函數決定：

(4)

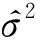
建立初始代理模型后，需要通過一定的“優化加點準則”循環產生新的樣本點，直到優化收斂.本文采用韓忠華[13]介紹的EI(Expected Improvement，即改善期望)準則進行采樣點的更新，期望E的計算公式為

E[I(x)]=

(5)

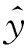
對于多設計變量的優化問題，優化設計過程中存在試驗次數和試驗因素的搭配問題，必須選擇合適的試驗設計方法.均勻設計由方開泰等[14]提出，作為1種科學的安排和分析試驗的方法，可以合理安排試驗、減少試驗次數并找出較好的試驗方案，目前已在工業領域獲得廣泛應用.本文采用均勻設計的方法選取采樣點.

在優化設計過程中，利用均勻設計建立初始的樣本空間，在此基礎上建立初始的Kriging代理模型，利用代理模型計算目標函數值，并預測最優解對應的設計變量組合.每隔一定的優化代數計算種群個體EI值，選取EI最大值的點作為新的采樣點重新建立Kriging模型，逐步迭代改進提高模型的精度直到優化的結束.

2.2 優化系統的開發與集成

實現氣動優化設計的關鍵是三維參數化模型、網格生成器TurboGrid、CFD求解器CFX-Solver和基于Kriging代理模型的優化算法之間的數據集成和過程集成.數據集成完成了各個軟件之間數據的靜態傳遞，而氣動優化過程是一個反復迭代尋優的過程，在氣動優化設計中需要將各個模塊過程集成，并且要盡量避免對優化過程的人工干預，以加快尋優速度和減小尋優過程的出錯概率.

通過MATLAB的葉型參數化函數進行葉型的修改，生成重構葉型的點狀文件傳遞給ANSYS TurboGrid軟件，TurboGrid利用腳本文件批處理實現幾何生成和網格自動劃分并輸出.然后通過ANSYS CFX的CCL語言讀取網格自動完成邊界條件加載并計算.繼而采用CFD-POST的后處理功能自動提取結果文件的數據并將分析結果輸出.分析結果作為新的樣本點加入到Kriging代理模型的樣本庫中進行擬合并尋優，預測到最優解，該最優解將作為最新的樣本返回經過新一輪的參數化建模、網格劃分、CFD 計算等步驟，如此反復迭代直至結果收斂.整個系統的運行流程和數據集成過程如圖5所示.

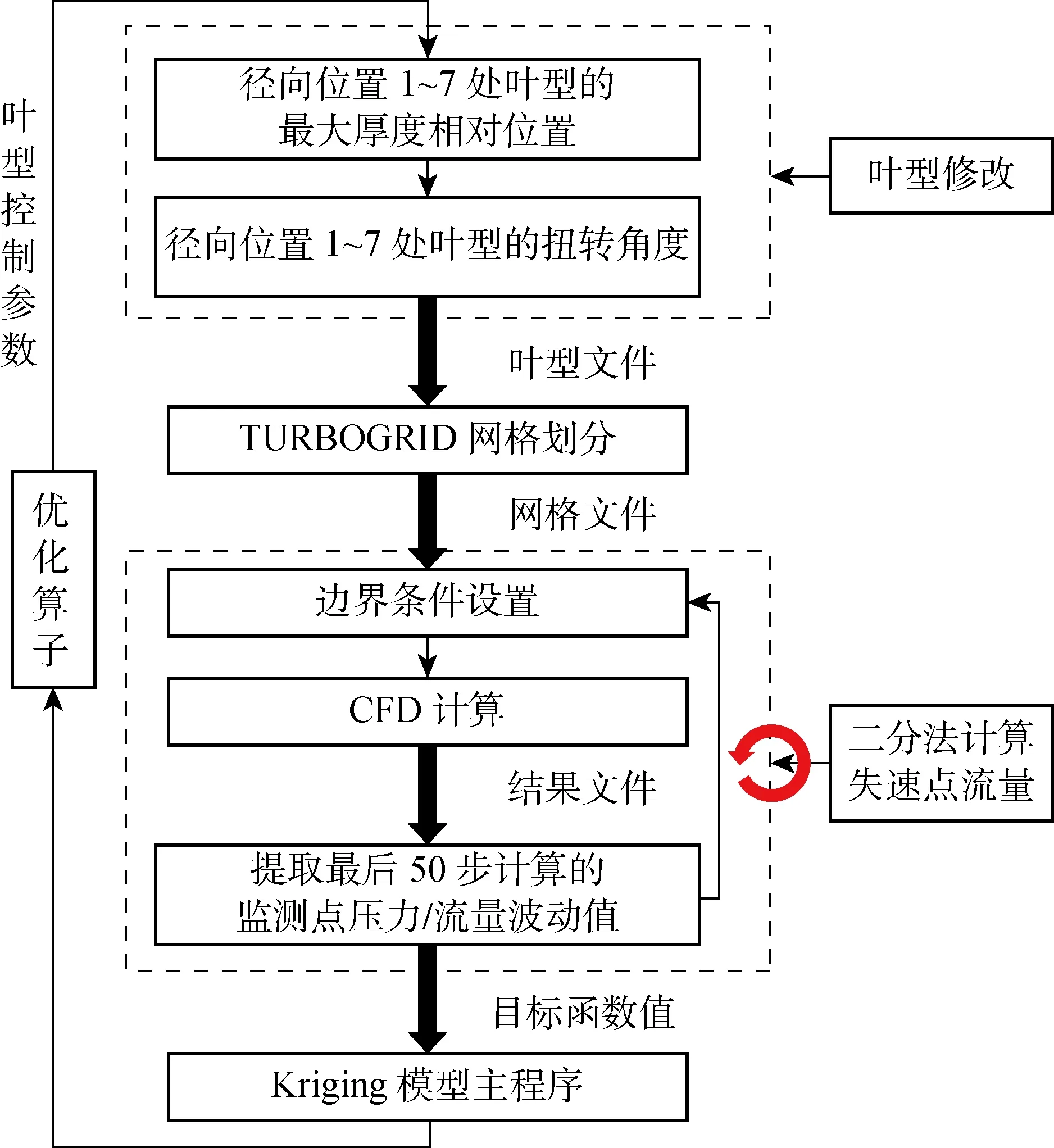
圖5 優化系統集成流程圖Fig.5 Flowchart of integrated optimization system

2.3 目標函數

本文優化是對現有大涵道比風扇進行改進設計，優化目標是拓寬風扇轉子穩定運行范圍，保證其結構特性，并兼顧效率、總壓比.為此，構造目標函數為失速點流量，尋求目標函數最小值.

在CFD仿真計算中，將收斂殘差小于某設定值且流量收斂曲線無波動或者波動幅度小于某設定值認為計算收斂，穩定運行.若收斂殘差大于設定值或流量曲線波動幅度大于設定值則認為其計算未收斂，不在穩定運行范圍內.

在MATLAB優化平臺中，利用批處理功能提取流量收斂曲線的最后50次迭代，計算最后收斂過程中流量的波動值：

(6)

式中：τ為迭代步數；maxmτ，minmτ，avemτ依次為最后50次迭代流量的最大值、最小值和平均值.根據仿真過程的經驗，為此波動值設置一臨界值，若某次計算的流量波動值小于此臨界值，認為在合理范圍內，計算收斂；大于此值則認為流量波動過大，計算未收斂.

3 優化結果分析

3.1 優化結果

圖6為失速點的流量系數隨優化迭代步數的變化示意圖.其中φ為作為目標函數的失速點流量系數.說明經過近60次循環調用CFD優化程序，風扇的失速點流量系數不再有大的變化.

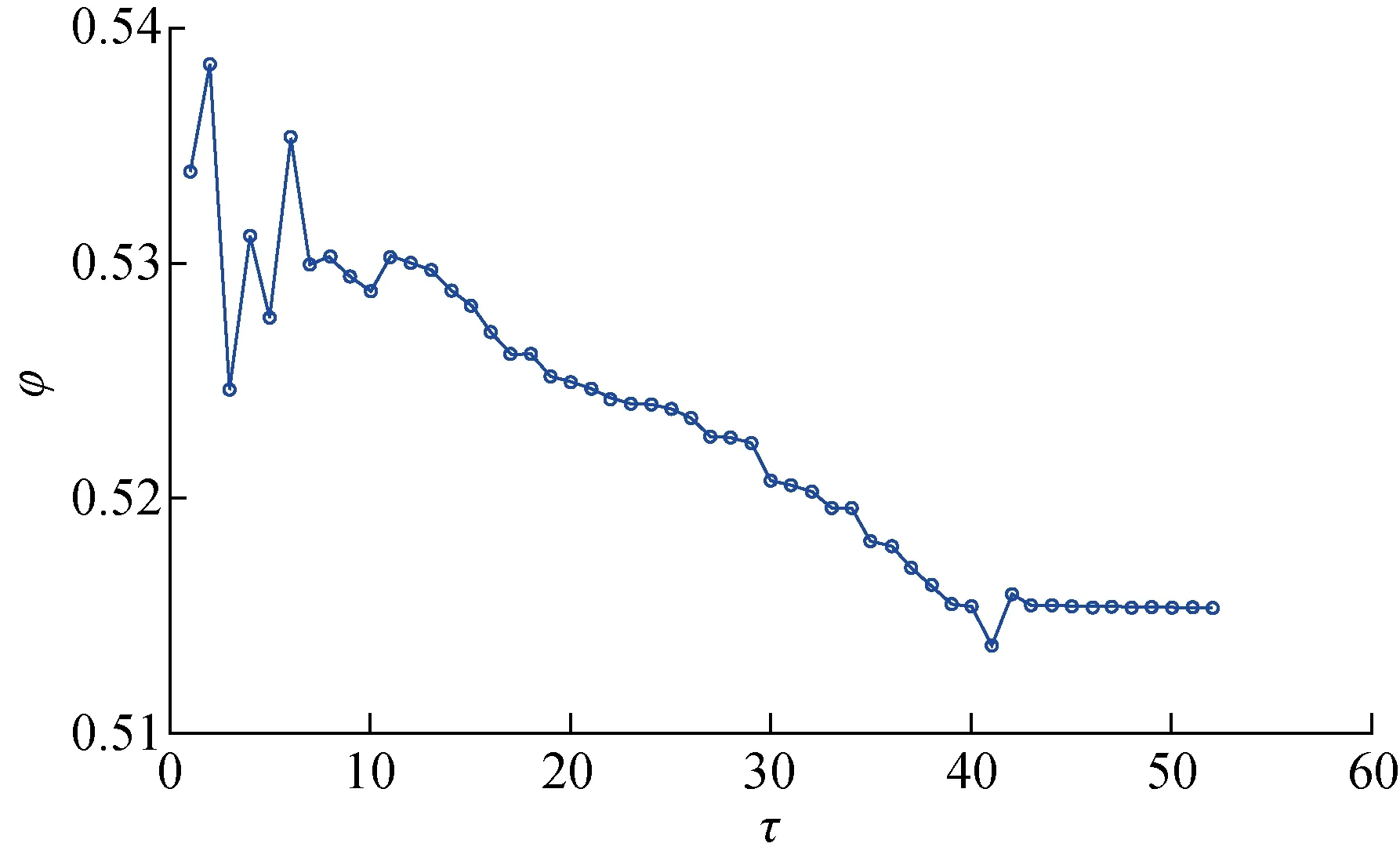
圖6 目標函數值隨迭代步數變化示意圖Fig.6 Sketch of changing object function value with iteration steps

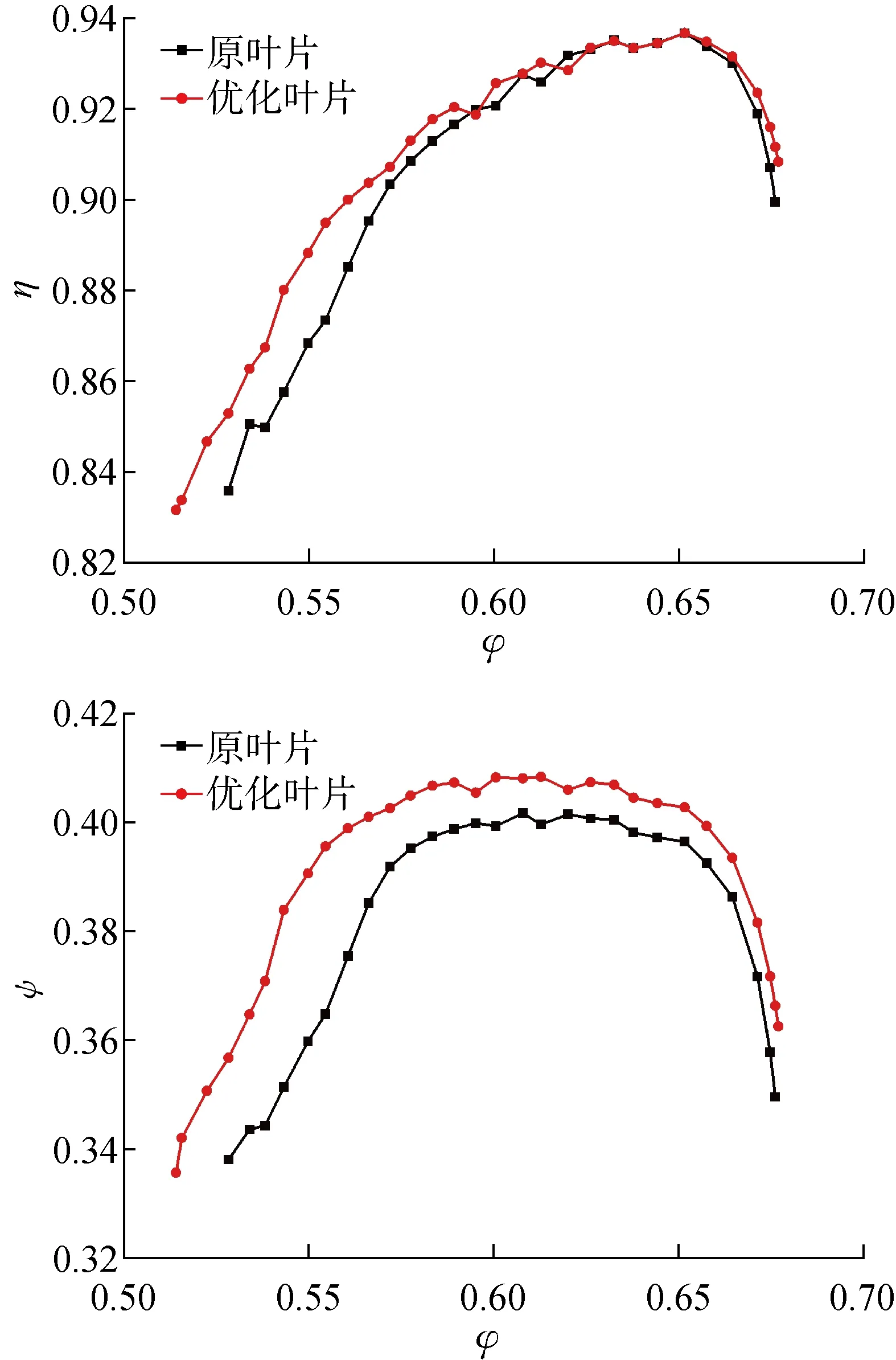
圖7 優化葉片與原葉片的特性曲線對比Fig.7 Comparison of characteristic of original and optimized blades

圖7為優化葉片與原葉片的效率-流量系數、壓力系數-流量系數特性曲線對比圖.其中φ為大風扇的流量系數，η、ψ分別為其效率和壓力系數.通過對比圖可以看出，優化后的風扇葉片的穩定運行范圍(以流量系數表示的范圍)由原來的0.148增加到0.163，增幅為10.1%，穩定運行范圍得以大幅度拓展.而且在穩定運行范圍中，優化葉片表現出較原葉片更高的性能：優化葉片的效率在小流量范圍內有明顯提升，最大增幅為2.63%，大流量范圍內也有所提升；優化葉片的壓力系數在整個穩定運行范圍都有大幅提升，尤其在較小流量范圍內，最大增幅可以達到9.27%.

圖8所示為優化葉片與原葉片在設計工況下的葉片出口總壓徑向分布曲線對比圖.其中：縱坐標為大風扇葉片的徑向相對位置，橫坐標為相應徑向位置處的大風扇出口總壓pt(周向平均值).可以看到，優化葉片的出口總壓在主要做功區域分布更為均勻，葉片加功量的徑向分布有向葉根方向移動的趨勢.

3.2 優化前后葉片形狀對比

圖9為優化前后的葉片三維形狀對比圖.圖10為優化前后葉片在徑向位置1～7處的葉型變化對比圖.其中x′為弦長方向的相對坐標值，y′為厚度方向的相對坐標值(使用相對坐標值以方便進行對比).可以看到，徑向位置6處的葉型變化較小，其他葉高處的截面較原葉型沿逆時針方向都有一定程度的扭轉.具體表現為，優化所得風扇葉片的7個徑向位置處的葉型相較原葉型依次扭轉0.555°、0.555°、0.466°、0.480°、0.604°、0.056° 及0.622°，最大厚度位置改變量依次為 +0.643l%、-3.80l%、+2.91l%、-2.00l%、 +1.84l%、 +1.87l%及+2.17l%.

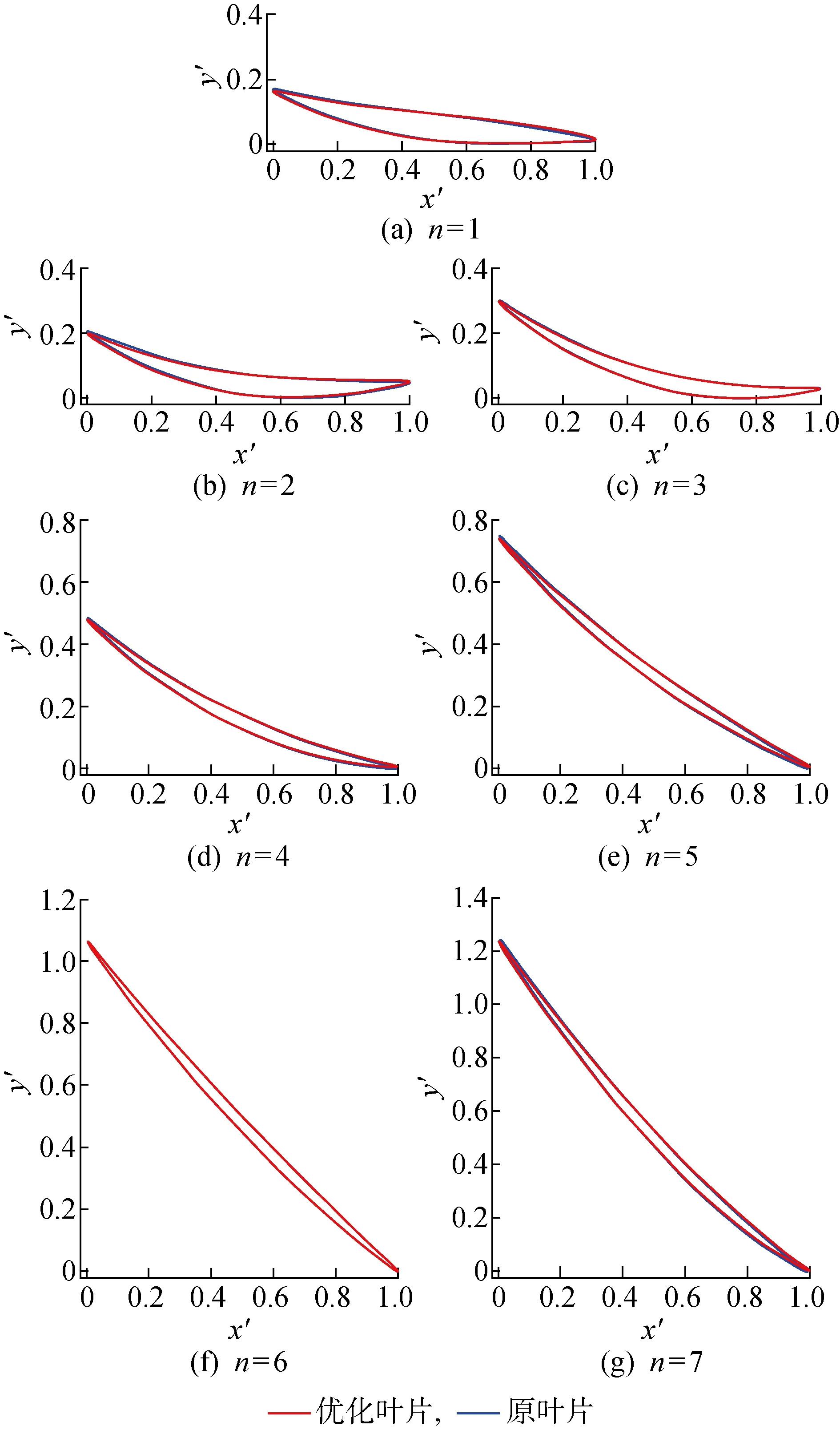
圖10 優化葉片與原葉片在徑向位置1～7處的葉型對比圖Fig.10 Comparison of airfoils of original and optimized blades at span 1—7

3.3 優化前后氣動性能對比與流場分析

圖11、12分別為優化前后葉片在設計工況下和近失速工況下的近吸力面極限流線對比圖，其中v為速度值.可以看出，在設計工況和近失速工況下，優化后的葉片流線分布情況均明顯改善，分離區域變小.尤其是在近失速工況下，原葉片吸力面的渦流區被破壞，分離區域的面積大大減小，速度分布合理的區域變大.

圖13為優化前后葉片根中尖部截面的馬赫數云圖.其中Ma為相對馬赫數，從下至上依次對應20%、50%和80%葉高處的馬赫數云圖.圖14為優化前后葉片根中尖部截面的靜壓p的軸向分布曲線圖.其中橫坐標為軸向相對位置，縱坐標為靜壓，從左至右依次對應20%、50%和80%葉高處的靜壓軸向分布.從葉片尖部截面的馬赫數分布云圖和靜壓軸向分布曲線中壓力陡升的位置均可以直觀地看到，相對于原葉片，優化葉片的激波強度增大，激波在葉片上的作用點后移，表明此時更遠離失速情況；同時尾跡區域由寬長變得狹小，尾跡損失大大減小.與葉尖截面相似，葉片中部和根部截面的尾跡區域同樣由寬長變得狹小，尾跡損失減小.通過對比優化前后葉片各截面處的靜壓分布的曲線走勢，可以看到優化葉片靜壓的沿軸向分布更為均勻，壓升系數在各葉高處均有不同程度的升高，說明葉片的整體增壓能力有較大的提高.

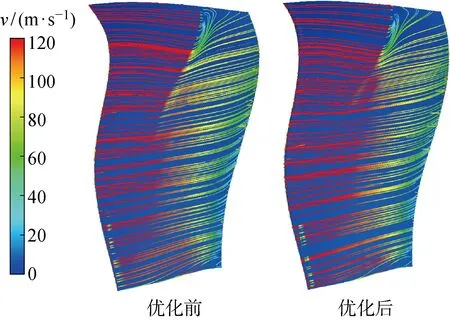
圖11 設計工況下的近吸力面極限流線圖Fig.11 Charts of limited streamline near suction surface under design condition

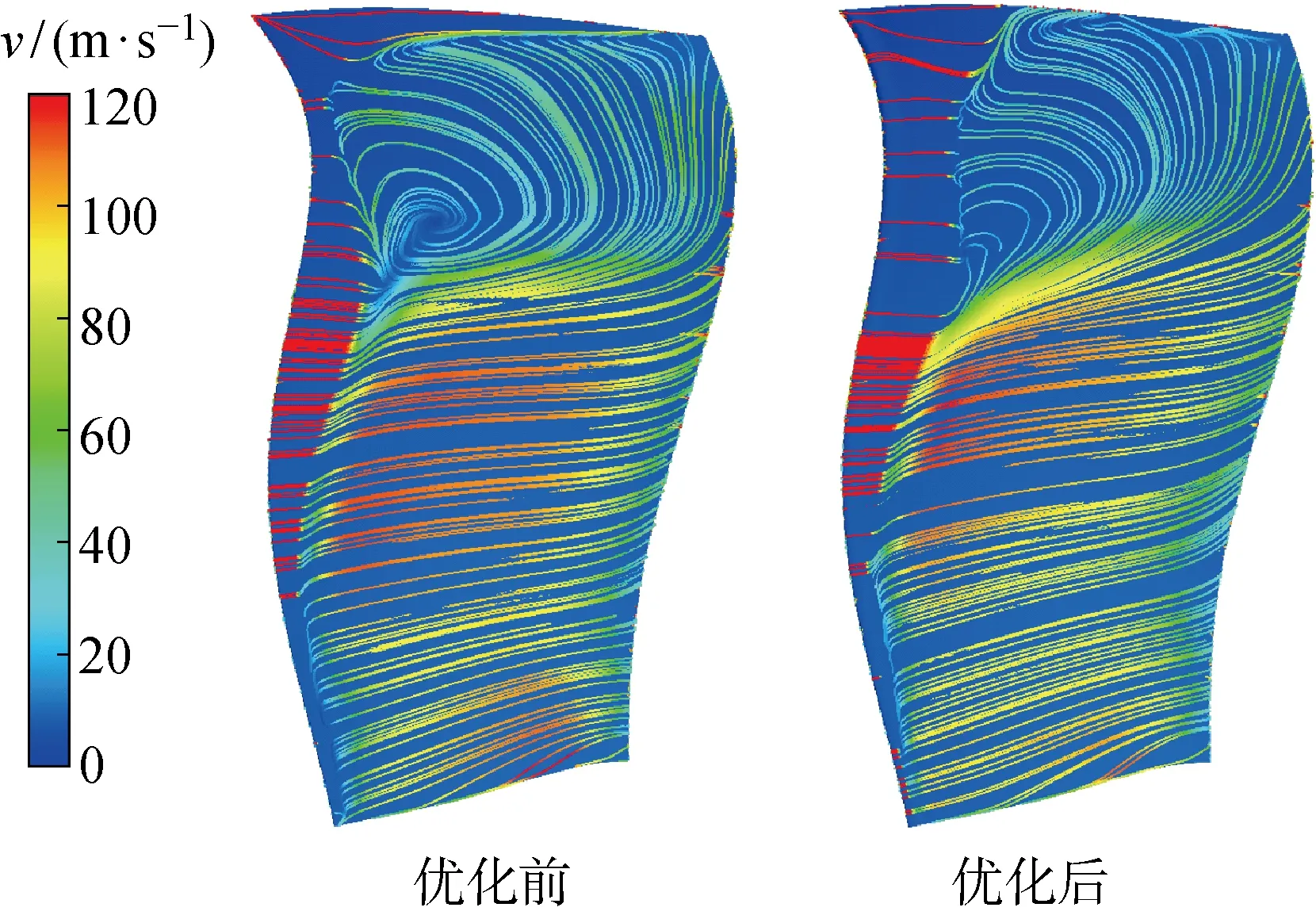
圖12 近失速工況的近吸力面極限流線圖Fig.12 Charts of limited streamline near suction surface under near stall condition

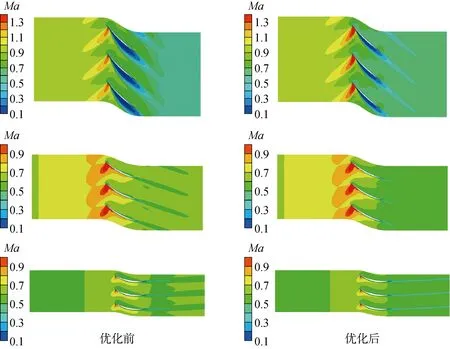
圖13 20%、50%、80%葉高處的馬赫數分布云圖Fig.13 Mach number contours at 20%, 50%, and 80% spans

圖15為優化前后葉片尖部截面的速度矢量圖，圖中v′為相對速度值.可以看到，優化后的葉片尖部截面速度線的指向更趨于相同， 流線分布情況明顯改善，分離區域變小，從而使葉片性能得以提升.

圖16為在設計工況下，優化前后葉片的出口總壓云圖.在設計工況下，總壓高的區域變大，中上部葉高做功能力顯著提升.圖17為近失速工況下優化前后葉片的出口總壓云圖.在近失速工況下，尾跡區域、低速流體區域減小，損失下降.

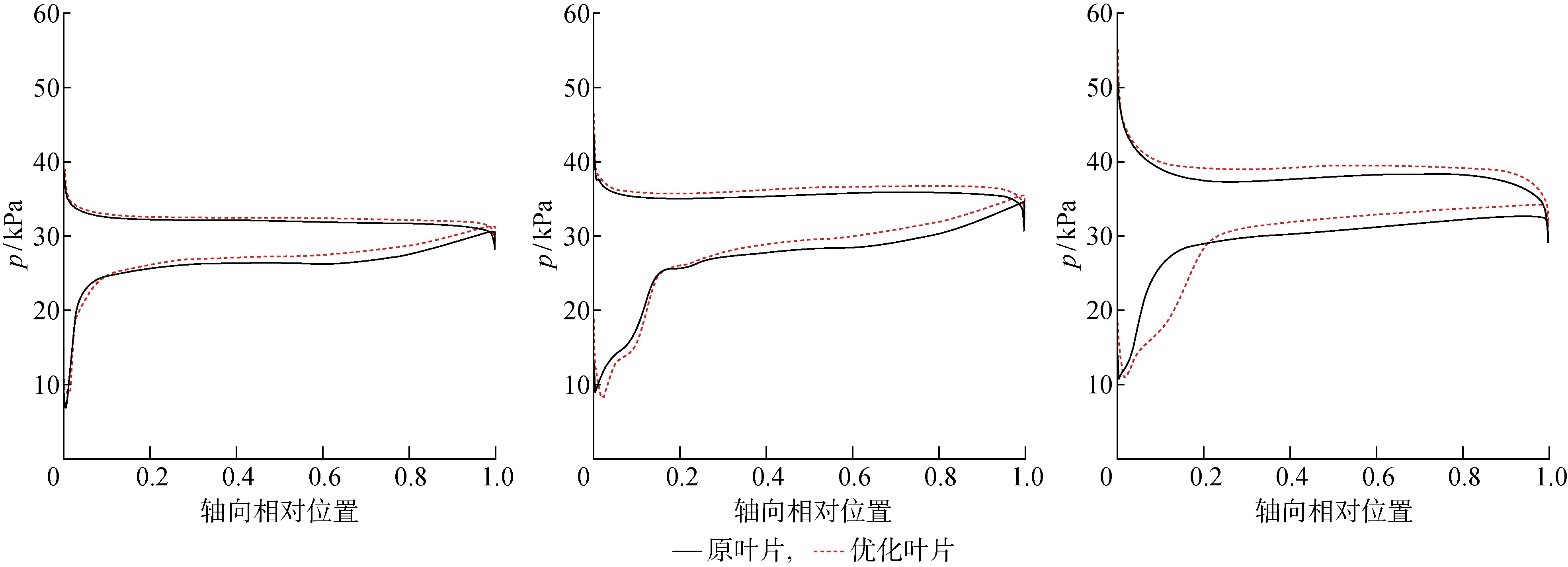
圖14 20%、50%、80%葉高處的靜壓軸向分布曲線Fig.14 Axial distribution of static pressure at 20%, 50%, and 80% spans

圖15 葉片尖部截面速度矢量圖Fig.15 Velocity vector charts of blade tip cross section

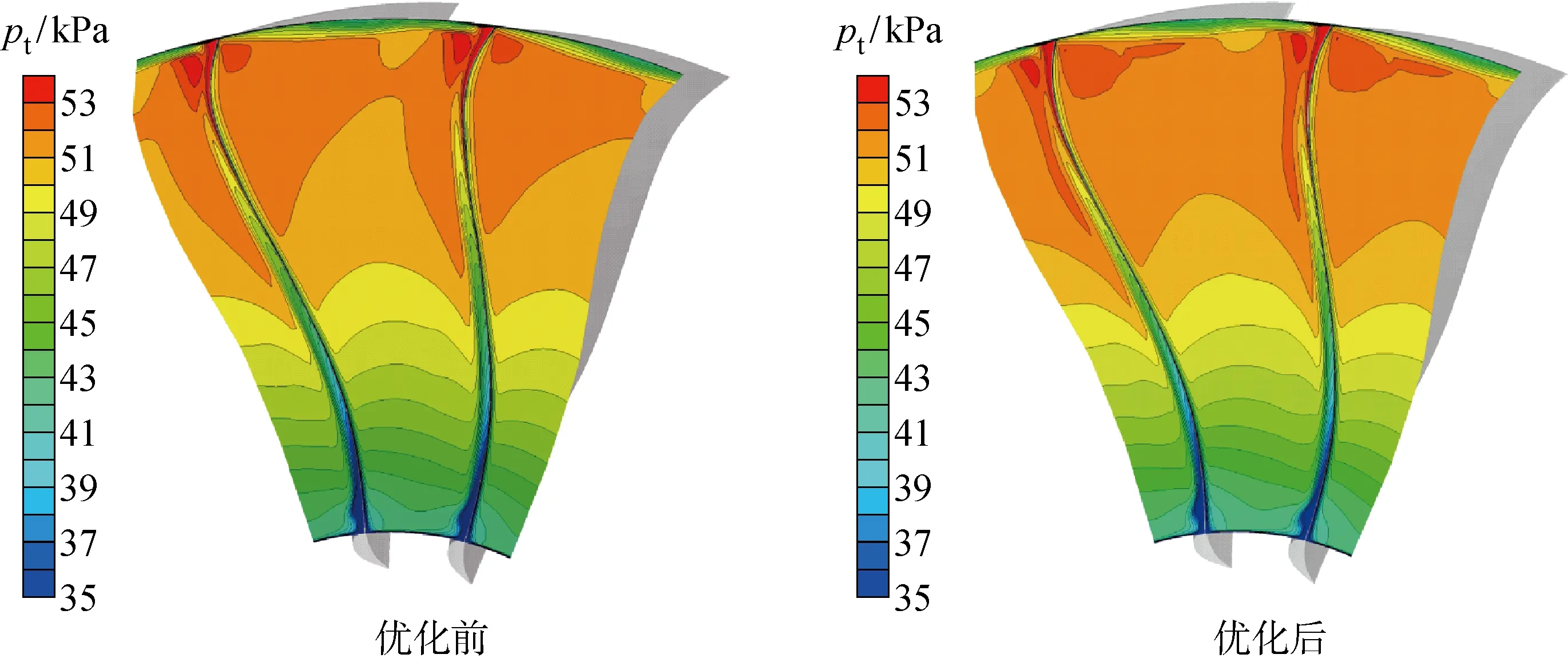
圖16 設計工況下的出口總壓分布云圖Fig.16 Total pressure contours at outlet under design condition

圖17 近失速工況下的出口總壓分布云圖Fig.17 Total pressure contours at outlet under near stall condition

3.4 敏感度分析

為了探究葉型安裝角扭轉和最大厚度位置移動各自對葉片性能的提升效果，提取優化葉片的安裝角扭轉參數和最大厚度位置移動參數，分別作用于原葉片，得到僅安裝角扭轉型優化葉片和僅最大厚度位置移動型優化葉片，通過CFD計算得到特性曲線，與優化葉片、原葉片特性對比.圖18為原葉片、優化葉片、僅安裝角扭轉型優化葉片和僅最大厚度位置移動型優化葉片的特性曲線對比圖.可以看到，將角度扭轉因素和厚度位置因素分離得到的葉片性能基本處于優化葉片和原葉片之間.

進一步分析優化葉片和因素分離所得葉片相對于原葉片性能提升的幅度，圖19為僅安裝角扭轉型優化和僅最大厚度位置移動型優化葉片相對原葉片的性能提升幅度值之和與優化葉片的提升幅度值對比圖，圖中Δη為效率增幅，Δψ為壓力系數增幅.可以看到，兩者隨流量系數變化的趨勢基本吻合，表明優化葉片對原葉片的性能提升可歸結為兩個因素對性能提升的疊加效果.經過計算可知，對于效率的提升，葉型安裝角扭轉和最大厚度位置移動的提升貢獻度分別約為34%和66%；對于壓力系數的提升，葉型安裝角扭轉和最大厚度位置移動的提升貢獻度分別約為54%和46%.

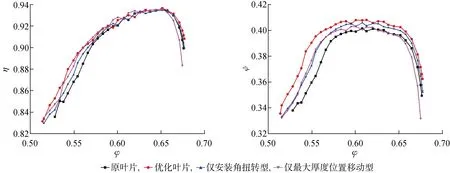
圖18 原葉片，優化葉片，僅安裝角扭轉型優化葉片和僅最大厚度位置移動型優化葉片的特性曲線對比Fig.18 Comparison of characteristic curves of original, optimized, only setting angle rotating, and only maximum thickness position moving blades

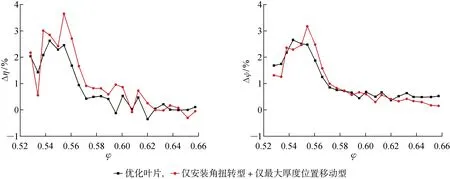
圖19 葉型安裝角扭轉與最大厚度位置移動對原葉片性能提升幅度之和與優化葉片提升幅度對比圖Fig.19 Comparison of performance increments of simply add-up only setting angle rotating and only maximum thickness position moving optimized blades and optimized blades relative to original blades

4 結論

基于高精度且相對高效的Kriging代理模型構建了集成參數建模、網格劃分和CFD仿真的氣動優化系統，對大涵道比渦扇發動機的風扇葉片進行了拓寬穩定運行范圍的優化設計.所采用的大涵道比風扇葉片原始設計比較好，在此基礎上能提升葉片性能，說明優化方法具有可行性，主要結論如下：

(1) 葉片參數化方法是基于葉型安裝角扭轉和最大厚度位置移動兩個因素進行葉型重構.選取特性曲線中的失速點流量為優化的目標函數進行迭代優化，并對優化前后葉片進行了特性對比、幾何形狀對比、流場分析和敏感度分析.

(2) 與原葉片相比，經過優化所得葉片的穩定運行范圍拓寬10.1%，且穩定運行范圍得到提升，效率和壓力系數的最大增幅分別為2.63%和9.27%，表明優化過程有效地拓寬了風扇葉片的穩定工作范圍，并大幅提高了性能.

(3) 從流場方面進行分析，同工況下優化葉片的尾跡損失、吸力面分離、渦流區域面積均有大程度的減小，總體流線分布明顯改善，速度分布合理的區域增大；中上部葉高處的葉片前緣激波強度增加，葉片總體做功能力顯著提升.

(4) 進一步分析優化葉片和因素分離所得葉片相對于原葉片性能提升的幅度可知，優化葉片的穩定運行范圍拓寬和性能提升基本源于葉型安裝角扭轉和最大厚度位置移動按照一定貢獻度的疊加效果.