考慮粗糙地表的近地層風場仿真模擬研究及誤差分析

劉震卿,張 沖,吳曉波,李秋明

(1.華中科技大學 土木工程與力學學院,武漢 430074;2.中建國際投資(河南)有限公司,鄭州 450000)

0 引 言

微地形上空紊流流場預測應用于許多重要工程,例如結構安全、農業風害、航空安全等,在繪制復雜地形風能分布中也發揮重要作用,其決定風力機排布位置。風資源在一些多山地區豐富,但風速分布復雜,因此精確預測復雜地形的風速和紊流強度非常重要。地表粗糙度是反映近地層動力特征的一個重要指標,是研究風場豎向剖面分布的重要參數,因而地表粗糙度對復雜地形風場研究具有重要意義。實際地表大多覆蓋植被或者村落城鎮,若需準確預測這些區域的風能分布情況,首先需要模擬地表粗糙對流場的影響[1-4]。

地表粗糙度長度是邊界層氣象學中常用的一個重要參數,是指在邊界層大氣中,近地層風速向下遞減到零時的高度。根據Pattanapol等[5]對復雜地表粗糙度模擬方法的總結:對于復雜地表粗糙度的模擬方法包括兩種,一種方法是基于湍流模型中的壁面函數法;另一種方法是在湍流模型輸送方程中添加源項加以考慮。

對于壁面函數法,嚴格說來當且僅當計算區域入口處的來流邊界條件與湍流模型及地表粗糙特性相協調時,才能得到水平均勻性的平衡大氣邊界層,但由于湍流的復雜性,在數值模擬中精確實現平衡大氣邊界層常存在困難。Richards和Hoxey[6]基于k-ε湍流模型提出了滿足平衡大氣邊界層的幾個原則,給出了一組來流邊界條件,并對湍流模型參數的取值進行了探討,但在其研究中所給出的湍動能邊界條件為一常數,這與實測以及試驗結果不符。Yang等[7]從標準k-ε 湍流模型方程出發,假設湍流在整個邊界層內處于平衡態,推導出一組隨高度變化的來流邊界條件,并考慮壁面粗糙度,實現了邊界層流場的平衡,但僅滿足湍流能量在邊界層內層范圍才處于平衡。此外使用壁面函數法模擬地表粗糙度的還有Daniel[8]等、唐煜等[9]、鄧院昌等[10]。對于在湍流模型輸送方程中添加源項的粗糙度模擬方法,胡朋等[11]提出通過在湍動能輸送方程與耗散率輸送方程中添加源項的方法,使來流邊界條件與湍流模型相協調,但SST k-ω 湍流模型中各系數很難確定。

另外Fluent提供了多種湍流模型,包括k-ε模型、k-ω 模型和LES等等。但是不同的湍流模型對于求解的適用性也不同,湍流模型的選擇同樣對風場數值模擬結果的精度和資源耗費有著十分重要的影響。

本文基于Fluent流體計算平臺,使用自編UDF程序模擬精細化地表粗糙度,該程序實現了根據由Wind Pro中下載得到的目標區域地表粗糙度長度文件自動添加覆蓋植被阻力源項來模擬精細化地表粗糙度,考慮了計算域內湍流結構信息以及覆蓋植被類型、葉面積密度等相關參數的影響。以Askervein山為例建立數值模型選擇了不同的湍流模型進行風場模擬,與實測數據對比,研究了湍流模型對復雜地形風場CFD 模擬的影響,分析了湍流模型的適用性,并進一步探討了單一地表粗糙度長度的影響。

1 Askervein山實測試驗

Askervein項目[12]是在國際能源署主持下開展的一項關于低山丘陵大氣邊界層的合作研究。Askervein位于蘇格蘭外赫布里底群島南端的南尤伊斯特的西海岸,該山經緯度坐標為(57°11′N,7°22′W),相對高度為116 m,海拔高度126 m。Askervein山體示意圖如圖1 所示,A 線與B 線相交于Askervein山的最高點(HT-Hilltop),AA 線與B 線相交于中心點(CP-Centre Point)。此外還在距離此處3 km 的達利堡附近設置了一個參考點(RSReference Site),用于對與Askervein相遇之前未受干擾的流體運動進行詳細測量。

圖1 Askervein山體示意圖Fig.1 Contour map of Askervein Mountain

在試驗過程中,沿著A、B 和AA 三條線布置了50座以上的測風塔,大多數測風塔高10 m,還有多座更高的測風塔。其中記錄代號為TU03-B 的測風數據發生在1983年10月3日的14:00～17:00風流穩定,風向約210°,由于該山實測數據豐富、便于將數值模擬結果與實測值對比,故本文以Askervein山為研究對象建立地形模型。

PA Taylor等[12]表示,除了附近的一些建筑物以及位于海岸線附近的沙丘之外,Askervein山和周圍地區的地表粗糙度長度基本一致。地表粗糙度長度的初始估測值在0.01～0.05 m,根據參考點RS處的風剖面測量數據表明,地表粗糙度長度的范圍大多在0.01～0.03m 的范圍內。若作為單一的代表值,建議z0取值0.03 m。

2 數值模型與方法

2.1 湍流模型

數值模擬方法主要分為三種[13],包括直接數值模擬DNS、雷諾平均法RANS和大渦模擬LES。作為最準確的湍流模擬方式,DNS 可以直接求解三維N-S方程組,而不需要求平均或近似值來估計和控制誤差,但其對網格精度要求很高,計算量很大,比較耗時;雷諾平均法不需要計算各尺度的湍流脈動,降低了計算量,但無法解析具有較強脈動特征的小尺度渦;大渦模擬直接模擬大尺度紊流運動,利用次網格尺度模型模擬小尺度紊流運動對大尺度紊流運動的影響,但較雷諾平均法更耗時。所以本文選取了后兩種數值模擬方法——雷諾平均和大渦模擬,因而選取了基于雷諾平均法而建立的k-ε 模型、RNG k-ε 模型以及基于大渦模擬的LES模型。

(1)標準k-ε 模型

二維不可壓縮流場質量方程和動量方程為:

式中,ui為平均速度,為雷諾應力,μ 為黏性系數,ρ 為空氣密度,p 為壓強,代表粗糙度阻力源項。湍動能k 和湍動耗散率ε 的運輸方程分別如下式,其中湍流脈動能k 方程為(3)式,湍流耗散率ε 方程為(4)式:

平均速度梯度引起湍動能k 產生了Gk項;標準k-ε湍流模型中的經驗常數C1ε、C2ε、σk、σε一 般取 值如下:C1ε＝1.44、C2ε＝1.92、σk＝1.0,σε＝1.3,μt為 湍 流黏度,表示為μt ＝ρCμk2/ε。Cμ為經驗常數Cμ＝0.09。式中fk和fε為阻力源項,以模擬地表粗糙度對風場的影響。

(2)RNG k-ε 模型

RNG 模型考慮了湍流漩渦的影響,提供了一個考慮低雷諾數流動黏性的解析公式,這些均使得RNG k-ε 模型有更高的計算精度和穩定性,其質量方程和動量方程如(1)、(2)式,湍動能方程和耗散率方程如下所示:

式中,C1ε、C2ε、C3ε為經驗常數,一般取值C1ε＝1.42、C2ε＝1.68、C3ε＝1.72,αk＝αε＝1.393,μeff＝μ+μt,Gb為由浮動引起的湍動能。Rε代表平均應變率對ε影響的附加項。式中fk和fε為阻力源項,以模擬地表粗糙度對風場的影響。

(3)LES模型

湍流運動可以看做是由很多尺度大小不同的渦組成的,大尺度渦比小尺度渦運動更劇烈,具有各向異性的特點,對于湍流的平均運動影響更明顯,可以實現動量、質量和能量等的交換;小尺度渦相對通常較弱,主要通過非線性的作用對大尺度渦的運動產生影響,作用主要表現為耗散[13],因為共性更多,近似于各向同性。不可壓常黏性系數的連續性方程和N-S方程為:

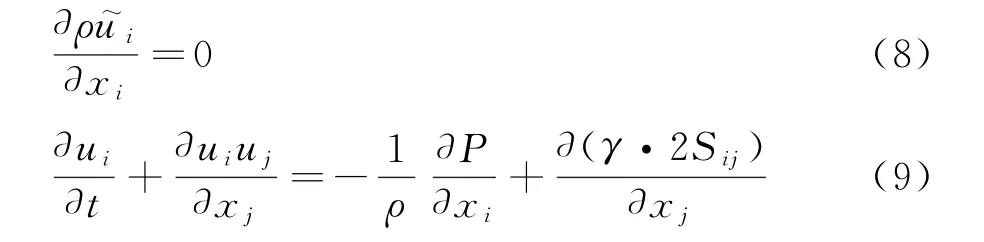
式中,Sij為拉伸率張量,Sij＝(?ui/?xj+?ui/?xj)/2;ρ為為流體密度;γ 為分子黏性系數。濾波后的動量方程如(10式),其中f~u,i為考慮地表粗糙度阻力源項。

亞格子模型采用Smagorinsky-Lilly,亞格子應力(SGS)的表達式如下:

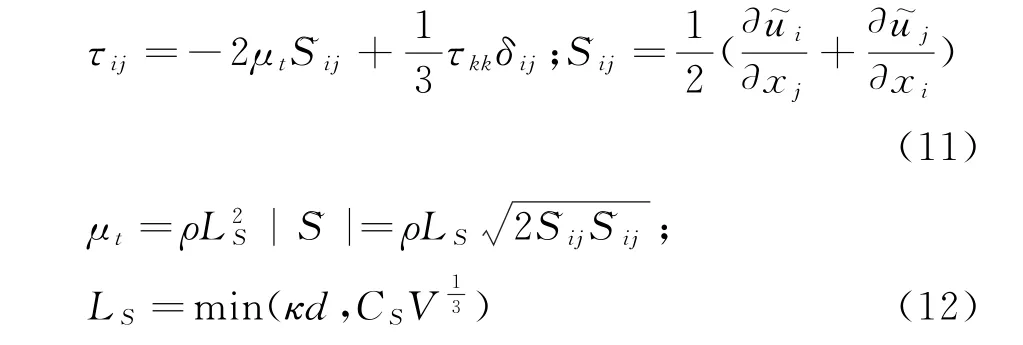
式中,Ls—亞格子的混合長度;κ—卡門常數,κ＝0.42;d—壁面網格到壁面的距離;V—控制體體積。

三種湍流模型使用Fluent求解三維非穩態Navier-Stokes方程,空間離散方式采用有限體積法,二階中心差分格式用于對流項與黏性項,二階隱式格式用于非穩態項的時間推進;壓力的插值格式將選取標準格式;SIMPLE算法用于壓強速度解耦。

2.2 粗糙度模擬

本文采用在計算域內添加阻力源項的方法來模擬地表粗糙度。為了考慮地表粗糙區域對流場的阻礙作用,通過在Navier-Stokes動量方程中加入阻力源項加以考慮,在阻力源項的計算中,需要首先確定粗糙元的阻力系數,針對此參數已開展過相關試驗研究,并給出了經驗取值。由于Askervein山地表粗糙元為覆蓋植被,根據Enoki和Ishihara[10]的研究,當粗糙區域粗糙元為覆蓋植被時,采用表達式:

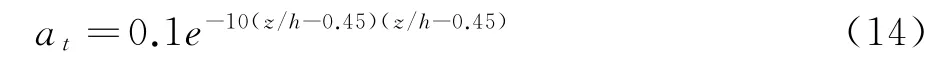
上式中,z 為距離地表高度,h 為植被高度。對于不同地表覆蓋情況,粗糙度長度z0與覆蓋植被高度h滿足h＝a×z0,a 為兩種粗糙度表征參數的轉換系數。本文根據既有研究,選取轉換系數a＝20.0[12],抗力系數CD,t＝0.4[10]。

對于k-ε 模型湍動能和湍動耗散率的運輸方程中的阻力源項fk和fε由Enoki與Ishihara[10]提出的阻力源項計算方法求得:

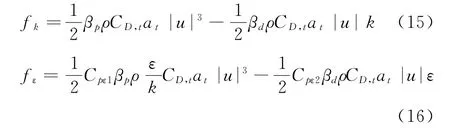
式中,u 為速度大小,βp＝1.0,βd＝4.0,Cpε1＝1.5,Cpε2＝0.6。

2.3 網格模型

考慮到后續邊界條件的設置以及最高點HT 的高度,計算域長寬高設置為6 km×6 km×1.5 km,底面中心點為Askervein山的最高點HT 如圖2(b)所示,為使地形平穩過渡到光滑地區,設置寬0.4 km 的過渡區圓環如圖2(a)。建立網格模型時,參考Askervein山的尺寸,以最高點HT 所在垂線為中心,半徑1 km 的圓柱體區域內進行網格細化加密,網格分辨率為15 m 如圖2(c),以精確顯示此地的地形地勢。山體周圍逐漸過渡到平坦地形,設置網格尺寸平穩的從加密區過渡到邊界處,最大網格分辨率為80 m。垂直方向上在近地面進行網格加密最小網格尺寸0.05 m,以準確捕捉近地面流場,采用相鄰網格尺寸比值為一定值的σ 網格;為減少由于網格尺寸急劇變化而帶來的數值誤差,計算域內網格最大生長率為1.2;網格總量約為200萬。采用非結構化三棱柱網格,以充分擬合幾何邊界,同時也可以保證每層單元拓撲結構的一致性。圖2為CFD 三維實際地形模型示意圖。

圖2 CFD三維實際地形模型及網格分布示意圖Fig.2 CFD three-dimensional actual terrain model and grid distribution diagram

2.4 邊界條件

計算域左側采用速度入口,右側采用壓力出口,四周壁面采用對稱邊界條件(?u/?n＝0,?w/?n＝0,v＝0),底面采用無滑移邊界條件(u＝0,v＝0,w＝0,?p/?n＝0)。根據Richards等[6]的大氣邊界層理論,入口處速度選擇參考點RS處210°風向角時測風塔的風速,采用以下模型:

式中,u*為摩擦速度,κ＝0.4[6]為卡門常數,z0為地表粗糙度長度。根據參考點RS 測風數據得到:u*＝0.618 m/s,z0＝0.03[16]。使 用 標 準k-ε 模 型 和RNG k-ε 模型時,入口邊界的湍動能、耗散率依次設置為:

式中,hg＝891.82 m,當高度超過界限值后,湍動能趨于零,取值0.0001。

董喜陽，1986年生于吉林九臺。文學碩士。詩人、作家，兼事文學、美術評論。魯迅文學院第三十四屆中青年作家高級研討班（青年作家班）學員。中國作協會員。作品散見于《詩刊》《人民日報》《大家》《詩選刊》等刊物。現居長春。

3 湍流模型分析

3.1 風速比

Askervein試驗包括不同的來流風速,為了便于分析數值模擬的計算結果,在此便不能使用實際風速進行比較,通常使用一個無量綱參數風速比S 來描述風加速效應。

上式中,U(z)表示距離地面高度z 處的風速,U0(z)為入口處距離地面z 高度處的風速,取z＝10 m。定義風速比標準偏差衡量計算結果與實測結果的偏差,風速比標準偏差由下式計算:

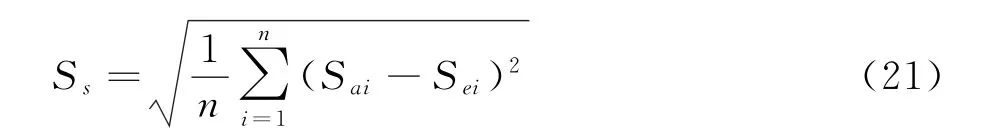
式中,n 為測風點個數,Sei表示第i 個測風點距離地面10 m 高度的風速實測值與入口基準點RS相同高度的風速實測值的風速比,Sai表示第i 個測風點離地面10 m 高度的CFD 數值模擬風速值與入口基準點RS相同高度的風速實測值的風速比。

3.2 精細化粗糙地表模擬

從WindPro中下載包含Askervein山的計算域范圍內的地表粗糙度長度文件,通過自編程序插值得到計算域內網格節點處粗糙度長度。圖3顯示了計算域內地表粗糙度長度分布情況,可以看出地表粗糙度長度分布在0.01～0.05 m 范圍內。

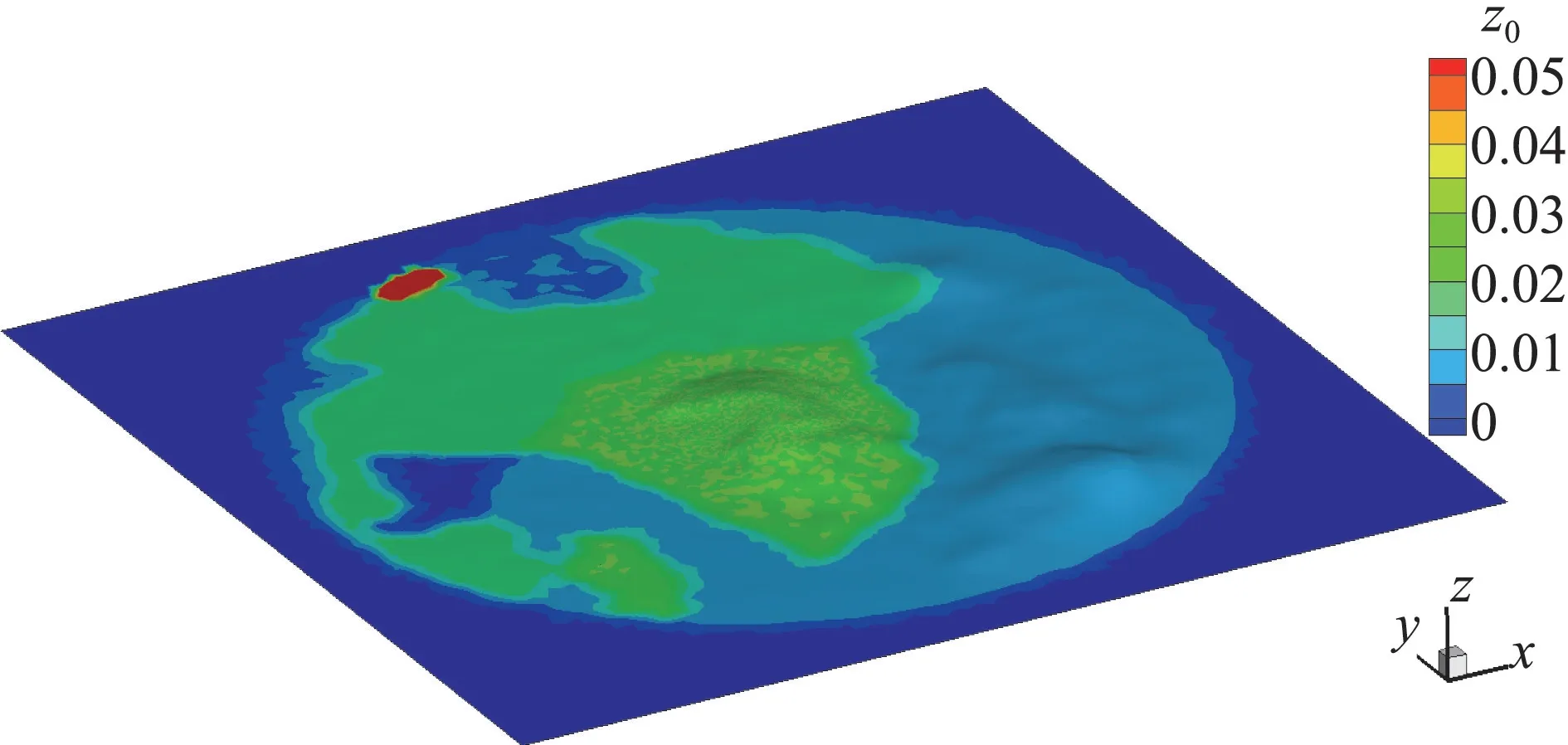
圖3 計算域內地表粗糙度長度分布圖(單位:m)Fig.3 Roughness length distribution in computational domain(unit:m)

3.3 10 m 高度處風速比

基于精細化地表粗糙度模擬,選用三種不同湍流模型進行風場模擬。沿AA 線和B 線布置的10 m高測風塔,均可以獲得比較全面的數據,由于A 線和AA 線之間具有幾何地形的相似性,因此僅對貫穿山體中心的AA 線和B 線進行10 m 高度處風速比分析。圖4、5分別顯示了沿AA 線和B 線10 m 高度處的風速比與實測數據[17]的對比,圖中柱狀圖分別代表各湍流模型相比實測值的風速比標準偏差。

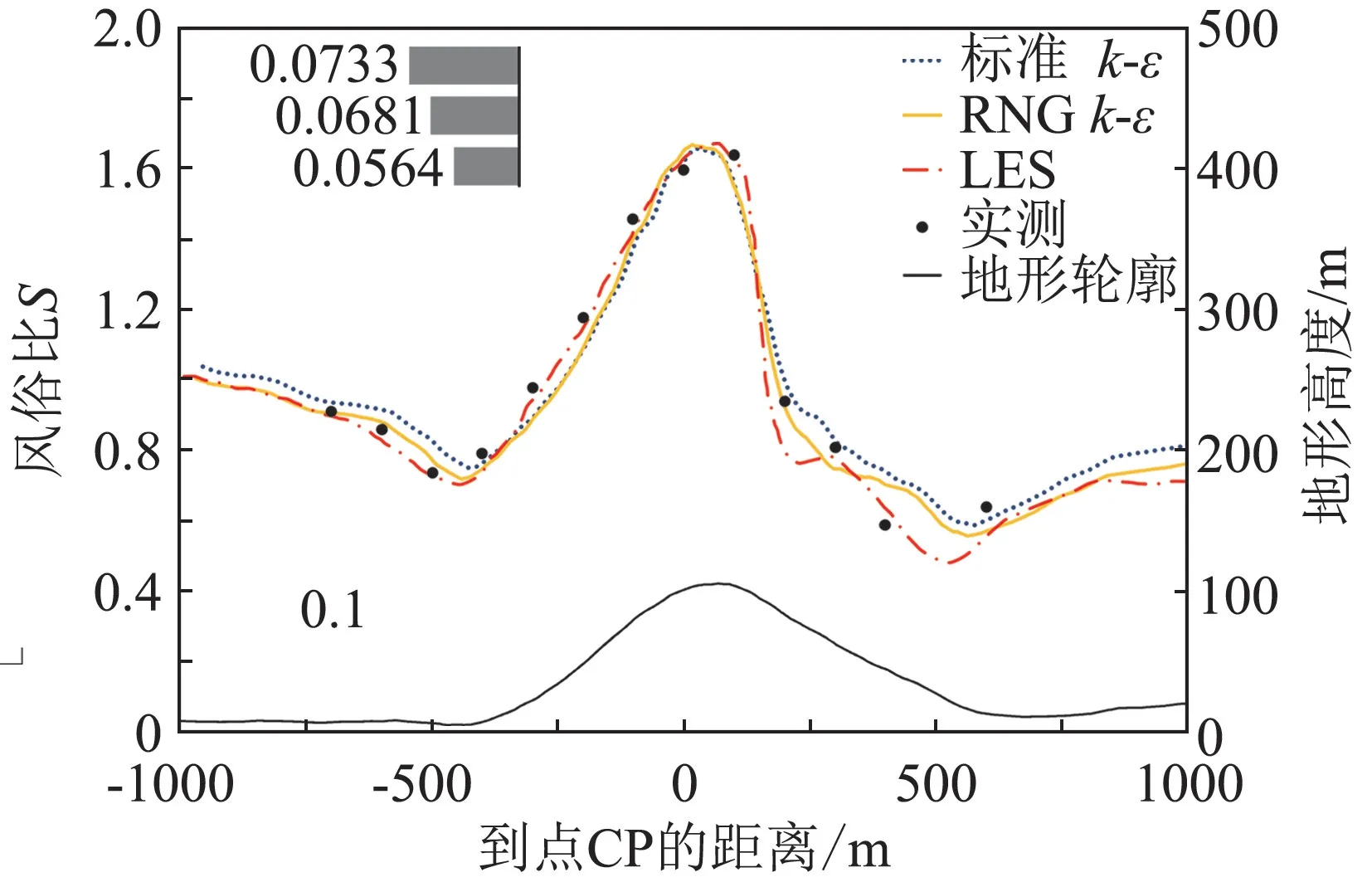
圖4 沿A線10 m 高度的風速比Fig.4 Wind speed ratio at 10 m along line A

從圖4中可以看出,沿AA 線10 m 高度處風速在遇到山體阻礙后風速降低,到達山頂產生較大的風加速,隨后在背風面處風速迅速降低。三種湍流模型風速比計算結果在迎風面趨勢一致,均與實測值吻合較好,其中LES模型吻合更好;在背風面則顯示出一定誤差,主要由于在背風面發生流動分離,導致誤差產生,但LES模型可以捕捉背風面風速迅速下降的現象。整體上LES計算結果標準偏差為0.0564,相比于標準k-ε 模 型 結 果0.0733 和RNG k-ε 模 型0.0681誤差均要小,精度更高。

圖5對比了三種湍流模型計算結果沿B線10 m高度處風速比和實測數據。B線為山脊線,可以發現隨著山脊升高,風速比也隨之增大,這是由來流方向垂直于B線,山脊越高風加速效應越明顯,導致風速比越大。整體上LES計算結果相比于實測值偏差最小為0.0758。而標準k-ε 模型和RNG k-ε 模型結果偏差分別為0.1412、0.1217,兩者計算結果差別不大,但誤差均大于LES模型。

圖5 沿B線10 m 高度的風速比Fig.5 Wind speed ratio at 10 m along line B

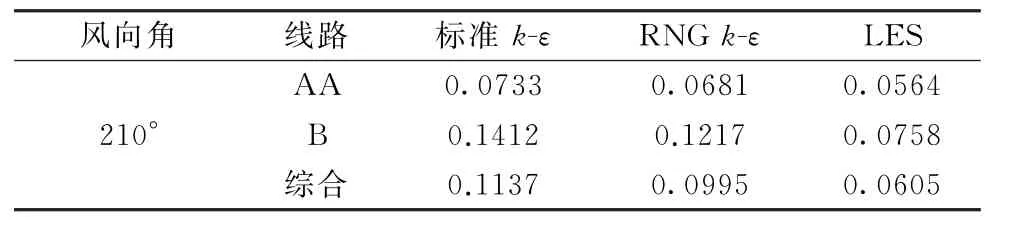
表1 三種湍流模型風速比標準偏差分析Table 1 Analysis of wind speed ratio standard deviation under

3.4 風剖面

三種湍流模型在點HT 處風剖面風速比計算結果對比如圖6所示。從圖中可以看出三種湍流模型在HT 處的風剖面風速比曲線與實測值基本一致,但是在近地面,LES的峰值大于其余兩種湍流模型,更接近實測值,誤差更小;標準k-ε 模型和RNG k-ε模型在5～20 m 高度時接近風速比實測值,但在高處風速計算結果明顯偏大。LES模型計算結果與實測值偏差11.7%,相比于標準k-ε 模型和RNG k-ε 模型偏差分別下降了7.7%和2.7%,模擬誤差更小。

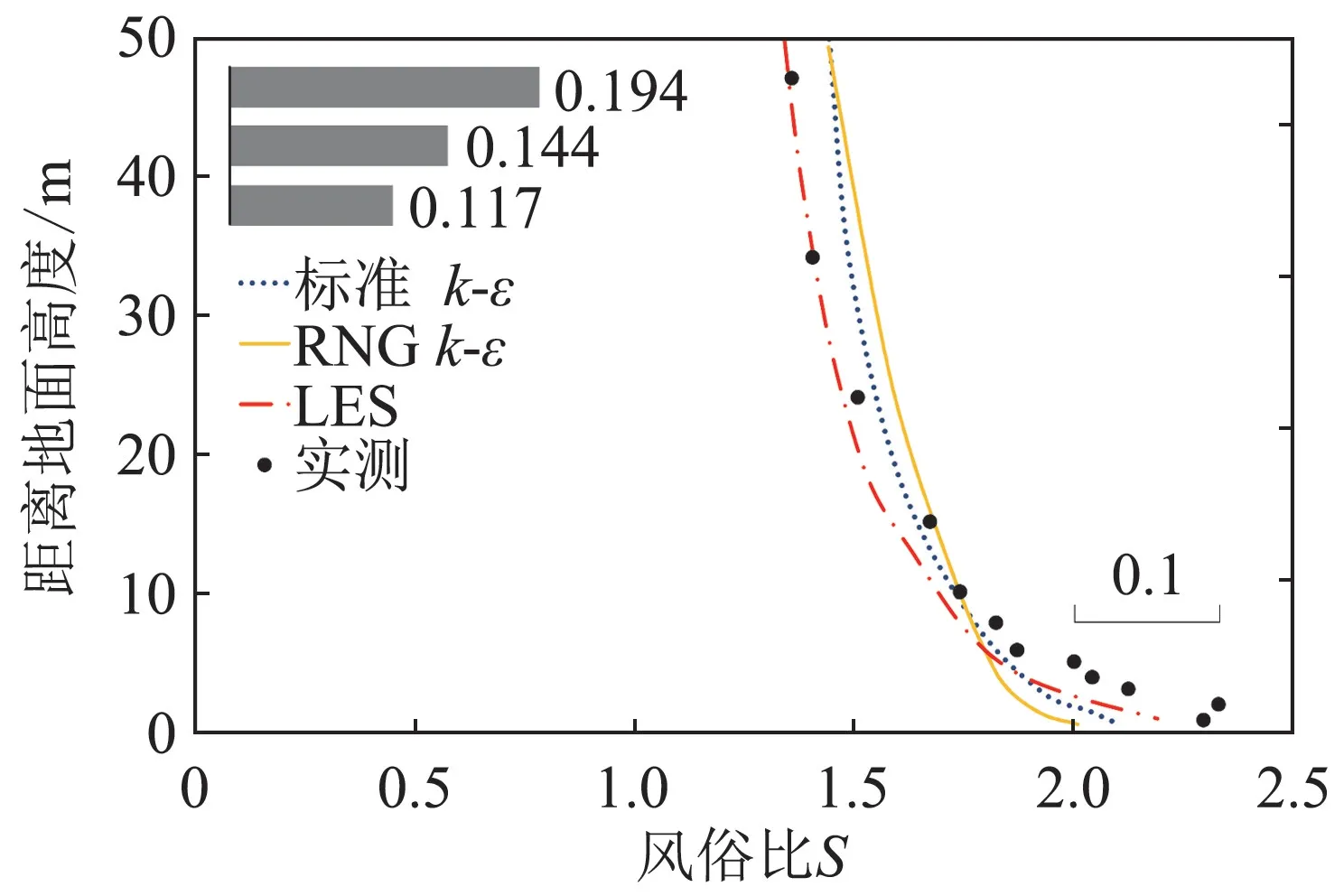
圖6 HT處的垂直風剖面風速比Fig.6 Vertical wind profile wind speed ratio at HT

3.5 湍動能

Askervein山布置的測風塔中沿A 線分布的測風塔主要用于采集湍流數據,故將三種湍流模型模擬得到沿A 線10 m 高度處的湍動能分布于實測結果對比,如圖7 所示,其中湍動能標準偏差定義同式(17)。由圖可以看出湍動能在山頂減小,隨后在距離山頂大約200 m 的背風面附近達到極大值。三種湍流模型計算結果中LES與實測結果吻合最好,標準偏差為0.4191,相比于標準k-ε 模型和RNG k-ε 模型0.9376、0.8860均要小。

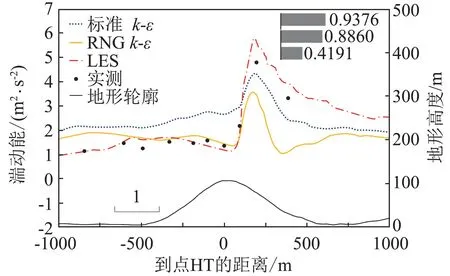
圖7 A線10 m 高度處湍動能分布Fig.7 Turbulent energy of line A at 10 m hight

圖8 HT處垂直方向的湍動能Fig.8 Vertical turbulent energy at HT

三種湍流模型在點HT 處垂直方向上湍動能分布如圖8所示。圖8顯示,雖然三者的趨勢基本一致,但是標準k-ε 和RNG k-ε 模型計算結果明顯比實測值大,由于標準k-ε 和RNG k-ε 無法解析具有較強脈動特征的小尺度渦,尤其在近地面處,表明在此處并不適用,而LES模型能較好捕捉近地面的小尺度渦進而模擬值與實測值基本吻合,誤差更小。LES、RNG k-ε 和標準k-ε 對點HT 垂直方向的湍動能模擬結果的標準差分別為0.3951、1.3467和0.8702,相比之下LES更為精確。

4 單一地表粗糙度

上一小節討論了基于精細化地表粗糙度模擬下不同湍流模型的性能,結果表明,相比于其他幾種湍流模型,LES模型計算結果精度更高。但通常難以獲得較精確的精細化地表粗糙度分布,本節為了探明模擬復雜地形風場時,單一地表粗糙度能否獲得理想結果,選擇LES湍流模型,設置地表粗糙度長度z0分別為0.00,0.01,0.02,0.03,0.04,0.05,0.06,工況設置如表2所示。

模擬不同工況下的風場,將距離地面10 m 高度的風速轉換為風速比,與實測值[17]進行比較。圖9、圖10和圖11分別顯示了沿A 線、AA 線和B線距地10 m 高度處模擬風速比與實測數據的對比,圖中柱狀圖分別代表各湍流模型相比于實測值的風速比標準偏差。

從圖9～圖11可以看出,地表粗糙度長度對實際地形的CFD 數值模擬結果影響比較大。當地表粗糙度長度設置為0.00時,即采用光滑地表不考慮粗糙度長度對風場的阻礙作用,在A 線、AA 線的所有測風點以及B線大部分測風點處的數值模擬結果明顯遠大于實測風速值,同時也大于各個粗糙度工況的模擬結果。對于粗糙度長度的設置,從圖9～圖11均可看出隨著地表粗糙度長度的增大,各測點的數值模擬風速值逐漸降低。當地表粗糙度長度設置為0.06 m 和0.05 m 時,整體的風速模擬值遠小于實測值,標準偏差較大。而當地表粗糙度長度設置為0.02～0.04 m 時,整體的風速比曲線與實測值的吻合度較高,表明該地形的地表粗糙度長度的平均值接近0.03 m,與實際地表植被平均分布情況一致[17]。

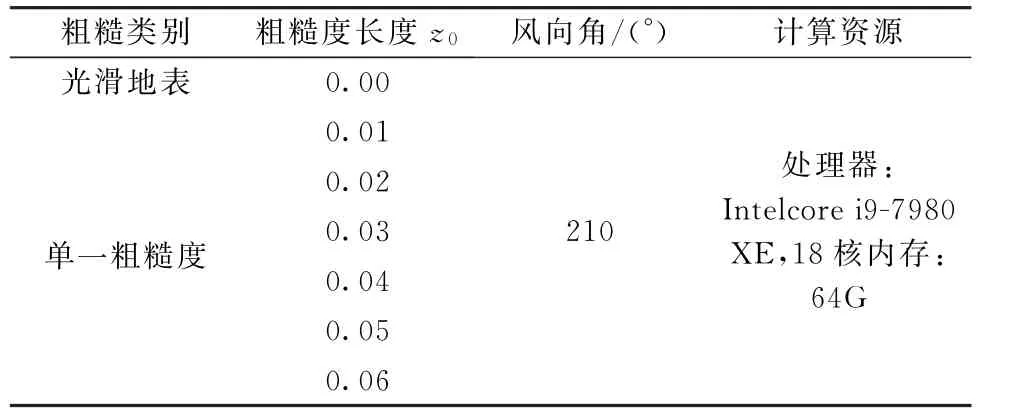
表2 工況匯總表Table 2 Summary of cases

圖9 沿A線10 m 高度的風速比Fig.9 Wind speed ratio at 10 m along line A

圖10 沿AA線10 m 高度的風速比Fig.10 Wind speed ratio at 10 m along line AA

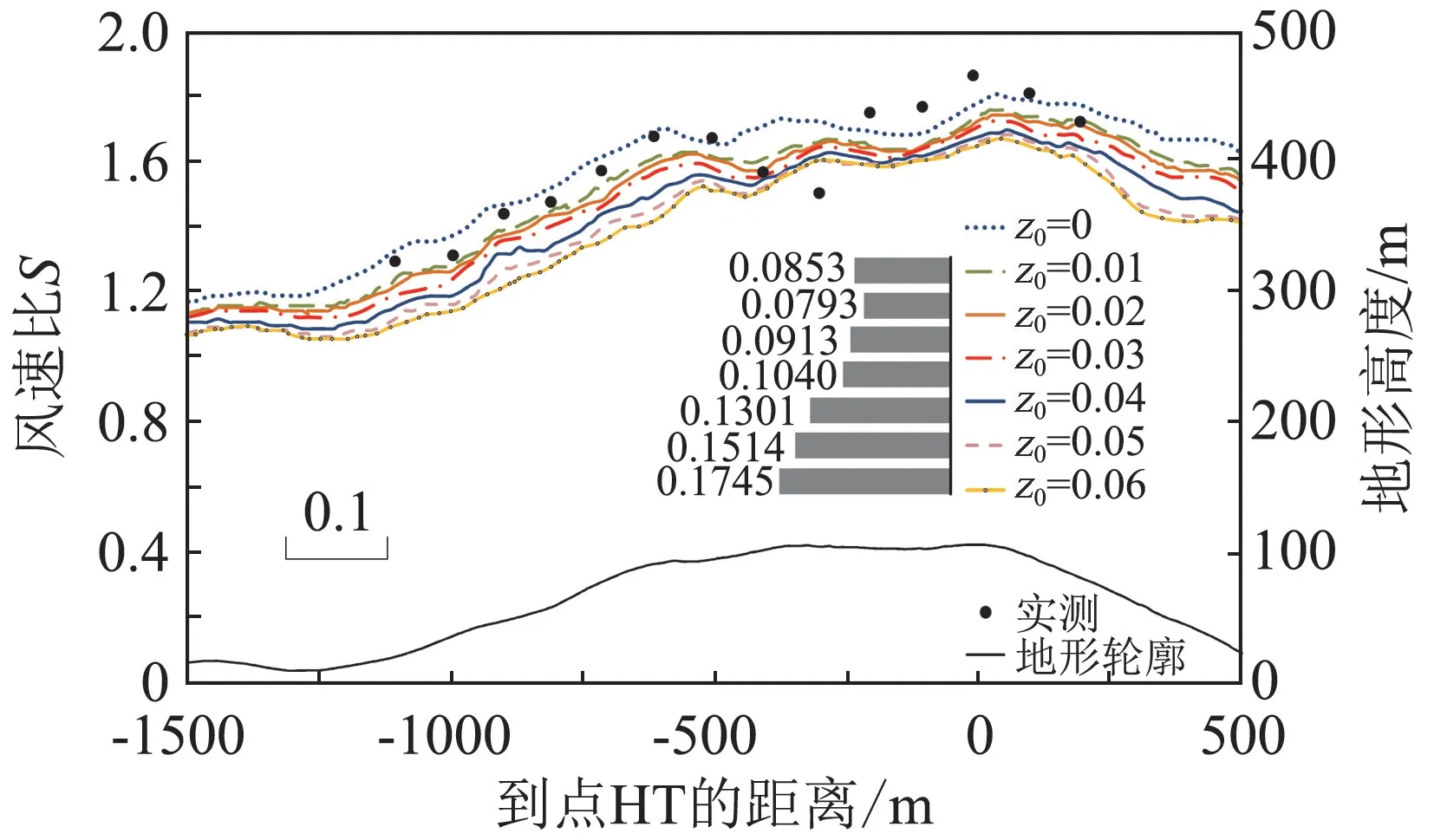
圖11 沿B線10 m 高度的風速比Fig.11 Wind speed ratio at 10 m along line B

另外從圖9和圖10中,可以看到在迎風面山坡,地表粗糙度長度為0.02 m 時風速比與實測值吻合較好;在背風面山坡,地表粗糙度長度為0.04 m 時吻合較好,表明該地區地表粗糙度長度分布的差異性。

同時與采用單一地表粗糙度長度工況結果對比,統計各工況所有測點風速比相比于實測值的標準偏差如表3所示。由表3可以看出,當地表粗糙度長度設置為0.02～0.03時,模擬風速比誤差為0.0663～0.0784相比于精細化地表粗糙下模擬誤差0.0620十分接近,而當單一地表粗糙度長度小于0.02或大于0.03時,模擬風速比誤差則過大,證明了模擬復雜地形風場時合理設置單一地表粗糙度能有效減小模擬誤差,滿足精度要求。

表3 各工況風速比標準偏差Table 3 Wind speed ratio standard deviation of different cases

5 結 論

本文基于計算流體力學方法,實現了通過自編UDF程序實現根據地表粗糙度長度添加覆蓋植被阻力源項來模擬地表粗糙度,以Askervein山為例,研究了標準k-ε、RNG k-ε 和LES三種湍流模型對風場模擬的影響,進一步探討了地表粗糙度長度的影響,得出以下結論:

1)三種湍流模型均能捕捉迎風面風速變化,誤差較小,而在背風面由于流動分離產生一定的誤差,但LES模型可以捕捉到背風面風速迅速下降的現象。整體上LES模型偏差為6.05%,相比于標準k-ε模型11.37%和RNG k-ε 模型9.95%,LES模型誤差最小;

2)標準k-ε 模型和RNG k-ε 模型模擬結果風剖面風速比與實測值偏差較大,LES模型模擬結果相比于標準k-ε 模型和RNG k-ε 模型結果誤差分別減小了7.7%和2.7%,與實測值最吻合,誤差最小;

3)湍動能在山頂達到極小,隨后在距離山頂大約200 m 的背風面湍動能出現極大值,相比于其他兩種湍流模型,LES模型能更準確捕捉近地面湍動能信息,與實測值吻合最好,誤差最小;

4)地表粗糙度長度對CFD 數值模擬結果影響比較大。風速會隨著地表粗糙度長度的增大而逐漸降低;地表粗糙度長度對風場的影響在迎風面和背風面處有較大的差異性;合理設置單一地表粗糙度能有效減小模擬誤差,滿足精度要求。