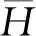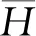炸藥背基對爆炸沖擊載荷的影響分析

劉聰，張世聯

(上海交通大學 船舶海洋與建筑工程學院，上海 200240)

對于自由場爆炸載荷作用下板結構的動力響應問題已有相對較多、較全面的研究。對于內部爆炸，由于密閉空間的限制作用，沖擊波會在結構內部發生多次反射和匯聚，導致目標板出現二次或多次加載的情況，同時密閉空間內會存在較長時間的持續高壓(準靜態壓力)，其沖擊過程較復雜。眾多學者在內爆載荷[1，2]、密閉結構的變形[3-5]和破壞模式[6]，以及準靜態壓力[7]等方面亦取得了一定的研究成果。但是理想的自由場和密閉環境在工程實際中非常少見，更多的沖擊環境介于這兩者之間。比如，當炸點或者目標板附近存在障礙物時，或者當容器的一面或多面敞開的時候。工程實際中的一個典型情況是背基爆炸，即炸藥被放置在地面、水泥或剛性基座上進行引爆。與內部爆炸相似，發生背基爆炸時，炸藥背基會將沖擊波向目標板反射，使目標板受到更大的沖擊載荷。但不同的是準靜態壓力卻不會產生。因此，背基爆炸問題值得探討。已有的研究通過試驗和仿真的方法分析炸藥背基對金屬板所受爆炸沖量和塑性變形的影響，發現在炸藥下方布置剛性背基后，炸藥上方的金屬板受到的脈沖值和塑性變形均顯著增大[8]。但是并未對這種現象進行規律性的研究。為此，考慮以一正方形固支方板為對象，通過改變炸藥質量和相對爆距，分析背基爆炸時爆炸沖量增強幅度隨這些參數的變化規律，提出背基爆炸沖量增強因子的經驗計算公式。

1 計算模型

1.1 幾何模型

建立自由場爆炸和背基爆炸幾何模型見圖1。自由場爆炸模型由一塊固支正方形板和一個半球形炸藥組成。其中，方板的半寬值L=100 mm、厚度t=3 mm，半球形TNT炸藥位于方板中心點正上方H處，見圖1a)。背基爆炸模型在自由場爆炸模型的基礎上，在半球形炸藥背后布置一個固定剛性壁，見圖1b)。

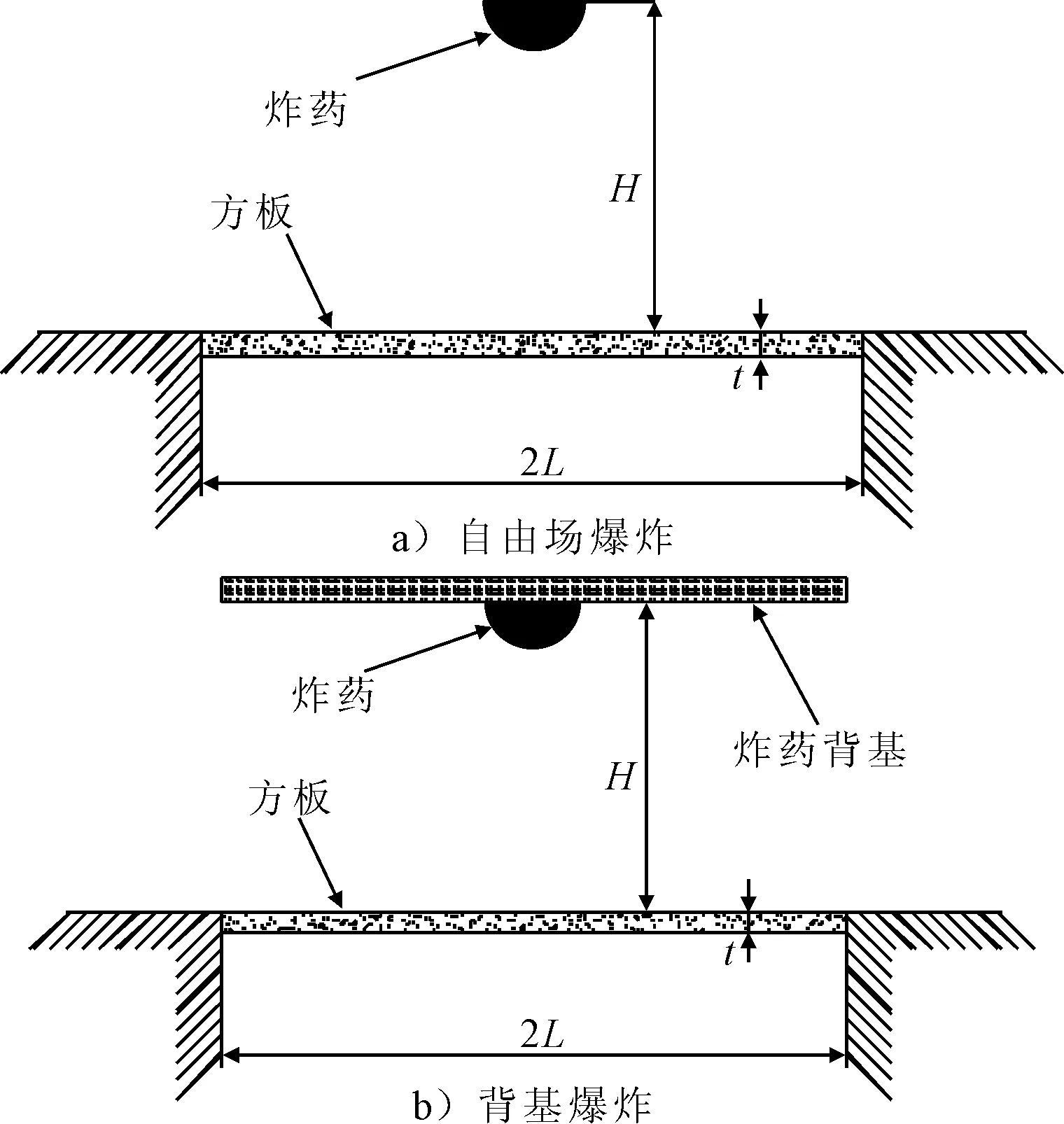
圖1 爆炸模型

定義相對爆距為

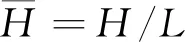
(1)

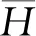
1.2 材料模型及參數

板的應力與應變關系近似為雙線性彈塑性材料，以真實應力對應等效塑性應變的方式處理。密度7.85×103kg/m3，彈性模量2.1×105MPa，泊松比0.3，靜態屈服應力235 MPa，硬化模量250 MPa，失效應變0.28。采用能考慮動態應變率效應的Cowper-Symonds模型，同時考慮材料應變強化效應，其本構方程如下[9]。

(2)

(3)

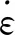
采用gamma律狀態方程EOSFAM描述空氣：

p=(γ-1)·ρ·e

(4)

式中：e為單位質量比內能，取0.21×106J/kg；ρ為空氣密度，取1.25 kg/m3；γ為比熱比，取1.4。

TNT炸藥用高能密度空氣模擬，其密度為1 600 kg/m3，能量密度為4.2×106J/kg。

1.3 耦合模型

采用MSC.Patran進行有限元建模，限制目標方板四邊節點6個自由度全部為零。目標板以拉格朗日單元模擬，炸藥和空氣以歐拉單元模擬，二者以一般耦合法進行耦合。采用瞬態非線性動力學分析程序MSC.DYTRAN對模型進行計算，歐拉單元采用具有二階精度的ROE求解器進行求解，拉格朗日單元采用顯示積分方法對時間域進行求解，計算時間為3 ms。

根據一般耦合法的要求，在建模時需要添設虛元與拉格朗日單元組成封閉六面體耦合面。自由場爆炸和背基爆炸耦合模型見圖2。

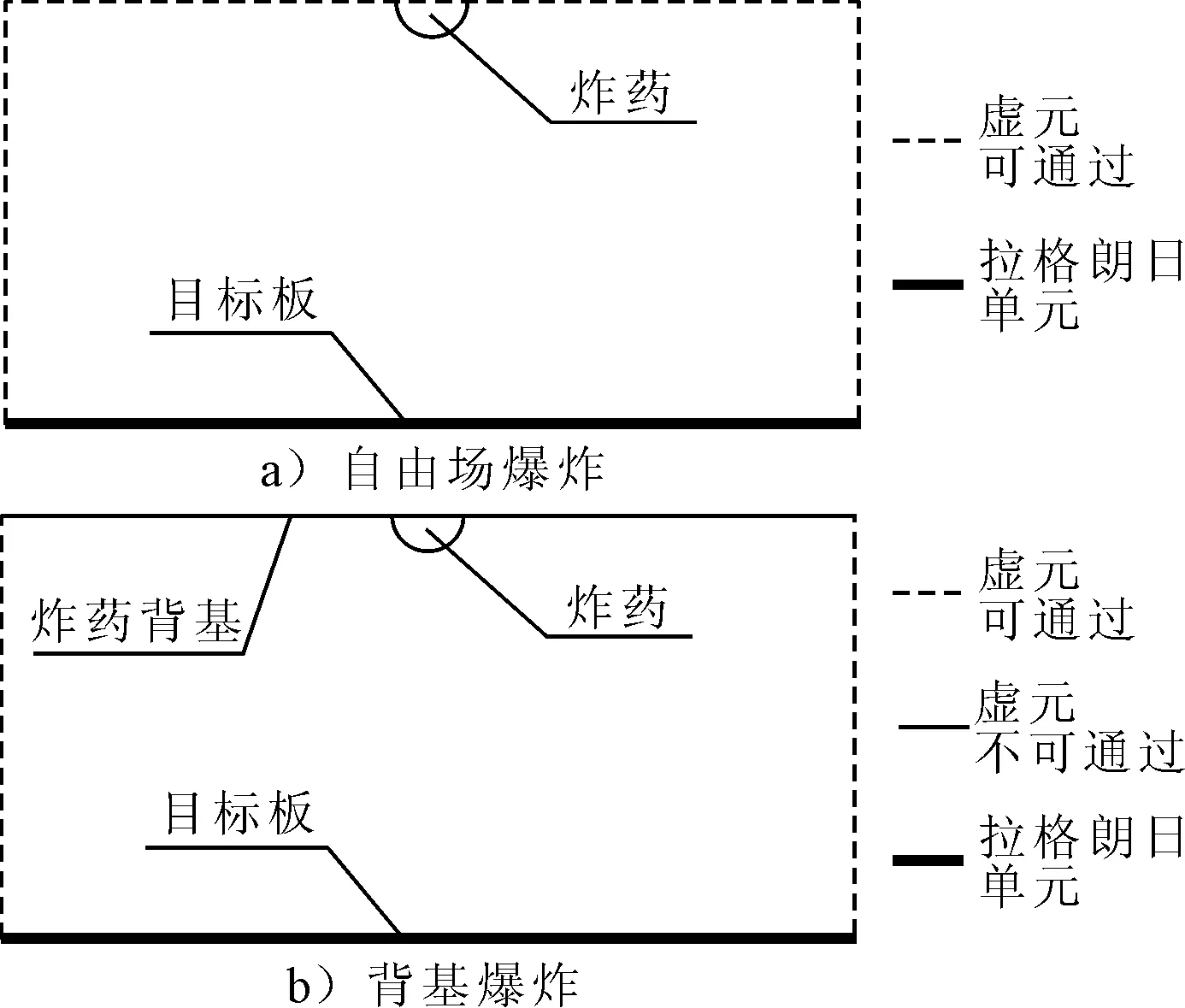
圖2 有限元模型耦合面示意

在自由場爆炸的耦合模型中，目標板為拉格朗日單元，其他五面為虛元，設置爆炸沖擊波可自由通過虛元，見圖2a)。在背基爆炸耦合模型中，目標板為拉格朗日單元，炸藥背基為虛元，并設置沖擊波不可通過該虛元，其他四面仍為可通過的虛元，見圖2b)。

1.4 網格密度

采用大小不同網格對爆距為100 mm、炸藥質量為60 g時自由場空爆載荷下目標方板的動力響應進行試算。所選用的網格大小及計算結果見表1。

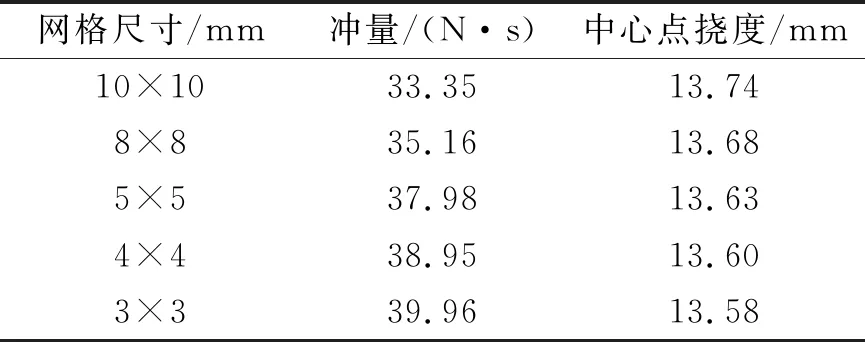
表1 網格參數及計算結果

根據表1計算結果的收斂性并綜合考慮仿真計算的時效性，選擇網格尺寸為4 mm×4 mm。相應目標板有限元模型及坐標系見圖3，其中長、寬和高度方向分別為x、y和z軸方向。

圖3 方板有限元模型

1.5 計算工況

采用控制變量法，對不同炸藥質量和相對爆距時，目標方板所受到的爆炸沖量進行計算。計算工況見表2。

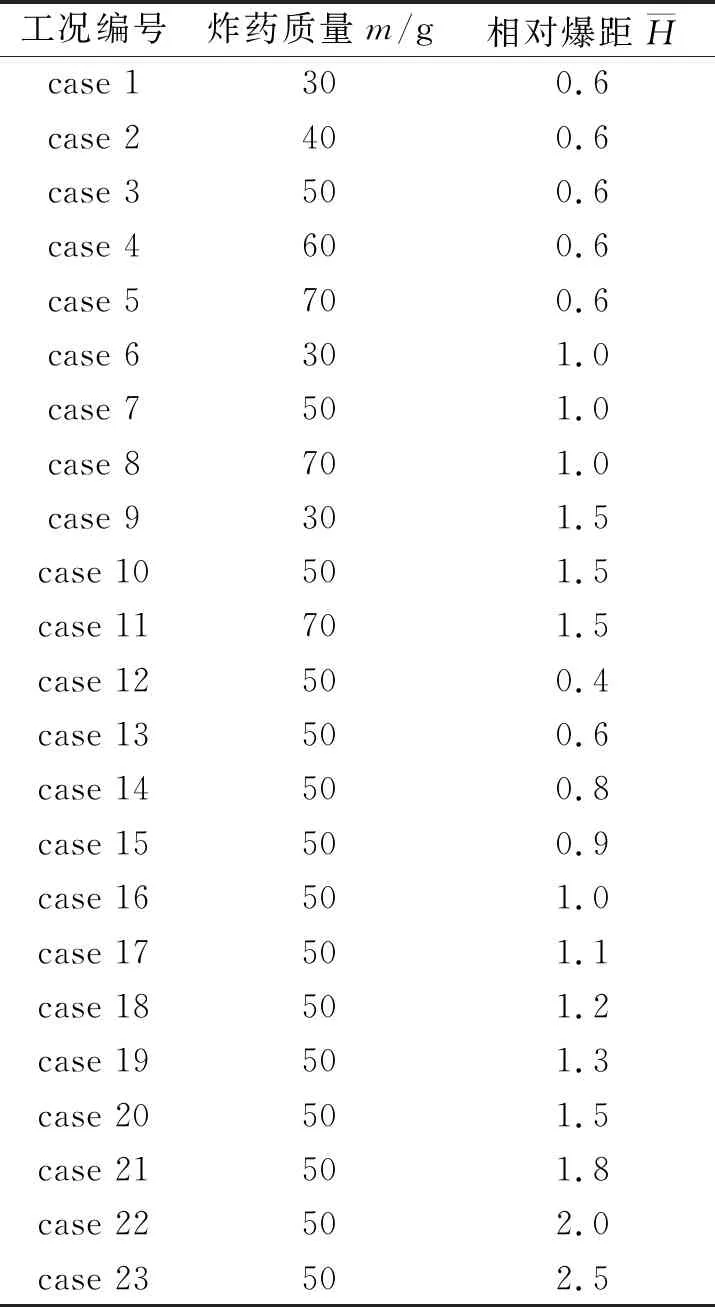
表2 計算工況

2 計算結果與分析

2.1 炸藥質量的影響

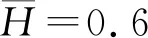
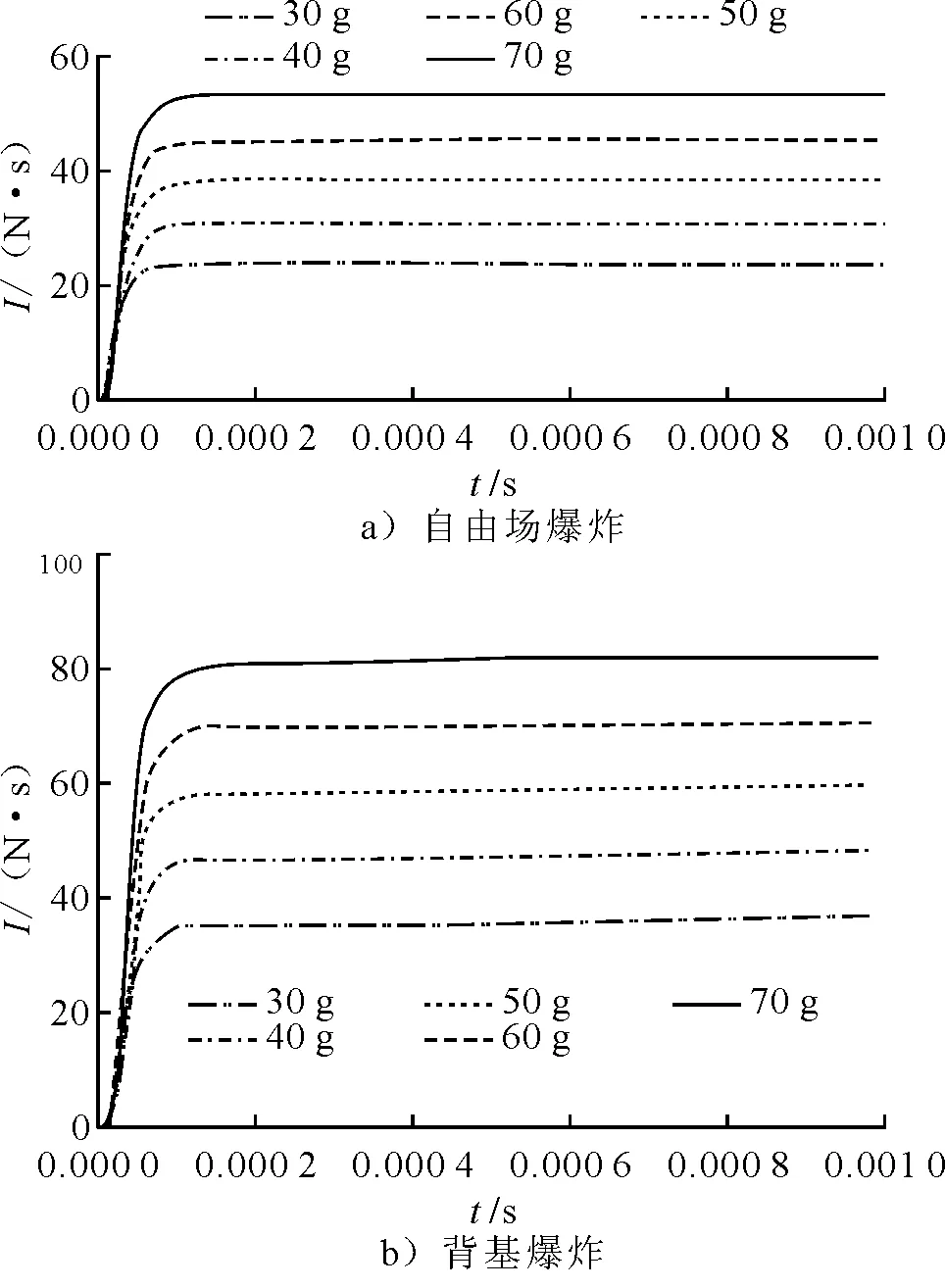
圖4 不同炸藥質量下爆炸沖量時歷曲線

由圖4可知，炸藥質量相同時，背基爆炸的爆炸沖量顯著大于自由場爆炸的爆炸沖量。這是因為炸藥背基阻止了爆炸沖擊波向后方傳播，并將這部分沖擊波向目標板反射，從而增加了作用在目標方板上的沖擊波總量，因此，沖擊載荷增大。

為了量化的研究炸藥背基對爆炸沖擊載荷的增強效果，定義沖量增強因子為

(5)

式中:Ib為背基爆炸時目標方板受到的爆炸沖量；I0為自由場爆炸時目標方板所受到的爆炸沖量。

3種相對爆距在不同炸藥質量下(case 1～case 11)對應的沖量增強因子見圖5。

2.2 相對爆距的影響

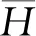
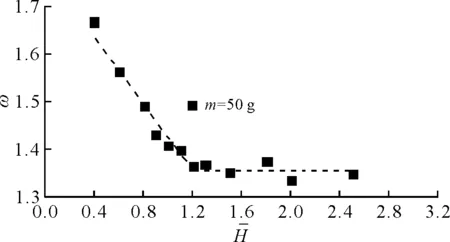
圖6 沖量增強因子隨相對爆距變化趨勢

根據圖6中沖量增強因子隨相對爆距的變化趨勢，總結出如下雙折線形式的經驗公式。

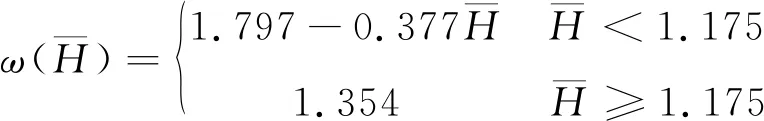
(6)

根據式(6)計算case 12～case 23的沖量增強因子，結果見表3。

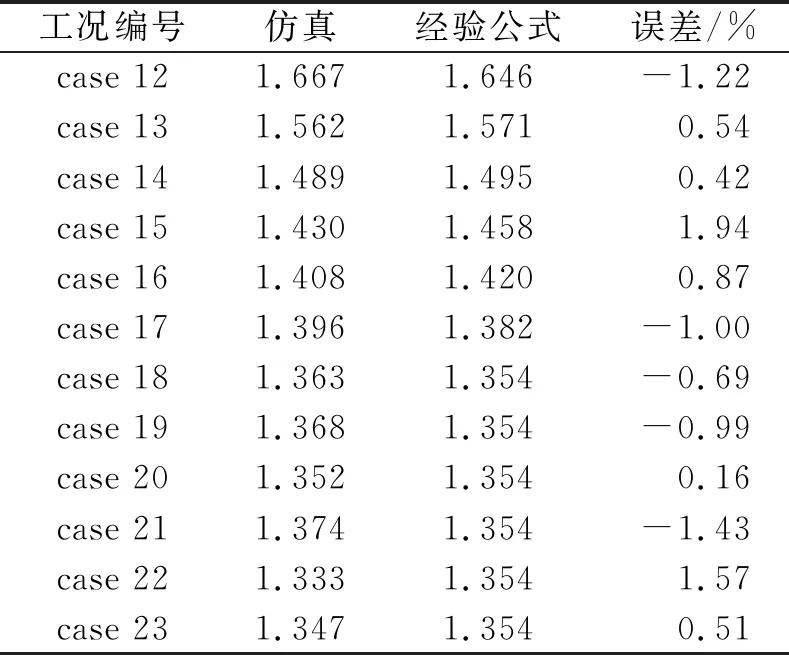
表3 沖量增強因子ω仿真與公式計算結果對比

由表3可知，各工況下經驗公式計算結果與仿真結果間的誤差均在2%以內，說明該公式具有很好的準確性。

3 結論