超彈性材料本構關系的最新研究進展1)

彭向峰 李錄賢

(西安交通大學航天航空學院,機械結構強度與振動國家重點實驗室,陜西省先進飛行器服役環境與控制重點實驗室,西安 710049)

引言

工程實際中常見的聚合物、橡膠、凝膠等高彈體以及諸如動脈、肌肉、皮膚等生物物質[1],具有高彈性、抗震性、耐磨性等許多優良的性能[2].纖維增強超彈性復合材料更是因為具有熱解溫度高、耐老化等特點,被廣泛應用于固體火箭發動機絕熱包覆層中[3-4].這些材料,一般都具有隨機取向的分子鏈網絡結構,由于分子間相互作用力弱、分子鏈間交聯點稀疏等特點[5],能夠經歷很大變形,且在加載循環結束后沒有能量耗散,被稱為是超彈性材料.

不同領域研究者對超彈性材料的關注角度不同.數學家關注應變能函數的存在性、客觀性及對稱性等基本特性; 材料學家關注如何運用模型預測和描述實驗現象; 應用領域的科技工作者關注的則是通過描述特定實驗數據,對超彈性材料器件的復雜響應進行數值模擬[6].可以看出,建立超彈性材料的本構關系是所有領域研究者普遍關注的核心問題[7].

斷裂分析是材料本構關系應用的典型問題,復雜變形模式和大變形構成的近裂尖區完整形貌決定了材料的斷裂行為.線彈性斷裂力學雖簡潔完美,但由于線彈性理論在描述較大變形方面的局限,嚴格意義上不適用于裂尖場分析.超彈性材料本構模型彌補了線彈性模型在這方面的缺陷,是研究裂尖大變形行為的理想選擇.然而,由于非線性問題的復雜性和多樣性,人們對超彈性材料本構特性的認識尚不夠全面,降低了人們通過斷裂分析對裂尖形貌的掌握精度,難以準確指導實際的工程設計.

本文主要從體積變化、變形模式、變形程度3個不同角度,對超彈性材料本構關系研究的最新進展進行總結和分析,并對實際超彈性材料完全本構關系建立和可壓超彈性材料應變能函數構造等方面的研究工作提出建議.

1 超彈性材料本構關系研究的基本理論

超彈性材料是一類具有大變形能力的非線性彈性材料,其本構特性完全取決于它的應變能函數[1,8],因而,超彈性材料性能的研究就是運用恰當的理論和方法確定該材料的應變能函數W.

根據連續介質理論,超彈性材料的應變能函數必須遵守“確定性、局部作用性及標架無關性”3 個基本原則[9].此外,作為規范化條件,應變能函數及在可壓情形下表示的應力在未變形的參考構型中還應為零(本文研究以假定無初始應力和應變為前提)[7].另外,在小變形情形下超彈性理論與線彈性理論的自洽性也是一個必須遵守的條件.

為使線彈性材料應變能函數具有正定性,應變能函數需滿足C(classical)條件[10],即線彈性材料的剪切模量G和體積模量K均為正,或剪切模量G為正、泊松比的取值范圍為-1 ＜ν ＜0.5.類似地,超彈性材料應變能函數也需滿足一些附加約束條件,但由于其非線性,這些約束條件表現為多種不同形式,例如:C 條件、B-E (Baker-Ericksen)條件、E (empirical)條件、C-N (Coleman-Noll) 條件、O-F (ordered-force)條件[9]、P-C(pressure compression)條件[11]、Drucker穩定性準則[12]等.需要指出的是,在特殊變形模式下某些條件是等同的,例如等體積變形時P-C 條件與B-E 條件等同[13];在某些材料的某些變形范圍,某些條件甚至不妥,例如,E 條件對于生物聚合物是一種過度約束,B-E 條件在中等到大應變時則是不正確的[9].多個領域的研究人員都研究了應變能函數應滿足的條件,但遺憾地發現,除確定性、局部作用性及標架無關性3 個基本原則以及規范化等基本條件外,其他對超彈性材料應變能函數的附加約束條件都不是基本的,其合理性仍值得商榷[7,14].

根據超彈性材料應變能函數的3 個基本原則,應變能函數應表示為變形張量不變量I1、I2和I3=J2的函數W=W1(I1,I2,J),例如Rivlin 類[15],或表示為3 個主軸方向的主伸縮比λ1,λ2和λ3的函數W=W2(λ1,λ2,λ3),例如Ogden 類[16].

未變形時3 個不變量的值為I1=3,I2=3 和J=1,3 個主伸長比的值為λ1=λ2=λ3=1,這樣,參考構型中無應變能的規范化條件可表示為

可壓材料參考構型中無應力的規范化條件可表示為[17]

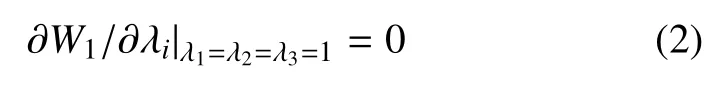
用不變量表示即為

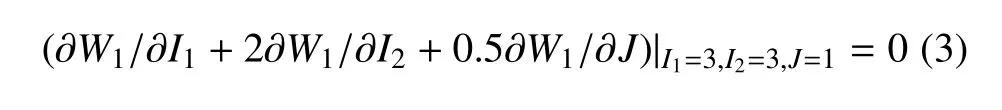
超彈性材料的拉伸模量、剪切模量、體積模量及泊松比等材料參數代表了變形過程中的材料特性.

在單軸拉伸變形模式下,超彈性材料的拉伸模量和泊松比可分別定義(除了本文采用的切線方式定義模量外,非線性材料還可采用割線方式定義模量)為E(λ1)=dT1/dλ1和ν(λ1)=-dλ2/dλ1,其中以應變能函數表示的單軸應力為[18]

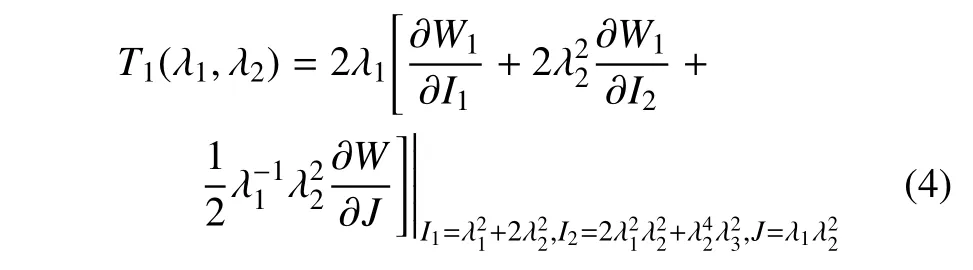
并且,另外兩個方向的主應力為零,即

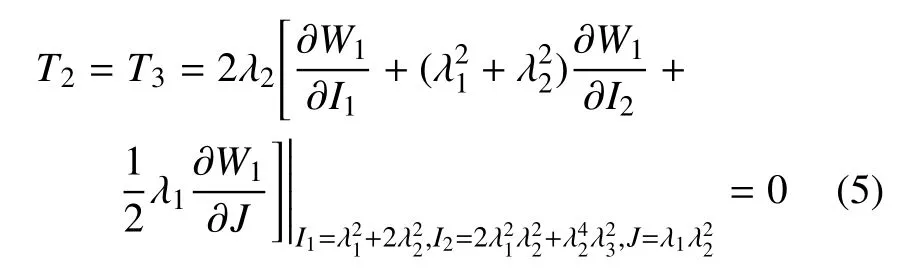
在簡單剪切變形模式下,剪切模量可定義為G(γ)=dT12/dγ,其中應變能函數表示的剪應力為

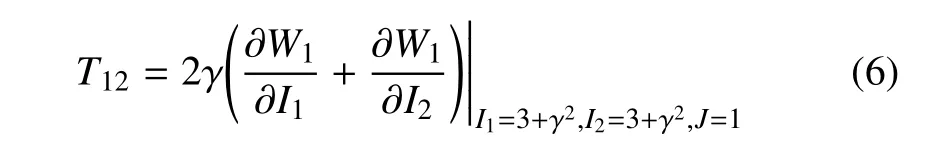
在純體積變形模式下,體積模量可定義為K(J)=dTm/dJ,其中以應變能函數表示的靜水應力為

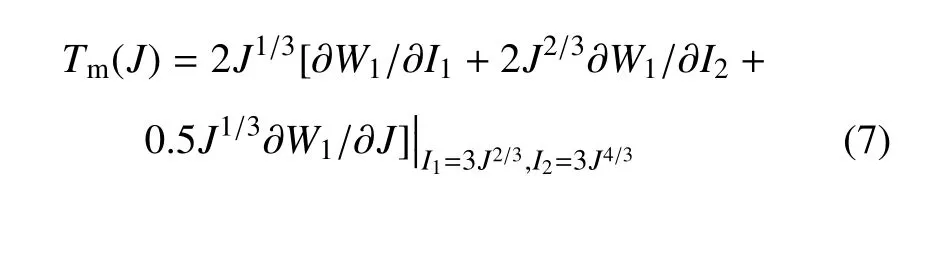
應變能函數在微小變形時需與線彈性理論自洽[13],其含義為微小變形時超彈性材料具有與Hooke線彈性材料相同的物理性質[17],一般表現為如下兩個特性:一個是微小剪切量γ 時的剪切模量G(0)與線彈性材料剪切模量 ˉG具有相同的性質; 另一個微小純體積變形時的體積模量K(1)與線彈性材料體積模量ˉK具有相同的性質.事實上,由于各向同性線彈性材料只具有兩個獨立的材料參數,以單軸應力作用下微小變形時的拉伸模量替代靜水應力作用下純體積變形時的體積模量,將在表述具體模型自洽性條件時更為簡捷,也可利用更易于實現的簡單拉伸實驗測試數據.

由于非線性問題的復雜性及多樣性,這些材料參數常常表現出與線彈性參數迥異的性態.例如,剪切模量不能僅通過單軸拉伸實驗通過拉伸模量和泊松比來得到,需通過剪切實驗測量[13];在描述體積變形時,體積模量與泊松比不再完全等效,而是前者更為恰當[11].采用Hencky 應變時泊松比為常數0.5,才反映不可壓超彈性材料的體積變化特征[13]; 大多材料小變形時的泊松比值在0 與0.5 之間[19],但大變形時軟木塞在軸向壓縮時的表觀泊松比卻為少見的負值[20]; 某些木材徑向伸長、橫向收縮時的表觀泊松比甚至達到0.6～0.8[21],超出了線彈性理論泊松比值最大為0.5 的上限.最近,Sanborn 和Song[22]實驗研究發現,在壓縮變形模式下,硅泡沫材料的泊松比從普通的可壓值轉變為近不可壓值,但準靜態和動態時又略有不同.

研究超彈性材料應變能函數形式的方法主要有兩種[23]:第一種是根據研究者自己的假設,運用基本理論,確定函數的具體形式,例如選取Rivlin 展開式[15]中的前幾項,這是一種“先確定后識別” 的方法;另一種是以實驗數據為依據,根據不同變形模式和/或不同變形范圍時實驗曲線的變化特征,選取相應函數形式,例如Rivlin 和Saunders[24]及Treloar[25]的工作,這是一種“邊確定邊識別”的方法.

具體超彈性材料的應變能函數模型分為數學模型和物理模型兩類:運用連續介質理論,結合超彈性材料的基本條件,推演得到含模型常數的數學模型,再將其應用于材料試驗測試結果,對模型常數加以識別,最終建立超彈性材料的本構關系[16,26].根據超彈性材料的分子鏈結構特征,運用統計力學方法,得到含微觀結構常數的物理模型.以不變量表示應變能函數時,兩種模型對簡單情形得到的形式相同[5],但參數的意義不同:例如neo-Hookean 型超彈性材料,其數學模型的應變能函數為W1=μ(I1-3)/2,模型常數μ 在物理上可解釋為微小變形時的剪切模量G(0)[16];物理模型的應變能函數為W1=nkθ(I1-3)/2,除Boltzmann 常數k和絕對溫度θ 外,唯一的材料參數n具有分子鏈密度[5]的物理含義.數學模型可根據實驗測試數據進行調整,以反映非線性的多樣性;物理模型則可對變形機制給予物理解釋,例如應變能函數中I1的高階項反映了網絡伸長行為的非高斯分布特性[27-28].由于與微觀分子結構建立了物理關聯,物理模型常常含有較少的材料常數,例如三鏈模型[29]、四鏈模型[30]、八鏈模型[31]和全網模型[32-33]均只含有兩個材料參數.特別地,基于微觀結構統計方法的物理模型為描述更復雜變形模式和更大變形范圍給予了啟發和指導[5].研究表明[6],結合數學模型和物理模型,運用協同多尺度方法,可建立更符合具體超彈性材料的本構模型.

總之,由于非線性超彈性材料性能及其表征的復雜性和多樣性,建立本構模型時需要考慮6 方面因素[23].

(1)基本理論:本構模型必須符合理論所要求的3 個基本原則及規范化要求.

(2)附加約束:本構模型及其參數需要滿足某些附加約束條件.

(3)變形模式:由于本構參數與變形模式有關,根據一種實驗數據確定的本構參數,只適用于該類變形模式或被理論證明的等效變形模式,因而,本構模型還需適用于多種變形模式[9].

(4)變形范圍:由于不同變形階段的物理機理不同、變形規律差異較大,本構模型必須適用于理論上允許的整個變形范圍,換句話說,只適用于小變形和中等變形的模型,不適合被用來進行變形很大的裂尖場分析.

(5) 函數形式相對簡單,參數盡可能少:為便于實際應用,本構模型應選用含有較少參數的函數形式,在小變形時保持與線彈性模型自洽,盡管從實驗數據角度這種較簡單模型的預測效果并不是最佳[34];實際上,具有更多參數的復雜模型,有時反而造成對實驗數據的過度擬合[35].

(6)參數具有明確的物理意義:若采用物理模型,其中的常數本身就具有物理意義; 若采用數學模型,其中的常數應通過規范化條件等賦予其物理意義.這是力學方式區別于數學方式研究本構模型的一個顯著特征.

2 研究現狀

2.1 不可壓與可壓本構關系研究

2.1.1 不可壓本構關系研究現狀

實驗表明,大多超彈性材料具有體積變化非常小的特征[26],加之不可壓條件極大簡化了超彈性材料性能的理論研究及工程應用,因而,對不可壓型超彈性材料應變能函數的研究是一項基本而重要的工作.

物理上,材料不可壓時的形狀改變由構型熵變化弓起[5],此時體積比J=1,只有不變量I1和I2是最基本的.目前已提出許多不可壓型應變能函數,文獻[23]的附錄中列出了其中的29 種.

總體而言,不可壓超彈性材料應變能函數的研究有3 個突破性工作.

第一個突破是基于Mooney[36]和Rivlin[14]早期工作建立的Mooney-Rivlin 類模型,是一類數學模型,其形式為[37]

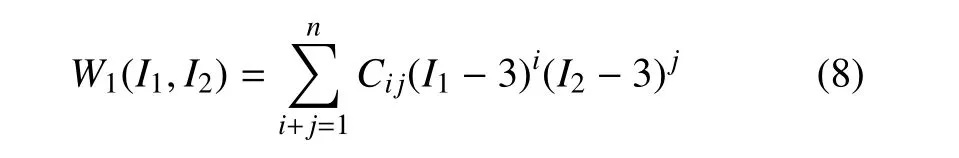
式中,Cij是模型常數.

這類模型以第一變形張量不變量I1和第二變形張量不變量I2的級數形式表示,是基于連續介質理論、運用張量代數表示的超彈性非線性理論,可較好描述小變形和中等程度大變形的超彈性本構關系,是迄今描述各向同性超彈性材料本構關系較為常用的模型[38].這類工作還包括Yeoh 模型[39]、Gent-Thomas模型[40]以及Carroll 模型[26]等.最近,Liu 等[41]在neo-Hookean 模型基礎上提出了一種四參數膠原纖維卷曲本構模型,由于考慮了卷曲度和膠原纖維分散系數的影響,可更好表征角膜前中央基質以及其他生物軟組織的超彈性力學性能.

第二個突破是Ogden 類模型,也是一類數學模型,其形式為[16]

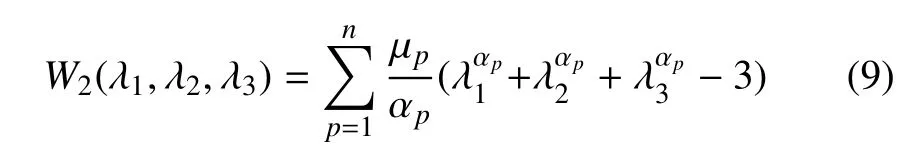
式中,μp與αp是模型常數.

這類模型采用Valanis-Landel 假設[42],以主伸縮比λi表示應變能函數,首次在理論上實現了對多個變形模式、較大應變范圍實驗曲線的準確預測,被認為是非線性彈性建模方面的重要進展[6].

第三個突破是運用基于分子網絡結構的細觀統計力學途徑獲得的應變能函數,是一類物理模型,其形式以不變量或主伸縮比表示.例如Gent 模型[43]及由此而發展的Gent-Gent 模型[44],其形式分別為

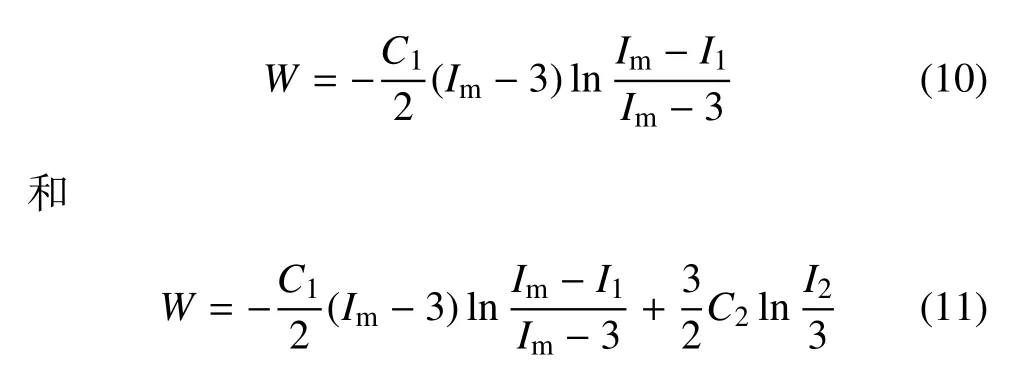
式中,C1和C2為普通模型常數,Im是分子鏈結構極限伸長參數.

可以看出,物理模型都具有參數少的優點,但也可含有缺乏物理意義的模型常數,反映了物理模型的另一方面重要應用.

2.1.2 可壓本構關系研究現狀

諸如橡膠等超彈性材料,雖然一般認為不可壓,但實際上只是近不可壓的,準確的本構模型需要考慮其體積可壓性;在受約束條件下,即使很小的體積變化,對材料的響應都將產生重要影響[5];在多孔固體的大變形過程中,常常伴隨明顯的體積變化,本構模型必須具有描述體積改變的能力.另外,運用有限元方法模擬超彈性材料復雜變形時,可壓材料模型更加自然,可避免不可壓模型對不可壓約束的額外處理[45-46]; 常見的線彈性材料都具有明顯的體積變化特征(線彈性材料的泊松比一般在0.3 左右),只有可壓超彈性材料模型才能成為小變形線彈性模型在大變形方面的自然延伸.這些都表明,計及體積變化的可壓超彈性材料本構關系,理論上才更完善、工程應用中也才更準確.

物理上,超彈性材料的體積改變由內能變化所弓起[5].但為了利用已有不可壓本構關系的研究成果,可壓超彈性材料應變能函數一般通過解除不可壓約束J=1 予以建立[5],據此,可壓模型可分為兩類.

第一類模型是將不可壓應變能函數理解為與體積變形無關的等積(偏量) 應變能,再添加僅與體積比J有關的體積(靜水)應變能部分[23],其形式為

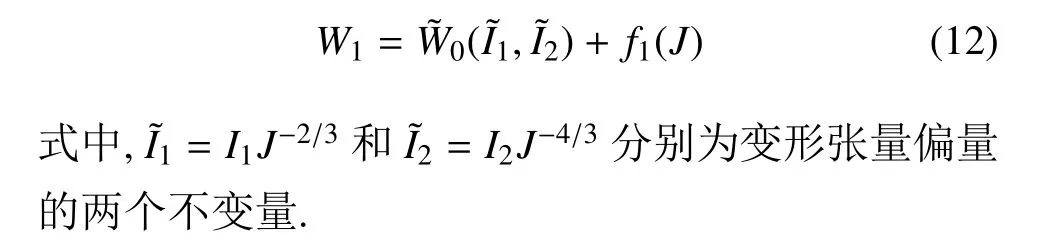
第二類模型是將不可壓應變能函數理解為體積比J→1 時的極限應變能部分,再添加僅與體積比J有關的應變能部分,其形式為

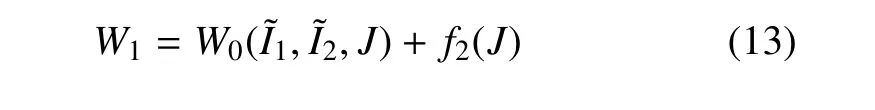
對于靜水壓力狀態,式(12) 描述的體積變化特征為

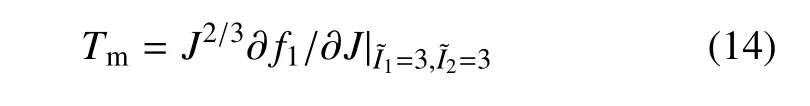
式(13)描述的體積變化特征則為

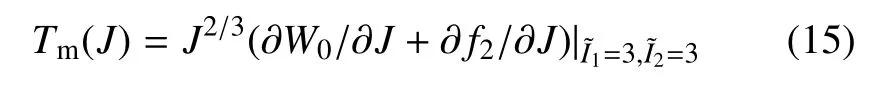
式(15) 表明,式(13) 第二類可壓模型的兩部分都與體積變形有關;另外,通過體積模量與剪切模量的比值變大,該模型可很好模擬材料的近不可壓特性[5].

第一類可壓模型的典型代表是Flory 模型[47]和可壓Mooney-Rivlin 模型,其應變能函數分別為

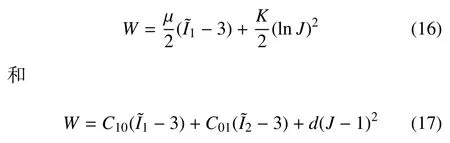
Kumar 和Rao[48]依據式(8) 的一般Mooney-Rivlin 模型進行了可壓本構關系研究,分析了項數對材料本構關系的影響,發現項數增多使得應力應變曲線的拐點增多,C01值的大小影響應力應變曲線的非線性程度.

Blatz 和Ko[49]根據唯象連續介質理論提出的模型是第二類可壓模型的典型代表,其應變能函數可表示為

式中,f∈[0,1]在模型中是一個比例參數,β=ν/(1-2ν)是與泊松比有關的材料常數.

式(18)的Blatz-Ko 模型已廣泛用于模擬多孔材料等可壓各向同性非線性固體,在微小變形時可退化為如下的Gent-Thomas 模型[40,50]

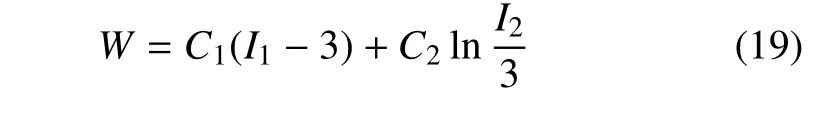
St Venant-Kirchhoff模型[1]可歸為式(13) 取f2(J)=0 的特殊情形,因而也具有描述材料可壓行為的能力; 進一步研究表明[51],因I2項系數為負值而不滿足多凸性附加條件,該模型在一定變形范圍時將產生體積比J為負的非物理結果.

可壓模型的建立需要對體積變形的實驗測試,然而,這方面只有早前的少量報道.例如,Penn[52]及Fong 和Penn[53]采用膨脹儀測試了單軸拉伸過程中的體積改變,雖只得到了相對較小變形時的數據,但觀察到了體積改變增大率隨伸縮比增大而減小的規律.Adams 和Gibson[54]與Bridgman[55]分別開展了天然樹膠的靜水壓縮實驗,將試件置于帶有活塞的圓柱型流體槽中,通過移動活塞壓縮流體,改變試件所受壓力.實驗結果表明,對于相對較大的體積變化(例如J=0.8),材料的壓力隨體積變化呈高度非線性,為體積應變能函數形式的構造提供了依據.

式(12)第一類可壓型應變能函數的加和分解在運用有限元方法進行變形分析時具有優勢,但這種分解只是一種假設,并不是變形(或變形梯度) 張量極分解的必然結果,無小體積變化約束時會造成試件“拉伸時變厚、壓縮時變薄”等非物理的大變形行為[45].Ogden[56]曾建議在第一類可壓模型中再弓入等積和體積兩部分耦合的第三部分應變能,然而,耦合項的存在喪失了本構關系中應力張量和彈性張量可分離的優勢,更增加了確定耦合項參數的困難.

2.2 全變形范圍本構關系研究

超彈性材料的隨機取向分子鏈網絡結構,使其具有承受較大變形的能力,例如Treloar 對硫化橡膠的單軸拉伸實驗,軸向伸長比λ 達到了7.6[25].但是,不是所有本構模型,都能夠很好地描述從小變形到中等變形、再到較大變形的完整變形過程.如圖1 所示,對于氯丁二烯橡膠的大變形,基于交聯聚合物鏈統計熱力學得到的neo-Hookean 模型只適用于初始線性范圍的橡膠類材料[57],三階Ogden 模型比簡單的neo-Hookean 模型則更加適合[58].

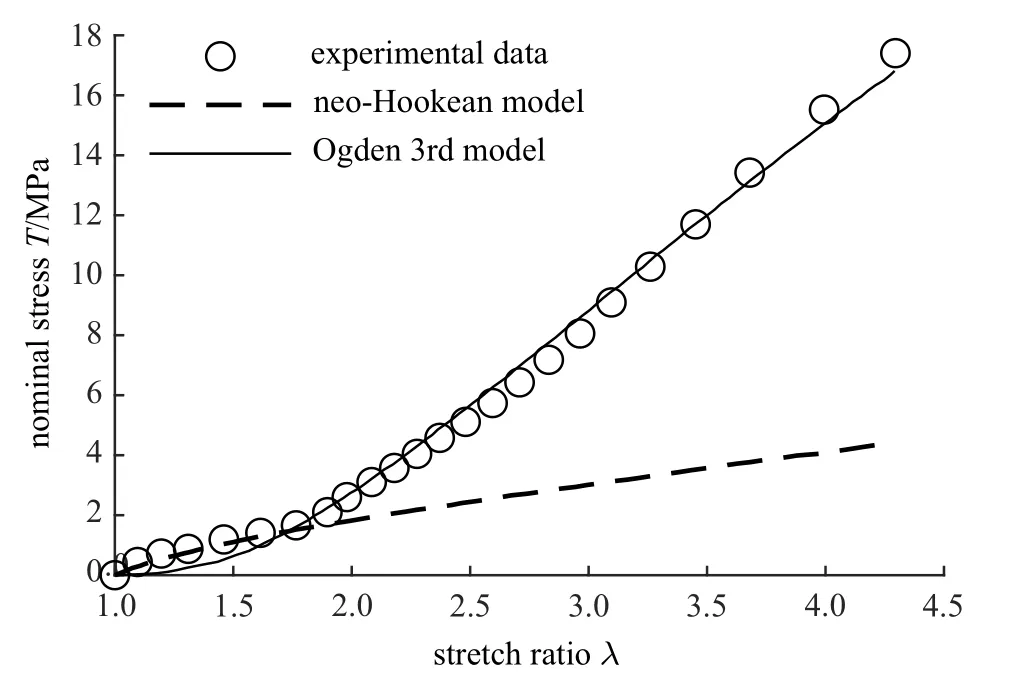
圖1 neo-Hookean 模型和三階Ogden 模型對氯丁二烯橡膠大變形的適用性[58]Fig.1 Applicability of neo-Hookean model and Ogden 3rd model for Chloroprene rubber[58]

Destrade 等[7]的定量工作表明,對于小到中等變形階段,應變能函數W必須是兩個不變量I1和I2的函數,排除了Yeoh 模型等W=W(I1)型廣義neo-Hookean 類模型用于中等變形階段的可能; Mooney-Rivlin[37]、Gent-Thomas[40]和Carroll[26]三種不同模型由于都含有兩個不變量,它們對這兩個變形階段(例如1 ≤λ ＜4)都能進行很好預測,如圖2 所示.鑒于得到了不依賴應變能函數具體形式的結論,該工作被認為是超彈性材料本構關系研究方面的一項重要工作.

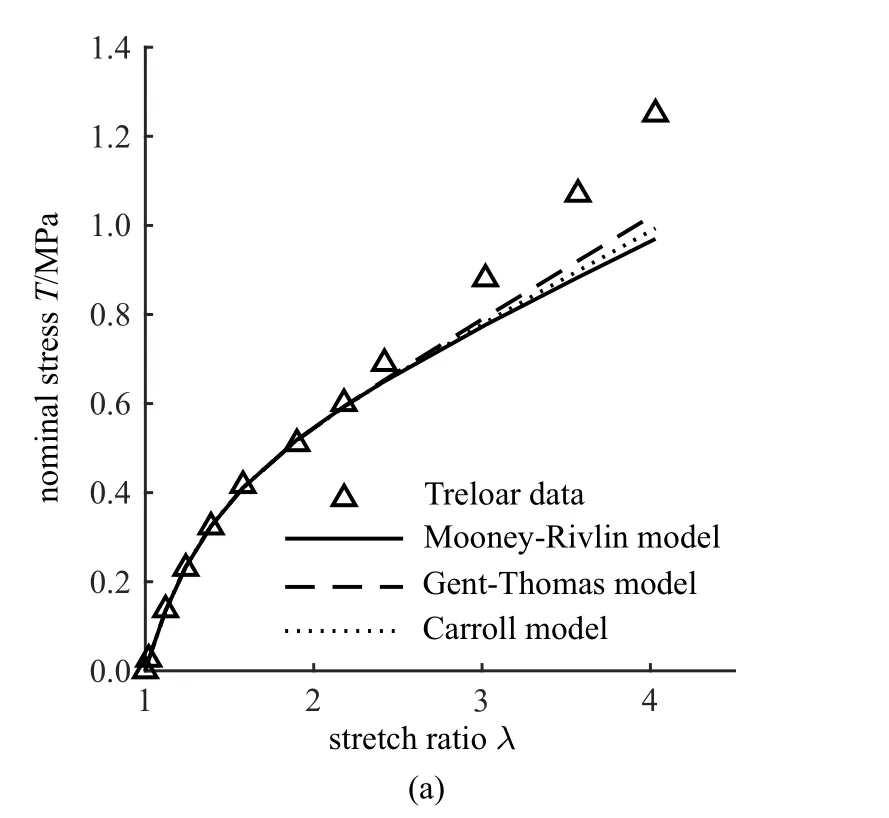
圖2 W=W(I1,I2)型應變能函數對不同變形階段的預測效果[7]Fig.2 Predictions of strain energy functions described by W=W(I1,I2)for different deformation regions[7]

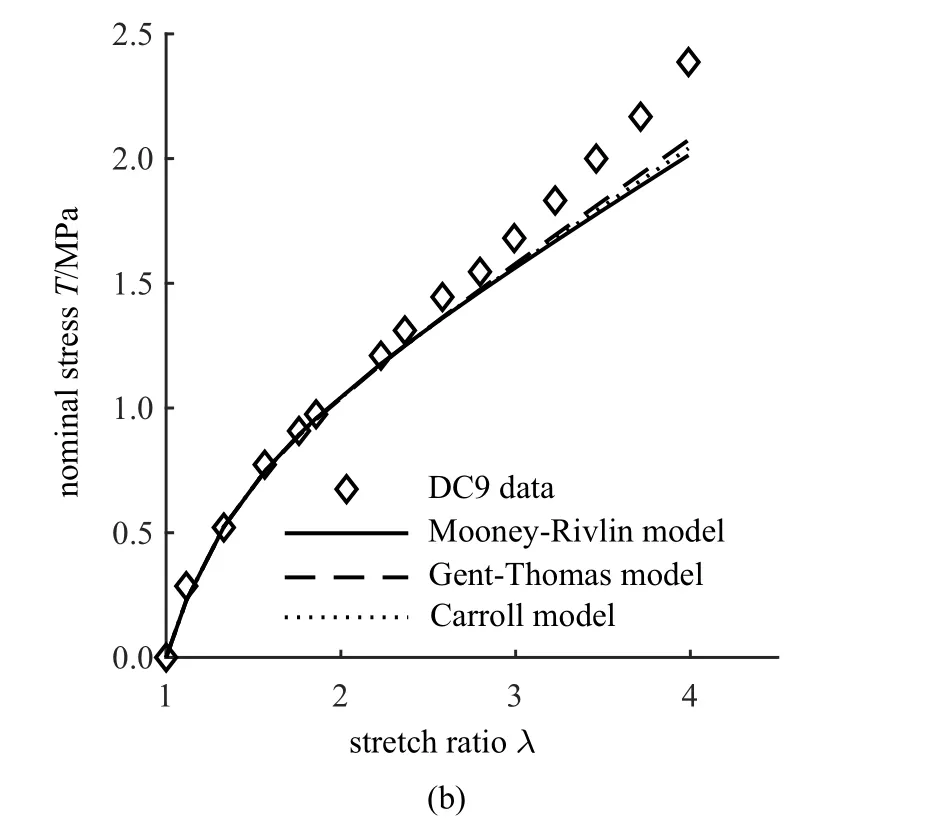
圖2 W=W(I1,I2)型應變能函數對不同變形階段的預測效果[7](續)Fig.2 Predictions of strain energy functions described by W=W(I1,I2)for different deformation regions[7](continued)

建立能描述全變形范圍拉伸實驗的本構模型,需要與實際實驗曲線相結合的建模步驟.Destrade等[7]還對實驗數據進行了Mooney 圖變換g(z)–z,即橫軸運用伸縮比的倒數z=1/λ、縱軸運用折算應力g(z).這樣,如圖3 所示,整個拉伸曲線被劃分為變形機制不同的3 個階段:第一階段是小到中等變形階段,此時聚合物鏈容易展開,Mooney 圖幾乎為直線.第二階段是應變硬化階段,此時成束鏈團的展開使得材料的剛度增加,表現為Mooney 圖中曲線的“向上翻轉”.第三階段是分子鏈的極限伸長階段,隨著分子鏈拉伸至其極限,材料出現了劇烈的剛化現象.三個階段的特征分別通過不同的函數形式在應變能函數中予以反映,最終得到的應變能函數為

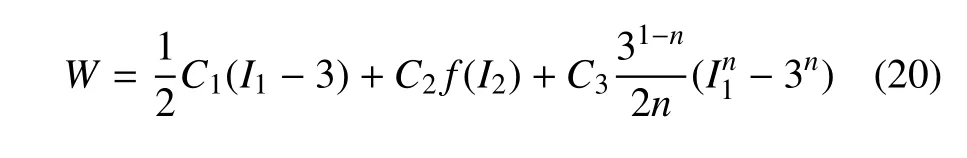
式中,C1,C2,C3與n均為模型常數.

式(20) 對實驗數據的全變形范圍能很好擬合,在統計力學框架內還可給出物理解釋,是數學模型與物理模型相結合開展超彈性材料全變形范圍非線性本構關系研究的典型案例.對Treloar[25]經典實驗數據及Dobrynin 和Carrillo[59]數據的分析結果表明,Pucci 和Saccomandi[44]提出的三參數Gent-Gent 模型能表征橡膠類非線性彈性材料完整變形過程,五參數Carillo-Dobryin 模型也是一種很好的選擇,并通過預測簡單剪切實驗對這兩個模型的強健性進行了驗證.

圖3 典型拉伸實驗數據的Mooney 圖變換[7]Fig.3 Mooney plots of typical uniaxial tension’s data[7]

同樣基于Treloar 的單軸拉伸數據,Beda[23]通過對整個變形過程進行分級和漸進式增加高階項的做法,提出逐步分析法,研究全變形范圍的不可壓超彈性材料的應變能函數.由于只有實驗數據與前一步模型預測的偏差在增加項預測時起作用,因此新增加項不影響在前一步已很好預測的變形階段,從而轉化成非線性優化問題并加以求解,得到的應變能函數為

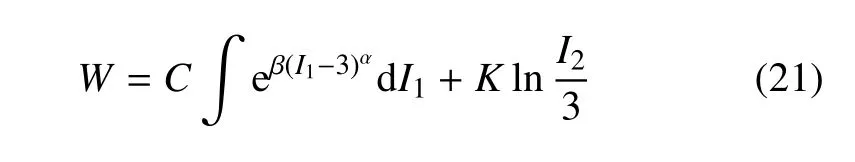
式中,C,K,α 和β 為模型常數.

式(21) 推廣了Hart-Smith 模型[60],并再次證實了第二不變量I2在應變能函數中的關鍵作用.

依據小變形到中等變形、再到大變形的全變形范圍的單軸拉伸實驗,學者們開展了卓有成效的研究工作,得到了式(20) 和式(21) 等全新形式的本構模型,它們更符合具體材料的實驗曲線特征.

2.3 多種變形模式本構關系研究

單軸拉伸的實驗測試和理論研究固然非常基本和重要,但實際問題的變形場往往是復雜多樣的,多種不同的變形模式同時存在,因而,本構關系的研究還應考慮對單軸拉伸以外其他多種變形模式的適用性.不可壓各向同性材料一般具有3 對共6 種均勻變形模式,即單軸拉伸與等雙軸壓縮、單軸壓縮與等雙軸拉伸以及純剪切與面內壓縮[9].因此,每對中各取其一的單軸拉伸、單軸壓縮及純剪切3 種變形模式被稱為基本變形模式.在材料試驗中,最常見的變形模式為單軸或雙軸拉伸[34],較少見的是簡單剪切或純剪切以及扭轉[61],更少見的則是復合剪-拉或復合扭-拉[62],能包含3 種基本變形模式的完整的材料實驗并不多見.

研究應變能函數對多種變形模式的適用性,考察不同變形模式時模型常數的差異,是超彈性材料本構關系研究的一項重要工作.Ogden[16]研究表明,neo-Hookean 模型僅能描述橡膠在小到中等程度的剪切變形,但增加了I2的Mooney–Rivlin 模型其適應性可明顯改善,對橡膠特性的預測與實驗數據更吻合[6].雖尚不能從理論上解釋neo-Hookean 模型和Mooney-Rivlin 模型產生差異的原因,但實例分析表明[24,63],為了適應更多不同的變形模式,應變能函數都需包含第二不變量I2.

Carroll[26]詳細分析了3 組典型的實驗數據,即Treloar[25]給出的簡單拉伸、純剪切、復合剪-拉以及等雙軸拉伸的數據,Rivlin 和Saunders[24]給出的簡單拉伸、純剪切以及復合剪-拉數據及一個主變量不變而其他主變量變化等多種實驗數據,以及Jones和Treloar[64]給出的面內一個主伸長不變、另一個變化的實驗數據.基于其共有的“曲線形狀不變性”[42],他提出了建立本構模型的3 步驟方法:第一步用neo-Hookean 模型進行模擬,識別參數,使neo-Hookean 模型在一定變形范圍內(例如1 ＜λ ＜4.5)對Treloar 的拉伸數據能夠準確模擬; 第二步建立變形范圍修正模型,計算neo-Hookean 模型對更大變形范圍Treloar拉伸實驗數據預測的應力殘差,藉此提出變形范圍修正模型并識別其參數; 第三步建立模式修正模型,計算前兩步所得模型對Treloar 等雙軸拉伸這一不同變形模式實驗預測的應力殘差,藉此提出模式修正模型并識別其參數.最終,通過3 步分別得到的應變能函數的加和,得到可適用于多種變形模式的應變能函數為

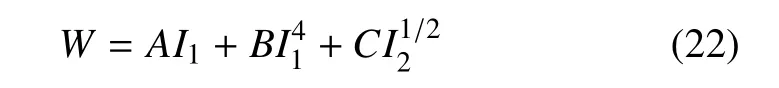
式中,A,B和C為模型常數.該模型對實際多種變形模式的預測效果如圖4 所示.

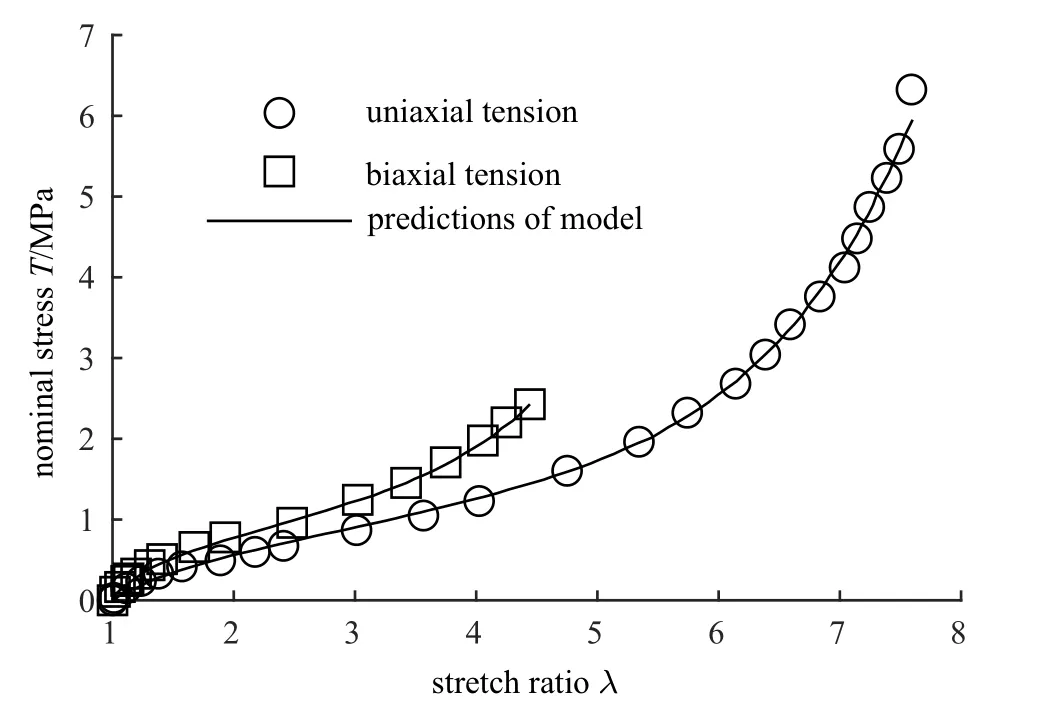
圖4 式(22)對Treloar 的單軸拉伸和等雙軸拉伸兩種模式實驗結果的預測效果[26]Fig.4 The predictions of Eq.(22)for Treloar’s uniaxial tension and biaxial tension[26]

利用Gent[43]弓入的分子鏈結構極限伸長參數Im,并通過新增項,Carroll[65]新近對Treloar 等雙軸拉伸全變形范圍的實驗數據進行了很好擬合,得到了可同時適用于拉伸和等雙軸拉伸模式的全變形范圍的應變能函數為

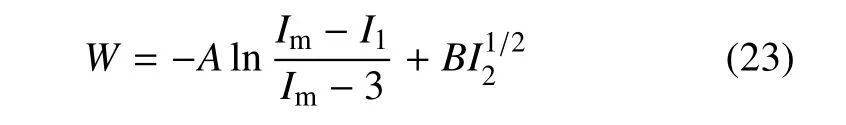
式(22) 和式(23) 在函數形式上非常接近,這一有趣現象表明,從宏觀實驗數據角度,采用式(21)的數學模型和式(22) 的物理模型,都可獲得適合多變形模式的超彈性材料本構關系.

3 研究展望

實際上,從物理學觀點,超彈性材料本構關系必須是普遍的,雖不苛求其能夠描述所有超彈性材料的力學行為,但要求其能夠描述某種具體材料多種變形模式下全變形范圍的非線性力學特性,因而,對不同變形模式及不同變形范圍的適用性是超彈性材料本構關系研究的重要課題,同時也是本構關系在斷裂分析等超彈性材料實際應用中迫切需要解決的根本問題[7].

3.1 完全本構關系研究

依據等雙軸拉伸實驗數據,Carroll[26,65]研究了其全變形范圍的本構關系,與單軸拉伸相比,變形模式中涵蓋了等雙軸拉伸,雖然還只是一種等效的單向壓縮模式; 同時研究了單軸拉伸、純剪切及復合剪-拉3 種多種變形模式,但變形范圍又相對較小(λ ＜4).因而,仍需開展超彈性材料的建模方法研究,以建立適用于多種變形模式、能描述全變形范圍的超彈性材料的完全本構關系.

3.1.1 多變形模式本構關系

研究發現,應變能函數的具體形式對其描述能力及有限元數值實現將產生重要影響[7].對于非線性材料,根據一種變形模式所建立的本構模型對其他變形模式可能效果很差、甚至不適用[9].

筆者認為,以小到中等變形范圍(例如單軸拉伸時1 ≤λ ≤3)的實驗數據為對象,可通過“賦初始模型-增加修正項-多模式驗證”的研究步驟,開展多變形模式本構關系研究:第一步賦初始模型,即以某模型(例如neo-Hookean 模型或Mooney-Rivlin 模型)為初始模型,以單軸拉伸(基本變形模式) 實驗數據進行參數識別;第二步增加修正項,即針對另一典型(例如等雙軸拉伸或剪切)變形模式,根據初始模型的預測差異,結合相關數學模型或相應變形機制的物理模型,確定修正項函數,進行參數識別;第三步進行多模式驗證,即將模型用于其他變形模式,驗證對更多變形模式的適用性,確認模型的強健性.

多變形模式本構關系,適用于小到中等變形范圍的超彈性材料的復雜響應分析,但對裂尖區變形很大的斷裂問題分析仍不適用.

3.1.2 完全本構關系

超彈性材料的單軸拉伸實驗曲線一般都有一個明顯的大變形階段,例如Treloar 單軸拉伸實驗的伸長比λ 達7.6,對應工程應變超600%,因而,全變形范圍本構模型不僅具有理論研究意義,而且具有實際應用價值.

將多模式本構關系延伸至全變形范圍,可建立超彈性材料的完全本構關系:以較大變形程度(例如單軸拉伸時λ ＞3) 的拉伸實驗為依據,以多變形模式本構關系為初始模型,運用“賦初始模型-增加修正項-多模式驗證”的研究步驟,構造應變能函數,建立超彈性材料的完全本構關系.

理論上,完全本構關系完整描述了超彈性材料的非線性特性,可應用于所有情形的力學響應分析,包括實際結構的復雜應力場問題和裂紋尖端的大變形場問題.

3.2 不可壓與可壓本構關系的相關性研究

由于不可壓材料的實驗數據最為豐富,3.1 節展望了不可壓完全本構關系的研究.實際的超彈性材料一般只是近不可壓的,可壓超彈性材料本構模型在理論上更一般,在微小體積變形時還可退化為不可壓模型,因而,研究可壓超彈性材料的完全本構關系在力學理論和工程應用上都具有重要意義.

對于超彈性材料,首先研究較簡單的不可壓型本構關系,再經擴充發展成為可壓型本構關系,符合人類的認知過程;從科學研究的角度,從更一般的可壓型本構關系出發,通過不可壓條件進行退化,可揭示材料不可壓特性的物理機制.事實上,一種簡單的不可壓模型會通過性能差異很大的多個不同的復雜可壓模型退化而來,單從不可壓模型難以追溯得到材料自身獨特的可壓或近不可壓特性.所以,不可壓與可壓本構關系的相關性問題是一個嚴肅的科學問題.

以硫化橡膠材料為例,Fong 和Penn[53]進行了單軸拉伸實驗研究,同時獲得了拉伸應力與伸長比的關系曲線和體積比與伸長比的關系曲線.他們運用兩項不可壓Mooney-Rivlin 模型,取應變能函數為

通過對拉伸應力與伸長比關系曲線擬合,得到模型常數為C10=0.181 MPa 和C01=0.082 MPa.

根據與線彈性理論的自洽性,由式(24) 得到該材料的初始剪切模量為=2(C10+C01)=0.526 MPa.

若依式(12) 建立形如式(17) 的第一類可壓Mooney-Rivlin 模型,通過對拉伸應力與伸長比關系曲線和體積比與伸長比關系曲線同時進行擬合,Horgan 和Murphy[46]得到式(17)中的模型常數為C10=0.092 MPa,C01=0.237 MPa 和d=1000.1 MPa.

根據與線彈性理論的自洽性,由式(17) 得到該材料的初始剪切模量為=2(C10+C01)=0.658 MPa,初始體積模量=2d=2000.2 MPa,進而得到初始泊松比ν=0.4998.與式(24)不可壓模型相比,初始剪切模量相差25.1%.

若依式(13) 建立第二類可壓Mooney-Rivlin 模型,其應變能函數取為

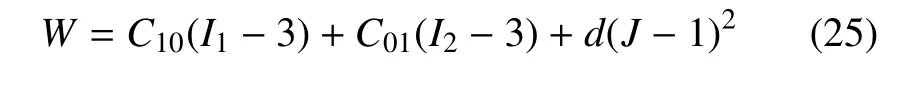
通過對拉伸應力與伸長比關系曲線和體積比與伸長比關系曲線同時進行擬合,在相關系數R2=0.998 6時,可得到式(25)中的模型常數為C10=0.307 MPa,C01=-0.157 MPa 和d=1605.4 MPa.

根據與線彈性理論的自洽性,由式(25) 得到該材料的初始剪切模量為=2(C10+C01)=0.300 MPa,初始體積模量=2d-8(C10+C01)/3=1605 MPa,進而得到初始泊松比ν=0.499 9.與式(24)不可壓模型相比,初始剪切模量相差達43.0%.

上述兩種可壓模型,雖然都得到了接近于0.5 的近不可壓初始泊松比,但由于C10和C01兩個與不可壓特性密切相關的模型常數值差異較大、甚至發生了正負號變更,可以說不能退化為相應的不可壓Mooney-Rivlin 模型,特別是,關鍵的初始剪切模量相差懸殊.

為此,在建立可壓超彈性模型時,應當根據不可壓模型已得到的模型常數,進一步構造體積變化影響項.

本小節的初步分析表明,對于超彈性材料,從不可壓本構到可壓本構的延拓,仍有一些值得研究的新問題.

4 結論

近一百年、特別是第二次世界大戰結束之后的七十余年來,對超彈性材料的性能研究已經取得了豐碩成果,在科學研究和工程應用的多個方面得到了應用.然而,模型的多樣性及差異性從側面折射出人們對目前狀況的不滿足及該問題研究的開放性.

超彈性材料性能理論研究和實際應用的最基礎問題是真實而完整的本構關系研究,雖已提出超30種(類)模型,但仍有很大的發展空間.本文對超彈性材料本構關系的基本理論、發展史上的重要進展及目前的最新成果進行了梳理,分析了超彈性材料完全本構關系研究的理論價值和工程意義,對超彈性材料性能的進一步研究及其他非線性材料性能的研究也大有裨益.