坐標基準間的坐標轉換

丁愛民 （安慶市勘察測繪院，安徽 安慶 246000）

0 前言

坐標基準是測繪工作的空間起算依據(jù)，不僅為空間地理信息描述提供起算原點和起算面，也是確定空間地理信息的幾何形態(tài)和時空分布規(guī)律的基礎。坐標系統(tǒng)之間的差異主要來自于坐標系統(tǒng)的定義不同，具體表現(xiàn)為坐標系原點、坐標軸指向和尺度因子的差異。目前常用的坐標系統(tǒng)有2000國家大地坐標系、1980西安坐標系和1954北京坐標系。

隨著2000國家大地坐標系（CGCS2000）的實施，將有多源、多尺度的海量空間地理信息數(shù)據(jù)需要統(tǒng)一到新的測繪基準，以滿足城市建設和管理對測繪地理信息產品的需求。在將現(xiàn)有成果轉換至CGCS2000的具體實踐中，眾多學者對三維七參數(shù)法、平面四參數(shù)法等坐標轉換方法開展了深入研究，而針對不同區(qū)域、不同坐標轉換模型的適用性分析不夠。因此，研究一種滿足一定精度要求的轉換方法，實現(xiàn)不同參考橢球基準下的坐標轉換，對實際工作具有指導意義。

1 坐標轉換原理與方法

坐標轉換包括坐標系轉換和坐標基準轉換。坐標系轉換是基于同一參考橢球下的不同表現(xiàn)形式的坐標轉換，如空間直角坐標（X，Y，Z）與大地坐標（大地緯度B，大地經度L，大地高H）的相互轉換、高斯平面直角坐標（X，Y）與大地坐標（B，L）的相互轉換；坐標基準轉換是基于不同參考橢球下的坐標轉換，如不同空間直角坐標系的轉換、不同大地坐標系的轉換和不同平面坐標系的轉換。根據(jù)轉換形式，又可分為二維坐標轉換和三維坐標轉換。常用的坐標轉換模型有基于空間坐標的布爾莎模型、基于大地坐標的三維七參數(shù)模型、基于平面坐標的平面四參數(shù)模型等。

不同坐標系坐標轉換的實現(xiàn)是根據(jù)同時擁有兩種坐標系坐標的大地點（重合點）的條件下，選擇適當?shù)闹睾宵c，利用所選重合點兩種坐標系的坐標，采用適當?shù)淖鴺宿D換模型，運用最小二乘法計算坐標轉換參數(shù)，再通過坐標回代求得所求坐標系的坐標。

坐標轉換通常有兩種方法：一是整體轉換法，整個區(qū)域計算一套轉換參數(shù)；二是分區(qū)轉換法，當轉換區(qū)域較大時，為保證轉換精度，將整個轉換區(qū)域劃分成若干個分區(qū)，分別對各分區(qū)計算轉換參數(shù)。在計算各分區(qū)轉換參數(shù)時，為了保持各分區(qū)在接邊處轉換參數(shù)的連續(xù)性，需要各分區(qū)之間相互重疊一部分重合點并重復使用以求取轉換參數(shù)。

坐標轉換的精度除取決于坐標轉換的數(shù)學模型和求解轉換參數(shù)的重合點坐標精度外，還與重合點的數(shù)量、幾何形狀結構有關。為滿足規(guī)范要求，必須選取高等級、高精度且分布均勻的點作為坐標轉換的重合點；重合點的分布要覆蓋整個轉換區(qū)域且盡量分布均勻，特別要注意轉換區(qū)域周邊覆蓋；重合點的數(shù)量不得少于5個。同時應對參與解算轉換參數(shù)的重合點進行準確分析、篩選、試算，剔除大于3倍中誤差的粗差點，采用不含粗差且具有一定密度的重合點解算轉換參數(shù)，直到滿足精度要求為止。評定轉換參數(shù)的精度包括內符合精度和外符合精度，用參與參數(shù)計算的重合點坐標殘差計算內符合精度，選擇部分未參與參數(shù)計算的重合點作為外部檢核點，用轉換參數(shù)計算這些點的坐標與已知坐標比較進行外部檢核，得到坐標殘差計算外符合精度。用于檢核坐標轉換精度的外部檢核點不應少于6個。

2 坐標轉換模型

2.1 布爾莎模型（三維七參數(shù)）

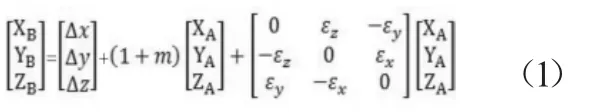
式中：（XAYAZA）T為某點在空間直角坐標系A的坐標，（XBYBZB）T為該點在空間直角坐標系B的坐標，（Δx Δy Δz）T為3個平移參數(shù)；（εxεvεz）T為3個旋轉參數(shù)；m為尺度變化參數(shù)。

該模型中含有7個轉換參數(shù)，為了求得這7個參數(shù)，至少需要3個重合點，當多于3個重合點時，可按最小二乘法求得7個參數(shù)的最或是值。

2.2 平面四參數(shù)模型（二維四參數(shù)）

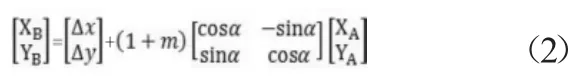
式中：2 個平移參數(shù) Δx、Δy，1 個旋轉參數(shù)α和1個尺度變化參數(shù)m。

采用平面四參數(shù)模型共有4個轉換參數(shù)，至少需要2個重合點，當多于2個重合點時，可按最小二乘法求得4個參數(shù)的最或是值。

2.3 轉換參數(shù)精度評定

坐標轉換精度是通過求取轉換參數(shù)的重合點的殘差中誤差體現(xiàn)的。轉換精度依據(jù)下式計算：

對轉換參數(shù)進行精度的檢驗、評定主要包括以下兩個方面：參與參數(shù)計算的重合點的內符合精度；未參與參數(shù)計算的外部檢核點的外符合精度。

3 工程案例

將安慶市1954年北京坐標系成果轉換到CGCS2000國家大地坐標系，使用工具軟件為安慶市2000國家大地坐標系轉換軟件，其功能主要分為7大模塊，包括坐標轉換參數(shù)求解、設置轉換參數(shù)、DLG數(shù)據(jù)轉換、DEM數(shù)據(jù)轉換、DOM數(shù)據(jù)轉換、字符串格式數(shù)據(jù)轉換和常用軟件包（高斯投影正反算（X，Y）與（B，L）相互轉換；3°、6°、任意帶投影換帶計算；空間大地坐標（B，L，H）與空間直角坐標（X，Y，Z）相互轉換）。該軟件支持1954年北京坐標系、1980西安坐標系、CGCS2000坐標系之間的相互轉換；支持多種轉換方法，包括平面四參數(shù)、三維七參數(shù)、布爾莎三維七參數(shù)等；支持點數(shù)據(jù)、圖形數(shù)據(jù)等對象以及多種數(shù)據(jù)格式的文件。

3.1 轉換精度分析

①設置計算轉換參數(shù)的重合點相鄰點對平均間距10km，選取市域125個C級和D級GPS點以及224個實測CGCS2000坐標的特征點作外部檢核，分別采用布爾莎模型和平面四參數(shù)模型進行試算求取轉換殘差，統(tǒng)計按兩種模型得到的平面坐標分量殘差及點位中誤差（單位m）分布區(qū)間，并進行對比分析。

采用布爾莎模型轉換：平面坐標x分量轉換精度為0.008m，平面坐標y分量轉換精度為0.009m，平面點位中誤差0.012m。平面坐標x分量殘差絕對值最大值0.061m，平面坐標y分量殘差絕對值最大值0.043m。平面點位中誤差最大值為0.055m。平面點位中誤差分布見圖1。

采用平面四參數(shù)模型轉換：平面坐標x分量轉換精度為0.013m，平面坐標y分量轉換精度為0.008m，平面點位中誤差0.015m。平面坐標x分量殘差絕對值最大值0.019m，平面坐標y分量殘差絕對值最大值0.019m。平面點位中誤差最大值為0.027m。平面點位中誤差分布見圖2。

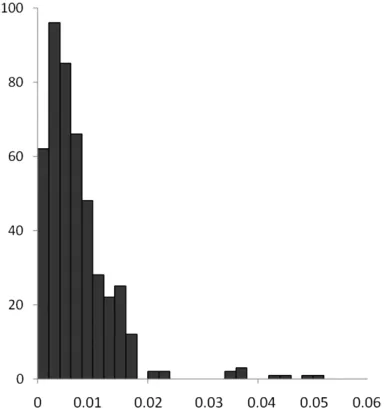
圖1 布爾莎模型（10km）平面點位中誤差分布直方圖

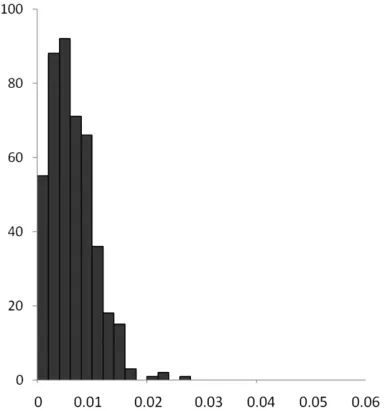
圖2 平面四參數(shù)模型（10km）平面點位中誤差分布直方圖

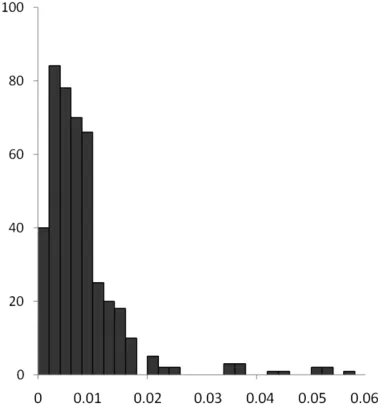
圖3 布爾莎模型（15km）平面點位中誤差分布直方圖

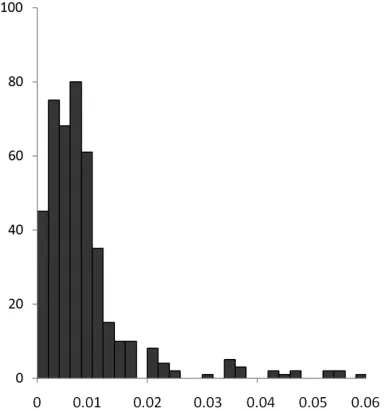
圖5 布爾莎模型（20km）平面點位中誤差分布直方圖

②設置計算轉換參數(shù)的重合點相鄰點對平均間距分別為15km、20km時，按兩種模型計算轉換殘差得到的平面點位中誤差分布見圖3～圖6。

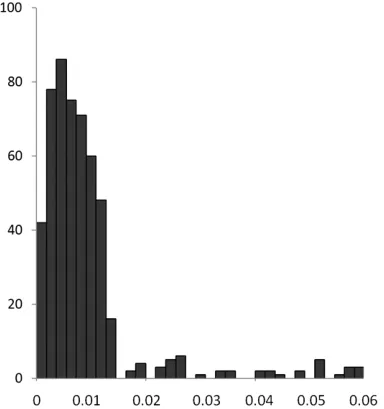
圖6 平面四參數(shù)模型（20km）平面點位中誤差分布直方圖

從平面點位中誤差分布直方圖可以看出，99%的轉換誤差分布在3倍中誤差以內，小于圖上0.1mm，個別山地轉換精度大于5cm，主要集中在偏離中央子午線較遠的山地，但是不影響整體轉換精度評價。

隨著轉換區(qū)域的增大，采用布爾莎模型轉換精度變化不大，而平面四參數(shù)模型轉換精度衰減顯著，其原因是投影變形所致。

3.2 分析結論

①平面四參數(shù)模型屬平面坐標系間的二維相似變換，未考慮橢球曲面影響，適用于投影變形小的局部區(qū)域坐標轉換。其轉換精度能夠滿足1∶500比例尺的圖形轉換，布爾莎模型是空間直角坐標系間基于不同橢球的三維轉換，適用于較大區(qū)域的坐標轉換，其轉換精度能夠滿足1∶1000比例尺及更小的圖形轉換。

②當轉換區(qū)域較大時，為保證必要的轉換精度，坐標轉換可采取兩種方法，一是劃分轉換區(qū)域分別轉換，二是在三維七參數(shù)模型中增加橢球長半軸和扁率變化參數(shù)進行約束。

4 結語

坐標基準轉換是不同橢球間的坐標轉換。在實際應用中，要綜合考慮待轉換的兩個坐標系的基本信息、轉換區(qū)域與地圖投影中央子午線的距離、區(qū)域大小、重合點的數(shù)量及分布等情況，選擇適宜的坐標轉換模型，對重合點的選擇方案以及轉換模型進行反復驗證，確定轉換參數(shù)，提高坐標轉換精度。