最小二乘無網(wǎng)格方法及其在近空間解體碎片繞流場(chǎng)模擬應(yīng)用

羅萬清，梁劍寒，李海燕，李志輝，3*

(1. 國(guó)防科技大學(xué)高超聲速?zèng)_壓發(fā)動(dòng)機(jī)技術(shù)重點(diǎn)實(shí)驗(yàn)室，長(zhǎng)沙410073； 2. 中國(guó)空氣動(dòng)力研究與發(fā)展中心超高速空氣動(dòng)力研究所，綿陽621000；3. 國(guó)家計(jì)算流體力學(xué)實(shí)驗(yàn)室，北京100191)

1 引言

空間碎片是指在發(fā)射火箭、衛(wèi)星等飛行器執(zhí)行太空任務(wù)后產(chǎn)生的火箭箭體、衛(wèi)星本體以及航天器在軌執(zhí)行航天任務(wù)過程中產(chǎn)生的拋棄物、太空中物體之間碰撞產(chǎn)生的碎塊等。 特別是諸如天宮一號(hào)目標(biāo)飛行器超期服役兩年半突發(fā)功能失效，面臨無控飛行、軌道衰降、再入墜毀，飛行航跡預(yù)示，大部解體會(huì)在再入環(huán)境強(qiáng)氣動(dòng)力/熱作用下熔融/燒蝕，至少10%～40%的殘骸碎片墜落地面[1]。 為此，發(fā)展準(zhǔn)確求解近空間多次解體非規(guī)則殘骸碎片間繞流干擾問題的數(shù)值計(jì)算方法[2]，成為數(shù)值預(yù)報(bào)落區(qū)散布范圍的重要途徑。

數(shù)值方法種類很多，如有限差分法、有限體積法、有限元法以及譜離散法等，這些方法在模擬流動(dòng)時(shí)首先對(duì)流動(dòng)區(qū)域進(jìn)行網(wǎng)格離散，然后將需要求解的流動(dòng)方程在空間網(wǎng)格上進(jìn)行離散，進(jìn)而求解得到流動(dòng)區(qū)域內(nèi)的流場(chǎng)參數(shù)[3-4]。 基于此，空間離散網(wǎng)格對(duì)計(jì)算效率和結(jié)果可靠性有重大影響，在網(wǎng)格生成時(shí)不得不同時(shí)考慮網(wǎng)格數(shù)量、網(wǎng)格正交性、疏密分布等。 由于在實(shí)際工程問題中存在大量具有復(fù)雜幾何外形的流動(dòng)，如航天器再入近空間多次解體非規(guī)則殘骸碎片間繞流相互干擾，或者具有運(yùn)動(dòng)邊界的復(fù)雜流動(dòng)，既計(jì)算高效又保證結(jié)果準(zhǔn)確地求解這些復(fù)雜問題至今仍是計(jì)算流體力學(xué)的難點(diǎn)[5]。無網(wǎng)格方法采用基于點(diǎn)的近似原理，只需要空間節(jié)點(diǎn)信息，不需要將節(jié)點(diǎn)連接成網(wǎng)格單元，與使用網(wǎng)格的傳統(tǒng)算法相比，可以徹底或部分地脫離網(wǎng)格，適合于復(fù)雜外形流場(chǎng)的計(jì)算[4]。 發(fā)展無網(wǎng)格方法求解流動(dòng)控制方程是解決傳統(tǒng)數(shù)值模擬方法網(wǎng)格生成瓶頸問題的一種新嘗試。

經(jīng)過多年的發(fā)展，無網(wǎng)格方法已成功應(yīng)用于材料動(dòng)力學(xué)、結(jié)構(gòu)動(dòng)力學(xué)等領(lǐng)域，在航天器解體、空間碎片防護(hù)等領(lǐng)域展現(xiàn)出了很好的應(yīng)用前景[6-10]。 Batina[11]首先將無網(wǎng)格方法應(yīng)用于計(jì)算流體力學(xué)，發(fā)展了用于求解氣體流動(dòng)問題的無網(wǎng)格方法。 O?ate 和Ortega 等[12-14]先后將所發(fā)展的無網(wǎng)格數(shù)值方法成功用于求解對(duì)流擴(kuò)散問題、不可 壓 流 動(dòng)、 可 壓 縮 流 動(dòng)、 勢(shì) 流 等 問 題。 Katz等[15-16]將無網(wǎng)格方法用于重疊網(wǎng)格之間的信息交換，開展了無網(wǎng)格體積法(Meshless volume scheme)和多重點(diǎn)云(Multicloud)方法的研究。 此外，國(guó)外還有很多學(xué)者開展了與求解氣體流動(dòng)的無網(wǎng)格方法相關(guān)的通量格式、隱式方法、性能比較分析以及結(jié)合笛卡爾網(wǎng)格等方面的研究[17-20]。國(guó)內(nèi)將無網(wǎng)格方法運(yùn)用于計(jì)算流體力學(xué)的研究起步較晚。 陳紅全等[21-22]和葉正寅等[23-24]較早開展了該領(lǐng)域研究。 近年來，陳紅全研究團(tuán)隊(duì)和譚俊杰、許厚謙等研究團(tuán)隊(duì)開展了大量采用無網(wǎng)格方法數(shù)值求解氣體流動(dòng)問題的研究，包括無網(wǎng)格與笛卡爾網(wǎng)格混合算法[25-26]、無網(wǎng)格方法誤差分析[27]、無網(wǎng)格方法求解非定常問題[28-30]等相關(guān)領(lǐng)域。

早期無網(wǎng)格方法研究中，求解無粘通量多采用添加人工耗散的中心差分格式。 該法具有形式簡(jiǎn)單、計(jì)算效率高等優(yōu)勢(shì)，但在耗散項(xiàng)中引入了經(jīng)驗(yàn)參數(shù)，針對(duì)不同問題需要對(duì)參數(shù)進(jìn)行人為調(diào)整，且很難推廣應(yīng)用到高超聲速流動(dòng)甚至非平衡流動(dòng)的模擬。 由于對(duì)通量格式魯棒性的要求更高，模擬非平衡流動(dòng)時(shí)，傳統(tǒng)網(wǎng)格法多采用矢通量分裂格式，其中Steger-Warming(SW)格式得到廣泛應(yīng)用[31-36]。 在求解氣體流動(dòng)的無網(wǎng)格方法研究中，尚未見采用SW 格式求解無粘通量的報(bào)道。

本文以無粘Euler 方程為研究對(duì)象，推導(dǎo)適于無網(wǎng)格方法的SW 通量格式，建立求解二維無粘氣體流動(dòng)的最小二乘無網(wǎng)格方法，并通過二維翼型、帶斜面管道流動(dòng)以及類解體碎片圓柱繞流干擾問題等典型算例對(duì)方法進(jìn)行驗(yàn)證。 由于碰撞或壽命末期大型航天器解體后，會(huì)產(chǎn)生大量碎片，相互之間會(huì)產(chǎn)生干擾，進(jìn)而影響其氣動(dòng)特性和飛行航跡。 本文以串列和并列雙圓柱作為航天器多次解體殘骸碎片簡(jiǎn)化模型，采用建立的無網(wǎng)格數(shù)值方法分析圓柱間距對(duì)碎片流場(chǎng)特性的影響。

2 無網(wǎng)格方法計(jì)算原理

無網(wǎng)格方法基本思想是基于空間離散點(diǎn)，在局部計(jì)算域內(nèi)按一定法則構(gòu)造一系列點(diǎn)云，求解區(qū)域用點(diǎn)云離散代替網(wǎng)格單元，點(diǎn)云由中間的中心點(diǎn)和周圍的衛(wèi)星點(diǎn)組成，在點(diǎn)云上通過特定方法構(gòu)建空間導(dǎo)數(shù)的近似表達(dá)式，進(jìn)而對(duì)流動(dòng)控制方程求解，通過更新計(jì)算域內(nèi)離散點(diǎn)處的流場(chǎng)信息，擺脫對(duì)離散網(wǎng)格的依賴，因此在求解諸如航天器解體殘骸碎片等復(fù)雜非規(guī)則外形繞流時(shí)更具靈活性。 常見求解氣體流動(dòng)問題的無網(wǎng)格方法有基于泰勒展開的最小二乘法(TLS)、基于多項(xiàng)式展開的最小二乘法(PLS)和徑向基函數(shù)(RBF)法等[4，6-12]，本文采用TLS 對(duì)流場(chǎng)進(jìn)行模擬。

在二維局部域上構(gòu)建點(diǎn)云結(jié)構(gòu)，即確定中心點(diǎn)和衛(wèi)星點(diǎn)，如圖1 所示，假設(shè)i 為點(diǎn)云中心點(diǎn)，j為其衛(wèi)星點(diǎn)(共m 個(gè))。 為了降低點(diǎn)云結(jié)構(gòu)中衛(wèi)星點(diǎn)距中心點(diǎn)距離對(duì)空間導(dǎo)數(shù)求解精度的影響，需要引入權(quán)函數(shù)，且權(quán)函數(shù)應(yīng)在數(shù)學(xué)上滿足單調(diào)性、緊支性、正定性等條件[4]。

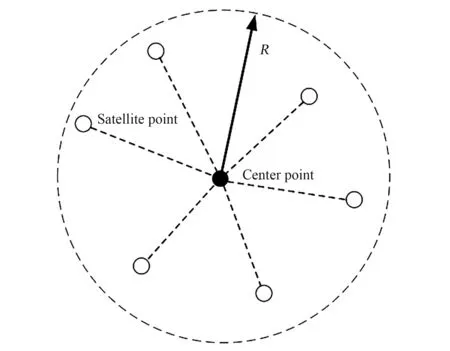
圖1 點(diǎn)云結(jié)構(gòu)Fig.1 Cloud of points

衛(wèi)星點(diǎn)上的任意流場(chǎng)參數(shù)φ 按泰勒級(jí)數(shù)展開，可由中心點(diǎn)的參數(shù)近似表達(dá)，見式(1):

在中心點(diǎn)為i 的點(diǎn)云結(jié)構(gòu)上建立如下總體誤差函數(shù)，見式(2):

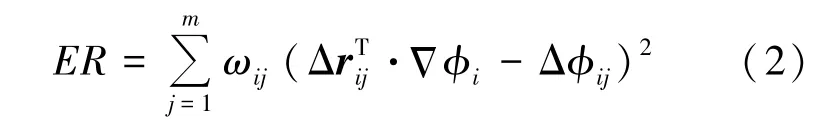
為了使式(2)的總體誤差達(dá)到最小，采用最小二乘法可獲得流場(chǎng)參數(shù)空間導(dǎo)數(shù)的表達(dá)式如式(4)所示:

式中，最小二乘系數(shù)aij、bij只與點(diǎn)云結(jié)構(gòu)中的離散點(diǎn)位置坐標(biāo)有關(guān)，如果求解過程中點(diǎn)云結(jié)構(gòu)不發(fā)生變化，則系數(shù)可以在迭代之前保存，無需參與迭代。

3 數(shù)值方法

3.1 流動(dòng)控制方程

笛卡爾坐標(biāo)系下的二維完全氣體流動(dòng)控制方程表達(dá)如式(5)所示:

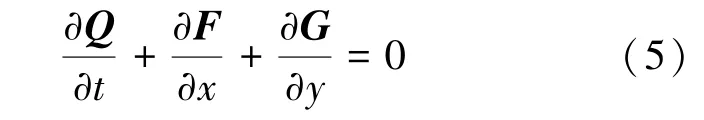
式中，Q 為守恒變量，t 為時(shí)間，F(xiàn)、G 分別為x、y 方向的無粘通量，如式(6)所示:

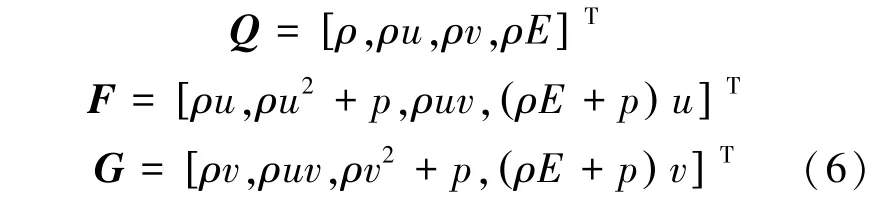
式中，ρ、p、E 分別表示氣體密度、壓力和單位質(zhì)量總能，u、v 分別表示x、y 方向的速度分量。

3.2 空間離散

通過最小二乘法獲得空間導(dǎo)數(shù)的基礎(chǔ)上，空間點(diǎn)i 上的流動(dòng)控制方程可寫成式(7):

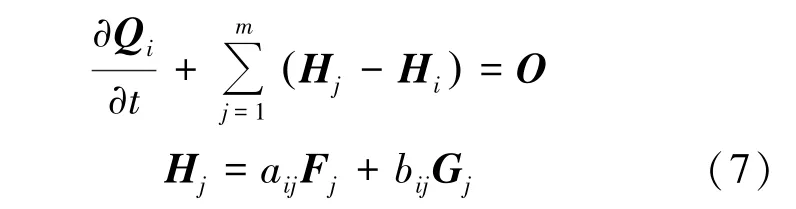
或式(8):

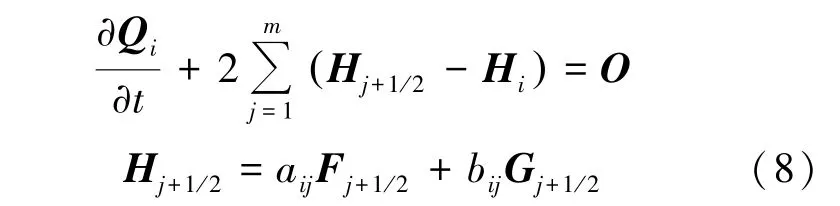
式中，下標(biāo)j ＋1/2 代表點(diǎn)云的中心點(diǎn)i 到衛(wèi)星點(diǎn)j 連線半點(diǎn)上的參數(shù)。 求解式(7)或(8)，即可得流場(chǎng)參數(shù)。 采用中心差分格式時(shí)，主要采用端點(diǎn)表達(dá)形式，而采用SW 格式等迎風(fēng)格式時(shí)，則采用半點(diǎn)表達(dá)形式，方便重構(gòu)以提高求解精度。

3.3 SW 通量格式

與傳統(tǒng)網(wǎng)格法不同，式(7)或(8)中多出了在中心點(diǎn)的通量項(xiàng)Hi，該項(xiàng)直接采用中心點(diǎn)參數(shù)獲得，而在中心點(diǎn)i 與衛(wèi)星點(diǎn)j 連線的半點(diǎn)上，則和網(wǎng)格法一樣需要對(duì)變量進(jìn)行重構(gòu)以提高求解精度，同時(shí)需要添加斜率限制器防止振蕩[37]。

采用添加min mod 限制器的MUSCL 重構(gòu)方法，無粘通量基于重構(gòu)原始變量的SW 分裂表達(dá)式見式(9):

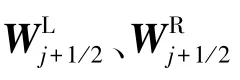
半點(diǎn)上原始變量重構(gòu)差值見式(10):

圖2 半點(diǎn)重構(gòu)示意圖Fig.2 Reconstruction schematic at midpoint

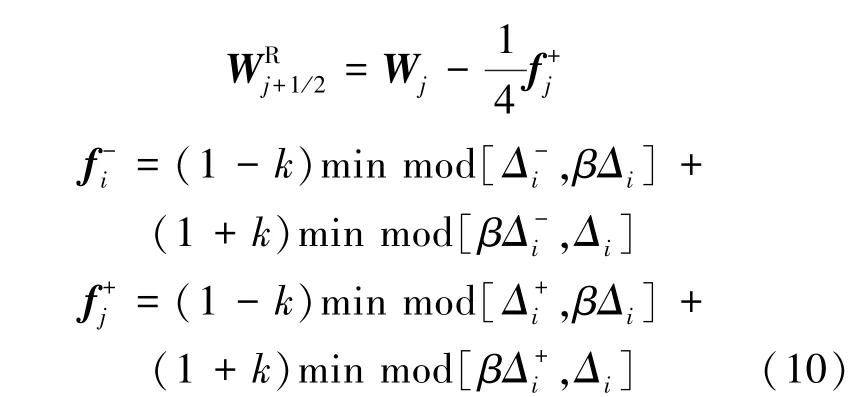
計(jì)算中參數(shù)k 和β 都取1.0，式中差分算子表示見式(11):

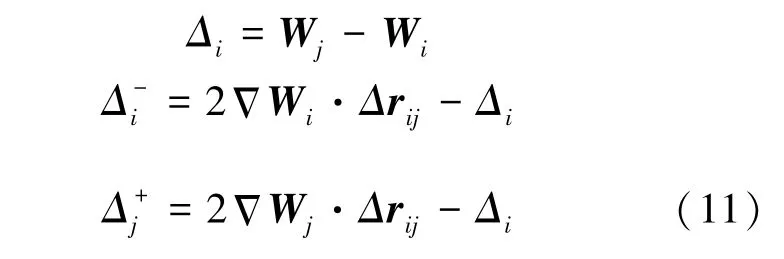
在重構(gòu)變量的基礎(chǔ)上，引入無網(wǎng)格最小二乘系數(shù)，推導(dǎo)得到半點(diǎn)上基于SW 格式的無粘通量分裂后的表達(dá)式為式(12)、(13):

式中，

式中，γ 為氣體比熱比，c 為氣體聲速，λ1、λ2、λ3為通量雅可比矩陣的3 個(gè)特征值，式(12)中正負(fù)特征值定義為式(14):

式中，ε 取一個(gè)極小的正數(shù)，以防止在聲速點(diǎn)附近出現(xiàn)波動(dòng)。

3.4 邊界條件

采用無網(wǎng)格方法求解流動(dòng)控制方程時(shí)，同樣需要給出合適的定解條件，初始條件確定相對(duì)容易，而邊界條件則相對(duì)復(fù)雜，處理不當(dāng)會(huì)降低解的穩(wěn)定性和準(zhǔn)確性。 對(duì)外流而言，主要涉及固壁邊界條件和遠(yuǎn)場(chǎng)邊界條件的數(shù)值處理。

無粘流動(dòng)要求固壁上流動(dòng)滿足無穿透條件，即在固壁上法向速度為0，壓力、密度法向梯度均為0。 首先由邊界點(diǎn)的點(diǎn)云結(jié)構(gòu)中的內(nèi)點(diǎn)衛(wèi)星點(diǎn)通過鏡像獲得虛擬點(diǎn)坐標(biāo)，將虛擬點(diǎn)加入邊界點(diǎn)的點(diǎn)云結(jié)構(gòu)中，通過法向梯度條件獲得虛擬點(diǎn)上的參數(shù)值，再計(jì)算得到固壁邊界點(diǎn)上的參數(shù)，參與流場(chǎng)求解[38]。

設(shè)置遠(yuǎn)場(chǎng)邊界是為了減少有限的計(jì)算區(qū)域?qū)δM結(jié)果的影響，根據(jù)特征化基礎(chǔ)邊界條件確定，須保證向外傳播的擾動(dòng)波不會(huì)被邊界反射到內(nèi)場(chǎng)，處理方法和網(wǎng)格法類似。 若邊界位置流動(dòng)為超聲速，則入口邊界條件直接由上游參數(shù)賦值，所有出口邊界條件均用外插獲得；若流動(dòng)為亞聲速，則通過垂直于邊界的Riemann 不變量獲得邊界點(diǎn)上的流動(dòng)參數(shù)。

3.5 時(shí)間離散推進(jìn)

由式(7)或(8)可得到i 點(diǎn)的Euler 方程半離散形式，如式(15)所示:

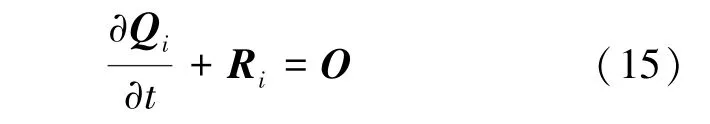
時(shí)間離散推進(jìn)過程采用具有強(qiáng)穩(wěn)定性的三階SSP 型Runge-Kutta 法，由第n 時(shí)間步到第n ＋1時(shí)間步的迭代過程如式(16)所示:

在求解Euler 方程時(shí)，求解時(shí)間步長(zhǎng)Δt 由格式穩(wěn)定性條件決定。 在圖1 所示點(diǎn)云結(jié)構(gòu)中，點(diǎn)云半徑較小的區(qū)域Δt 較小，而在點(diǎn)云半徑較大的區(qū)域Δt 則較大。 對(duì)定常流計(jì)算，只要求得到最終的穩(wěn)態(tài)解，時(shí)間步長(zhǎng)取局部當(dāng)?shù)胤€(wěn)定性條件所允許的最大值，可大大加速整體計(jì)算推進(jìn)過程，縮短計(jì)算時(shí)間[4]。 為此，在迭代過程中，采用局部時(shí)間步長(zhǎng)和殘值光順加速收斂技術(shù)，提高數(shù)值計(jì)算的收斂速度[29，38]。

4 算法驗(yàn)證

4.1 NACA0012 翼型繞流

采用經(jīng)典的NACA0012 翼型跨聲速和超聲速繞流流場(chǎng)算例對(duì)建立的最小二乘無網(wǎng)格數(shù)值方法進(jìn)行驗(yàn)證。 計(jì)算域的遠(yuǎn)場(chǎng)邊界距物面大約為20倍弦長(zhǎng)，流場(chǎng)離散點(diǎn)基于結(jié)構(gòu)網(wǎng)格生成，共有離散點(diǎn)20 307 個(gè)，其中固壁上有133 個(gè)，翼型表面附近區(qū)域空間離散點(diǎn)分布如圖3 所示。 分別模擬來流馬赫數(shù)0.8、迎角1.25°，以及來流馬赫數(shù)1.2、迎角7°兩個(gè)狀態(tài)的跨聲速和超聲速流動(dòng)。

圖3 NACA0012 翼型壁面附近區(qū)域離散點(diǎn)Fig.3 Point distribution around NACA0012 airfoil

圖4 中繪出了NACA0012 翼型跨聲速M(fèi)∞＝0.8，α ＝1.25°繞流流場(chǎng)壓力分布云圖，可以看出采用SW 格式的無網(wǎng)格方法很好地捕捉到了上下表面的激波。 為了更加清晰地比較分析不同方法結(jié)果特點(diǎn)與變化規(guī)律，圖5 將本文無網(wǎng)格方法獲得的該翼型表面壓力系數(shù)與采用AUSM＋-up 格式計(jì)算得到的結(jié)果[24]以及實(shí)驗(yàn)測(cè)量數(shù)據(jù)[26](EXP)進(jìn)行了比較。 可以看出，在激波附近區(qū)域，基于SW 無粘格式的無網(wǎng)格方法并未出現(xiàn)數(shù)值振蕩或數(shù)值過沖，表明該格式具有很好的魯棒性；其余區(qū)域壓力系數(shù)也與實(shí)驗(yàn)測(cè)量值吻合很好，驗(yàn)證了所建立無網(wǎng)格方法模型的可靠性。

圖4 NACA0012 翼型跨聲速流場(chǎng)壓力分布Fig.4 Pressure contours of NACA0012 transonic flow

圖5 NACA0012 翼型跨聲速繞流壁面壓力系數(shù)比較Fig.5 Comparison of surface pressure coefficient distribution in NACA0012 transonic flow

圖6 和圖7 分別繪出了NACA0012 翼型超聲速M(fèi)∞＝1.2、α＝7°繞流流場(chǎng)壓力分布以及壁面壓力系數(shù)的比較情況。 可以看出對(duì)超聲速流動(dòng)而言，采用SW 格式的無網(wǎng)格數(shù)值方法獲得的翼型上下表面壓力系數(shù)與采用其他如Roe 格式文獻(xiàn)計(jì)算結(jié)果[29]以及實(shí)驗(yàn)測(cè)量值[26](EXP)吻合很好，表明發(fā)展的無網(wǎng)格方法模擬二維超聲速流動(dòng)的準(zhǔn)確可靠性。

圖6 NACA0012 翼型超聲速流場(chǎng)壓力分布Fig.6 Pressure contours of NACA 0012 supersonic flow

圖7 NACA0012 翼型超聲速繞流壁面壓力系數(shù)比較Fig.7 Comparison of surface pressure coefficient distribution for NACA0012 supersonic flow

4.2 帶斜面管道流動(dòng)

采用建立的無網(wǎng)格數(shù)值方法模擬如圖8 的超聲速管道流動(dòng)，入口馬赫數(shù)2.0，流場(chǎng)離散點(diǎn)數(shù)目共5781 個(gè)，其中下壁面141 個(gè)。

圖8 管道流動(dòng)結(jié)構(gòu)圖Fig.8 Configuration of the channel flow

通過數(shù)值模擬獲得了管道流動(dòng)流場(chǎng)中的壓力、馬赫數(shù)等參數(shù)分布，從圖9 和圖10 可以看出，流場(chǎng)參數(shù)分布合理，很好地描述了流場(chǎng)結(jié)構(gòu)，包括對(duì)稱面上激波相交與管道壁面上激波反射現(xiàn)象。

根據(jù)來流馬赫數(shù)和尖劈角通過方程(17)可得激波角:

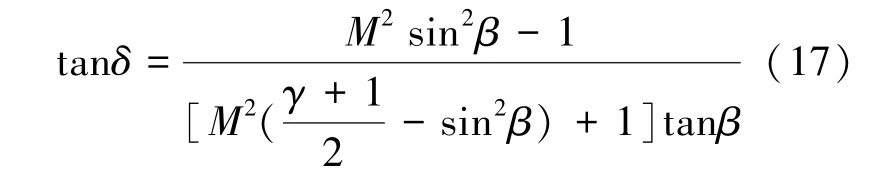
式中，δ 為尖劈角，β 為激波角，γ 為氣體比熱比，M 為來流馬赫數(shù)。

圖9 管道流動(dòng)中的壓力分布Fig.9 Pressure contours for the channel flow

圖10 管道流動(dòng)中的馬赫數(shù)分布Fig.10 Mach number contours for the channel flow

通過迭代可得該流動(dòng)狀態(tài)下管道內(nèi)斜激波的激波角為45.344°，進(jìn)而可以獲得斜激波的準(zhǔn)確位置。 圖11 給出了下壁面和對(duì)稱面上的馬赫數(shù)分布，其中實(shí)心方塊為下壁面上斜激波起始點(diǎn)和對(duì)稱面上激波交叉點(diǎn)，可看出建立的無網(wǎng)格方法較好地捕捉了激波位置。

圖11 管道流動(dòng)邊界上馬赫數(shù)分布Fig.11 Mach number on boundaries of the channel flow

4.3 雙圓柱繞流

為了描述近空間多次解體產(chǎn)生的殘骸碎片間繞流干擾，擬定串列雙圓柱繞流模擬兩殘骸碎片簡(jiǎn)化物繞流流動(dòng)，在空間離散點(diǎn)或網(wǎng)格疏密分布相當(dāng)和通量格式相同的基礎(chǔ)上，與傳統(tǒng)有限體積法進(jìn)行對(duì)比驗(yàn)證，在比較時(shí)采用GLM 代表無網(wǎng)格方法，F(xiàn)VM 代表基于網(wǎng)格的有限體積法。

串列雙圓柱圓心之間的距離為2 倍圓柱直徑，模擬采用的流場(chǎng)空間離散點(diǎn)共有15 299 個(gè)，其中2 個(gè)圓柱壁面上共有128 個(gè)，圓柱附近空間離散點(diǎn)分布如圖12 所示。 模擬狀態(tài)為標(biāo)準(zhǔn)狀況大氣超聲速流動(dòng)，來流馬赫數(shù)為1.5，迎角0°。

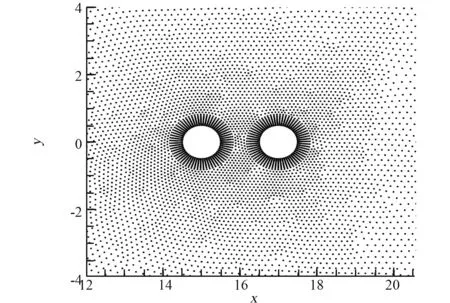
圖12 串列雙圓柱繞流流場(chǎng)離散點(diǎn)分布Fig.12 Point distribution around two cylinders in tandem arrangement

圖13 比較了串列雙圓柱繞流流場(chǎng)密度分布，可看出無網(wǎng)格法和有限體積法得到的流場(chǎng)中脫體激波、膨脹波及尾跡等形狀都比較接近。 圖14 比較了兩圓柱表面壓力分布，絕大部分區(qū)域2 種方法結(jié)果吻合很好，在后駐點(diǎn)附近區(qū)域，無網(wǎng)格方法獲得的壓力略高，可能的原因有待進(jìn)一步分析。

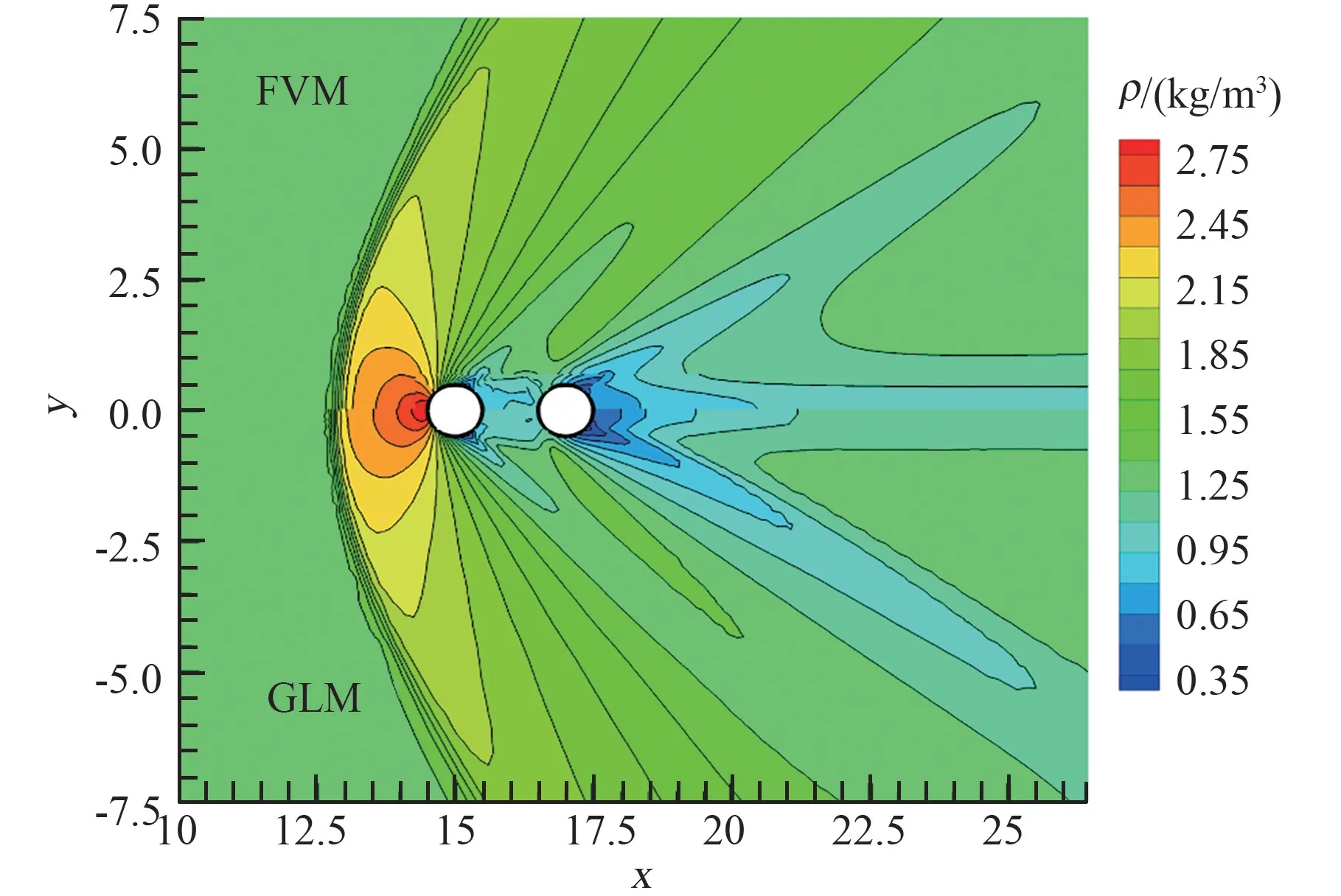
圖13 雙圓柱繞流密度分布比較Fig.13 Comparison of density for the flow over double cylinders

圖14 圓柱表面的壓力分布比較Fig.14 Comparison of surface pressure distribution of cylinders

5 解體碎片流場(chǎng)模擬

以串列雙圓柱和并列雙圓柱作為簡(jiǎn)化的航天器多次解體產(chǎn)生殘骸碎片模型，采用建立的無網(wǎng)格方法對(duì)其繞流干擾流場(chǎng)進(jìn)行模擬，分析碎片間距對(duì)流場(chǎng)特性的影響。 假設(shè)圓柱直徑為D，設(shè)置串列雙圓柱間距分別為2D、4D、8D，模擬高度30 km，飛行速度900 m/s，對(duì)并列雙圓柱間距分別為3D、6D、12D，模擬高度50 km，飛行速度800 m/s。

圖15 給出了不同間距的串列雙圓柱繞流流場(chǎng)壓力分布比較情況。 可以看出，當(dāng)一塊碎片處于另一塊碎片之后時(shí)，由于前面碎片尾流的影響，后面碎片來流速度明顯降低，駐點(diǎn)壓力也會(huì)低于前面碎片，當(dāng)間距很小時(shí)甚至在后面碎片的頭部區(qū)域都不能形成超聲速流場(chǎng)。 這種情況下，后面碎片的升力更小，所以下降比前面碎片要快。 圖16 比較了不同間距的并列雙圓柱繞流流場(chǎng)壓力分布。 對(duì)并列的2 塊碎片，間距很小的時(shí)候存在相互干擾，由于中間壓力增大，碎片運(yùn)動(dòng)會(huì)朝著增大間距的方向發(fā)展，隨著間距的增大，干擾逐漸降低直至消失。 就模擬狀態(tài)而言，當(dāng)并列圓柱之間的間距大于6 倍圓柱直徑時(shí)，二者之間幾乎不再相互干擾。 研究結(jié)果說明碎片間距不同，相互之間流場(chǎng)干擾程度不同，進(jìn)而對(duì)氣動(dòng)特性和飛行航跡的影響程度也不同。

圖15 串列雙圓柱繞流壓力分布比較Fig.15 Comparison of pressure distribution for the flow over two tandem cylinders

圖16 并列雙圓柱繞流壓力分布比較Fig.16 Comparison of pressure distribution for the flow over two side-by-side cylinders

6 結(jié)論

以求解無粘流Euler 方程為目標(biāo)，推導(dǎo)建立了求解二維無粘流動(dòng)的最小二乘無網(wǎng)格數(shù)值方法。 對(duì)典型算例和簡(jiǎn)化碎片模型繞流進(jìn)行了求解，結(jié)論如下:

1) 針對(duì)典型翼型繞流、超聲速管道流動(dòng)和串列雙圓柱繞流等問題，開展無網(wǎng)格數(shù)值方法模擬驗(yàn)證，得到了與實(shí)驗(yàn)數(shù)據(jù)、分析解以及文獻(xiàn)和網(wǎng)格方法計(jì)算結(jié)果間的定量化比較確認(rèn)。 分析表明構(gòu)造設(shè)計(jì)的無網(wǎng)格方法無粘通量格式能夠有效避免數(shù)值振蕩和數(shù)值過沖，對(duì)精細(xì)捕捉基于Euler 方程描述的流場(chǎng)流動(dòng)特征具有很好的收斂適應(yīng)性與可靠性。

2) 以串列雙圓柱和并列雙圓柱作為簡(jiǎn)化模型開展航天器解體碎片超聲速流場(chǎng)數(shù)值模擬，獲得了不同排列方式和不同間距碎片的繞流流場(chǎng)，結(jié)果表明碎片間距增大，相互間的干擾減弱。 同時(shí)說明建立的無網(wǎng)格方法具備推廣至開展近空間非規(guī)則物形粘性流動(dòng)模擬的潛在能力，證實(shí)了算法模型的有效性。

3) 本文工作屬初步階段性，文中算例基于無粘假設(shè)，與真實(shí)流動(dòng)還存在一定差異，更精細(xì)計(jì)算分析需要開展三維粘性流動(dòng)無網(wǎng)格模擬方法。 下一步將圍繞提高無網(wǎng)格方法數(shù)值精度與魯棒性，開展無網(wǎng)格粘性流動(dòng)模擬及無網(wǎng)格自適應(yīng)方法研究，發(fā)展完善適于非規(guī)則物形繞流的無網(wǎng)格數(shù)值方法，并拓展應(yīng)用于航天器多次解體殘骸碎片氣動(dòng)力/熱繞流問題模擬研究。