矩形鋼管混凝土柱貫通隔板弱軸方向傳力研究

費建偉,李志安,楊紅亮,劉飛東,王 群,曹本富,孫忠偉

(浙江中南建設集團鋼結構有限公司，浙江 杭州 310052)

矩形鋼管混凝土柱是指在矩形鋼管中填充混凝土且鋼管及其核心混凝土能共同承受外荷載作用的豎向承重構件[1],它具有強度高、剛度大、延性好和耗能能力強、制作和施工方便、經濟效果好等諸多優點[2-3]。矩形鋼管混凝土結構在高層及超高層建筑中具有很好的應用前景,現已受到國內外工程領域的普遍重視[4]。在多高層建筑中,矩形鋼管混凝土柱通過節點與梁等水平構件連接組成抵御地震作用的抗側力體系,所以鋼管混凝土節點的計算方法和構造措施是應用中必須解決的關鍵問題[5]。

現在鋼管混凝土柱剛性節點主要有內隔板節點、外隔板節點、外肋環板節點和隔板貫通節點四種節點形式。隔板貫通節點是在矩形鋼管內設隔板,隔板貫通鋼管壁,鋼管與隔板焊接；鋼梁腹板與柱管壁采用高強螺栓通過連接板連接,鋼梁翼緣與外伸的內隔板焊接[6]。隔板貫通節點雖然須將鋼管柱在節點處斷開,增加了節點區焊縫的長度,但與內隔板節點相比,解決了管柱邊長較小時隔板焊接困難問題和梁翼緣與隔板對中問題,與外隔板節點相比,解決了因隔板太大墻板安裝困難問題,避免了室內角部有凸角現象[7]。但隔板貫通式節點在施工中存在澆筑不方便的問題,隔板孔徑越大,鋼管內混凝土越容易澆灌密實,可是過大的內孔徑會削弱隔板有效受力面積,降低隔板的承載能力[8]。

因此，國內外的學者對方鋼管混凝土貫通隔板節點的隔板孔做了研究。Matsui[9]對方鋼管混凝土柱外隔板節點和隔板貫通節點的設計方法進行了研究,分別提出了兩種節點的容許抗彎承載力計算公式,被日本建筑學會的 AIJ(1987)規程所采納,但兩種方法均忽略了鋼管對節點承載力的貢獻。Shim等[10]以內隔板開口尺寸等為考察的主要參數,進行了鋼管混凝土柱與鋼梁節點的靜力及滯回性能試驗研究,研究表明內隔板圓孔的開口率達到50%,試件的強度幾乎不會降低。苗紀奎等[11]對方鋼管混凝土隔板貫通節點進行研究,研究認為隔板厚度宜大于或等于梁翼緣厚度,建議澆筑孔徑R取值范圍為：a-bf≤R≤bd-bf(其中a為鋼管混凝土柱的邊長；bf為梁翼緣的寬度；bd為隔板的寬度)。

國內外的專家學者主要是針對方鋼管混凝土隔板貫通節點孔研究較多,但對矩形鋼管混凝土柱弱軸方向的隔板孔的研究卻很少。然而矩形鋼管混凝土柱在現在的鋼結構工程中應用普遍,所以對矩形鋼管混凝土弱軸方向隔板孔的研究很有必要。

1 矩形鋼管混凝土柱隔板構造設計

目前規范對于鋼管混凝土柱隔板設置灌漿孔都是采用居中的圓孔形式,四角部設置透氣孔,不論是方管還是矩形管,都是相同開孔形式,且在規程上給出了隔板承載力計算公式,可以方便工程師應用。隨著國家裝配式建筑的推進,鋼結構住宅也得到了發展和應用。對于鋼管混凝土柱,采用矩形鋼管較方管更適合居住建筑,能很好地解決露柱問題；但是伴隨而來的問題是矩形管弱軸方向剛接梁節點構造問題,目前有采用豎板連接的構造方式。該連接構造將翼緣內力通過豎板進行轉換,實現了節點的彎矩傳遞；在住宅結構中若采用外隔板節點,勢必隔板露出需要包覆,影響建筑視覺感官；若采用隔板貫通節點,則傳統的居中圓孔構造方式,使得孔開不大。這勢必影響混凝土灌漿,因此改變了開孔方式,改為矩形孔或長圓孔形式。見圖1。

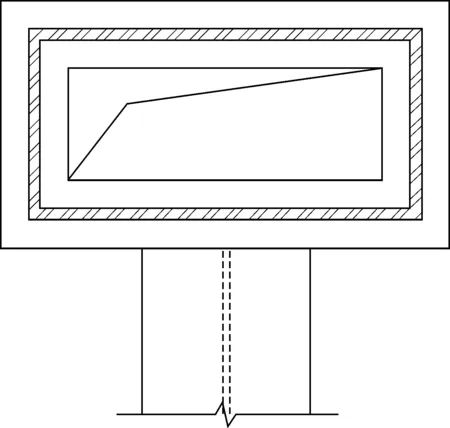
圖1 隔板貫通節點

2 節點受力機理分析

隔板在鋼梁翼緣的拉力作用下,假設為局部均布荷載作用,為約束梁的計算模型。隔板的約束情況比較復雜,兩側面壁板約束較強,可以認為是固端約束,正面壁板對隔板為彈性約束,兩者會共同變形,因此翼緣荷載按兩者的剛度進行分配。隔板的計算模型見圖2,壁板的計算模型見圖3。

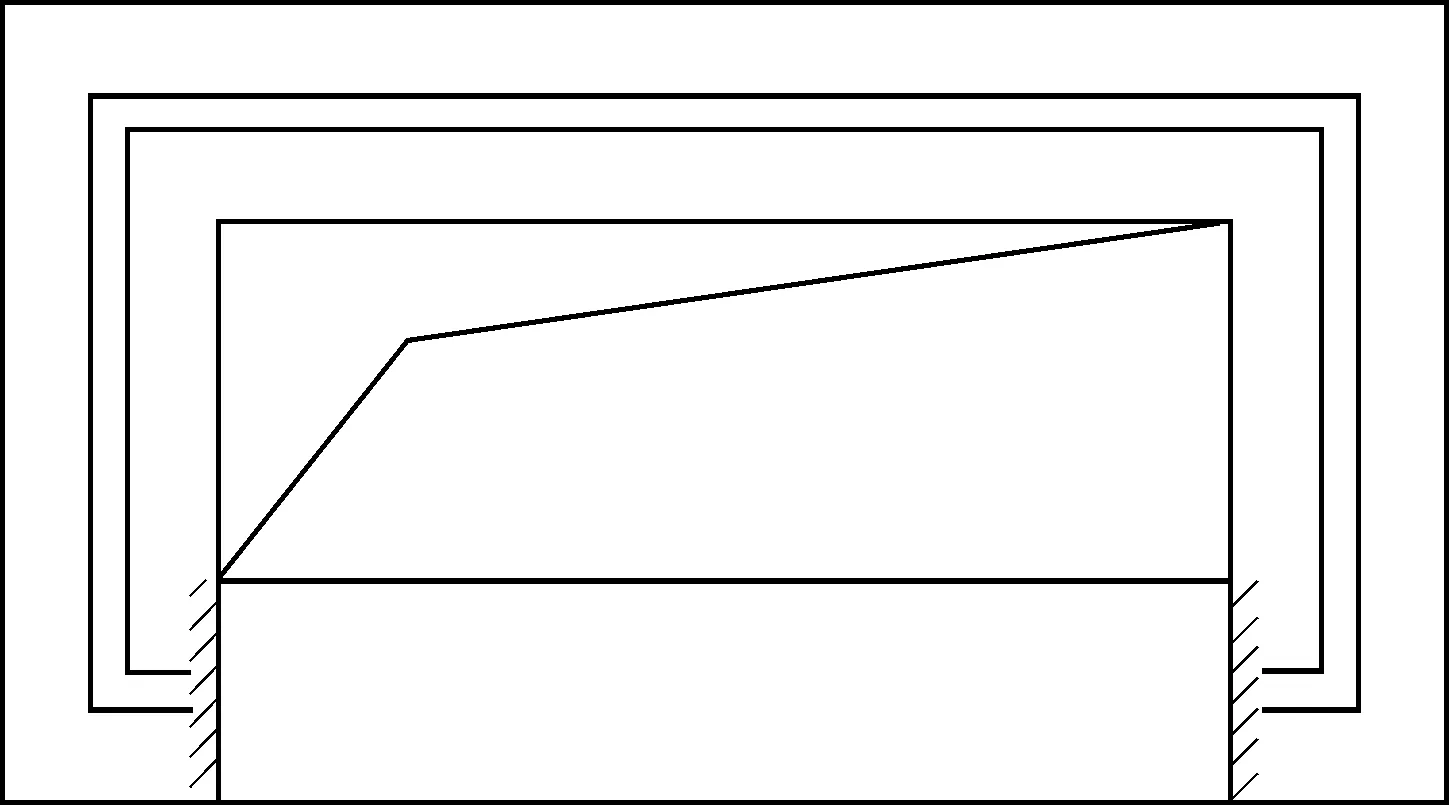
圖2 隔板受力模型

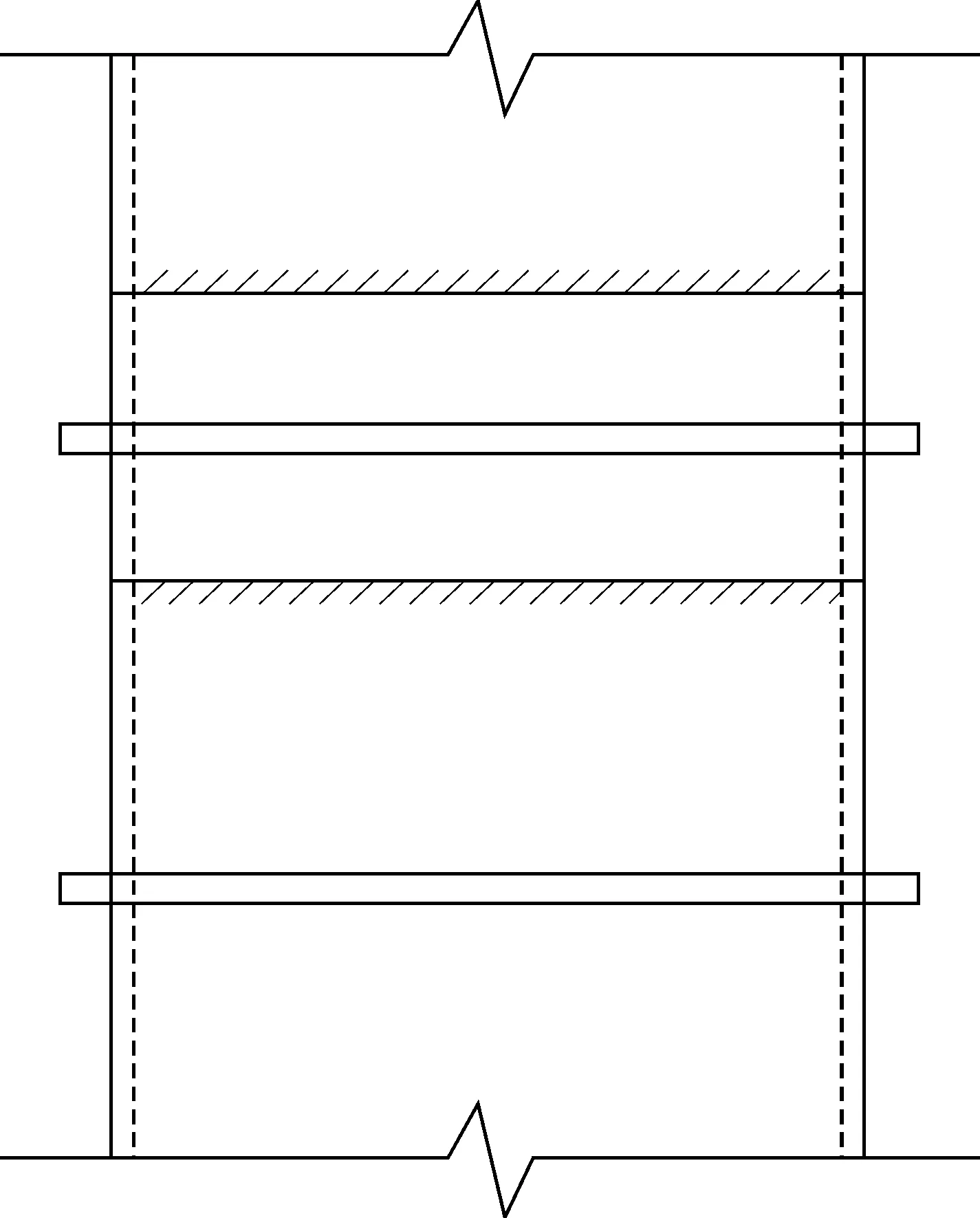
圖3 壁板受力模型

取柱子截面口a×c×t,a為鋼管柱截面長,c為鋼管柱截面寬,t為鋼管柱厚度；隔板厚度為d,外伸寬度為n,則隔板受力模型假定為兩端固端梁,固端梁跨度為l,灌漿孔寬度為f,固端梁截面高度為h=(c+2n-f)/2,固端梁截面寬度即隔板厚度為d。鋼梁翼緣寬度一般小于固端梁跨度,即作用在固端梁跨間局部范圍。假定作用力均布分布在固端梁跨度范圍,則固端梁在單位均布荷載作用下跨中撓度為v1=l4/384EI,則剛度為k1=384EI/l4,其中,I=dh3/12。

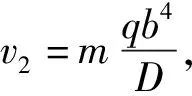
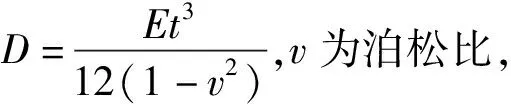
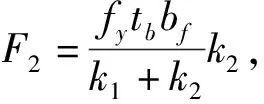
3 算 例

某矩形鋼管混凝土柱的截面高a為350 mm,寬c為170 mm的扁柱,壁厚t為12 mm,弱軸方向連接鋼梁,鋼梁翼緣寬度bf為150 mm,厚度tf為10 mm,隔板厚度d為14 mm,壁板影響高度b為158 mm,鋼材屈服強度fy為345 MPa,灌漿孔長度L為280 mm,灌漿孔寬度f為100 mm。則固端梁高度h=60 mm,固端梁慣性矩I=252 000 mm4,固端梁剛度k1=3 243 N/mm,壁板單位抗彎剛度D=32 597 802 N·mm,a/b=2.215,根據鐵木辛柯《板殼理論》[12]求得m=0.002 64,則壁板剛度k2=3 129.6 N/mm,則壁板上作用的力F2=254 139 N,隔板上作用的力F1=263 360 N,則壁板上作用的線荷載q2=726.1 N/mm,隔板上作用的線荷載q1=940.6 N/mm。

將上述構件采用有限元軟件進行實體建模及數值分析,有限元模型見圖4。經分析得知,當翼緣達到全截面屈服狀態時,隔板剪應力云圖見圖5。鋼梁與隔板的等效應力云圖分別見圖6、圖7。

圖4 有限元模型

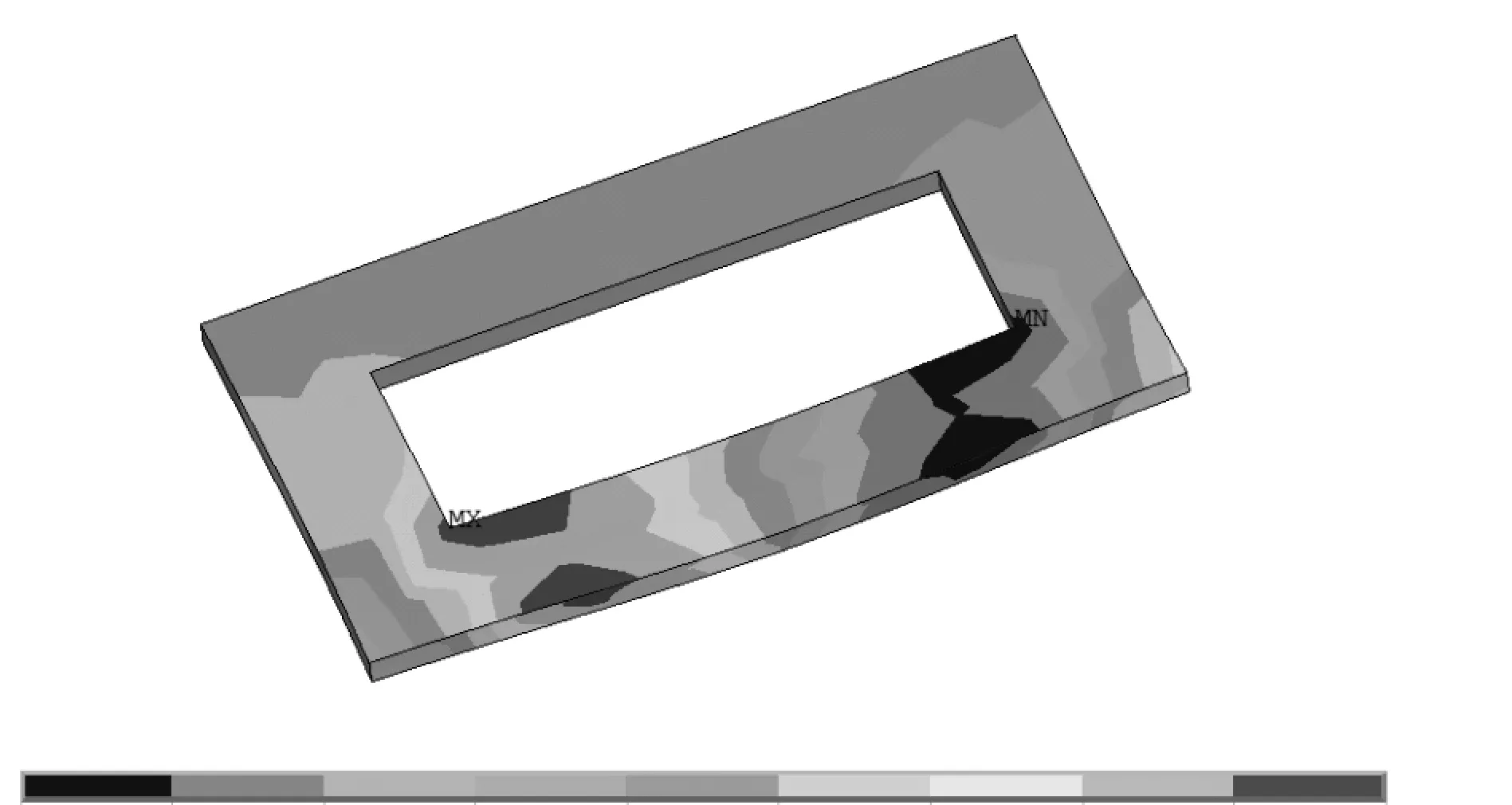
圖5 隔板剪應力

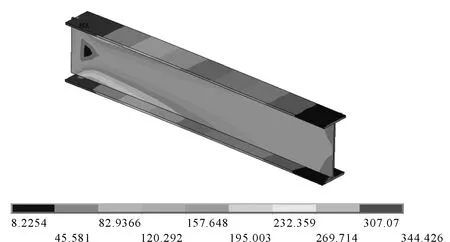
圖6 鋼梁等效應力

圖7 隔板等效應力

從圖5可知有限元模擬得到的剪應力與簡化公式求得的剪應力相當,因此可采用上述公式進行隔板承載力驗算；由圖6與7可知,當鋼梁屈服時,隔板在開孔壁上的受拉區與受壓區進入屈服,也由固端梁的受力模型可以知道位于固端梁的跨中和端部。

4 結 語

對于矩形鋼管混凝土柱,弱軸方向截面高度較小,隔板貫通節點能較好傳遞鋼梁彎矩,但傳統灌漿孔方式孔徑較小,對于混凝土灌漿很不利。改變了傳統的灌漿孔,改為矩形孔,增大了灌漿孔開孔面積,由此帶來的問題是隔板承載力計算沒有現成公式。通過對隔板與壁板的變形協調分析,得出了隔板的受力機理。推導相關公式,并采用有限元數值模擬進行對比驗算,結果是兩者吻合較好。下一步改進灌漿孔,由矩形孔改為長圓孔,是否會改善直角處的應力集中,有待進一步研究。