基于局部結構的渦輪導向器屈曲故障模式分析

張 帆，馮引利，高金海，郭寶亭，蔣文婷

(1.中國科學院工程熱物理研究所輕型動力重點實驗室，北京 100190；2.中國科學院大學，北京 100049)

1 引言

結構屈曲是機械、航空航天、核能等領域普遍發生的故障現象，受到眾多研究人員的重視。早在1961年Timoshenko[1]就對經典屈曲理論進行了較為全面的完善總結。針對各類簡單板殼結構，Gellatly[2]研究了夾層圓筒的屈曲并求出了臨界溫度；Whitney 等[3]運用能量法確定了復合材料層合板的臨界溫度；丁紅麗[4]基于廣義變分原理得出了襯殼彈性屈曲問題的控制方程與邊界條件；Wu等[5]基于Donnell圓筒殼穩定性方程研究了其熱彈性穩定性。對于航空發動機部件等復雜結構，高金海等[6]提出了局部屈曲的理論計算模型并應用于燃燒室屈曲的求解；鄧可順[7]給出了復雜結構屈曲的有限元方程及其解法；吳長波等[8]針對噴管隔熱罩和渦流器的失穩問題做了分析優化；雷友峰等[9]則針對燃燒室蠕變屈曲現場做了理論分析。在試驗研究方面，NASA[10-11]曾在1991 年和2004 年進行過熱機械載荷下航天飛機壁板的屈曲特性試驗；Kicher 等[12]進行了鋼襯圓柱殼的屈曲試驗。

在航空發動機常規靜子件強度校核中，往往重點關注結構靜強度、振動和壽命問題，而忽視薄壁件的熱穩定性問題。國內外學者針對燃燒室機匣的屈曲問題開展過一些研究[6]，但針對渦輪部件在復雜溫度場作用下發生屈曲的問題尚未見報道。

在復雜結構屈曲分析中，往往由于模型過大導致網格劃分不夠精密，輕則影響計算效率，重則得到錯誤的應力峰值，因此復雜結構的屈曲計算及結構優化往往耗費大量時間且優化結果不理想。傳統的屈曲判別與優化方法已難以滿足復雜結構設計需要，亟須提出一種快捷、準確的優化方法。

某型渦扇發動機試車后發現低壓渦輪二級導向器內環發生了波瓣形變形，本文對試驗過程中發生的失效模式進行了分析，提出一種基于子模型的復雜結構屈曲計算方法，可大大簡化計算流程，提高熱結構的分析設計水平。

2 結構應力分析與屈曲計算方法

首先分析結構應力分布，進而提出一種基于子模型的復雜結構屈曲計算方法，通過將整體結構的應力分布等效為子模型的邊界壓應力，計算子模型的屈曲失效。

2.1 導向器結構應力分析

該型渦扇發動機試車后低壓渦輪二級導向器內環發生的波瓣形變形如圖1(a)所示，發動機運行過程中導向器結構的真實邊界如圖1(b)所示。A 點處外機匣與導向器外環直接接觸，并對其產生一定壓力。根據極限條件計算該處壓力為120 MPa。此外，外機匣對A 點導向器外環有周向限位。B 點處外機匣與導向器外環初始設計為間隙配合，但在極限條件下會產生接觸，因此在B 點對導向器外環設置軸向和徑向約束。

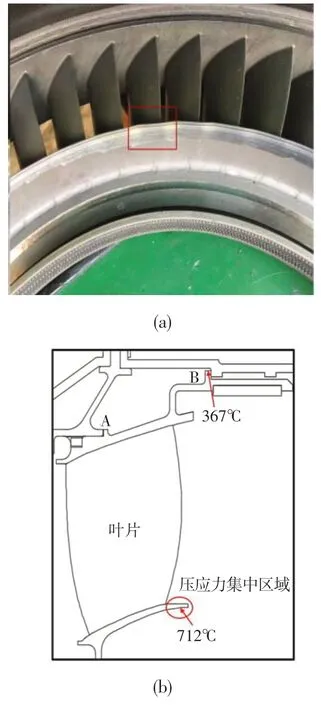
圖1 渦輪導向器波瓣形失效Fig.1 Lobe failure of turbine nozzle

導向器結構除了受外機匣作用力外，還受到因內外涵道氣流溫差引起的沿徑向分布的熱載荷。其中，導向器內環封嚴唇處在極限條件下最大溫度達712℃，整個導向器結構最大溫差達500℃。由于防止氣流倒灌的封嚴唇設計(圖1(b)中紅色圈內)，使得導向器內環封嚴唇處成為懸臂結構，易出現破壞、屈曲等問題。

為校核試驗后出現的變形，首先計算導向器結構在熱載荷和機械載荷作用下的應力分布。導向器結構材料為鑄造高溫合金K403。考慮材料參數受溫度變化影響，材料性能如表1所示。使用Solid185三維8節點固體結構單元對導向器結構進行網格劃分，共得到3 725 972個單元。施加CFD計算得出的溫度場與氣動載荷，計算該邊界條件下的靜應力。最大等效應力與第三主應力的計算結果如圖2所示，可以看出最大等效應力集中在內環輪緣封嚴處，且主要表現為周向壓應力。最大等效應力達屈服強度的2倍，需重點考核該部位的穩定性。

2.2 子模型屈曲計算方法

對于同時受到熱載荷和機械載荷的局部結構，可將其等效為圖3 所示的四邊受壓應力作用，面內受熱載荷，邊長為a、b，厚度為h的固支板。根據該板的控制方程和邊界條件，可推導該子模型的臨界溫度和臨界壓應力。

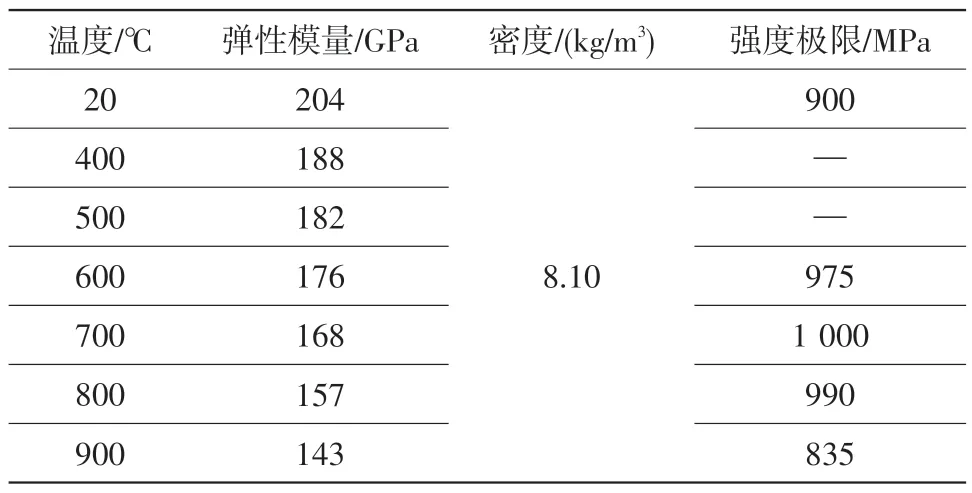
表1 K403的材料屬性Table 1 Material properties of K403

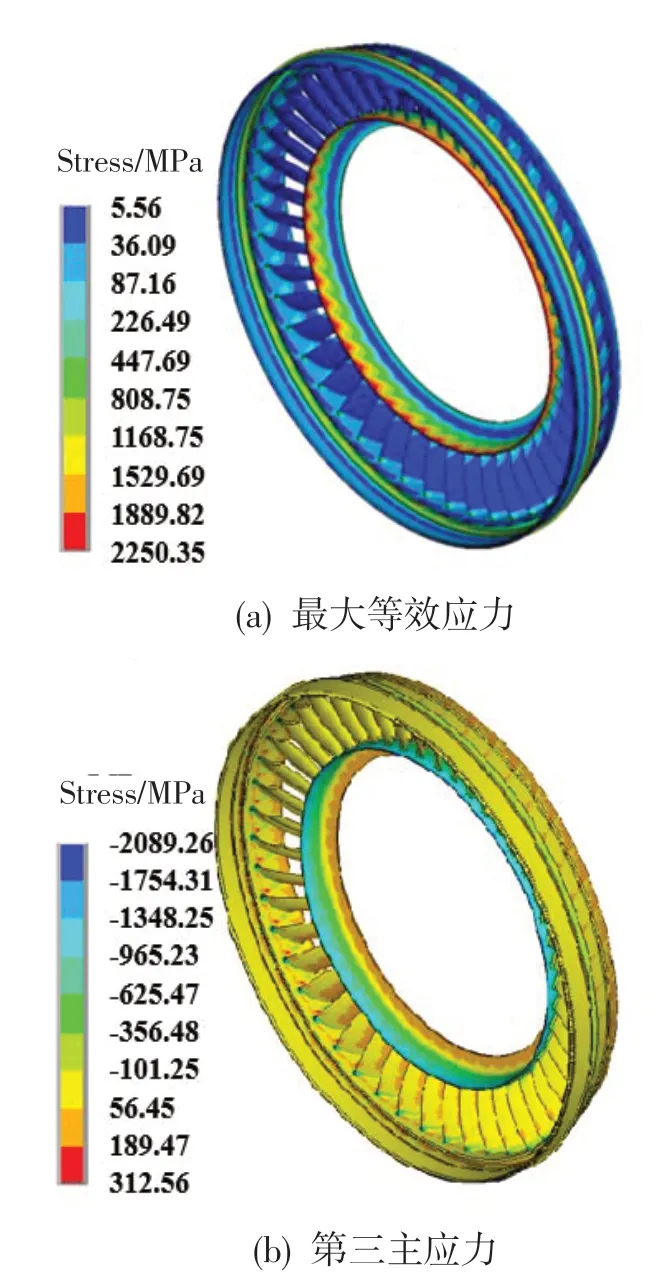
圖2 導向器結構應力分布Fig.2 Stress distribution of turbine nozzle

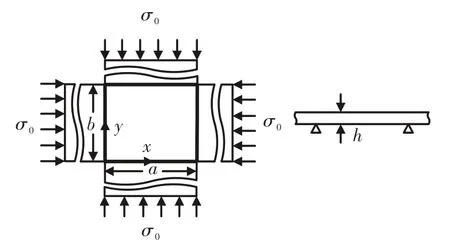
圖3 考慮熱載荷與機械載荷的固支板Fig.3 Fixed plate considering thermal load and mechanical load

固支板四邊撓度均為0，則殼體薄膜內力可以表示為：

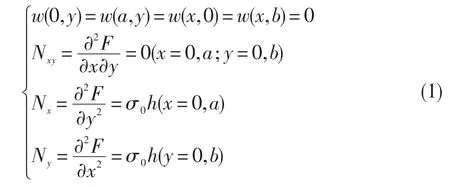
受熱板的無量綱控制方程為：

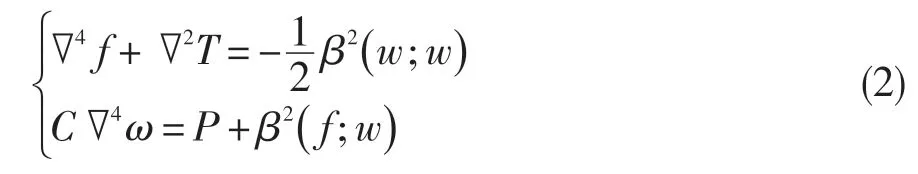
式中：f為應力函數，T為溫度函數，w為位移函數，P表示機械載荷(主要表現為壓力)，β為固支板長寬比，(;)=。

對于承受熱載荷和機械載荷(主要為壓應力，由其他非熱載荷引起)的固支板，采用初始后屈曲漸進分析理論對非線性控制方程進行求解，可得到含有熱載荷項和機械(或氣動)載荷項的特征值方程式[13]，進而得到局部結構的臨界壓應力為：

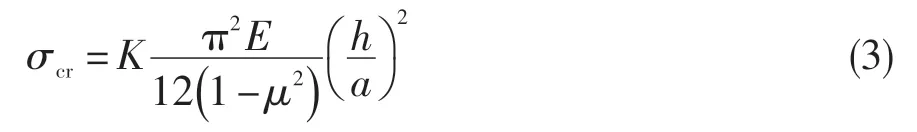
式中：K為β的函數。

根據前文應力分析結果，導向器內環封嚴唇存在壓應力集中，可將其近似為薄壁圓筒，如圖4 所示。由于該局部結構僅一側截面存在外部等效邊界條件，故可以提取左側與整體結構連接處的位移邊界條件和圓筒壁面的壓應力。若將其近似等效為懸臂圓筒，即左側撓度為零，則其屈曲臨界壓力可表示為：

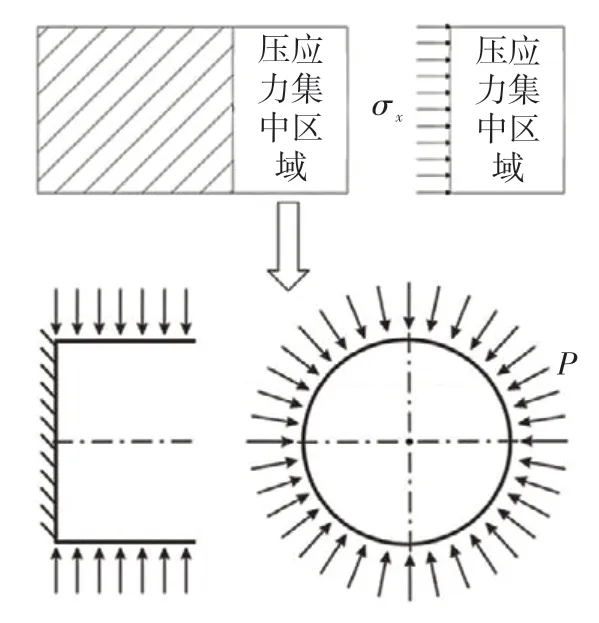
圖4 導向器局部結構示意圖Fig.4 Local structure diagram of turbine nozzle

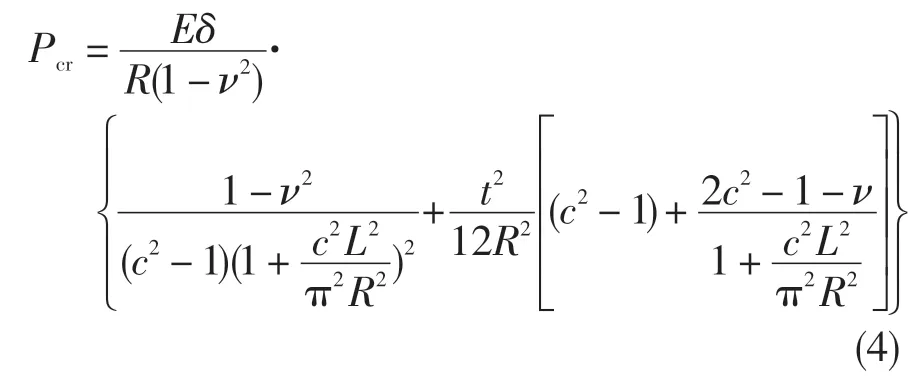
式中：δ為圓筒厚度，R為圓筒半徑，L為圓筒長度，c為圓筒屈曲波數。

由懸臂圓筒受壓屈曲理論公式可以看出，除邊界條件外，影響圓筒屈曲的重要因素包括圓筒的半徑、厚度和長度。

3 局部屈曲求解與結構優化

3.1 屈曲有限元計算方法

子模型計算屈曲的重點在于如何準確提取局部結構的邊界條件，而借助有限元軟件可簡易、快速提取。機械載荷與熱載荷同時作用下的節點力可表示為：

同時，幾何剛度矩陣由兩部分構成：

式中：[Kg,P]、[Kg,T]分別為與載荷和溫度場有關的剛度矩陣。

據此可將穩定性方程寫為：

現有大型有限元計算軟件可以實現局部結構邊界條件提取，從而對局部結構進行特征值屈曲計算。首先計算全尺寸模型下的應力分布結果，提取壓應力最大處的局部結構，并將局部結構外部應力或邊界的影響作為邊界條件提取，最后計算局部結構的特征值屈曲。在有限元軟件中提取局部結構求解的具體步驟如圖5所示。

提取導向器的內環封嚴唇結構，然后分別對提取結構和整體結構進行特征值屈曲求解，得到的屈曲波形如圖6 所示，屈曲安全系數為1.25。屈曲波形與試驗結果完全一致，均體現為內環輪緣封嚴處的波瓣形屈曲，證明該結構確實存在極大屈曲風險。

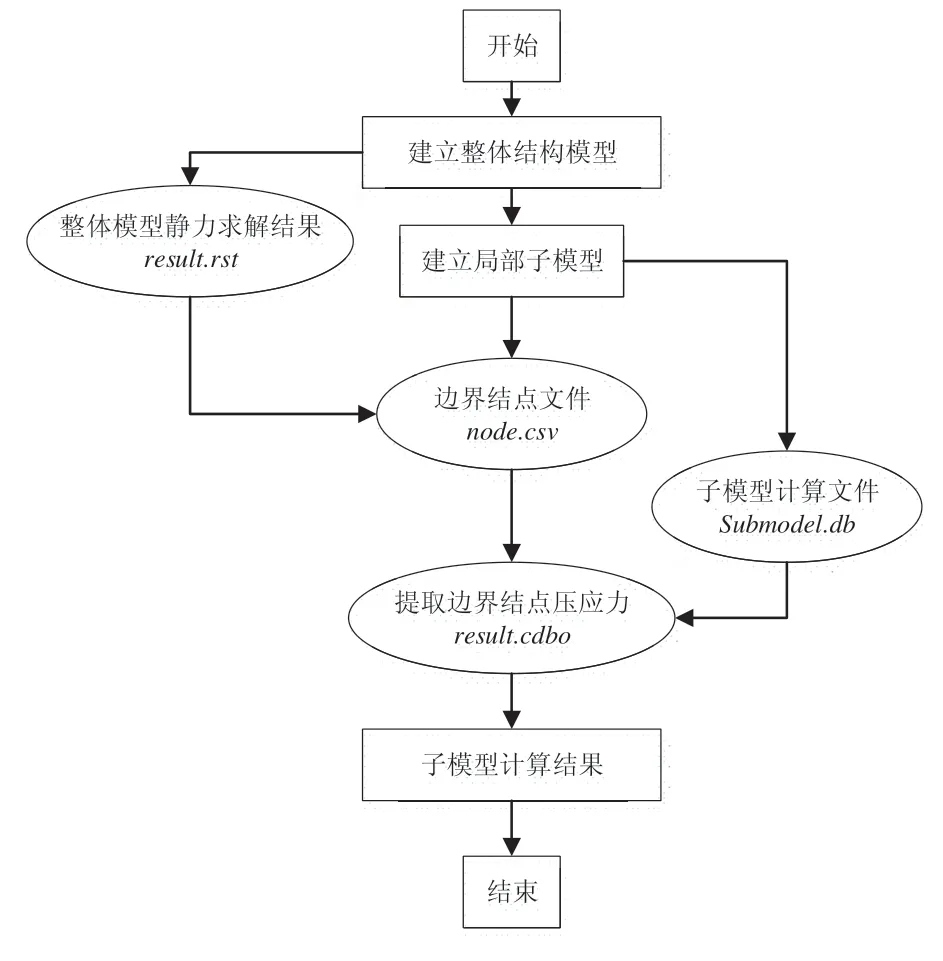
圖5 局部結構在有限元程序中的計算步驟Fig.5 Calculation steps of local structure in finite element program

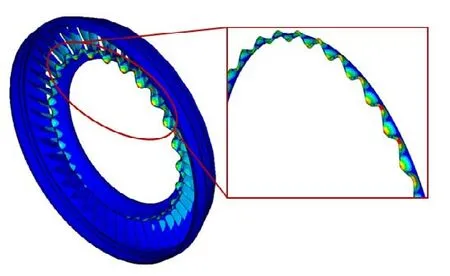
圖6 局部屈曲計算Fig.6 Local buckling calculation

受壓情況下構件的彈性屈曲被認為已經破壞，屈曲安全系數是判斷結構件穩定性是否滿足條件的重要參數，其表達式為：

式中：Pk為臨界載荷，Pmax為飛行包線內機匣可能發生的最大工作載荷。

根據航空發動機結構設計準則[14]，對于民用發動機，要求發動機機匣的屈曲安全系數大于2.0。

綜上看出，防屈曲設計可從改變載荷環境、改變邊界條件和優化結構幾何外形三個方面實現。若在不改變該結構的條件下對溫度場進行優化，可以通過空氣系統的設計降低整體結構的溫度梯度，但此類做法需對發動機結構進行較大變動。優化導向器結構幾何尺寸和在質量允許范圍內強化結構則成為優化方向。

3.2 導向器局部結構的優化

結合薄壁圓筒的理論解和有限元計算公式，可將局部結構屈曲安全系數描述為：

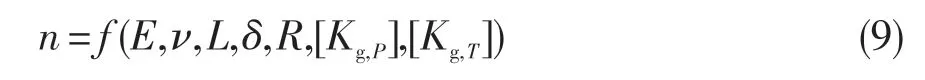
式中：E、ν分別為材料的彈性模量和泊松比。

在不改變載荷和邊界條件的情況下，要提高薄壁圓筒件的穩定性，只能通過增加圓筒壁厚度的方法。對比兩種增加厚度的方法，即封嚴唇整體加厚或部分加厚(圖7方案1與方案2)。極限狀態下整體加厚后的屈曲安全系數見表2，可見整體加厚之后屈曲安全系數可以滿足設計準則要求。但屈曲波形沒有發生變化，且系數裕度較低，仍存在一定屈曲風險。

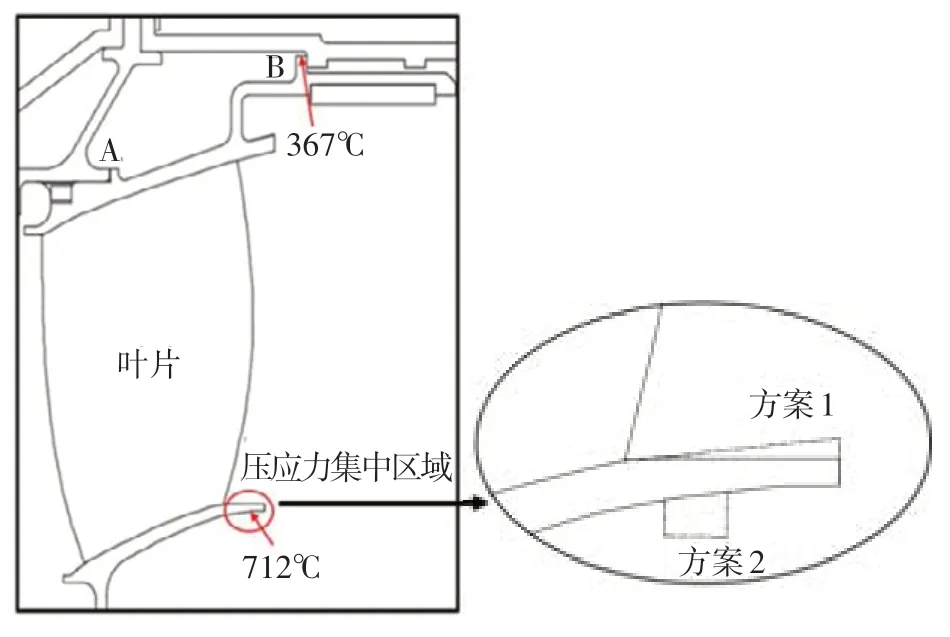
圖7 局部加厚與整體加厚方法Fig.7 The method of local thickening and integral thickening

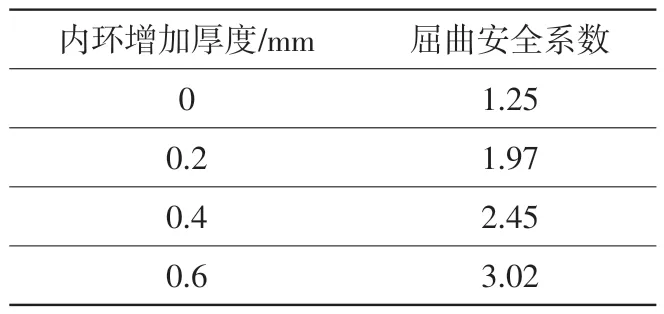
表2 整體加厚后的屈曲安全系數Table 2 Buckling safety factor after integral thickening

若考慮局部加厚，即在內環內壁面添加環形加強肋，熱應力大幅下降，屈曲安全系數增加到12.21，且屈曲波形發生改變，一階屈曲波形表現為節徑型，很好地解決了此類失效問題。故最終選擇在內環內表面添加環形加強肋。

3.3 針對邊界條件的優化

根據極限狀態點應力計算結果，A 點徑向壓力與B 點約束邊界條件均對熱應力產生了較大影響，下面通過有限元計算研究此兩個邊界變化量對屈曲安全系數的影響。為此，設置如表3所示的7個不同邊界條件計算組。其中，1～4組計算研究A點處外機匣對導向器產生的徑向壓力對結構屈曲的影響，4～7組計算研究B點處導向器外環因熱膨脹造成的徑向位移對結構屈曲的影響。

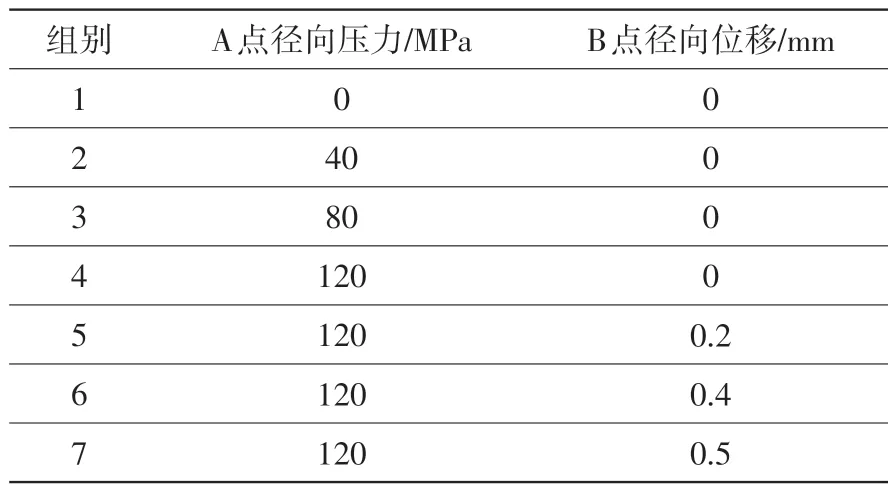
表3 邊界條件計算組Table 3 Boundary condition calculation group

首先考慮A 點壓力約束對屈曲安全系數的影響。根據1～4 組條件計算的屈曲安全系數隨A 點徑向壓力的變化關系如圖8(a)所示，可見隨著徑向壓力的減小屈曲安全系數大幅增加，因此A 點邊界可以作為優化目標。其次考慮B點位移約束對屈曲安全系數的影響。根據4～7 組條件計算的屈曲安全系數隨B 點徑向位移的變化關系如圖8(b)所示，可見屈曲安全系數隨著徑向位移的增加而增大，但其增度低于A 點壓力減小時的增度。據此，僅選擇A點作為優化對象。將與A點接觸的外機匣改為齒形結構，如圖9所示。

根據本節分析結果可以看出，除在導向器內環內壁面增加加強筋外，改變與A點接觸外機匣結構，將外環與外機匣連接處改為齒形結構，使其不對A點產生徑向壓力，可以很好地解決此種屈曲失效問題。在后續的發動機試車中未再出現此故障，驗證了優化方向的正確性。

4 結論

針對航空發動機試車后發現的導向器屈曲現象開展了相關研究，主要得到下列結論：

(1)試車后出現的導向器內環波瓣形失效，為熱載荷與機械載荷聯合作用的熱屈曲問題。

(2)除邊界條件外，影響懸臂圓筒屈曲的重要因素還包括圓筒的半徑、厚度和長度。

(3)借助有限元軟件可簡易快速地提取局部結構的邊界條件，以屈曲安全系數為優化目標得到的導向器內環壁面增加加強筋和改變A點接觸外機匣邊界的優化結構，均可以很好地解決屈曲失效問題。

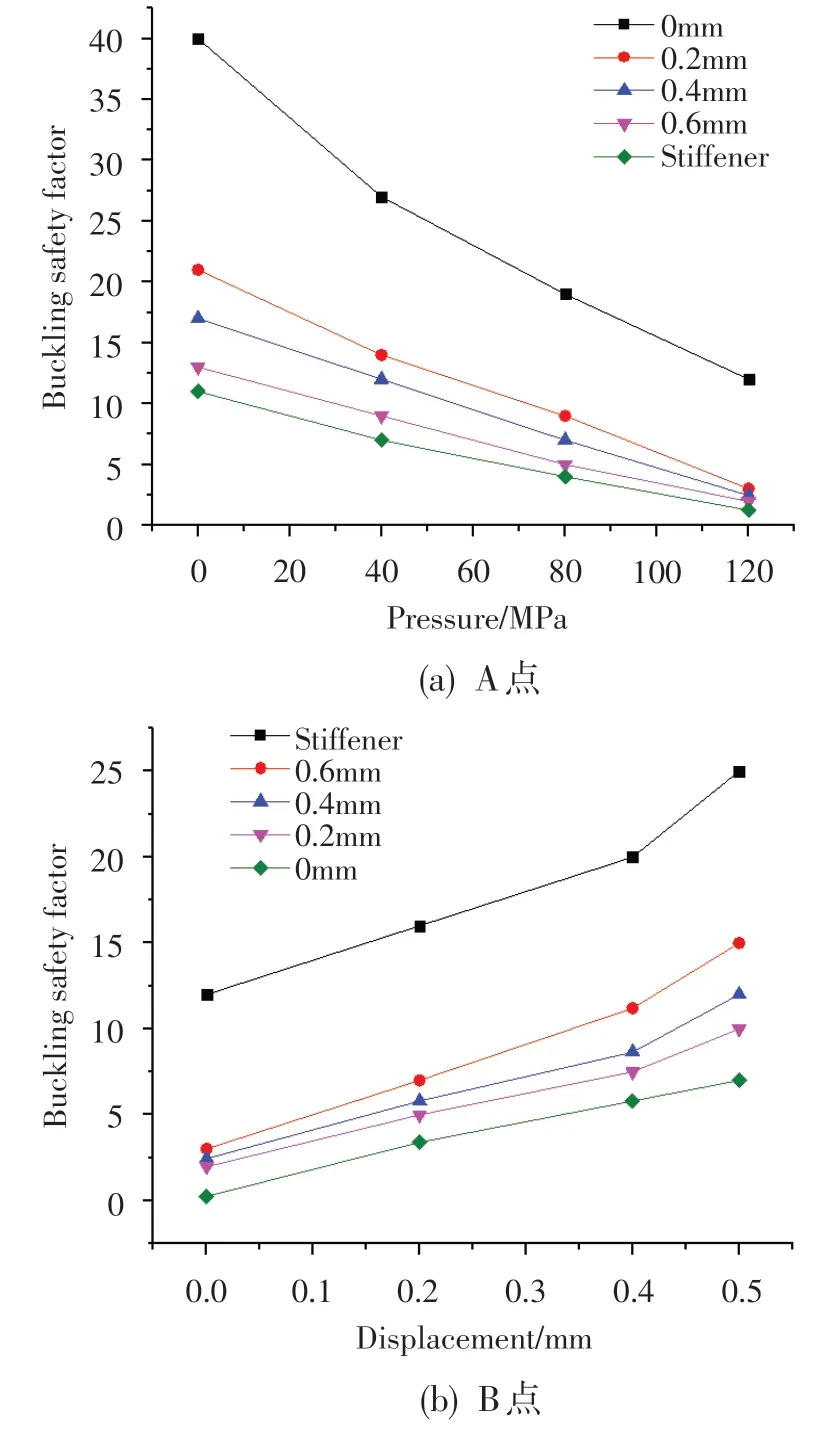
圖8 屈曲安全系數隨A點徑向壓力和原有B點徑向位移的變化關系Fig.8 Variation of buckling safety factor with radial pressure of A point and radial displacement of B point

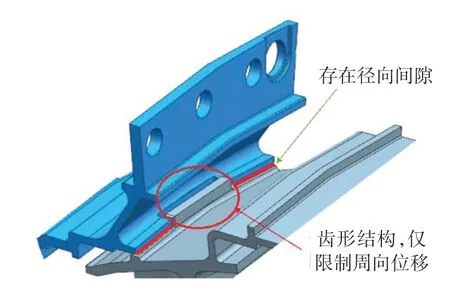
圖9 導向器齒形結構Fig.9 Tooth structure of turbine nozzle