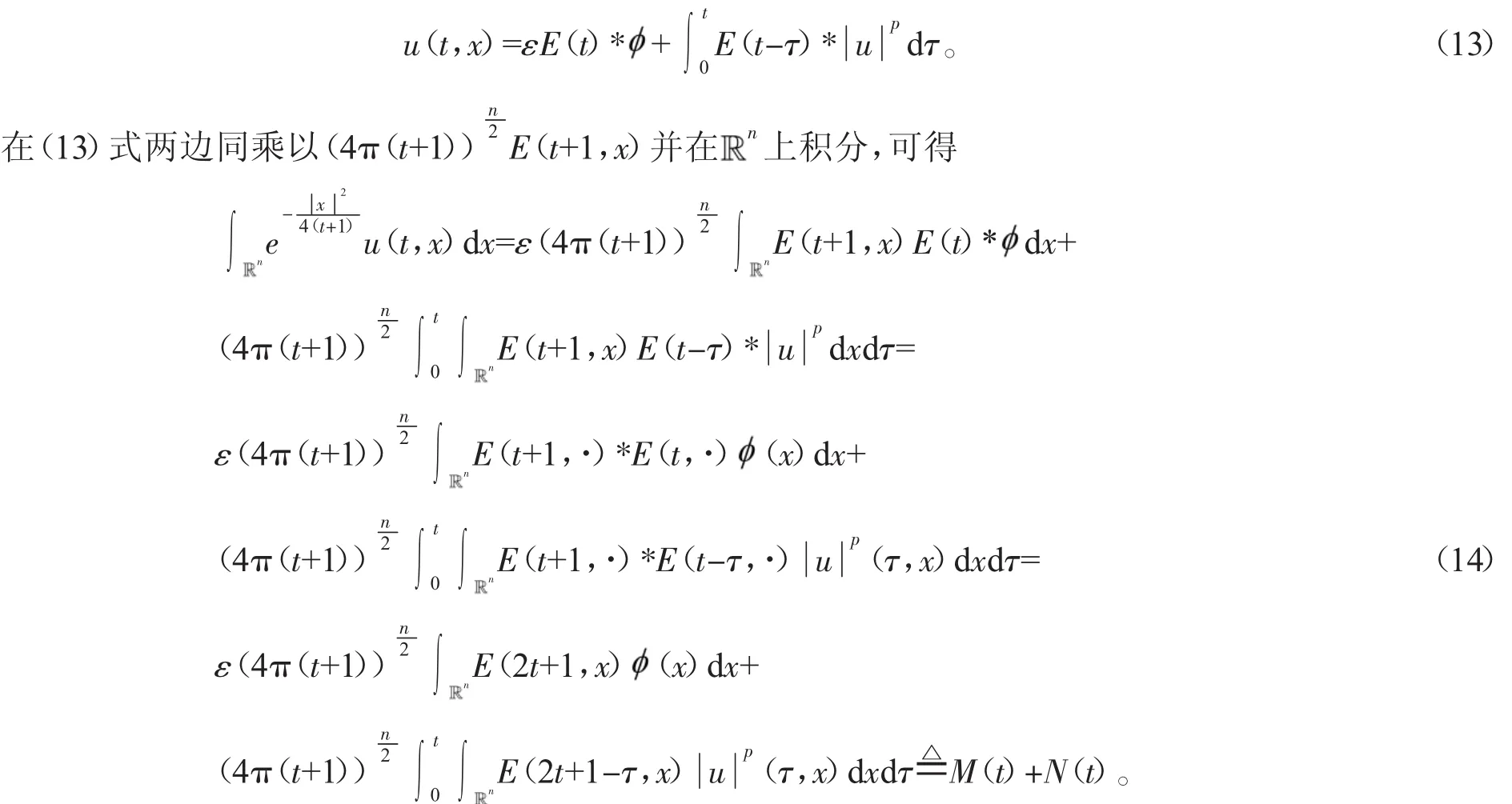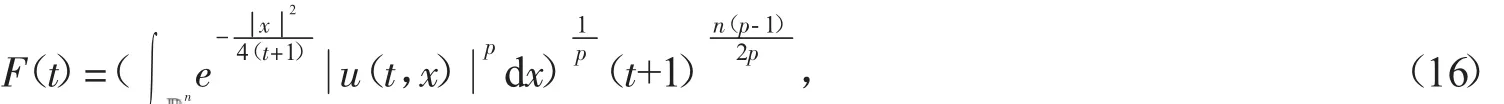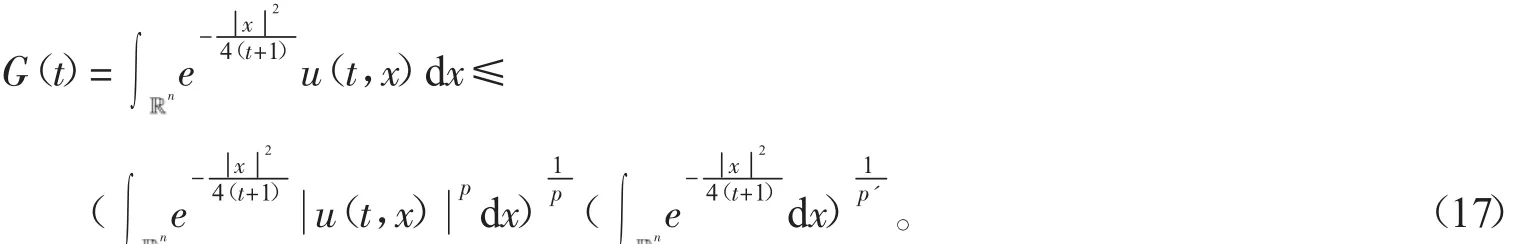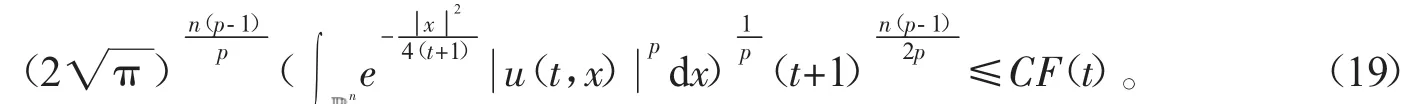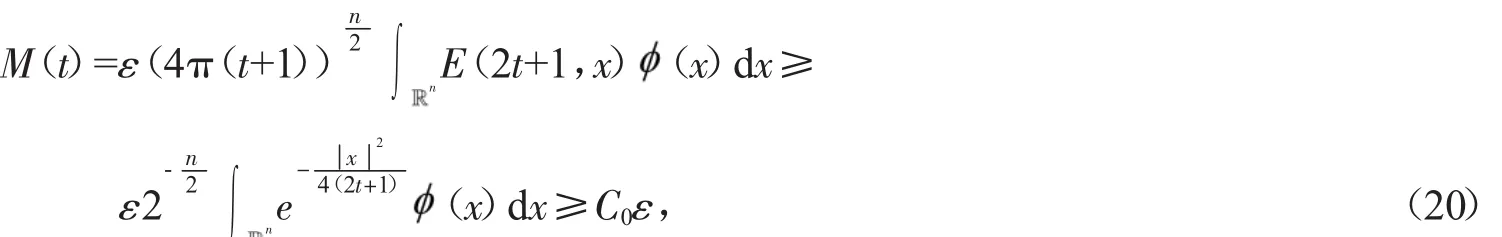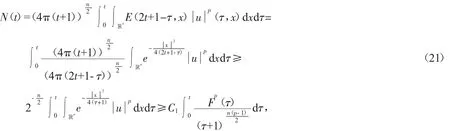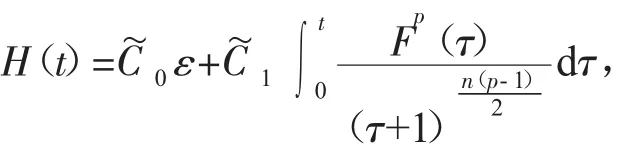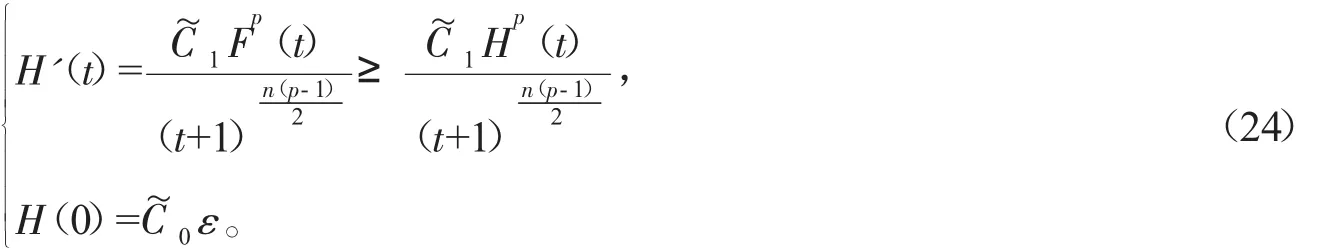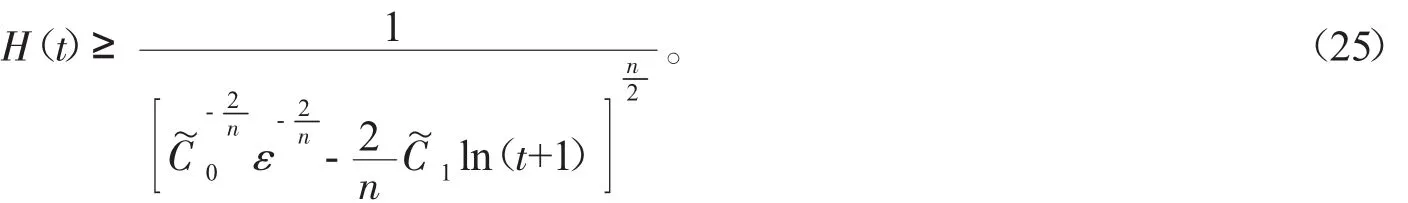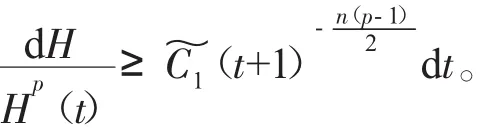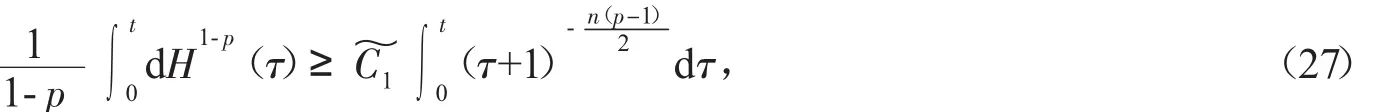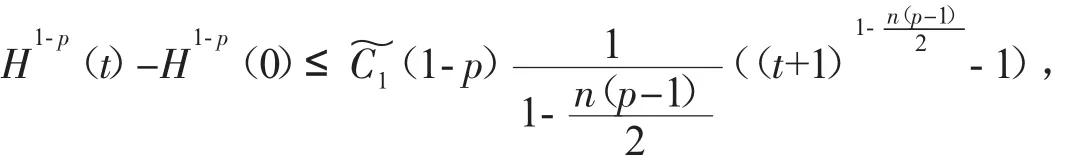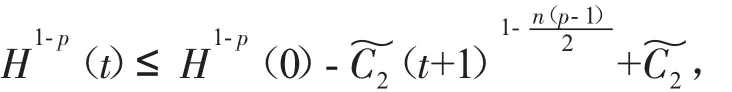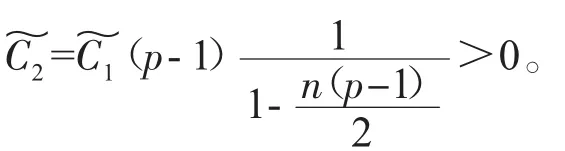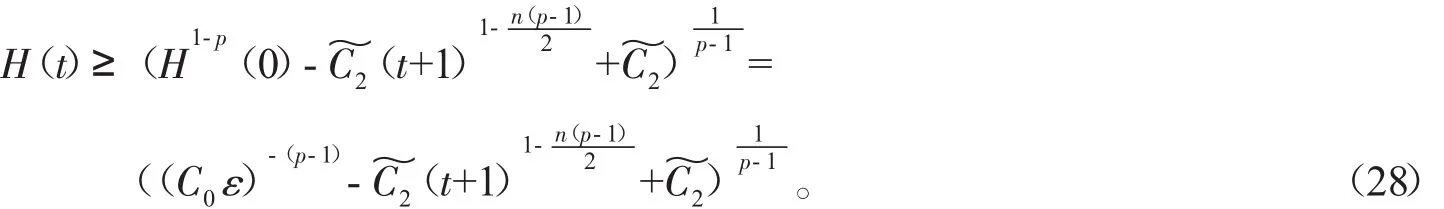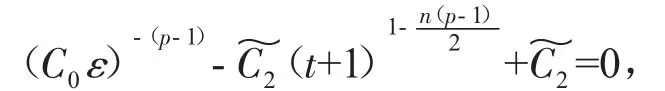半線性熱傳導方程Cauchy問題生命跨度估計
林銀河,徐根海,楊姍姍
(1.麗水學院工學院,浙江麗水323000;2.浙江理工大學理學院,浙江杭州310018)
0 引言
根據定義,生命跨度T(ε)是指解的最大存在時間。當T(ε)=+∞時,表明解整體存在。Li和Chen[1]建立了如下形式的生命跨度下界估計:
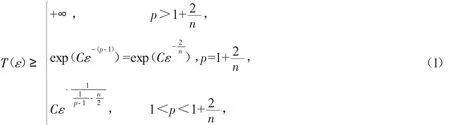
其中C是一個與n,p有關的正常數,但與ε無關,不同的地方取值不一樣。
現在研究以下n維半線性熱傳導方程的Cauehy問題:

和

其中ε表示描述初值小性的參數。上述兩個問題的方程都是反映擴散的方程,通常用于種群動力學和幾何學中。這兩個問題的主要區別在于非線性項,問題(2)中的非線性具有非負性,這有利于得出下界估計,而問題(3)的非線性不具有非負性。與上述兩問題相關的更一般的非線性熱傳導方程模型為

其中u(t,x)表示化學反應中的溫度,(f正)表示熱源,可參考Hu[2]關于模型(2)的詳細介紹。對Cauchy問題(2)的研究源于Fujita[3]于1966年的開創性工作。他證明了問題(2)存在臨界指標p=pF(n)=(Fujita臨界指標):即當時,對于任何非負且非平凡的初值,解將在有限的時間內破裂:而當p時,則存在小初值整體解。隨后,文[4-7]研究了臨界指標情況,并證明了該情形解也將在有限時間內破裂。另外,Hu在文[2]的第5章中用反證法證明了當1 有一個有趣的現象是以下小初值半線性耗散波動方程的柯西問題: 與(2)具有相同的臨界指標,參見[8-14]及其中的參考文獻。 引理1 熱核E(t,x)的傅里葉變換為 證明 由傅里葉變換的定義可知 于是(8)得證。基于此,可以證明 E(t,x)的半群性質,即: 其中★表示卷積。 證明 由(8)式可知E(t,x)的傅里葉變換為 由此可得 對上式再作傅里葉逆變換便可得(10)式。 首先考慮定理1的證明。根據Diuhamel原理,問題(2)的解可以表示為 在這里我們使用了E(t,x)的半群性質。 令 和 則由 Ho¨lder不等式,可得 令 則有 代入(17)式,得 其中C0表示一個與ε無關的正常數。 注意到當 0≤τ≤t時,有 2(t+1)≥2t+1-τ≥t+1,則由 Ho¨lder不等式可以估計非線性項 N(t): 其中C1表示一個與ε無關的正常數。 結合(13)(19)(20)和(21),可得 令 則有 和 由此可得H(t),亦即F(t)的生命跨度上界估計: 積分上式,可得 即 整理后,可得 其中 進一步,可得 于是當 即當 時,有 從而 這樣就證明了生命跨度上界估計為 從而完成了定理1的證明。 以下考慮定理2的證明。事實上,只需要證明解的非負性,則問題(3)就能轉化為問題(2),從而就可以用上面的方法得到同樣的生命跨度上界估計。下面證明問題(3)的解是非負的。首先考慮如下Cauchy問題: 由熱傳導方程基本解的正性(見(13))和初值的假設,可知 再由熱傳導方程解的唯一性,可知 這樣就證明了Cauchy問題(3)解的非負性,從而問題(3)中的非線性項,故只需重復定理1的證明步驟即可證明定理2。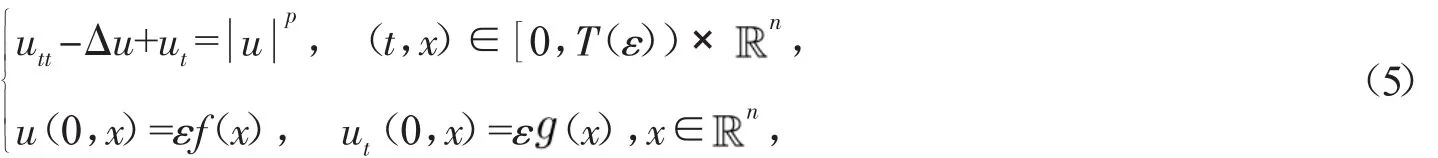
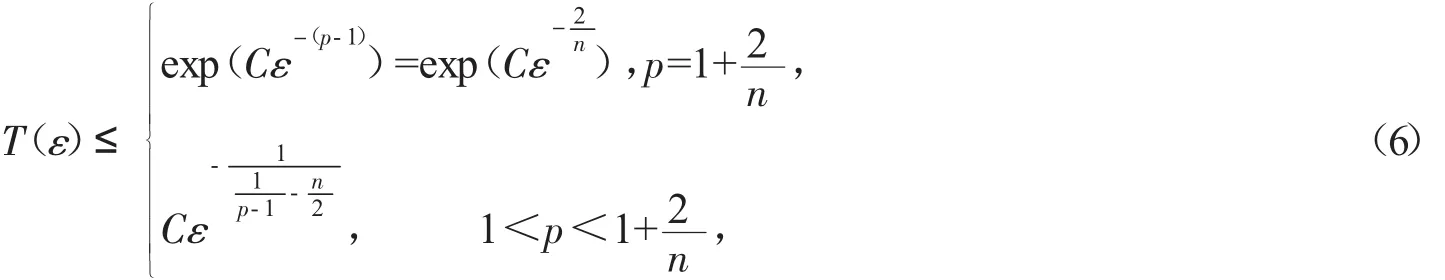
1 熱核的半群性質






2 主要結論的證明