位移載荷下折疊式壓電振子的疲勞分析

趙春明，龔立嬌，周天爍，張 新，張鵬飛

(石河子大學 機械電氣工程學院，新疆 石河子 832003)

0 引言

壓電俘能器利用壓電材料的正壓電效應將振動能轉換為電能，通過匹配能量采集電路，為負載提供電能。通常壓電俘能器的結構簡單且易發電，因而國內外專家已廣泛研究[1-2]。本文提出的一種折疊式壓電振子結構[3]由壓電層、彈性層和粘結層組成。在實際應用中，壓電振子的固有頻率與環境的振動頻率接近，使其機電轉換性能得到充分利用。相應地，隨著交變位移作用，折疊壓電振子的各部分材料將會出現疲勞現象，直至結構產生破壞。由此可見，疲勞壽命將成為影響壓電振子輸出電能的一個重要因素[4-5]。

目前對壓電振子振動發電性能的研究較多，而其中粘結層對壓電結構性能的影響顯著[6-7]。Jurk M等[8]給出了評估粘結層對壓電式傳感器質量影響的方法。Jin Congrui等[9]提出了粘結層的幾何與材料特性對單晶壓電振動懸臂梁結構的機電耦合的影響。Anil Can Turkmen等[10]設計了一種拔型壓電能量采集裝置，將其嵌入人的鞋跟中，通過人行走時自身體重作為諧波載荷作用在裝置上。當質量為90 kg的人正常行走時，可產生的電能為1.43 mW，但未考慮裝置的使用壽命。張淼等[11]通過給懸臂梁式壓電振子施加位移激勵，然后對壓電層進行疲勞分析，但未考慮粘結層對壓電振子的疲勞影響。在實際應用中，壓電振子由于各層間邊緣處的不連續及材料參數差異較大，而粘結層表面會出現復雜的應力分布，且在中間層的兩端圓角位置會出現高度的應力集中，這影響了壓電結構的使用壽命。

本文針對一種折疊式壓電振子，對其粘結層進行理論分析，通過Ansys Workbench建立有限元模型；同時考慮在位移載荷下，分析粘結層厚度對折疊式壓電振子的彈性層和壓電層的應力影響；將靜力分析結果傳輸到nCode DesignLife疲勞軟件，對壓電層進行疲勞壽命分析。

1 折疊式壓電振子粘結層理論分析

折疊式壓電振子由彈性折疊梁、壓電片及粘結層組成，如圖1(a)所示。彈性折疊梁的上、下表面粘貼壓電陶瓷片，折疊梁的長、寬、高分別為L、W、H，彈性層的厚度為h2；壓電片的長度、厚度分別為lp,h1(h3)；粘結層的厚度為ha。建立折疊式壓電振子的局部坐標系如圖1(b)所示。圖中，x1(x3),x2分別為壓電層、彈性層的橫坐標，z1(z3),z2分別為壓電層、彈性層的縱坐標，u1(u3),u2分別為壓電層、彈性層的軸向位移，w1(w3),w2分別為壓電層、彈性層的橫向位移。

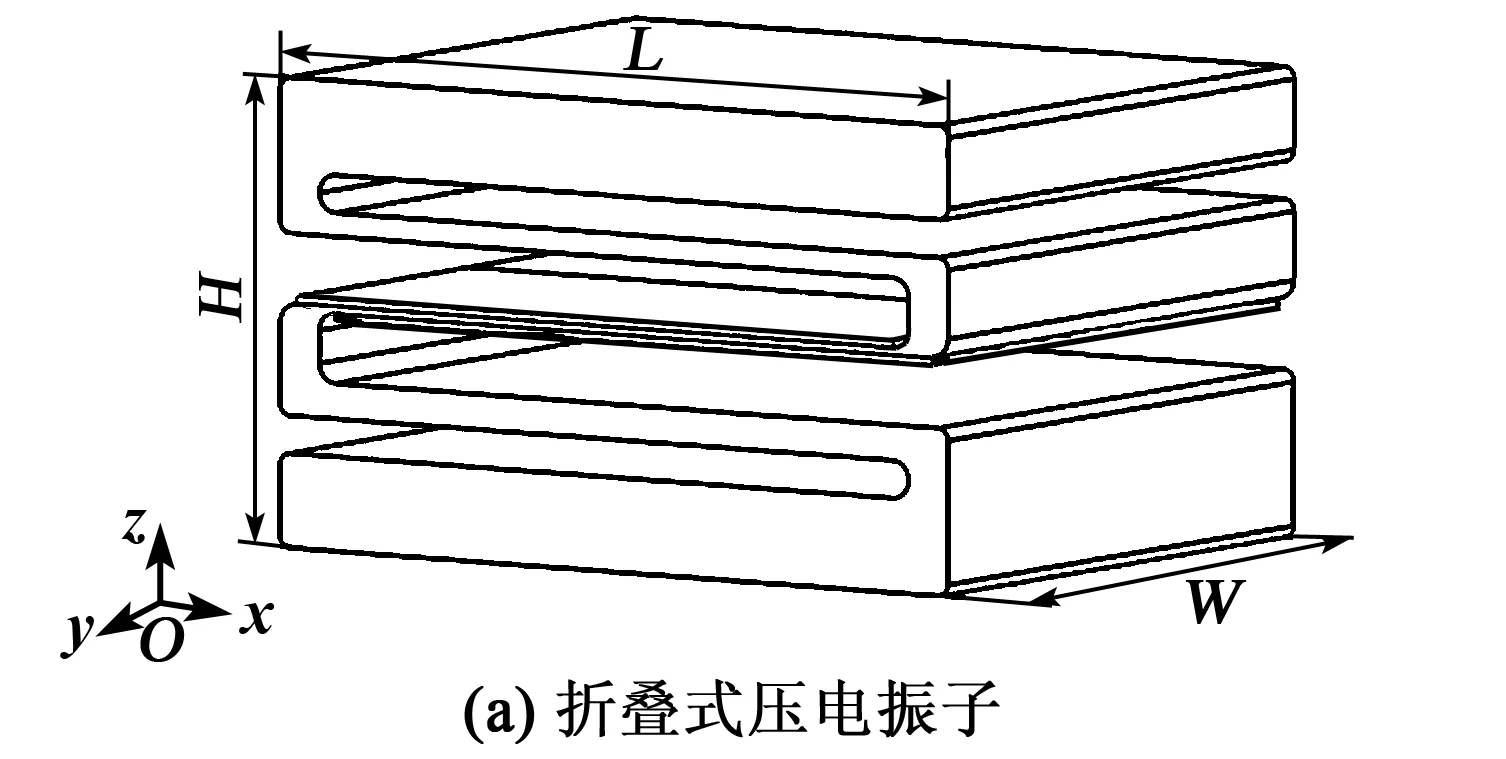
圖1 折疊式壓電振子結構

假設折疊式壓電振子中層與層的材料參數與幾何參數不同，而同一層的材料性能與厚度相同，各層材料為各向同性材料，則折疊梁各層中任一點的軸向位移Ui(xi,zi,t)及橫向位移Wi(xi,zi,t)[12]分別為

(1)

Wi(xi,zi,t)=wi(x,t)

(2)

粘結層1、2的上、下表面軸向位移U′1、U″1、U′2、U″2分別為

(3)

(4)

(5)

(6)

粘結層1、2的剪應變分別為

(7)

(8)

折疊梁的微元體受力分析如圖1(c)所示。各層中存在軸力Ni、彎矩Mi和剪力Qi(i=1(3)，2表示壓電層和彈性層)；τ1(2)，σ1(2)分別為粘結層1、2的切應力和剝離應力。

為便于分析計算，粘結層內的剪切應力、剝離應力沿其厚度方向保持不變，同時可忽略粘結層慣性力的影響。粘結層1的切應力：

(9)

剝離應力：

(10)

粘結層2的切應力：

(11)

剝離應力：

(12)

式中Ga,Ya分別為粘結層的剪切模量和彈性模量。

隨著位移載荷作用在折疊壓電振子上，中間層產生彎曲變形。為了防止折疊式壓電振子在粘結層處剪切破壞，根據式(1)、(2)可推導出粘結層的剪應變、切應力及剝離應力。由式(7)、(9)、(10)可見，對于折疊式壓電振子，隨著粘結層厚度的減小，其剪切強度增大；而粘結層的切應力、剝離應力增大，則會產生折疊壓電振子的疲勞破壞，減少使用壽命。因此，本文通過施加位移載荷，研究了粘結層厚度對折疊式壓電振子的疲勞壽命影響。

2 折疊式壓電振子的建模與靜力分析

2.1 建模方法與過程

由圖1所示的一種折疊式壓電振子，本文選用Ansys Workbench軟件建立有限元模型。在建模過程中，粘貼于中間薄梁上、下表面的4個壓電陶瓷片，因同一層的變形區域相同，可等效粘貼為上、下兩個壓電片。

折疊梁結構尺寸：L=34 mm，W=27 mm，H=19.5 mm，h2=0.3 mm，lp=32 mm，h1=h3=0.22 mm。粘結層長為32 mm，ha=0.01～0.1 mm。構成折疊式壓電振子的材料：彈性折疊梁選用304鋼，壓電材料選用P-51，粘結層選用膠體材料環氧樹脂膠，具體參數如表1所示。

表1 折疊式壓電振子參數

設置折疊式壓電振子的材料屬性，然后進行網格劃分。彈性折疊梁與粘結層可采用四面體單元類型，壓電層采用六面體單元類型。而在中間薄梁兩端圓角的過渡位置，為避免應力奇異點，可采用局部網格優化。圖2為折疊式壓電振子的有限元模型。

圖2 折疊式壓電振子有限元模型

2.2 折疊壓電振子靜力分析

網格劃分后，對折疊式壓電振子進行靜力分析。假設粘結層在彈性層與壓電層之間均勻分布，位移連續，且彈性層與壓電層受力均勻。通常，粘結膠體材料的剪切強度數值越大，其粘接的強度越高。本文粘結層的性能參數取室溫(25 ℃)，粘結強度(即拉伸極限強度)為31 MPa。

對折疊式壓電振子的底面采取固定約束，其彈性層、壓電層的應力分布對應以下3種工作模式：

1) 頻率為85.5 Hz時，在折疊壓電振子的最上層質量塊的左側面施加大小1 mm、方向豎直向下的位移載荷，分析得到等效應力分布云圖，如圖3(a)所示。

2) 頻率為105.8 Hz時，對折疊壓電振子的上表面施加大小為1 mm、方向豎直向下的位移載荷，分析得到等效應力分布云圖，如圖3(b)所示。

3) 頻率為153.2 Hz時，對折疊壓電振子最上層質量塊的前、后面均施加大小為1 mm、方向豎直向下的位移載荷，分析得到等效應力分布云圖，如圖3(c)所示。

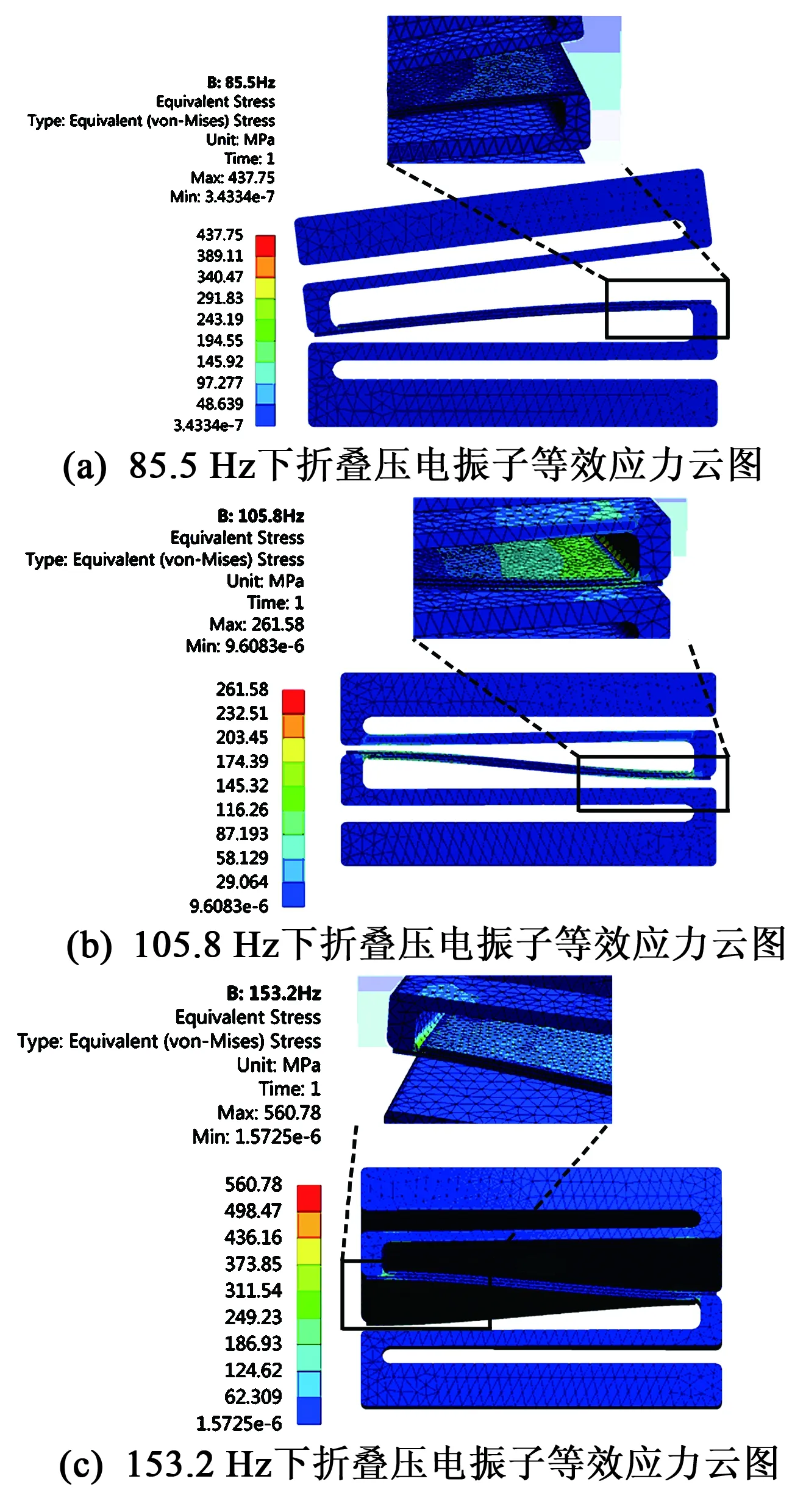
圖3 折疊壓電振子等效應力分布圖

由圖3可見，85.5 Hz時折疊壓電振子薄梁部分發生左、右橫向振動；105.8 Hz時薄梁部分發生上、下橫向振動，是常見的工作模式，彈性層的應力分布集中在兩端圓角的過渡位置，所處位置的應力值為203.45 MPa；153.2 Hz時薄梁部分發生扭轉振動。通過分析折疊壓電振子的應力變化，可得彈性層與壓電層隨粘結層厚度變化的應力曲線，如圖4、5所示。

圖4 彈性層應力隨粘結層厚度變化曲線

圖5 壓電層應力隨粘結層厚度變化曲線

彈性層的屈服強度為205 MPa。由圖4可見，彈性層分別在85.5 Hz、105.8 Hz，粘結層厚分別為0.03～0.10 mm及0.05～0.08 mm時，所受應力小于許用應力值，滿足彈性層抵抗微量塑性變形的要求。其中，當粘結層厚為0.07 mm時，彈性層在不同頻率下所受應力最小，當85.5 Hz時，彈性層應力值為175.34 MPa。

折疊壓電振子在頻率153.2 Hz的作用下，粘結層厚為0.07～0.08 mm。應力值接近彈性層的屈服強度，在長久的工作條件下，將使折疊壓電振子永久失效，無法恢復強度要求。

本文研究的折疊式壓電振子為中心對稱結構。由圖3可以看出，上下壓電層的應力大小相等，方向相反。當薄梁部分發生彎曲變形時，沿其長度方向的上下壓電層的應力表現為一側拉應力，另一側為壓應力。由圖5可以看出，折疊壓電振子在不同的工作模式下，粘結層厚度為0.06～0.08 mm時，壓電層的應力值最小。85.5 Hz時壓電層所受應力值為68.34 MPa。

因此，折疊壓電振子在不同的工作模式下，通過分析彈性層與壓電層的應力變化可知，當粘結層厚為0.07～0.08 mm，應力變化最小。為保證折疊式壓電振子能長時間工作，現對其進行疲勞壽命分析。

3 折疊式壓電振子的疲勞分析

本文選用nCode DesignLife軟件對折疊式壓電振子進行疲勞壽命分析。疲勞是結構在應力或應變的反復作用下發生破壞的現象。疲勞壽命是指結構發生破壞時，循環載荷作用的次數或時間。

將其靜力分析的結果傳輸到疲勞分析軟件中，選用時間載荷的應力-壽命模塊。彈性折疊梁的材料為304鋼，其應力-壽命疲勞特性曲線可通過nCode材料庫直接獲取；而壓電材料與粘結層在材料庫中無對應的應力-壽命曲線，可通過壓電材料的彈性模量(60 GPa)、拉伸極限強度(77 MPa)及粘結層的彈性模量(3.5 GPa)、拉伸極限強度(31 MPa)進行自定義，生成修正的應力-壽命曲線。

設置彈性層、壓電層和粘結層結構材料參數。設置正弦位移載荷幅值為1 mm，作用時間為1 s。經過疲勞壽命計算，在3種工作模式下折疊式壓電振子的壽命分布如圖6所示。

圖6 折疊式壓電振子壓電層的疲勞壽命分布

由圖6可見，折疊壓電振子在振動過程中，結構的疲勞破壞發生在壓電層。85.5 Hz下，結構發生左、右橫向振動，位于薄梁端部的壓電層的疲勞壽命次數為8.82×106。在常用的工作模式105.8 Hz時，薄梁部分發生上、下橫向振動，壓電層的破壞發生在中間薄梁圓角兩端的過渡位置，疲勞壽命次數為5.317×107。153.2 Hz下，薄梁部分發生扭轉振動，壓電層的疲勞壽命次數為1.624×106。在3種工作模式下，通過分析折疊壓電振子壓電層的疲勞壽命，得到壓電層隨粘結層厚度變化的疲勞壽命曲線(見圖7)。由圖7可知，當粘結層厚度在0.07～0.08 mm時，壓電層的疲勞壽命最高。在105.8 Hz時，其疲勞壽命次數可達107；而在85.5 Hz和153.2 Hz時，壓電層的疲勞壽命次數為106。這是因為在位移載荷下，薄梁部分發生左、右橫向振動和扭轉振動時，壓電層在薄梁部分兩端圓角的過渡位置產生應力集中，使疲勞壽命減小1個數量級。

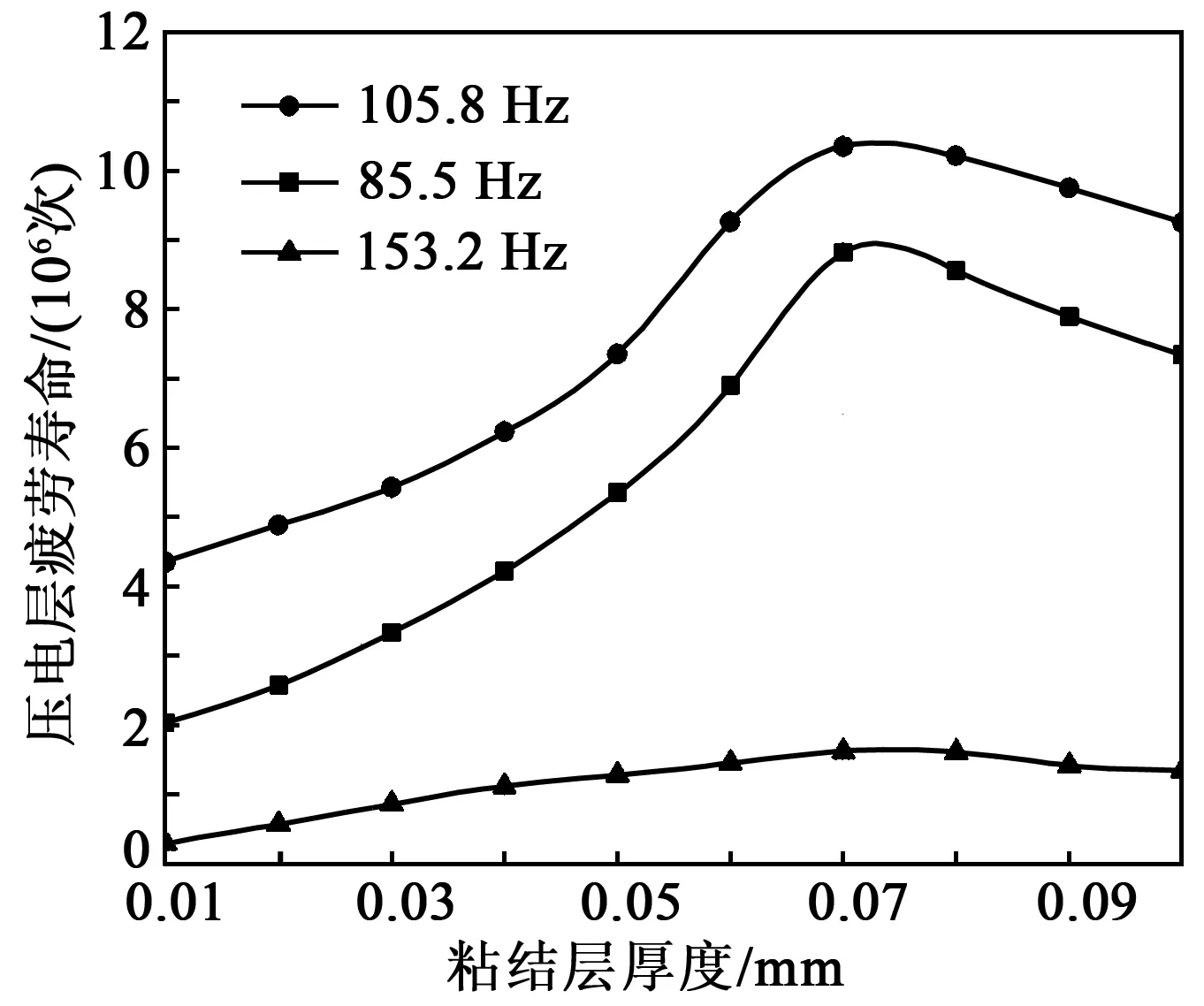
圖7 壓電層疲勞壽命與粘結層厚度的關系

4 結束語

本文對一種折疊式壓電振子的疲勞壽命進行了分析。通過對粘結層的理論分析，在3種不同工作的模式下施加位移載荷，討論了粘結層厚度對彈性層和壓電層的應力變化情況，并將結果傳輸到疲勞分析軟件中，得出折疊壓電振子壓電層的疲勞壽命分布云圖。經過分析，當粘結層厚為0.07 mm時，在第2種工作模式下(105.8 Hz)壓電層的疲勞壽命最高。

由此可見，粘結層厚度的變化和不同的位移載荷對壓電陶瓷的疲勞壽命影響很大。在實際應用中，折疊壓電振子應選擇適宜的粘結層厚度和正確的工作模式，綜合考慮壓電陶瓷的疲勞壽命，才能實現最大的電能輸出。