光纖陀螺溫變效應(yīng)誤差抑制方法研究

李 陽，黃 鑫，路彬彬，張登偉

(1. 南京電子技術(shù)研究所，江蘇 南京 210000；2. 浙江大學(xué) 光電科學(xué)與工程學(xué)院 現(xiàn)代光學(xué)儀器國家重點實驗室，浙江 杭州 310027)

0 引言

光纖陀螺(FOG)是慣性導(dǎo)航領(lǐng)域中的重要傳感器，其高精度、全固態(tài)、啟動快及動態(tài)范圍大等優(yōu)點符合當(dāng)前軍事應(yīng)用的需求。目前由于溫度場導(dǎo)致的非互易性零偏漂移誤差限制了光纖陀螺精度的進(jìn)一步提升[1-5]，Lefevre將這一現(xiàn)象稱為光纖陀螺溫變效應(yīng)誤差[6-7]，因此，解決這一問題已成為光纖陀螺進(jìn)一步發(fā)展的關(guān)鍵。

溫變效應(yīng)誤差的抑制方法有硬件優(yōu)化和軟件補(bǔ)償。硬件優(yōu)化主要通過改善熱結(jié)構(gòu)設(shè)計,增加溫控[8],采用新的光纖環(huán)繞法[9-10]和工作原理[11-12]等方法實現(xiàn)，但會帶來質(zhì)量、體積增加，工藝復(fù)雜，光纖環(huán)結(jié)構(gòu)強(qiáng)度下降等問題。軟件補(bǔ)償法易于工程實現(xiàn)，且抑制效果較好，其中線性誤差模型[13-15]易于工程應(yīng)用，但依賴于精確的誤差模型和溫度信息。采用神經(jīng)網(wǎng)絡(luò)等機(jī)器學(xué)習(xí)方法[16-17]可自適應(yīng)進(jìn)行最優(yōu)模型識別，但受限于機(jī)上/彈上計算機(jī)運(yùn)算資源，一般應(yīng)用于非實時的數(shù)據(jù)后處理場合。通過經(jīng)驗?zāi)B(tài)分解，結(jié)合曲面擬合回歸和自適應(yīng)模糊推理聯(lián)合建模的方法，可獲得較好的補(bǔ)償效果[18]。查表補(bǔ)償法[19]具有實現(xiàn)簡單，無需精確建模，實時性和補(bǔ)償效果好的優(yōu)點，具有很大的工程應(yīng)用潛力。

本文通過光纖陀螺溫變效應(yīng)誤差的原理分析與建模，提出基于查表法的啟動溫變效應(yīng)誤差抑制方法。通過實驗驗證其誤差抑制效果，提供了一種有效的實時工程應(yīng)用方案，對提升光纖陀螺的精度水平和系統(tǒng)應(yīng)用性能具有重要意義。

1 方法原理

1.1 光纖陀螺溫變效應(yīng)誤差模型

光纖陀螺溫變效應(yīng)誤差體現(xiàn)為光纖陀螺內(nèi)部溫度場變化時的輸出漂移誤差，由廣義Shupe效應(yīng)、標(biāo)度因數(shù)的溫度效應(yīng)和檢測通道的溫度效應(yīng)組成，其中后兩種效應(yīng)可通過標(biāo)度因數(shù)溫度標(biāo)定、半波電壓閉環(huán)控制和選擇低溫度系數(shù)電子元器件得到很好抑制。因此，光纖陀螺溫變效應(yīng)誤差主要來源為廣義Shupe效應(yīng)，其誤差模型如圖 1所示(圖中Δφs=Ω·Ko為薩格奈克相位差)，對應(yīng)光纖陀螺的輸出為

D=(Ω·Ko+Δφe)·Ke

(1)

式中：Ω為輸入旋轉(zhuǎn)角速率;Ko、Ke為光學(xué)、電學(xué)標(biāo)度因數(shù); Δφe為廣義Shupe效應(yīng)引起的加性溫變效應(yīng)相位誤差。

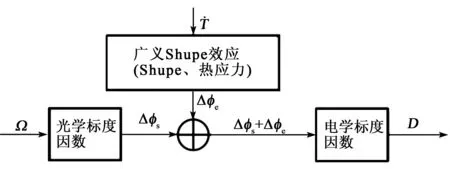
圖1 光纖陀螺溫變效應(yīng)誤差源

廣義Shupe效應(yīng)包括傳統(tǒng)的Shupe效應(yīng)及熱應(yīng)力效應(yīng)，具體表示為

z,t)]·(L-2z)dz

(2)

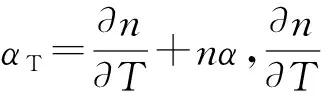
由式(2)可知，當(dāng)光纖環(huán)中相對光纖中點對稱位置的溫變速率相同時，即可消除廣義Shupe效應(yīng)誤差。目前工程上采用四極對稱繞法光纖環(huán)來抑制廣義Shupe效應(yīng)，但由于光纖直徑限制，各層光纖間并非理想的關(guān)于光纖環(huán)中點對稱，存在殘余的溫變效應(yīng)誤差，在高精度光纖陀螺中不可忽略。

1.2 光纖環(huán)等效非穩(wěn)態(tài)溫度場分析

已知各個時刻光纖環(huán)溫度場分布，即可根據(jù)式(2)得到溫變效應(yīng)誤差。光纖環(huán)各層光纖緊密纏繞，可看作一個性質(zhì)均勻的整體，其主要的熱傳遞方式是熱傳導(dǎo)。同時光纖環(huán)熱分布為環(huán)形對稱形式，且在軸向上均勻分布，可只針對光纖環(huán)截面進(jìn)行二維熱傳導(dǎo)分析。建立簡化的一維光纖環(huán)分析模型如圖 2所示。圖中，d為光纖環(huán)光纖截面寬度，內(nèi)壁、外壁分別位于面向熱源和背向熱源的一側(cè)。

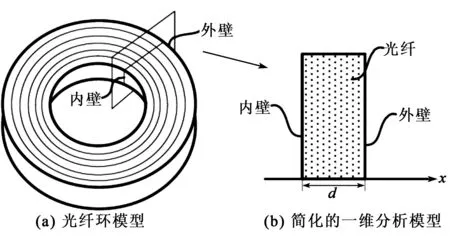
圖2 簡化一維光纖環(huán)分析模型

對于系統(tǒng)應(yīng)用中的光纖陀螺，光纖環(huán)外部還包含有隔熱層、外殼結(jié)構(gòu)及外部的系統(tǒng)結(jié)構(gòu)，可等效為多個導(dǎo)熱特性不同介質(zhì)層的疊加并看作一個整體。光纖陀螺啟動后在有限時間段內(nèi)，光纖環(huán)內(nèi)表面所受熱作用可看作只滲透到有限厚度范圍內(nèi)，可等效為“半無限大物體”，對應(yīng)的等效模型如圖 3所示。圖中R為光纖環(huán)內(nèi)側(cè)半徑。

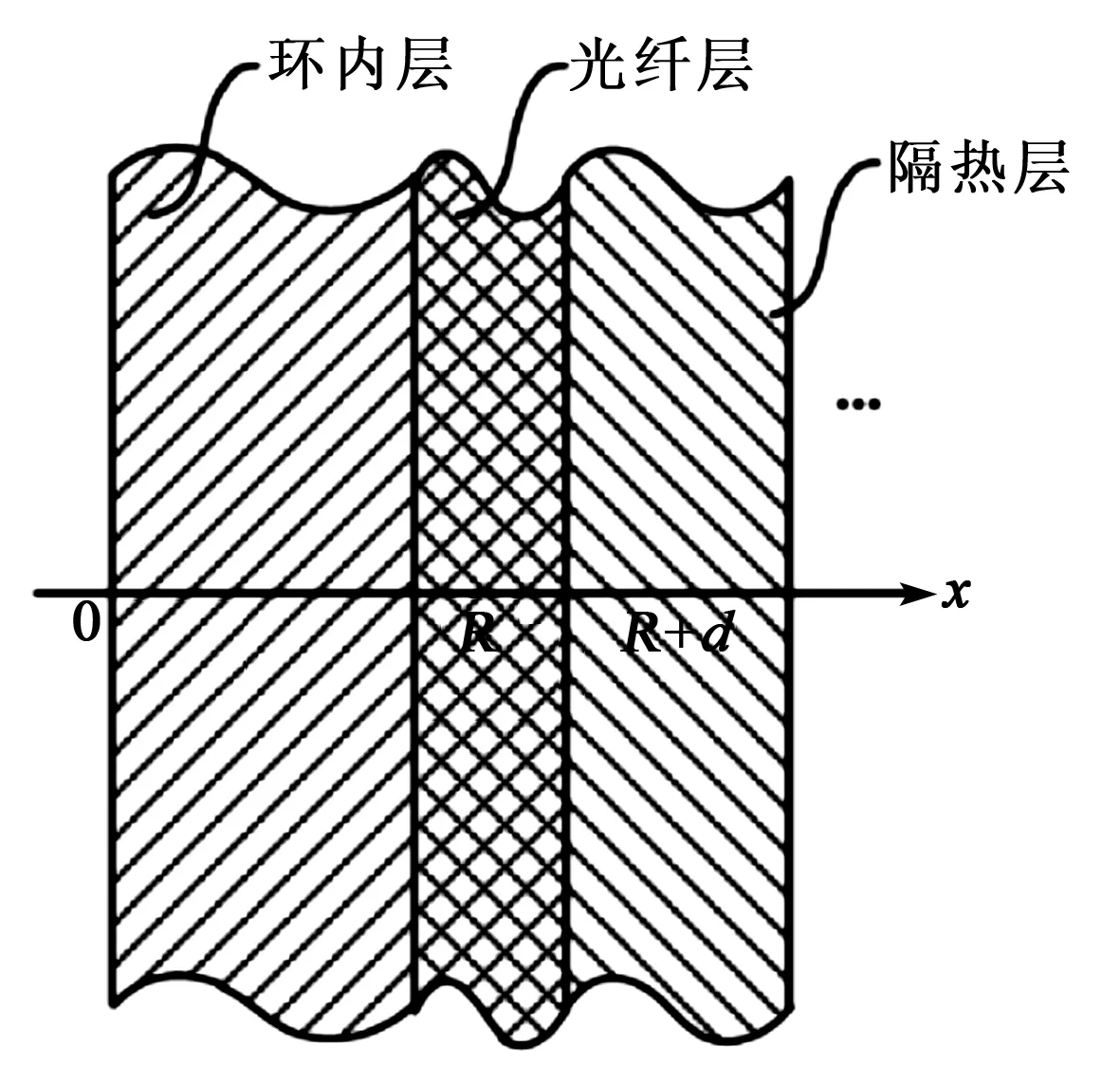
圖3 光纖環(huán)半無限大物體等效分析模型

光纖陀螺初始溫度為T0，啟動時x=0位置處的邊界溫度突然提高到Tw并保持不變。引入過余溫度θ=T-T0(T為光纖環(huán)內(nèi)的溫度)，結(jié)合一維導(dǎo)熱微分方程獲得光纖環(huán)非穩(wěn)態(tài)導(dǎo)熱問題的數(shù)學(xué)描述為

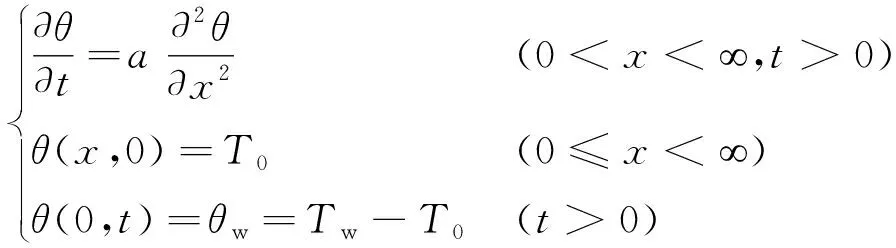
(3)

式中：a為熱擴(kuò)散系數(shù)；t為時間。初始條件為T(x,y,z,0)=T0。式(3)的解為

(4)

各個位置處溫度的時間梯度為

(5)

將式(5)代入式(2)可獲得光纖陀螺啟動過程的溫變效應(yīng)誤差模型，下面基于四極對稱光纖環(huán)進(jìn)行誤差模型的推導(dǎo)與查表法抑制原理的闡述。

1.3 光纖陀螺溫變效應(yīng)查表法抑制原理

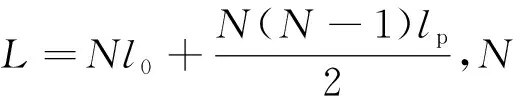
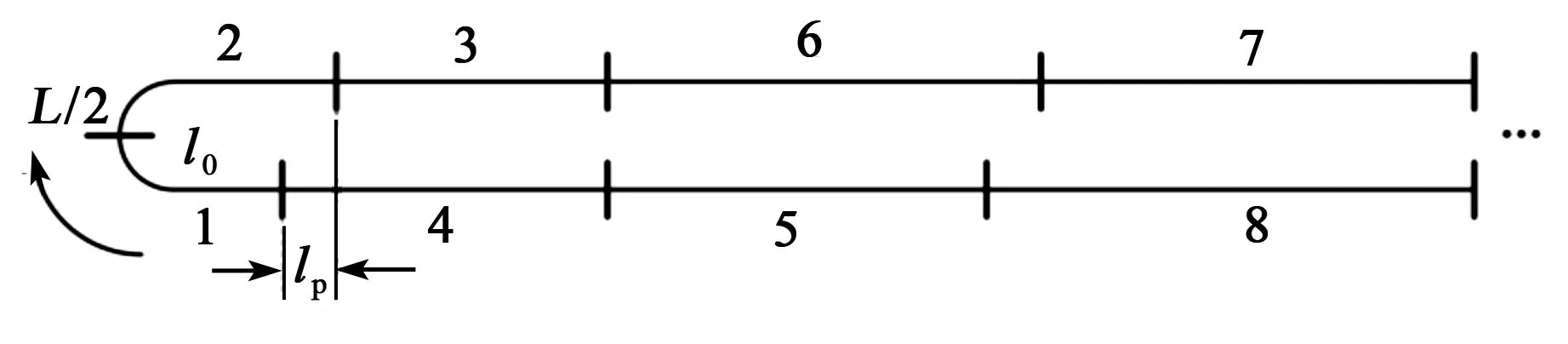
圖4 四極對稱繞法光纖環(huán)層分布示意圖

根據(jù)式(2)可得離散化廣義Shupe誤差為

[lend(q,m)-lstart(q,m)]·

[L-lend(q,m)-lstart(q,m)]

(6)

式中l(wèi)start(q,m)，lend(q,m)分別為第q個極子中第m層光纖的起點與終點坐標(biāo)。將常數(shù)項進(jìn)行合并可得：

(7)

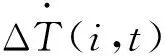
根據(jù)式(5)可得溫度時間梯度為時間t的單一變量函數(shù)：

(8)

可將式(7)進(jìn)一步寫為

(9)

因此，光纖陀螺啟動過程的溫變效應(yīng)導(dǎo)致的相位誤差為時間t的復(fù)雜函數(shù)，幅值由θw決定。在不同啟動溫度環(huán)境下，光纖陀螺內(nèi)部熱源不同的發(fā)熱功率對應(yīng)不同的邊界過余溫度，因此，幅值θw取決于啟動時的環(huán)境溫度T0。在不同啟動溫度環(huán)境下，溫變效應(yīng)誤差具有相同時間變化趨勢，只是具有不同的幅值。因此式(9)可改寫為

Δφe(t)=θw(T0)·f(t)

(10)

式中：θw(T0)為溫變效應(yīng)誤差幅值系數(shù)；f(t)為溫變效應(yīng)誤差時間函數(shù)。

基于上述分析，可確定光纖陀螺啟動溫變效應(yīng)誤差的查表法抑制原理：通過實驗獲得不同標(biāo)定啟動環(huán)境溫度Ti下的光纖陀螺啟動溫變效應(yīng)誤差，采用時間表格方法建立式(10)形式的時間函數(shù)F(t,Ti)。在光纖陀螺啟動時，按照啟動環(huán)境溫度T和啟動時間查詢對應(yīng)的時間表格，獲得對應(yīng)溫變效應(yīng)誤差，并在光纖陀螺輸出數(shù)字量中加以補(bǔ)償，從而實現(xiàn)啟動溫變效應(yīng)誤差的抑制。

實際工程應(yīng)用中，T≠Ti，根據(jù)溫變效應(yīng)誤差模型可認(rèn)為在一定溫度范圍內(nèi)θw與環(huán)境溫度成線性關(guān)系，此時可以取相鄰最近的兩個溫度標(biāo)定點Ti和Ti+1下的時間表格F(t,Ti)和F(t,Ti+1)，根據(jù)溫度值進(jìn)行等比例插值獲得T下的時間表格為

F(t,Ti)

(11)

1.4 光纖陀螺溫變效應(yīng)誤差評價方法

為對溫變效應(yīng)誤差抑制效果進(jìn)行評估，需要統(tǒng)一的方法對誤差進(jìn)行量化。可參考慣導(dǎo)系統(tǒng)的圓概率誤差(CEP)精度評估方法[20]，計算光纖陀螺的漂移概率誤差(DEP)。對光纖陀螺數(shù)據(jù)進(jìn)行角度積分，將積分結(jié)果歸化至1 h，獲得每個采樣時刻ti的漂移率為

(12)

式中θ(ti)為ti時刻的角度積分值。

ΩER服從均值為0，標(biāo)準(zhǔn)差為σ的一維正態(tài)分布，漂移概率誤差ΩDEP(95%)為1.96σ，σ使用漂移率標(biāo)準(zhǔn)差估計值代替。光纖陀螺的漂移概率誤差計算過程中使用角度積分值進(jìn)行計算，避免了白噪聲的影響，可直接量化評估溫變效應(yīng)誤差。

另外,慣導(dǎo)系統(tǒng)的位置精度是反映其性能的重要指標(biāo)，而光纖陀螺的漂移誤差會直接導(dǎo)致導(dǎo)航的位置誤差，因此，可直接采用系統(tǒng)位置誤差進(jìn)行誤差評估。將光纖陀螺漂移數(shù)據(jù)代入導(dǎo)航解算過程，導(dǎo)航結(jié)果中僅包含有光纖陀螺漂移所帶來的導(dǎo)航誤差。根據(jù)慣導(dǎo)系統(tǒng)精度評定方法獲得導(dǎo)航圓概率誤差，反映了溫變效應(yīng)誤差對系統(tǒng)誤差的貢獻(xiàn)。

綜上所述，光纖陀螺漂移概率誤差與慣導(dǎo)系統(tǒng)圓概率誤差是溫變效應(yīng)誤差的有效量化評估手段。在后續(xù)的實驗數(shù)據(jù)分析中，采用DEP與系統(tǒng)CEP對溫變效應(yīng)誤差進(jìn)行評估。

2 實驗結(jié)果與分析

實驗中，采用溫箱控制環(huán)境溫度進(jìn)行-40～+60 ℃的環(huán)境溫度控制。溫箱放置在隔振地基上，光纖陀螺靜態(tài)放置于溫箱內(nèi)部。光纖陀螺采用穩(wěn)壓電源進(jìn)行供電，輸出數(shù)據(jù)通過串口發(fā)送至上位機(jī)，通過數(shù)據(jù)采集軟件進(jìn)行光纖陀螺輸出數(shù)據(jù)的接收。整體實驗裝置示意圖如圖 5所示。

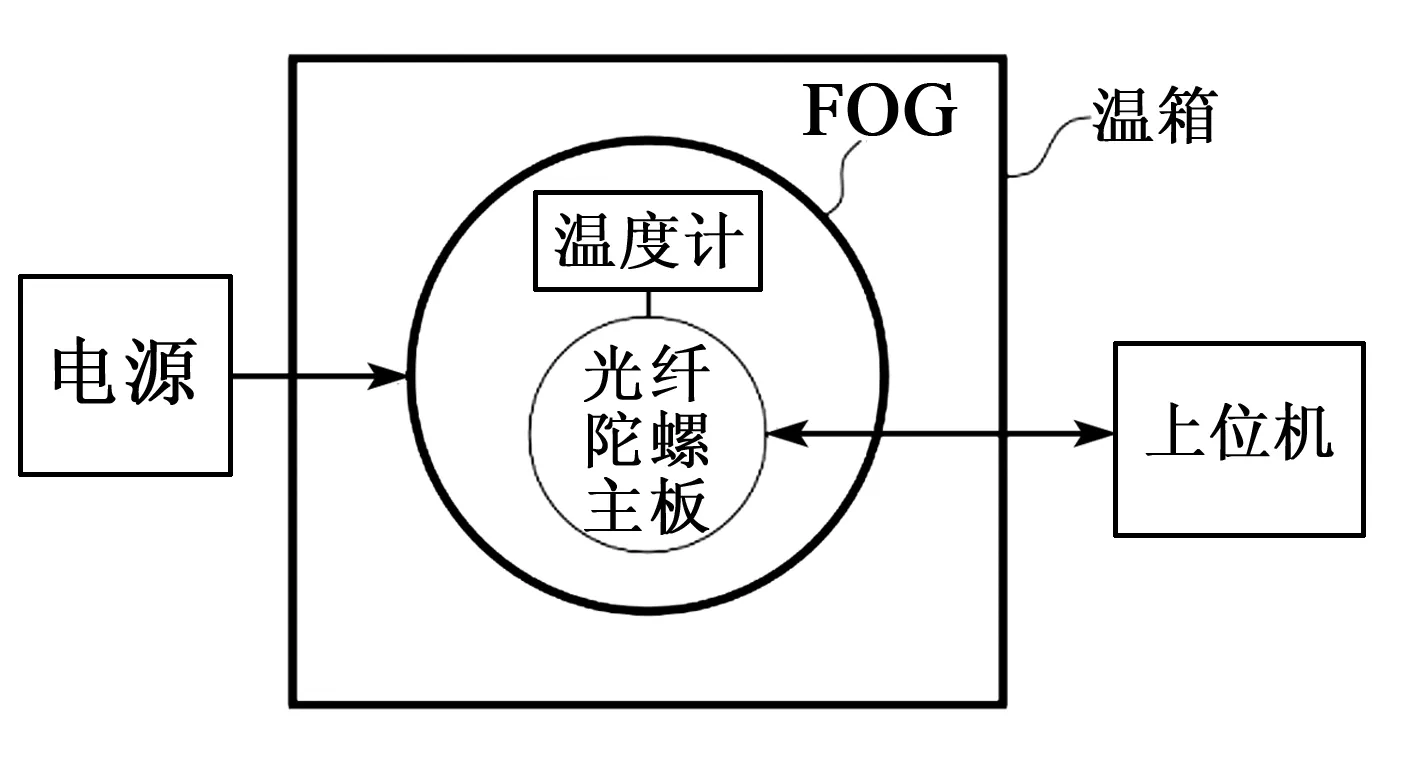
圖5 實驗裝置示意圖

為獲得各個啟動溫度下的光纖陀螺啟動溫變效應(yīng)抑制表格，同時驗證各溫度點下光纖陀螺啟動溫變效應(yīng)誤差查表法抑制效果，進(jìn)行零狀態(tài)重復(fù)啟動實驗。設(shè)置一固定的環(huán)境溫度，對陀螺進(jìn)行斷電4 h、通電2 h的啟動測試，每個溫度測試4組數(shù)據(jù)。在每個溫度點下，對多組啟動數(shù)據(jù)按照時間點進(jìn)行平均后進(jìn)行中心滑動平均，獲得一組噪聲抑制后的光纖陀螺零狀態(tài)啟動趨勢數(shù)據(jù)。根據(jù)第1.1節(jié)中光纖陀螺溫變效應(yīng)理論，當(dāng)光纖陀螺內(nèi)部溫度場達(dá)到穩(wěn)態(tài)時，其溫變效應(yīng)誤差為0，因此，可以認(rèn)為光纖陀螺啟動測試數(shù)據(jù)中末段為不包含溫變效應(yīng)誤差的輸出。將光纖陀螺零狀態(tài)啟動數(shù)據(jù)減去數(shù)據(jù)末段的平均值，即獲得該溫度點下光纖陀螺溫變效應(yīng)誤差抑制表格，流程如圖 6所示。

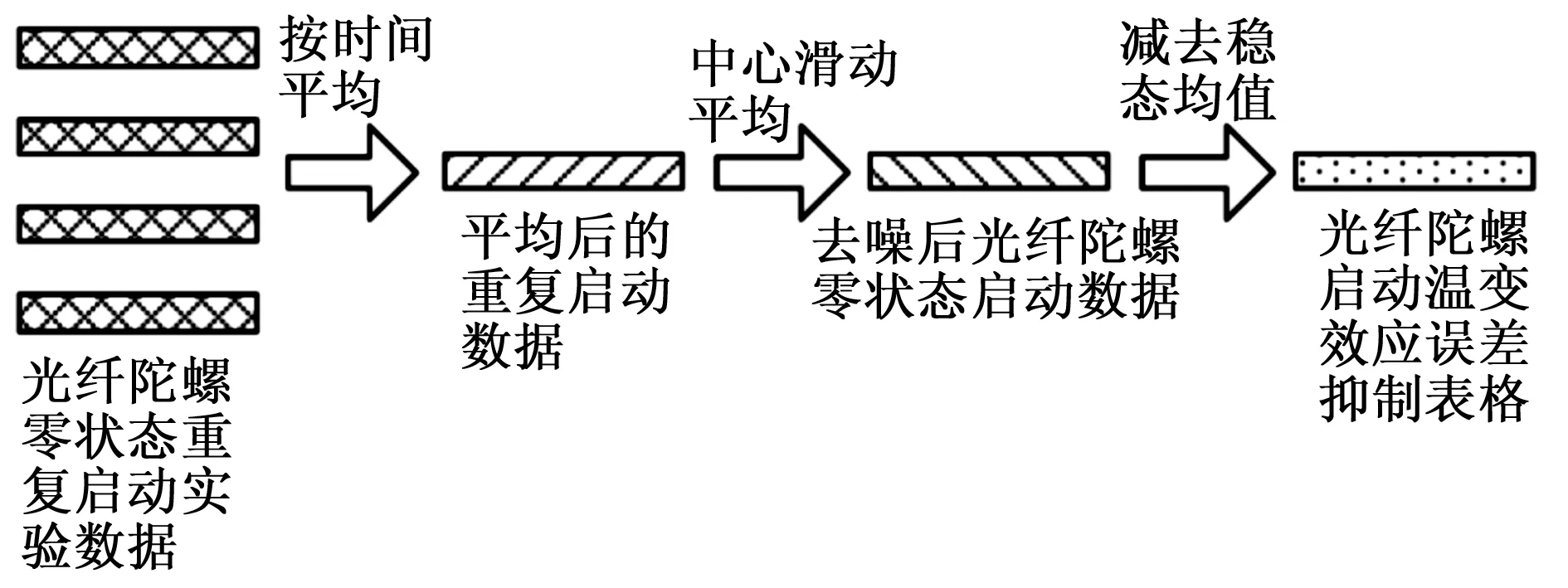
圖6 誤差抑制表格計算流程

根據(jù)誤差抑制表格，對光纖陀螺零狀態(tài)啟動輸出數(shù)據(jù)進(jìn)行實時溫變效應(yīng)誤差抑制。圖 7為20 ℃條件下誤差抑制前、后的光纖陀螺啟動數(shù)據(jù)對比。

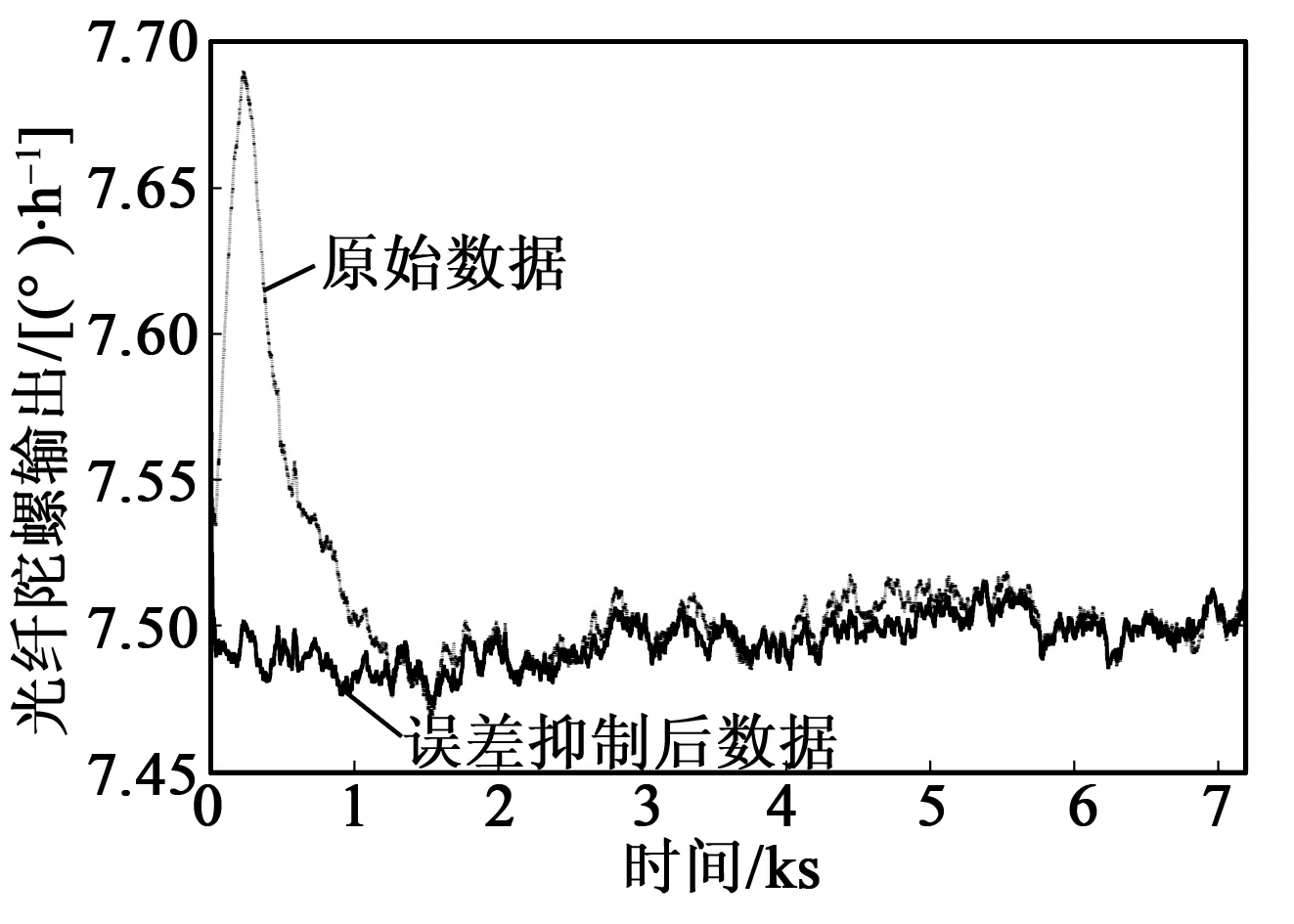
圖7 20 ℃環(huán)境下誤差抑制前、后對比

根據(jù)第1.4節(jié)中的溫變效應(yīng)誤差評價方法計算誤差抑制前、后的DEP和導(dǎo)航CEP，如表 1所示。誤差抑制后DEP由0.10～0.12 (°)/h下降為0.004～0.006 (°)/h，誤差剩余比小于6%。導(dǎo)航CEP從7～9 n mile/h降至0.5 n mile/h以下，誤差剩余比小于7%。同時DEP指標(biāo)與導(dǎo)航CEP指標(biāo)成正相關(guān)。

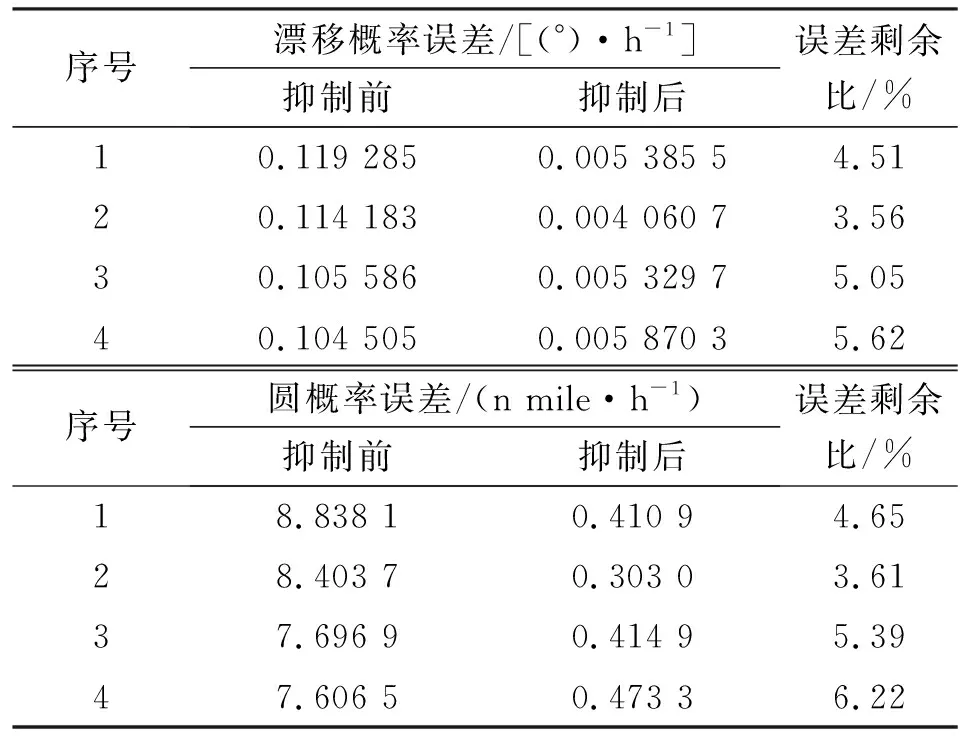
表1 20 ℃條件下誤差抑制前、后的漂移概率誤差與導(dǎo)航圓概率誤差

為驗證光纖陀螺溫變效應(yīng)誤差模型在全溫范圍內(nèi)的適應(yīng)性，進(jìn)行了全溫條件下的光纖陀螺溫變效應(yīng)誤差抑制實驗。以10 ℃為間隔，在-40～60 ℃設(shè)置11個環(huán)境溫度點進(jìn)行光纖陀螺靜態(tài)啟動測試，測試時間為2 h。實驗中，每次溫箱調(diào)整溫度后，對陀螺進(jìn)行大于4 h的冷卻，以保證陀螺內(nèi)部溫度場充分穩(wěn)定。各個環(huán)境溫度點下的測試數(shù)據(jù)表明，光纖陀螺溫變效應(yīng)誤差在不同環(huán)境溫度下的幅值不同，通過各個溫度下的光纖陀螺啟動溫變效應(yīng)誤差抑制表格加以補(bǔ)償后，溫變效應(yīng)誤差下降較大。計算各個溫度點下誤差抑制前、后光纖陀螺的DEP與導(dǎo)航CEP指標(biāo)，如圖 8所示。

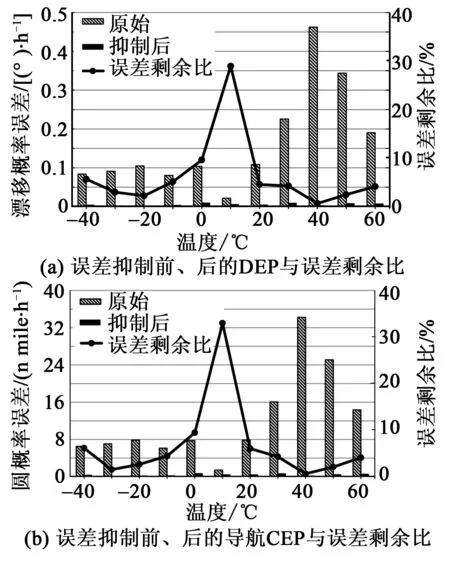
圖8 全溫條件下誤差抑制前、后實驗結(jié)果

由圖8(a)可看出，溫變效應(yīng)誤差模型在不同溫度下的光纖陀螺DEP抑制效果不同，在40 ℃下抑制比最高，DEP誤差剩余比為0.63%，而10 ℃下抑制比最低，DEP誤差剩余比為28.94%。在10 ℃下，光纖陀螺自身的溫變效應(yīng)誤差較小，原始光纖陀螺數(shù)據(jù)DEP為0.021 424 (°)/h，經(jīng)過誤差抑制后為0.006 200 (°)/h，因此，誤差抑制比較小。對比圖 8(b)、(a)可看出，導(dǎo)航CEP指標(biāo)溫度分布與光纖陀螺DEP指標(biāo)相似，且兩者誤差剩余比也具有相同的趨勢。在全溫范圍內(nèi)，光纖陀螺DEP從0.02～0.5 (°)/h下降到小于0.01 (°)/h，而對應(yīng)的導(dǎo)航CEP從1.4～35 n mile/h下降到小于0.8 n mile/h。

實驗結(jié)果表明，通過應(yīng)用光纖陀螺溫變效應(yīng)誤差抑制法，常溫條件下光纖陀螺DEP從0.10～0.12 (°)/h降至為0.004～0.006 (°)/h，對應(yīng)導(dǎo)航CEP從7～9 n mile/h降至0.5 n mile/h以下；在全溫度范圍內(nèi)，光纖陀螺DEP從0.02～0.5 (°)/h降至0.01 (°)/h以下，導(dǎo)航CEP從1.4～35 n mile/h降至小于0.8 n mile/h。該方法對光纖陀螺的溫變效應(yīng)誤差具有有效的抑制作用，具有良好的一致性與全溫度范圍內(nèi)的適應(yīng)性，可有效降低由于溫變效應(yīng)導(dǎo)致的光纖陀螺漂移誤差，提升對應(yīng)導(dǎo)航系統(tǒng)精度。

3 結(jié)束語

本文根據(jù)光纖陀螺溫變效應(yīng)誤差機(jī)理，結(jié)合光纖環(huán)等效非穩(wěn)態(tài)溫度場分析，獲得了啟動狀態(tài)下溫變效應(yīng)誤差等效數(shù)學(xué)模型。等效數(shù)學(xué)模型中的幅值系數(shù)僅與環(huán)境溫度有關(guān)，并對于狀態(tài)固定的光纖陀螺其時間函數(shù)保持不變，根據(jù)這一特點提出了基于查表法的光纖陀螺溫變效應(yīng)誤差抑制方法。同時根據(jù)光纖陀螺的數(shù)據(jù)特征與系統(tǒng)應(yīng)用特點，提出了采用漂移概率誤差和導(dǎo)航圓概率誤差對溫變效應(yīng)誤差進(jìn)行量化評估。開展了全溫條件下溫變效應(yīng)誤差抑制實驗，實驗中獲得了90%以上的誤差抑制效果，全溫環(huán)境下系統(tǒng)導(dǎo)航定位誤差從最大34.221 3 n mile/h降至0.730 4 n mile/h。實驗結(jié)果表明，通過該文誤差抑制方法的應(yīng)用，有效抑制了光纖陀螺溫變效應(yīng)誤差，提升了相應(yīng)的系統(tǒng)性能，具有很強(qiáng)的工程應(yīng)用價值。

此外，當(dāng)考慮更惡劣的應(yīng)用環(huán)境時，外界環(huán)境為變溫條件，根據(jù)溫變效應(yīng)誤差模型，其內(nèi)部的熱傳導(dǎo)過程相當(dāng)于一個時變邊界條件的傳熱過程，若仍采用固定溫度下的誤差抑制表格會導(dǎo)致較大的剩余誤差。此時可通過標(biāo)定獲得的環(huán)境溫度與誤差抑制表格幅值系數(shù)間的關(guān)系，根據(jù)外界環(huán)境溫度實時調(diào)整幅值系數(shù)，以逼近變溫條件下的溫變效應(yīng)誤差。變溫條件下的溫變效應(yīng)誤差抑制，需要進(jìn)一步試驗研究，是后續(xù)研究的重點方向。