一種基于改進粒子群的多小區天線聯合優化算法

胡其美 曹蘋 林侃 王邦

【摘 ?要】

針對基站天線參數調優問題，提出了一種用于在龐大離散空間中搜索最優解的優化算法，該算法借鑒了粒子群算法的基本概念，分為三個步驟。第一步為隨機篩選，挑選出一批較為優秀的個體組成粒子群;第二步為大步長調節，通過大范圍搜索提高尋優效率;第三步為小步長調節，在迭代時只做細微調節進行局部查找，最終能找到最優解。通過直接操作場強矩陣計算綜合覆蓋率，得到最佳覆蓋率時對應的天線參數組合，從而給多小區聯合調優提供指導。實驗證明該算法能夠在多小區聯合優化中取得良好的效果。

【關鍵詞】最優解;天線參數;粒子群算法

[Abstract]

Aiming at the parameter tuning problem of base station antenna， this paper proposes an optimization algorithm for searching the optimal solution in the large discrete space. The algorithm borrows the basic concept of particle swarm algorithm and is divided into three steps. The first step is random selection， and a group of relatively good individuals are selected to form a particle group; the second step is the large-step adjustment， and the optimization efficiency is improved by a wide range search; the third step is the small-step adjustment to perform fine adjustments for local search and eventually find the optimal solution. The comprehensive coverage probability is calculated by directly operating the field intensity matrix， and the corresponding antenna parameter combination is obtained， thereby providing guidance for multi-cell joint tuning. Experiments show that the algorithm can achieve good results in multi-cell joint optimization.

[Key words]optimal solution; antenna parameter; particle swarm optimization

0 ? 引言

通信網絡的架設和參數調整是一項耗時和艱巨的任務，需要權衡各種因素，使得網絡在滿足一定需求的條件下成本盡量降低。在移動網絡的覆蓋中，需要綜合調整小區天線的各項參數，使目標區域的信號質量滿足通信需求。各區域地貌不同，所以沒有通用的參數調整方案，實際工作中往往需要根據工程師的經驗來進行調整，并通過路測來檢驗信號質量。

高效的天線參數優化算法能直接計算得到天線的各項參數指標，將能減少資源消耗。在這方面，已有一些前期研究：夏永康等人提出了一種基于黃金分割搜索的針對能效的天線下傾角自優化算法[1];潘如君等人提出了一種基于改進粒子群的天線下傾角調整方案，該方案通過調整基站的天線傾角來優化網絡覆蓋[2];史黛君等人提出了一種基于權值的TD-LTE天線覆蓋優化方法，主要通過調整天線主瓣方向角來優化[3]。這些方法都取得了一定效果但只考慮到單一因素，而在建筑密集地區，由于天線間相互影響，需要綜合考慮天線的各項因素，單獨調整某個參數不能取得良好結果。谷欣杏等人提出了一種基于遺傳算法的LTE網絡覆蓋優化方法[4];張捷等人提出了一種基于模擬退火算法的移動通信網絡自規劃方法[5]，這些方法考慮全局優化的情況，采用啟發式搜索方法來提升網絡性能。本文在這些研究的基礎上，提出了一種基于改進粒子群算法的全局天線參數優化方法，通過建立目標區域網絡模型，以網絡覆蓋質量為優化目標，通過降低重疊覆蓋和弱覆蓋等指標以提高網絡質量。

1 ? 模型及背景

1.1 ?問題建模

將待優化的目標區域P網格化為指定寬度的x×y的柵格陣列，整個網格的柵格表示為G={g1， g2， …， gr}，其中，r=x×y，則目標區域可以用一個矩陣M來描述，柵格的某個具體位置表示為Mij，坐標為（xi， yi）。網絡中的一根天線覆蓋的小區可表示為維度小于M的子矩陣，所有小區表示為C={c1， c2， …， cncell}，其中，ncell為目標區域中小區的個數。在人口稠密的城市區域，優化一片區域時不能忽略周圍區域天線帶來的影響，所以考慮到周圍區域的影響，柵格區域為g' ={g1'， g2'， …， gr' }，其中，r'=x'×y'，x'和y'是考慮到受影響的目標區域外圍之后的柵格陣列大小，其模型如圖1示，黑色邊框包圍的部分為目標區域大矩陣，綠色覆蓋區域為一根天線覆蓋下的子矩陣（為保持圖片清晰，示意圖中柵格劃分比實際大）。每個基站配備3個天線，每個天線的可調參數如圖中標注，包括高度H，下傾角D，方向角A。

1.2 ?考慮的網絡覆蓋指標

評估LTE系統網絡質量的指標有SINR、RSRP、上行下行速率、綜合覆蓋率等指標，其覆蓋類指標中的弱覆蓋率和重疊覆蓋率是一對相互矛盾的指標。出現弱覆蓋的柵格區域會直接導致用戶無法完成通訊需求;出現重疊覆蓋的區域會降低用戶體驗。二者直接影響到用戶能否進行正常的通訊，如何調整天線使其同時達到最優是無線網絡優化的核心問題。弱覆蓋率與重疊覆蓋率的定義如下：

（1）弱覆蓋率

弱覆蓋率定義為待優化目標區域中弱覆蓋的柵格數目在所有柵格中的占比，一個柵格被判定為弱覆蓋的定義為：目標區域中每根天線到該柵格的RSRP都小于-110 dBm。

（2）重疊覆蓋

重疊覆蓋率表示為待優化目標區域中重疊覆蓋的柵格數目在所有柵格中的占比，一個柵格滿足以下條件時被判定為重疊覆蓋柵格goverlap：一根天線到該柵格的RSRP大于-100 dBm;這樣的天線數目達到了3個及以上;該柵格最強場強的值與其他場強值相差在6 dBm以內，即|max（gmin）–gother|<6。

1.3 ?需要調整的天線參數指標

天線的調整指標包括站高、方向角、下傾角，這些指標同時影響目標區域的網絡覆蓋質量，在實際中不可能做到對每一個項參數的調整都無比精確。實際工作中，一般規定某種調整粒度，然后在一定范圍內根據該粒度進行調整，表示為：

其中，H、D、A分別表示可選的天線高度、下傾角、主瓣方位角的集合，hn、dn、an分別為集合中對應可調整的項數。

2 ? 算法

粒子群優化（PSO）算法是一種基于群體智能的全局搜索算法，最初由Kennedy J和Eberhart R提出[6]，源于對鳥群捕食行為的研究。它的基本思想是利用群體中的個體對信息的共享，使得整個群體的運動在問題求解空間中產生從無序到有序的演化過程，從而獲得問題的最優解。該算法最初只適用于求解連續的非線性函數優化問題。粒子具有位置和速度兩種屬性，通過粒子不斷往群體最佳位置和自身歷史最佳位置聚集，形成一種趨同效應，這導致其容易收斂到局部最優[7];算法的性能也依賴于其初始化的情形[8]，因此Richard提出了一種基于CVTs的種群初始化方法[9];薛明志等人提出一種正交設計方法對種群進行初始化[10];Maurice Clerc提出采用均勻隨機分布來初始化[11]。

對于離散問題，首先是Kennedy提出了一種針對0-1規劃的二進制PSO算法[12]。本文針對天線優化模型，直接將高維空間連續取值按照實際需求離散化。該算法本身是針對單目標優化問題，本文解決的是多目標問題，因此采用Zadeh提出的權重和方法（Weight-Sum Approach），為每個目標函數分配權重并將其組合為一個目標函數，將多目標轉化為單目標進行求解。可表示如下：

本文基于基本粒子群算法提出兩種改進方案，試驗結果表明，所提改進方案取得了良好的效果。

2.1 ?標準粒子群算法

假設一個種群有n個粒子，一個粒子的位置抽象為問題在解空間的一個解，解空間為搜索維度為D，對應為解空間D。粒子的位置Xi=（Xi1， Xi2， … ， Xid） （i=1， 2， …， n）表示粒子在搜索維度中的位置。Vi=（Vi1， Vi2， … ， Vin） （i=1， 2， …， n）表示粒子的速度。xbesti（i=1， 2， …， n）表示第i個粒子所經歷過的最佳位置，gbesti（i=1， 2， …， n）表示整個群體所有粒子中所經歷過的最佳位置，其數學表達式可表示為：

其中，w為慣性權重因子，c1、c2為學習因子，r1、r2為權重系數。w較低時會加速收斂，較高時會使粒子探索到解空間更多位置;c1r1決定了粒子飛向自身歷史最佳位置的步長;c2r2決定了粒子飛向全局最佳位置的步長。t表示本次迭代時的結果，t+1表示下一次迭代的結果。每次經過迭代得到新的粒子群時，其核心步驟為：

（1）評估當前每一個粒子的適應值;

（2）更新個體最佳位置和全局最佳位置;

（3）更新每個粒子的速度和位置。

其中粒子的適應值通常對應實際問題中的目標函數，即當前解對應的目標函數的值，根據當前解與期望值的差距來更新最佳位置。重復以上三個步驟直到停止條件滿足，停止條件一般為適應值達到期望值或者迭代次數達到上限。

2.2 ?改進算法一

標準粒子群算法的實驗表明直接在離散問題中的應用性能很差，因此本文基于粒子群優化方法的種群和粒子概念，基于時間效率考慮，去掉了離散版本標準粒子群算法迭代之后的速度變換過程，通過直接對粒子位置的調整獲得最優解，其調整結合天線自身的參數分布規律，極大地提高了尋優效率。算法分為兩步：

（1）第一步為初始化。首先隨機初始化一組粒子組成粒子群，計算每個粒子的適應值，然后每次隨機產生一個粒子A，當A的適應值大于原來種群中擁有最差適應值的粒子B時，用B替換掉A。經過一定次數的替換之后，得到一個每個粒子都有較優適應值的基礎群。因為每個粒子是隨機初始化產生的，所以相互之間在搜索空間中應該都相隔一定距離，為后續優化提供了空間，從而避免陷入局部最優。

（2）第二步為尋優過程。每次迭代時對每個個體的一個參數（對應一組解中的一根天線參數）做出調整，如果變好則更新，如果變差則下一組。一個解為一組天線的參數組合（N個天線，每個天線的一種參數配置）。由多個粒子組成一個種群（多組解），這個種群中的當前具有最佳適應值的粒子對應算法中的“全局最佳粒子”;對于種群中的每個粒子，其在歷次迭代中所經歷過的具有最佳適應值的粒子對應算法中的“個體最優粒子”。

實際中算法二的尋優效果比經典粒子群算法要好，但仍然存在尋優過程效率較低，運行時間長的缺點。

2.3 ?改進算法二

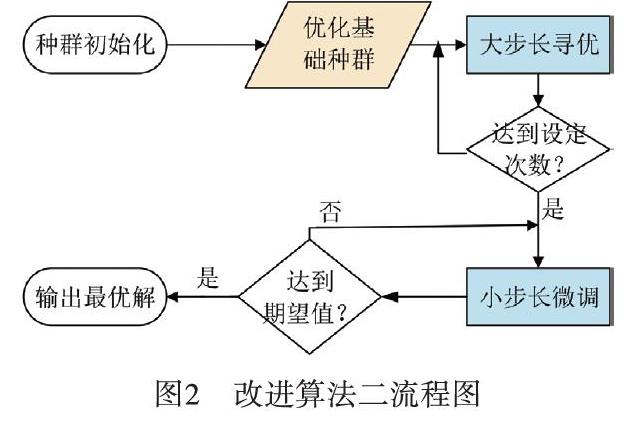
針對該算法第2步做一些改進，提出算法二。算法二先經過初始化之后，尋優過程主要分為三步，將算法一的第二步改為兩個步驟，第一個步驟為大步長調節，即對一組解的每一個天線都會做出調整，這樣就增大了搜索效率;第二個步驟為小步長調節，只對其中個別天線的參數進行變化，這樣就保證了效率與準確度兼備。其算法流程如圖2所示：

（1）初始化步驟同算法一。

（2）大步長調節。每次進行參數調整時讓每個天線參與調整（相當于增大原算法中的調節步長），由于參數組合列表是按照高度、下傾角、方向角分別在可行范圍內掃描得到的順序序列，相鄰可選數據組合必定是最終覆蓋效果相近的，所以只需要在原來天線參數的附近選擇即可。例如假設原來的天線組合為第m種，則下一次選擇時選取m-1或者m+1種。這樣可以在較短時間內找出較為滿意的種群，即期望值較高的多組解。

（3）小步長調節。局部查找，每次迭代值對每個個體的一個參數（對應一組解的一根天線參數）做出調整，如果變好則更新，如果變差則選擇下一組。

3 ? ?實驗

3.1 ?小規模場景

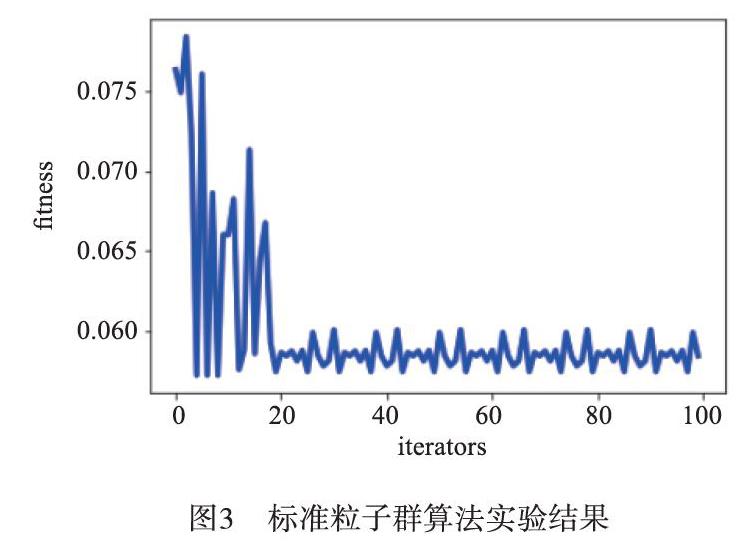
以河南省鄭州市某區域天線基站的實際測量數據為例，首先驗證算法在小規模數據集的效果。所選數據集的基站數目為3，每個基站架設有3根天線，天線參數調節范圍為：高度25～35 m，步長為5 m;下傾角0～8°，步長為4°;方向角0～330°，步長為30°。給定的數據是對應參數組合下的場強數據集合，一組參數對應一個場強數據的csv文件。每一個文件包含大約4萬條數據，每條數據中的有效項為x坐標，y坐標以及場強值三項，即對應大約200×200個格點的矩陣，每個格點有一個場強值。由于不同站點覆蓋的坐標范圍不同，為方便后續計算，需要將每個文件的數據映射到最小公共矩陣（所有站點覆蓋范圍的并集，取包含該并集的最小矩陣），將x坐標和y坐標映射為從0開始計數的序列（例如假設x的最大范圍是742490～748030，某個csv文件中x坐標范圍為742530～746510，則x的坐標范圍映射為2～201）。設置種群中個體數目為30（一個個體即為一組參數組合），初始時隨機選擇每個天線的一種參數組合（目標函數為0.075%，計算一次耗時約1 s），迭代100次，耗時52 min。其結果如圖3所示，在20多次（10 min左右）后目標函數基本收斂到定值，達到0.05%，下降了約30%。

3.2 ?大規模場景

在大規模數據集下，上述標準PSO算法由于粒子頻繁超出尋優空間而無法使用，而改進的算法則能達到目的。同樣以河南省鄭州市的實際測量數據來進行驗證。所選數據集的基站數目為10個，每個基站架設有3根天線，天線參數調節范圍為：高度25～35 m，步長為5 m;下傾角0～12°，步長為2°;方向角0～350°，步長為10°。在預處理時，由于文件數量巨大，開始只讀入一部分數據，之后程序中需要用到更多新的數據時再分時讀入。三種試驗方案的收斂曲線如圖4所示：

三種算法的結果對比情況如表1所示：

表1中的實驗數據表明：改進算法一和算法二的最終結果都比標準PSO效果好。標準PSO收斂過快，得到的最優解相比算法一和算法二要差很多，這表明標準粒子群算法的直接應用不能取得良好效果。算法一的最優解從29.31%下降到24.15%，相對下降了17.06%;算法二從29.31%下降到23.70%，相對下降了19.14%，算法二比算法一改善了2.08%。

4 ? ?結束語

針對移動通信網絡中的天線參數優化問題，本文提出了改進的粒子群算法：在不同階段采取不同的搜索策略，分別以隨機初始化、大步長、小步長的方法搜索可行域內的解，能夠以較高的效率搜索到滿意解。本文算法適用于天線優化中的一類離散優化問題，并在基于實際數據的實驗中取得了較為理想的結果，能夠在較短時間內給出符合要求的天線參數調節方案，為實際的網絡覆蓋優化工作節省了成本。

同時本文還存在一些不足：在實際中的落地效果還有待進一步驗證;同粒子群算法本身一樣，對于本算法收斂性的數學證明還有待進一步的研究;如何使這種算法具有更強的普適性，也是后續工作的重點。

參考文獻：

[1] ? ?夏永康，梁曉雯. LTE網絡天線下傾角自優化算法[J]. 無線電工程， 2014（3）： 11-14.

[2] ? ?潘如君，蔣慧琳，裴氏鶯，等. LTE網絡覆蓋優化中一種基于改進粒子群的天線傾角調整的算法[J]. 東南大學學報：英文版， 2015，31（4）： 443-449.

[3] ? ? 史君黛，彭樹鐵，胡曉丹，等. 一種基于權值的TD-LTE天線覆蓋優化方法[J]. 信息通信， 2017（1）： 197-198.

[4] ? ?谷欣杏，韋再雪，李高斯，等. 基于遺傳算法的LTE系統網絡覆蓋優化方法[J]. 移動通信， 2018，42（4）： 54-59.

[5] ? ? 張捷，楊希龍. 基于模擬退火算法的移動通信網絡自規劃[J]. 計算機工程， 2017，43（5）： 83-87.

[6] ? ?KENNEDY J， EBERHART R. Particle swarm optimi-zation[C]//Proceedings of the 4th IEEE International Conference on Neural Networks. Piscataway： IEEE Service Center， 1995： 1942-1948.

[7 ] ? M CLERC. Stagnation analysis in particle swarm optimization or what happens when nothing happens[EB/OL]. [2019-03-10]. http：//clerc.maurice.free.fr/pso/.

[8] ? L DOS SANTOS COELHO， B M HERRERA. Fuzzy identification based on a chaotic particle swarm optimization approach applied to a nonlinear yo-yo motion system[J]. IEEE Transactions on Industrial Electronics， 2007，54（6）： 3234-3245.

[9] ? M RICHARDS， D VENTURA. Choosing a starting configuration for particle swarm optimization[C]// IEEE International Joint Conference on Neural Network. 2004： 2309-2312.

[10] ? ?薛明志，左秀會，鐘偉才，等. 正交微粒群算法[J]. 系統仿真學報， 2005，17（12）： 2908-2911.

[11] ? ?E F CAMPANA， G FASANO， A PINTO. Dynamic system analysis and initial particles position in particle swarm optimization[C]//IEEE Swarm Intell. Symp. 2006： 202-209.

[12] ? KENNEDY J， EBERHART R C. A discrete binary version of the particle swarm algorithm[C]//IEEE International Conference on Computational Cybernetics and Simulation. 1997： 4104-4108.