一種直下式分體液晶背光設計

董琦飛 耿向陽 周斌 張國華

（東風電驅動系統有限公司，襄陽 441001）

主題詞：直下式分體液晶 混光均勻性 混光距離 LED間距

1 前言

目前，國產汽車組合儀表大多采用液晶模組[1-5]，液晶成本較高，部分企業嘗試采用成本較低的分體式液晶方案，但由于未掌握分體液晶背光的設計方法，液晶屏仍存在顯示照度不均勻、光斑明顯的問題，不能達到預期效果。

本文設計一種用于組合儀表的直下式分體液晶，并建立一種混光均勻度計算模型，以獲得發光二極管（Light Emitting Diode，LED）矩陣最佳排列方案，從而解決分體式液晶顯示不均勻的問題。

2 混光均勻度數學模型的建立

本文設計的直下式分體液晶如圖1 所示，光線從LED 矩陣射出，經一定距離的混光，并經液晶支架和散光片多次反射后，由LED點光源形成面光源，其均勻度直接取決于混光距離H和LED間距P。

液晶屏混光均勻度測試主要采用取點測量法，常用9 點測量法，如圖2a 所示，測量選定區域的最大照度和最小照度。根據分體式液晶的測量結果（如圖2b 所示），測量區域的最大照度一般出現在LED 正上方，最小照度通常出現在相鄰4顆LED矩陣的對角線中心。

圖1 分體式液晶結構

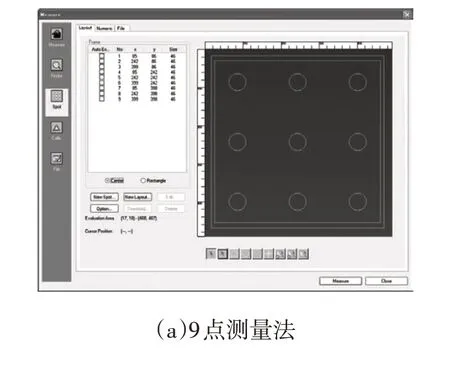
圖2 測量方法及測量結果

測量區域的均勻度U為：

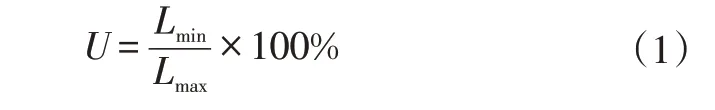
式中，Lmin、Lmax分別為測量區域的最小照度和最大照度。

根據上述測試原理，歸納均勻度的數值計算方法如下：

通常，LED 發光角度呈朗伯分布，如圖3 所示，其中，I0為LED 發光強度中的最大值，輻射光線呈余弦分布，D為光線照射面的測量點，該處光強Iθ為：

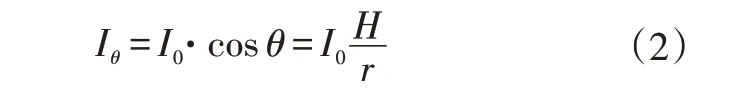
式中，θ為測量光線與中心法線的夾角；r為LED發光中心點與測量點D之間的距離。

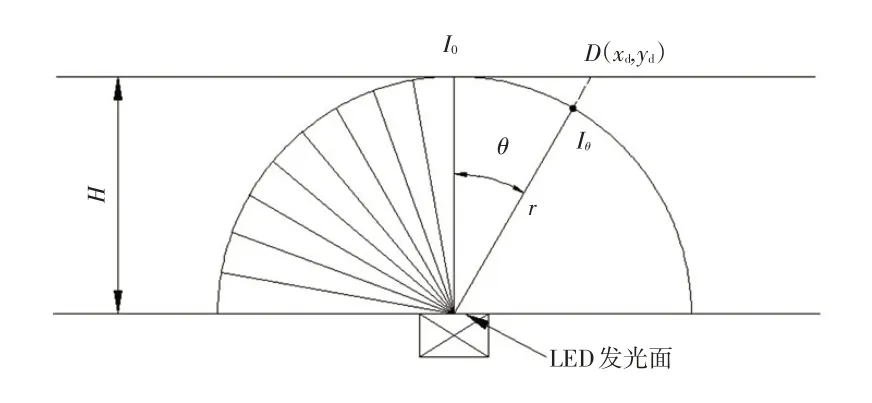
圖3 LED發光強度分布

LED 排列呈m行n列的矩陣排布，如圖4 所示。定義第i行第j列的LED 為Lij，定義L11的坐標(x1,y1)為坐標原點。X、Y方向LED 間距分別為Px、Py，則Lij的坐標為[x1+(i-1)Px,y1+(j-1)Py]，測量點D與Lij的距離rij為：

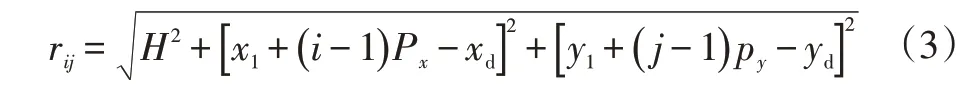
式中，xd、yd分別為測量點D的X、Y坐標。

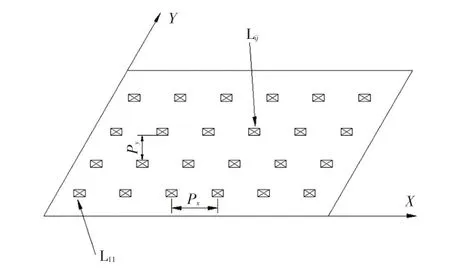
圖4 LED矩陣排布

由式（2）、式（3）可得到所有LED在測量點D處的光強I為：

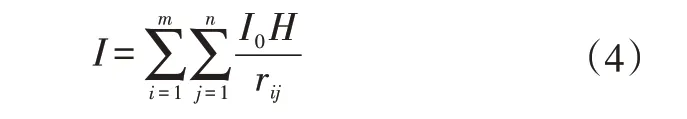
照度定義為被照射面單位立體角內的光強，則測量點D處的照度L為：

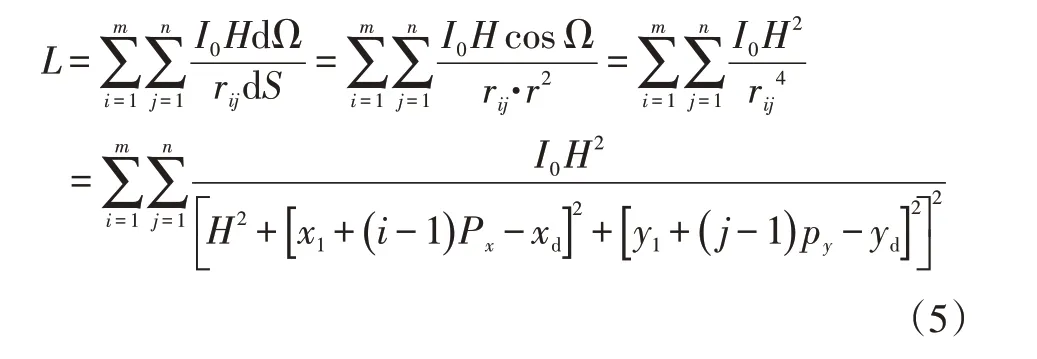
式中，dΩ為極小立體角；dS為接收點D處的極小球面面積。

由圖3可知，照射面上最大照度通常為LED中心法線方向的最大光強。當Px=Py=P時，照射面上的最大照度、最小照度通常分別按照圖5、圖6所示的方式近似計算。

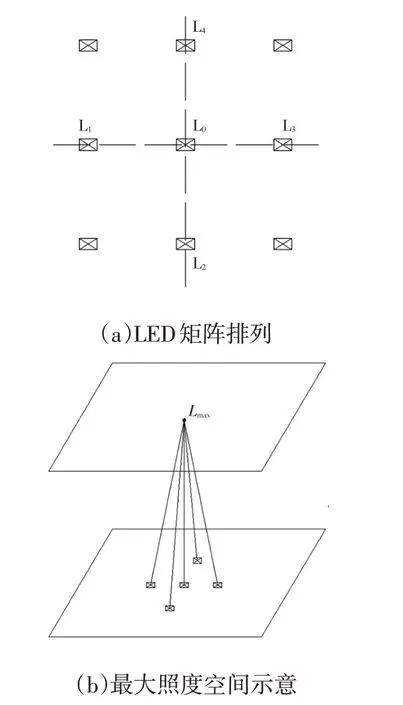
圖5 最大照度近似計算示意

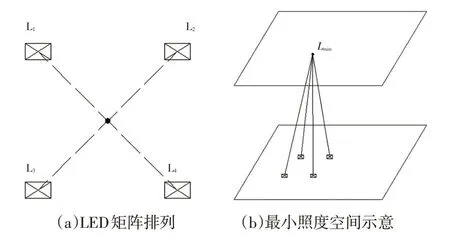
圖6 最小照度近似計算示意

當Px=Py=P時，任意行數、列數LED 矩陣照射面上的最大照度Lmax均為矩陣中的任一LED 及與之相鄰距離最近的4顆LED發光貢獻所得，見圖5。

根據式（5）近似計算可得：

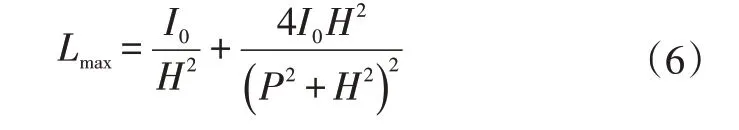
當Px=Py=P時，任意行數、列數LED 矩陣照射面上的最小照度Lmin均為矩陣中的相鄰4 顆LED（2×2 的矩陣）發光貢獻所得，如圖6所示。

根據式（5）近似計算得出：

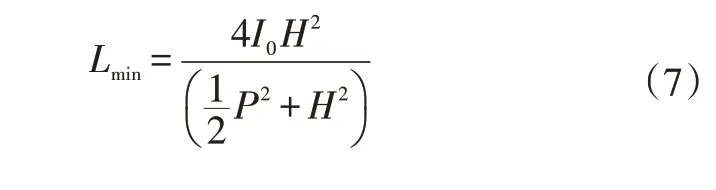
將式（6）、式（7）代入式（1）可得均勻度計算公式為：

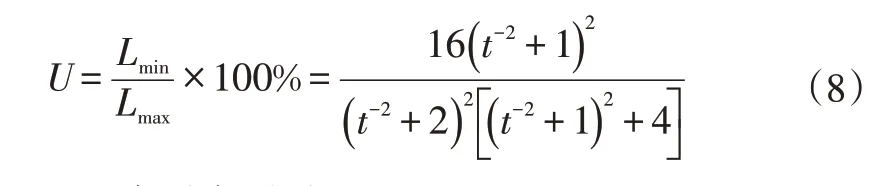
式中，t=H/P為混光因子。

由式（8）可得到均勻度U與混光因子t的關系，如圖7所示。

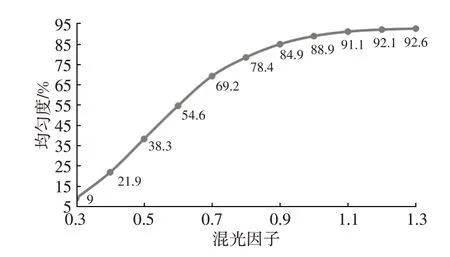
圖7 均勻度U與混光因子t的關系

3 均勻度數學模型的應用

根據式（8）計算，當U=70%時，t=0.72。由于組合儀表受支架高度的影響，混光距離H=8 mm，則P=11.1 mm。根據某液晶可視區大小（79 mm×30 mm），大致得出LED矩陣排列最多可為3行7列，即最多排列21顆LED。

考慮到實際生產中工藝等因素可能對結果有影響，故利用CAE 技術模擬分析LED 間距P=11～12 mm 時的照度均勻度，部分仿真結果如表1所示。

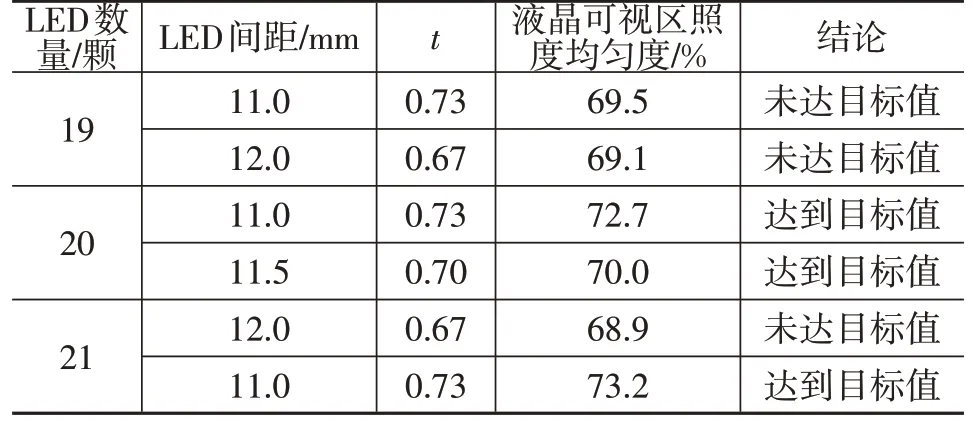
表1 仿真結果

結合數學模型計算結果與CAE 仿真結果，選定LED 數量為20 顆，LED 間距為11 mm，t=0.73 的方案為最終設計方案，仿真結果如圖8所示，并以此設計了“平底+碗狀反光面”的蜂巢結構照明系統，采用CA-2000二維色彩照度分析儀對樣件進行照度測量，實測結果如圖9所示。

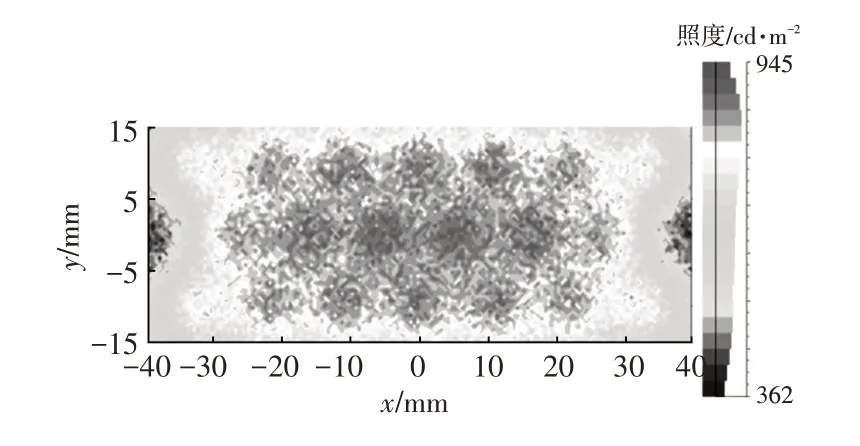
圖8 光學CAE軟件LightTools仿真結果

圖9 樣件照度實測結果

對比數學模型計算結果、CAE仿真結果以及樣件實測結果，如表2所示。

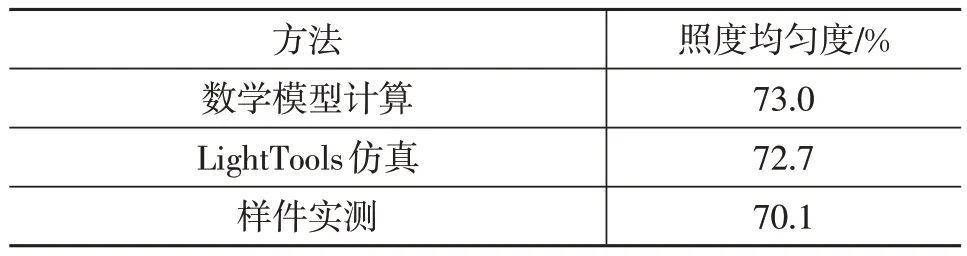
表2 結果對比

由上表分析結果可知，數學模型計算結果與樣件實測結果誤差率為4%，所以本文數學模型可以作為直下式分體液晶背光設計依據。

4 結論

a.影響直下式分體液晶照度均勻度的參數為混光距離和LED間距；

b.本文建立的混光均勻度數學模型誤差率為4%，可以作為直下式分體液晶背光設計依據。