基于交叉組合因子分析的主觀評價尺度一致性仿真研究

楊萬安 李小龍 劉紅軍

（泛亞汽車技術中心有限公司，上海 201201）

主題詞：車輛動力學 主觀評價 交叉分組因子分析 尺度一致性指標 隨機擾動

1 前言

在整車開發過程中，主觀評價常用于車輛動力學、整車NVH、座椅舒適性、外觀質量等的評價。在主觀評價過程中，評價的客觀性必須得到保證，即評價者應保持評價標準的客觀性。由于個人對被評價對象特性的偏好難以定量描述，目前沒有量化指標可較好地描述主觀評價時所依據的內在評價尺度，因此很難對評價數據進行合理篩選，進而剔除質量不高的樣本。對于主觀評價質量的研究一般分為3個方面：

a.主觀評價與客觀測量的一致性。在主觀評價的同時進行客觀測量，構造出適合的指標，使其與主觀評價的結果有較好的一致性[1-6]。

b.主觀評價團隊成員之間的一致性。團隊成員評價偏好的統一，可通過評價方法優化、嚴格評價過程、提升個人經驗等來實現。實際分析中，常使用層次分析法中的一致性檢驗及其改進方法來檢驗評價的準確性[7-8]，在樣本較多時也通過成對比較法來減少主觀誤判[9-10]，或者探索在評價結果不一致的情況下更好的決策方法[11-14]。

c.主觀評價中個人評價的一致性。目前相關研究非常缺乏，少量研究多是針對評價者的評價結果進行統計分析，試圖找到背后的影響因素[15]。

只有在個人評價尺度穩定的前提下，才能真正實現團隊成員之間的一致性。本文利用交叉分組因子分析法構造反映評價者內在尺度一致性的指標，并進行仿真分析，研究其普適性[16]。

2 評價尺度一致性指標

2.1 因子分析法與評價尺度

因子分析法的主要步驟是：假設樣本數量為m、維度為n的原始數據標準化后的數據矩陣X由公共因子F和特殊因子ε構成，即X=A×F+ε，其中A為因子載荷矩陣；利用主成分分析法對其相關系數矩陣XTX求解特征方程，可得到n個特征根λ及其特征向量β。

變量縮減過程以λ為依據，保留所有λ>1 的因子。另一種常用的依據是根據因子的累計方差貢獻率來確定適合的因子數，保留的數據方差信息>85%。

因子分析結果中的一個重要內容為因子載荷矩陣，或相應的因子載荷分布圖，它反映了各數據變量在新的因子維度中的相互影響程度。針對以往大量車輛動力學性能主觀評價數據的分析表明，第1個、第2個因子的累計方差貢獻率超過85%，其余各因子累計方差之和明顯小于前2個，因此，只用2個因子即可解釋絕大部分評價變量的方差。

根據上述初步分析，構造一個二維的因子載荷分布圖，其中X、Y軸分別為第1、第2因子載荷，每個變量（即評價指標）所對應的第1、第2因子載荷得分在圖中表現為一個點，各變量的載荷得分點（即圖中各點）之間的相對位置則反映了評價者對各變量間相互關系的主觀認知，即彼此間的夾角包含了評價尺度的重要信息，可以用來反映個人內在的評價尺度，由對各變量點間夾角αi,i+1(i＝1,2,3,…,n)變化的觀察進行量化表征。

2.2 交叉組合法及一致性指標

基于上述概念，本文提出一個可以有效觀察到個人在進行主觀評價時自身評價尺度波動的方法，即交叉組合法。首先對車輛動力學主觀評價的原始數據進行交叉重組，再分別用因子分析得到相應的因子載荷分布圖，并利用其中各變量點夾角的統計結果形成有效觀察評價尺度波動的量化指標。

對于樣本數量為m、評價項目數量為n的某評價者原始評價數據，標準化后的數據矩陣為m×n的矩陣X，交叉組合分析的具體步驟為：

a.從中依次去除1個樣本，形成交叉分組，如圖1所示。每個交叉分組數據為樣本數量為(m-1)、評價項目數量仍為n的數據子矩陣X1、X2、…、Xm。

b.針對由原始數據交叉組成的子矩陣進行因子分析，得到相應的因子載荷分布圖。

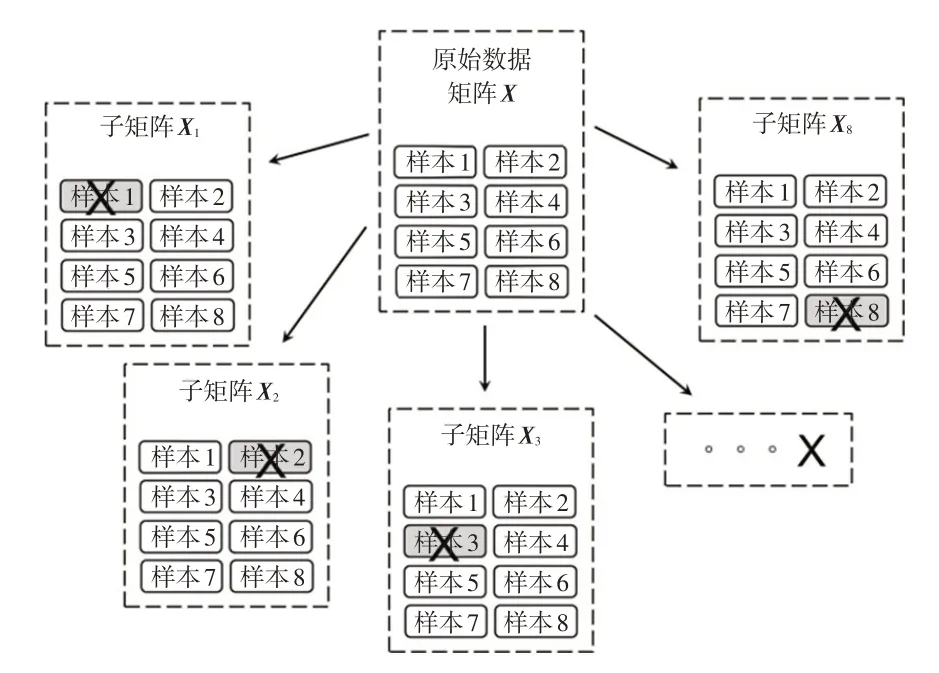
圖1 原始數據的交叉組合（以8個樣本為例）

c.構造出可以反映主觀評價尺度波動程度的尺度一致性指標（Scale Consistency Index，SCI）。

設α(i,i+1),j為第j個數據子矩陣Xj在進行因子分析后得到的第i個和第(i+1)個變量點之間的夾角，St(αi,i+1)為全部交叉分組分析中第i個和第(i+1)個變量點之間共計m個夾角的標準差。

主觀評價的尺度一致性指標可定義為：

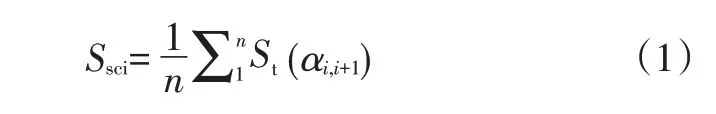
這樣，評價者的主觀評價尺度一致性由其評價數據構成的交叉分組因子分析結果體現，可反映評價者對評價變量感知尺度的量化波動。較大的尺度一致性指標反映了評價者感知尺度的波動較大，說明評價者在內、外干擾影響下的主觀評價偏差較大，可信度降低。反之，評價結果可信度較高。

3 評價尺度擾動仿真

為驗證基于交叉分組因子法的主觀評價尺度一致性指標的有效性和普適性，利用仿真過程研究多個因素對SCI的影響程度。

主觀評價的影響因子一般有多個，為簡化仿真分析的難度，以車輛動力學性能的主觀評價為研究對象，構造了由2個因子控制的數據作為研究的基準數據。

構造代表主觀評價數據標準化后的樣本數量為m、變量數量為n的矩陣X，其因子載荷矩陣為A，公共因子為F，即：

為了方便研究，構造的各變量均僅受控于2個因子F1、F2，X模擬了一位極其優秀的主觀評價者的精準評分，控制評價結果的各因子載荷不變，由其得到的相應評價尺度保持高度一致，也即對各樣本的每個變量均保持相同的評價尺度。

在真實的主觀評價活動中，評價者常因各種內在或外在影響因素產生評價尺度的波動，用相應的隨機矩陣ε、ε′代表這2種因素，最終的評價結果可表示為：

式中，ε為評價者因對某些樣本先入為主或存在偏見而產生評價尺度波動帶來的偏差，可作用于某個或多個樣本；ε′為評價者因自身技術水平或情緒波動引起的在某個或多個評價項目上的偏差。

本文從多個方面對SCI 的有效性和普適性進行仿真研究。

3.1 尺度一致性指標的統計計算

正常評價過程中，ε和ε′的變化可能導致Ssci的提高，但也可能因此使其得到改善。

為了避免其中的不確定性，采用統計方法，以大量隨機偏差擾動下尺度一致性指標計算樣本的平均值代表在該偏差擾動下相應的尺度一致性指標，而且每個模擬計算過程中均會隨機構造出新的樣本矩陣，以使統計過程更具隨機性和代表性。

隨機偏差擾動的大小根據主觀評價的實際情況確定。本文以車輛動力學主觀評價過程為例，在10分制中大部分被評價車輛的性能得分在6.5～8.5 分之間，故設定擾動范圍為±1分，在此基礎上疊加±0.25分的隨機量。

以隨機生成10 個樣本、8 個評價項目的兩因子評分矩陣為例，初步的研究表明，以將隨機擾動加載到某原始數據矩陣中的第3 個和第7 個樣本上為例進行模擬計算。當隨機規模達到1 000次以上時，尺度一致性指標的均值趨于穩定，如圖2所示。在其他樣本上進行加載也會得到類似的結論。因此，本文設定構造出的原始數據矩陣及隨機偏差擾動的次數為3 000次，確保仿真計算出的尺度一致性指標具有足夠的代表性和數據穩定性。

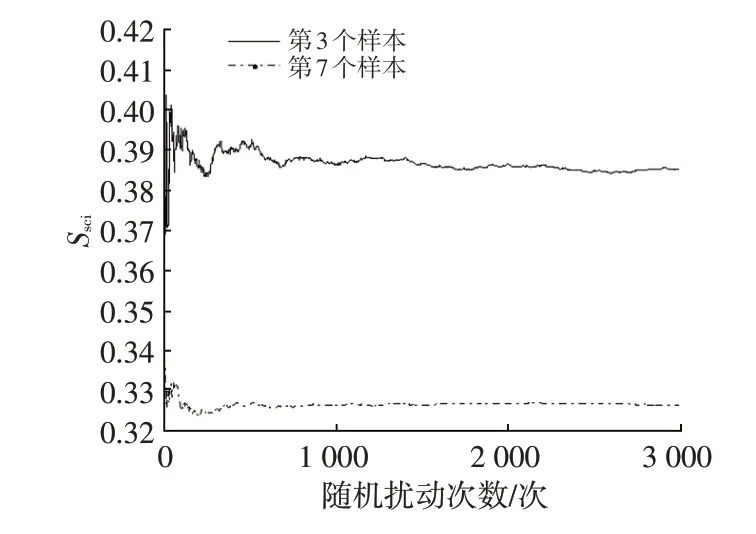
圖2 尺度一致性指標統計均值的穩定性

3.2 樣本擾動

將不同的隨機偏差擾動量加載到單一或多個樣本上，模擬評價過程中對某個或某些樣本的先入為主的個人偏好。

仿真計算結果表明：隨機擾動對加載到任意單個樣本上的擾動效果相當，且隨著擾動量級的提高明顯增加，如圖3a所示；擾動效果也會隨加載到的樣本數量明顯提高，但擾動量級的影響相對減弱，如圖3b所示。

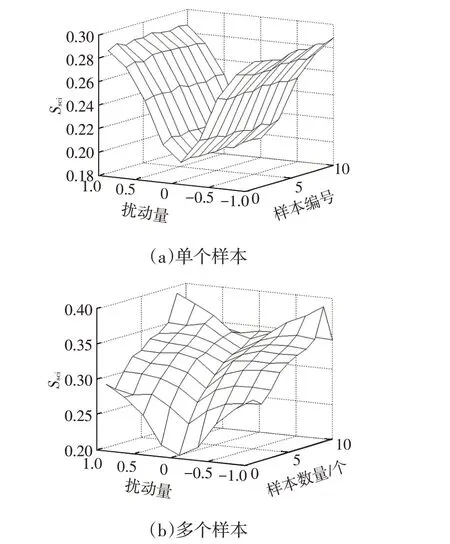
圖3 擾動加載樣本位置對尺度一致性指標的影響

3.3 樣本規模和評價項目規模

為了驗證一致性指標應用規模的普適性，根據大多數車輛動力學主觀評價活動的樣本數量和評價項目數量，將樣本規模設定為5～10個，評價項目規模設定為6～12個。

仿真計算結果表明：尺度一致性指標隨著變量規模的擴大而增加，同時在任何變量規模下，尺度一致性指標隨著擾動量級的提高而明顯增加，如圖4a所示；在任何樣本規模下，尺度一致性指標隨著擾動量級的提高而增加，但也會隨著樣本規模的擴大而明顯減小，如圖4b所示。

3.4 評價項目

對于評價者在不同評價項目上評價尺度發生變化的情況，由于因子分析前一般會進行數據的標準化，固定擾動值在進行標準化計算后會被去除，因此前文提到的用不同擾動范圍疊加隨機量的方式不再適用，改為僅用不同量級的隨機偏差進行擾動。

在相同擾動量級下，隨機擾動加載到任何一個評價項目上基本不影響尺度一致性指標的分布，如圖5a 所示，加載到多個評價項目上時，尺度一致性指標會隨之明顯增加，如圖5b所示。

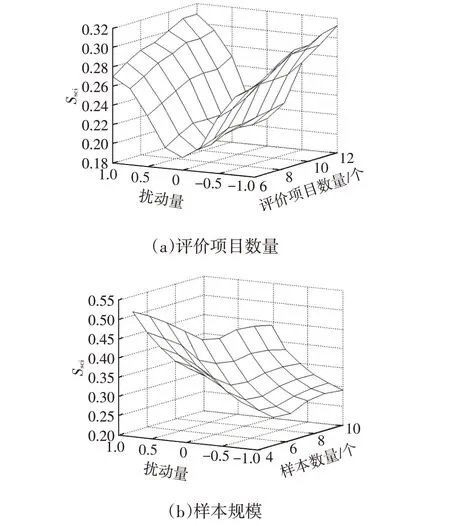
圖4 評價項目規模和樣本規模對尺度一致性指標的影響

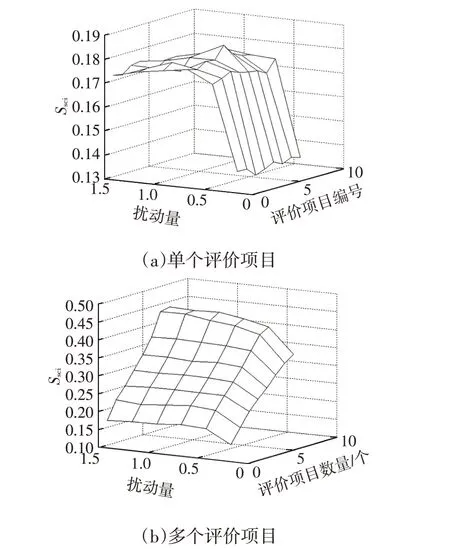
圖5 擾動加載評價項目位置對尺度一致性指標的影響

大量的仿真研究表明，只要具有相同的數據結構（即兩因子控制），尺度一致性指標均會呈現出與上述仿真類似的規律。

4 結束語

本文通過對主觀評價數據的交叉分組及因子分析，構造出可以反映主觀評價尺度一致性程度的量化指標。通過在單個或多個樣本上、不同樣本規模和評價項目規模、單項或多項評價項目上加載隨機擾動等仿真分析，驗證了尺度一致性指標的普適性和靈敏性。尺度一致性指標是關于主觀評價尺度一致性的理想衡量指標，可用于車輛動力學主觀評價過程中的評價數據質量判別，也可用于評價者精準分析評價過程中數據的量化偏差。