福州市人均收入與商品房銷售額統計分析
陳衛強
(福建師范大學福清分校電子與信息工程學院 福建 福清 350300)
引言
當前城鎮化階段,房地產行業扮演著舉足輕重的角色,一方面可以吸納成千上萬農民工就業,對全面決勝小康具有重要意義,另外一方面,可以帶動產業鏈上游產業的發展,如大型機械制造業、高端建材等,極大促進了經濟的發展。然而,大量投機性資金進入房地產炒房,導致房價虛高,遠遠超出了城鎮居民收入承受的范圍,嚴重損害了房地產行業健康發展,如何根據城鎮居民平均收入來合理確定房價值得研究。
本文以福州市城鎮居民平均收入和商品房銷售額為例,建立回歸模型,厘清之間的相關關系。由于福州市房價水平位居全國前列,依據居民收入來確定合理房價無疑具有十分重要的意義。因歷年平均房價較難獲得,通過商品房銷售額來替代房價,一般而言,平均收入越高房價就越高,商品銷售額也隨之提高,故這種替代具有合理性。借助R軟件,以福州市1978年-2018年城鎮居民平均收入建立p階自回歸模型,揭示平均收入變化規律,并預測2019年-2020年平均收入。然后利用1990年-2018年間17年的居民平均收入和商品房銷售額,建立商品房銷售額與平均收入之間線性回歸模型。并預測2019-2021年房地產銷售額。
一、模型建立


圖1 1978-2018年人均收入時序圖
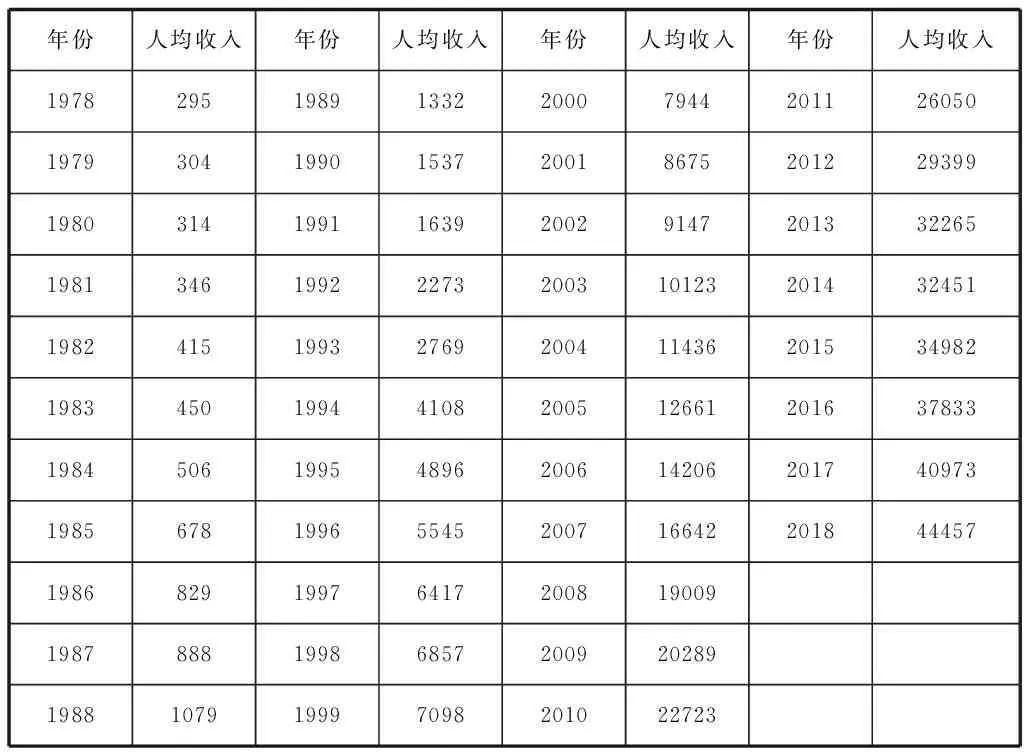
表1 福州市1978-2018年城鎮居民人均收入(單位:元)
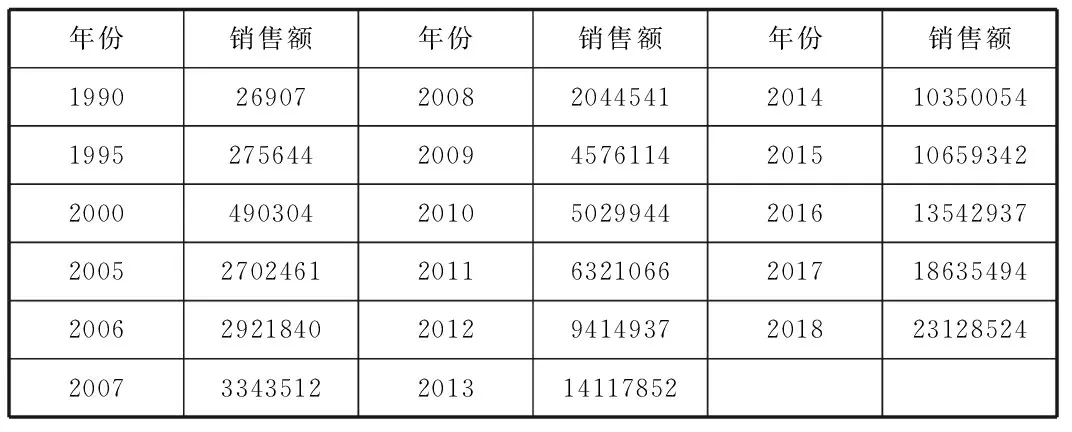
表2 福州市1990-2018年間商品房銷售額(單位:萬元)
其中x2,t=Δ2xt,εt~N(0,σ2),諸εt均獨立同分布,a0為截距項,ai,i=1,2,…,p為自回歸系數,也被稱為x2,t與x2,t-1,x2,t與x2,t-2,…,x2,t與x2,1偏自相關函數,由此可見p階自回歸模型偏自相關函數為p階截尾。p階自回歸序列的自協方差函數γ0,γ1,…,γp與自回歸系數a0,a1,…,ap之間的關系通過Yule-Walker方程刻畫:
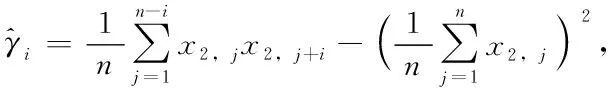
利用R軟件arma命令計算,可得p=4,四階自回歸模型的參數估計見表3,通過表3各個參數p值可知,各個參數顯著性不等與零。通過圖2下圖可知,殘差在零附近波動,表明模型擬合較好;圖3上圖是{x2,t}的自相關系數,從圖中可知,自相關協方差函數是拖尾的,下圖為殘差的自相關協方差函數,一階及其以上自相關協方差函數幾乎等于0;圖4上圖是偏自協方差函數,易見四階截尾,下圖為殘差的偏協方差函數,其在零附近波動,表明四階自回歸模型是合適的。
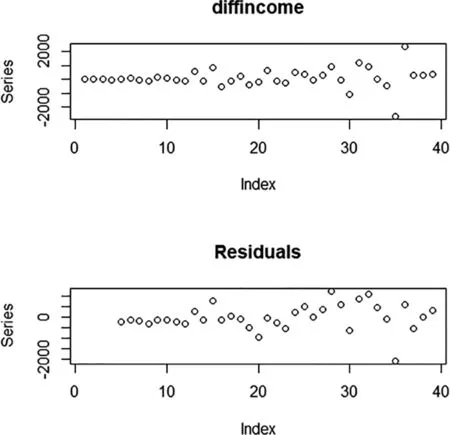
圖2 二階差分與殘差時序圖

圖3 二階差分與殘差的自相關協方差函數
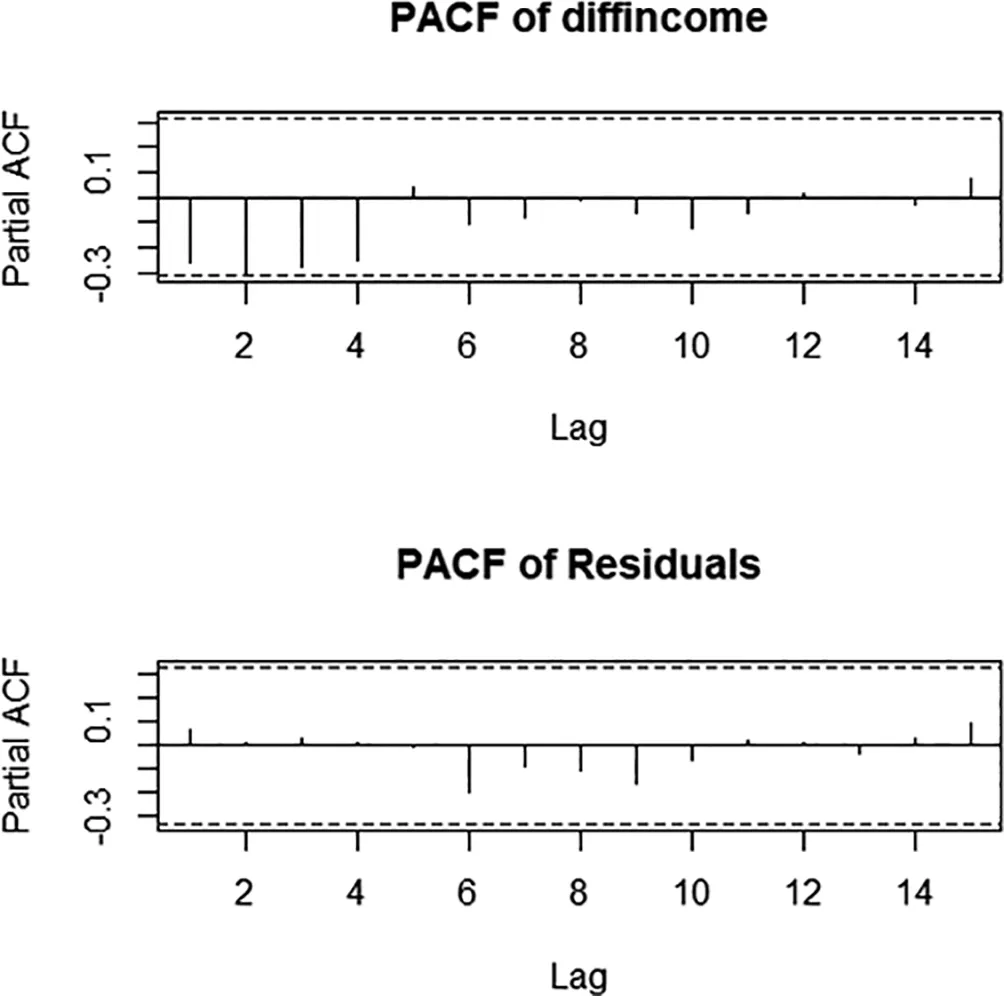
圖4 二階差分與殘差的偏自相關協方差函數

表3 AR模型參數估計
通過觀察圖5中17年人均收入和商品房銷售額的散點圖,嘗試利用線性回歸模型來建立兩者之間的聯系:yt=a+bxt+εt,其中εt獨立同分布N(0,σ2)。表4為線性回歸模型的參數估計表,經驗回歸方程為:
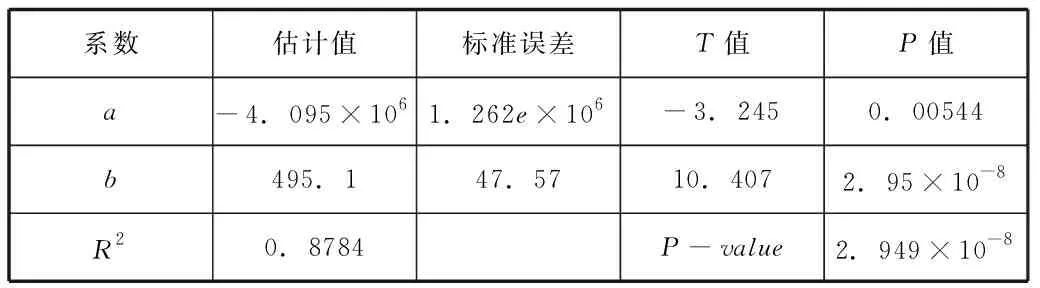
表4 線性回歸模型參數估計表
其中決定系數為R2=0.8784,線性回歸方程的p值接近于0,表明線性回歸模型通過了檢驗,回歸系數的p值均較小,說明回歸系數顯著性不等于0。從圖5中可知,利用人均收入的線性函數擬合商品房銷售額,效果較好。
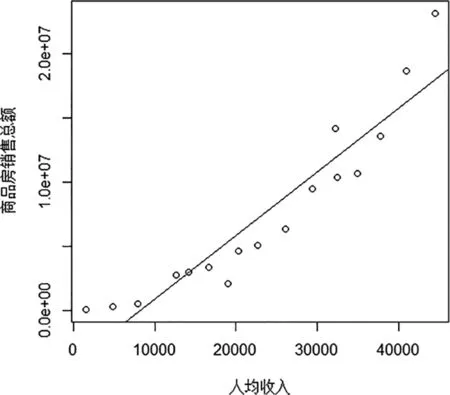
圖5 商品房銷售額與人均收入經驗直線擬合圖
二、模型預測
通過表3、表4,建立的自回歸模型和線性回歸模型分別為:
x2,t=252.16-0.6289x2,t-1-0.6780x2,t-2-0.569x2,t-3-0.6738x2,t-4+εt
yt=-4.095×106+495.1xt+εt,

而x2,t=xt+2-2xt+1+xt,當t=40時,
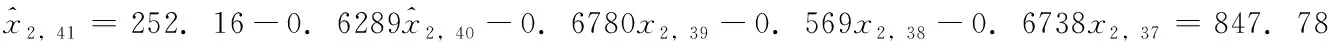

三、結語
本文利用福州市歷年人均收入數據集建立人均收入的自回歸模型,從而利用現有人均收入數據來預測未來人均收入,并通過福州市17年的人均收入和商品房銷售額數據集,建立房地產銷售額與人均收入的線性回歸模型,并預測未來三年福州市房地產銷售額,與歷史數據對比,預測結果較為合理。

