關于一元非線性回歸的一個經驗模型

謝黎東

(新疆水利水電學校 新疆烏魯木齊 830013)

對這類指數函數型回歸問題和冪函數型回歸問題，傳統方法是對其取對數，將它化成線性函數，接下來求出線性關系中的參數，然后通過逆變換求出原函數中的參數。筆者認為，在線性關系中，變量x'，Y'是否有顯著的相關性，應首先進行檢驗，只有當x'，Y'有顯著的相關性時，求出的線性回歸方程才有意義，此時求得的參數也才有意義，通過逆變換求得的原函數的參數才有實際價值。

一、基本方法

基于線性關系，關于變量x'，Y'得到一組新數據。

如果︱r︱＞r0.05（或r0.01），就稱變量x'，Y'有顯著的相關性（或高度的相關性）。

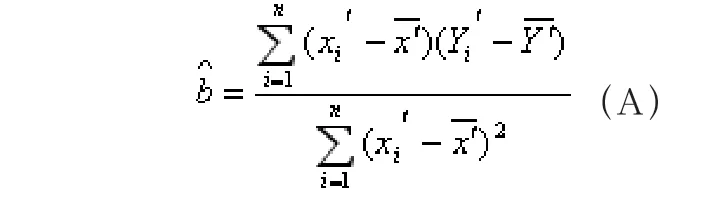
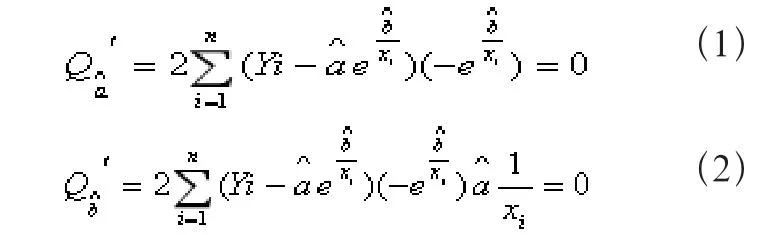
若想求出該方程組的解非常困難，缺乏操作性。

為此，將已經求出的（A）式代入（1）式就得到

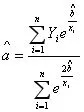
二、簡易模型

從上述基本方法，不難得出下面的經驗模型

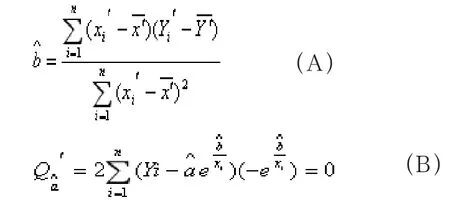
即

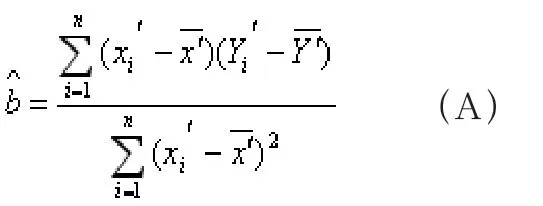
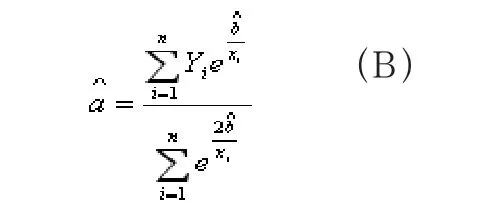
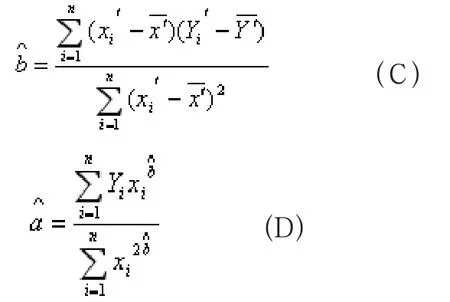
以該模型求得的回歸曲線，其擬合效果也好于傳統方法（可以驗證）。

三、實例分析

煉鋼廠出鋼時所用盛鋼水的鋼包的容積，由于鋼液和鋼渣對鋼包襯耐火材料的侵蝕，隨著使用次數的增多而增大，為了求出使用次數和增大容積之間的定量關系式，現測得此樣如下表所列，其中使用次數為，增大容積是。試求增大容積Y關于使用次數x的回歸方程。

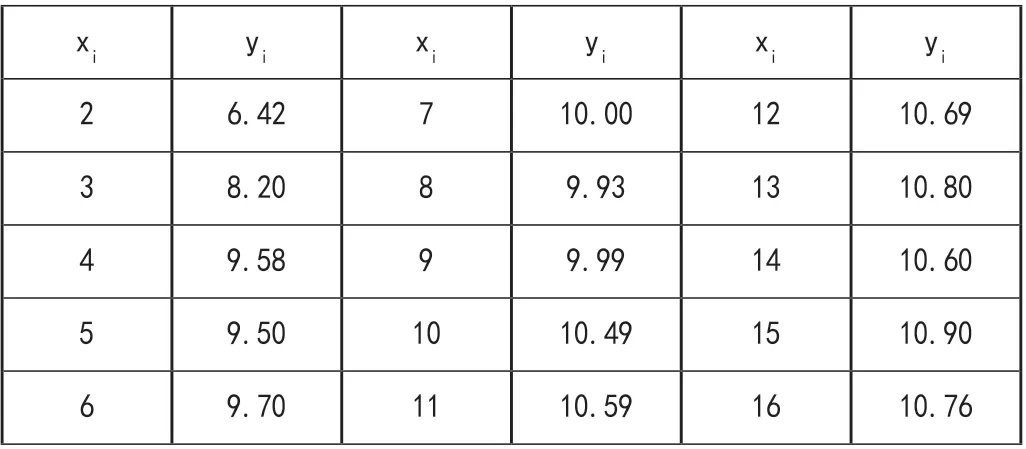
表1

解：作散點圖，在散點圖上畫一條光滑曲線，由曲線形狀看出，可能是

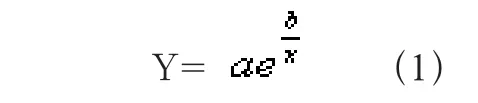
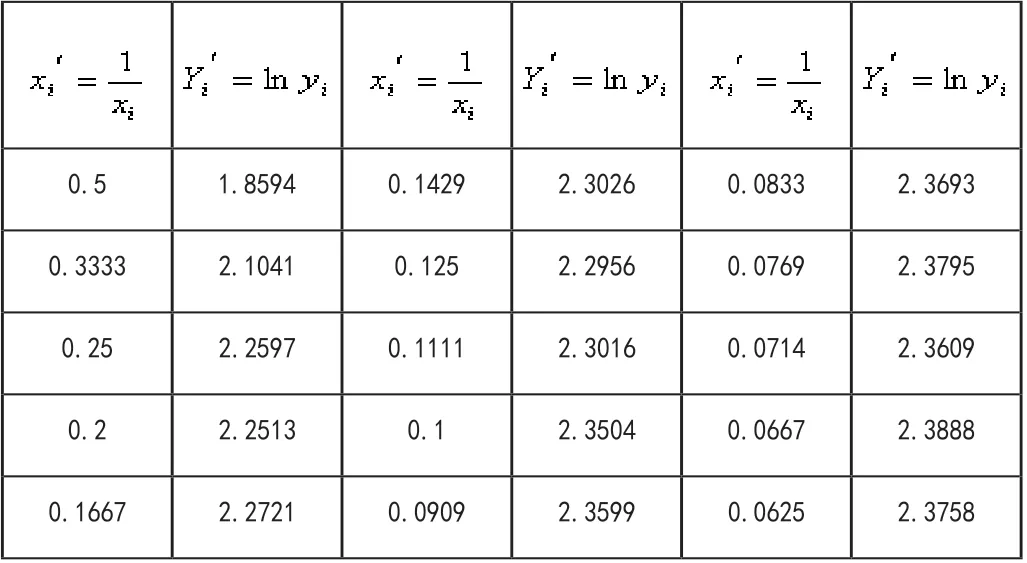
表2

按一元線性回歸計算

∑ 2.3807 34.231 0.5842 78.3844 5.2027

檢驗變量x'，Y'的線性相關性，計算

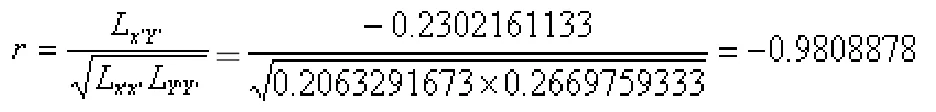
|r|＞r0.01=0.641，變量x'，Y'有高度相關性

對比看出，按本文經驗模型求出的回歸曲線，其擬合效果好于傳統方法。

四、結束語

本文所總結的經驗模型，計算方便，簡單實用，操作性強，在實際計算中對指數函數型回歸問題和冪函數型回歸問題，均可以使用本文提供的這一模型。