信息編輯：敲除健忘基因 提升學生思維能力

姚 嵐

(蘇州市新康實驗小學校，江蘇蘇州，215000)

“16+16+16=4×□”是國外一道四年級的數學競賽題，這道四則運算對我國學生而言只是小菜一碟，大多數學生都能根據等式的性質把3個16相加得到48，然后再用48除以4得到12。這個答案是對的，但出題的人并不只是為了要正確答案，他的意圖在于關注學生的數學思維。我們知道，16可以寫成4×4，于是16+16+16=4×4+4×4+4×4=4×(4+4+4)=4×12=4×□，因此，得到□=12。其實，這題考查的是乘法分配律。運用乘法分配律來解此題的思維要比運用等式性質解題的思維精致和高級得多。但在教學中，很多學生對乘法分配率的理解有不同程度的困難，更別說能熟練運用。為什么對成年人來說很容易理解的乘法分配律，對學生來說卻只有“七秒鐘記憶”呢？其實，在學習乘法分配律時，由于受多次重復練習某一類型習題的固化影響，學生常常用記憶中的模式去解答問題，把機械儲存當成信息編輯模式。一旦到了五、六年級出現小數、分數運算時，學生無法通過簡單模仿解決更高層次的問題，就會出現符號解碼流程無效的問題。所以，提高學生的信息編輯能力勢在必行。

一、建立精致型信息編輯，重構識記過程

根據信息理論，對符號的編輯技能是一種綜合技能，包括對圖形、符號、文字等各方面的理解能力、判斷能力、邏輯思維與概括能力。信息編輯的過程不是封閉地、限制地、被動地接收的過程，而是一個意義重構的過程。

例如： 25×(0.8×0.4) 25×(0.8+0.4)

=25×0.8×25×0.4 =25×0.8+0.4

=20×(25×0.4 ) =20+0.4

=20×10 =20.4

=200

從學生的解答中可以看出，他們并非簡單地抄錯符號，而是沒有把握住兩種運算律的真正意義。機械儲存讓學生識記在字母表示的乘法分配律中有括號、有三個數，而完全沒有捕捉到“乘法分配律含有二級運算，而結合律只是同級運算”這一信息，所以，學生運用自己創造的結合律和分配律混搭模式來解題，從而導致解題錯誤。

從這道題目的分析來看，學生要訓練關鍵信息的提取能力，提升大腦解碼器的信息編輯能力，讓解碼器準確無誤地將文字信息轉換成數學信息。

第一，對比訓練，識別關鍵信息。根據學生信息掃碼中經常出現的錯誤，特別是容易混淆的信息碼，教師可以對學生進行有針對性的專項對比訓練，提高學生提取關鍵信息的能力。實踐表明，對比訓練可使學生的信息編輯錯誤率明顯下降，整個信息編輯過程的有效性大大提高。

第二，仔細推敲，提煉隱藏信息。大數據時代的核心是解構信息中的一個個隱藏信息。因此，在解碼過程中仔細推敲信息源，提煉出信息源中的隱藏信息尤為重要。例如，“王師傅每天生產零件36個，李師傅每天生產零件45個，兩位師傅在今年2月共生產了多少個零件？”這一題中有一個隱藏信息需要學生仔細推敲，那就是今年2月份的天數，是平年還是閏年。

二、催生開放性信息編輯，加深理解運用

數學信息需要依靠各種信息來呈現，一般來說，有文字信息、符號信息、圖像信息，等等。文字信息是在語言信息的基礎上形成和發展起來的，是儲存、傳遞和加工信息的工具。文字信息雖通俗易懂，但有時表達過于繁瑣；符號信息雖簡潔嚴謹，但過于抽象；圖像信息雖形象，但未必全面。學生的識別能力不同，光靠解碼器的精致性信息編輯還不足以加深理解，因此，優化信息編輯方法，實現開放性信息編輯顯得非常重要。教師可通過開放性信息編輯，發揮各種信息的優勢，活化學生的思維，加深學生對信息的理解，為信息解碼提供保障。

第一，文字信息編輯為圖像信息。當信息源發送的文字信息較為抽象，而解碼器對符號的抽象性把握不準時，圖像信息的出現無疑是一場及時雨。文字信息轉換為圖像信息，不僅可以清晰解碼思路，而且為解碼器實現數形結合提供能力保障。仍以“16+16+16=4×□”這道競賽題為例，16+16+16=4×4+4×4+4×4其實代表著三個邊長為4的正方形相加，最后可以拼成一個4×(4+4+4)=4×12的長方形，如圖1。教師把抽象的文字信息編輯成圖像信息中的矩形，并對其進行分割和拼接，讓學生更容易理解和運用乘法分配律。

圖1 文字信息編輯為圖像信息示例

第二，文字信息編輯為符號信息。文字信息轉換成符號信息是有效轉換信息中的一種方式。如果能夠選取適當的符號重新敘述問題，學生就能更清晰地審題和探索解題思路。

三、激發再生性信息編輯，實現升華創造

學習數學最重要的是學習數學思想和思維方式。如果說從限制性信息編輯到精致性信息編輯是一種完善，從精致型信息編輯到開放性信息編輯是一種進步，那么，從開放性信息編輯走向再生性信息編輯就是一種升華。學生接收到符號源后能通過觀察發現、歸納類比、空間想象、抽象概括、反思構成、演繹證明等再生性信息編輯舉一反三地解決更高層次的問題，有利于構建從識記、理解到創造的思維新方式。

在開放性信息編輯中，將抽象的文字信息編輯成圖像信息并不是終點，而是思維升華的前奏。如這一具有挑戰性的問題：“1×1×1+2×2×2+3×3×3+4×4×4=？”通過計算，學生很快就能得到答案100。但正確的僅限于答案，而不是數學思維。如果題目改為“1×1×1+2×2×2+3×3×3+…+1000×1000×1000=？”，通過純粹的計算很難再順利得出答案，學生就無從下手。這時，學生如果能巧用形象思維進行再生性信息編輯，問題就能迎刃而解，還能取得舉一反三的效果。

如圖2，兩個數相乘可以理解為矩形的面積，那么三個數相乘就可以做以下嘗試：把1×1×1看成1個12，把2×2×2看成2個22，把3×3×3看成3個32，以此類推，把n×n×n看成n個n2，拼起來就可以得到如圖2所示的金字塔。

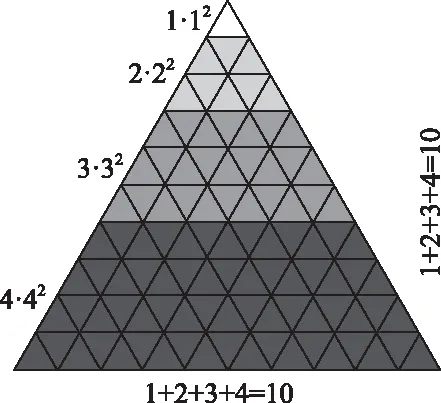
圖2 文字信息編輯為圖像信息示例2

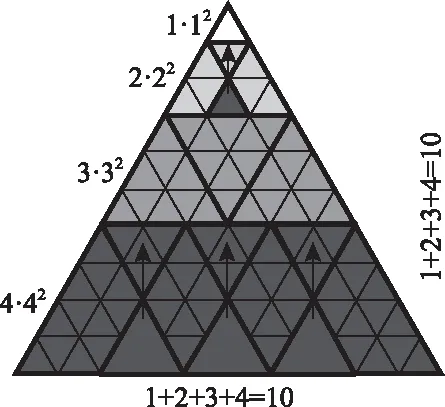
圖3 文字信息編輯為圖像信息示例3

通過編輯就可以知道，從1開始的連續奇數相加，其和為項數的平方。所以，圖2的金字塔就可以編輯得更直觀一些，如圖3。

通過幾次再生性編輯的直觀證明，學生推導出1×1×1+2×2×2+3×3×3+…+n×n×n=(1+2+3+…+n)2，即從1開始的連續立方數求和，最后變成一個完全平方數，1×1×1+2×2×2+3×3×3+…+1000×1000×1000不通過計算也能迎刃而解。因此，激發再生性信息編輯，實現升華創造，對培養學生的數學思維具有重要作用。