雙參卷積理論模型預測交通通行時間

金楠森，劉美玲 ，2，谷欣然，韓雨彤

1.東北林業大學 信息與計算機工程學院，哈爾濱 150040

2.哈爾濱工程大學 計算機科學與技術學院，哈爾濱 150001

1 引言

智慧交通是以大數據、云計算、衛星導航等新興IT技術產業為基礎，具有更方便公眾出行的，優化的交通運輸管理體系，通過數據的積累和傳遞，更好地開發和利用數據的一種綠色、便捷、安全、暢通的交通模式。

隨著城市經濟的發展和人們生活節奏的加快，我國整體道路運輸的高速發展，機動車增速過快，交通擁堵已經成為“不治之癥”，如何緩解交通擁堵問題迫在眉睫。人們無法掌握出行路段的實際情況，不能合理地選擇出行方式和安排出行時間，導致某時間段內人車流密度膨脹，是造成交通擁堵的一大成因，要想解決擁堵問題，首先要對活動人口和車流進行有效處理。此時，能夠對行駛路線進行有效的時間預估就顯得尤為重要。

時間預測看重的主要是精確度和實效性，現有的一些傳統方法存在一定的缺陷，如對車輛進行時間預測時，通常利用的都是歷史通行時間數據或假設情況來建立算法；忽略車輛的運行狀態以及道路在某時刻的真實情況。

國外在二十世紀五六十年代，開始在城市周邊布設檢測裝置，收集道路信息，20世紀90年代開始對浮動車系統有了一定的研究。我國從2000 年開始，由于浮動車數據日趨增加，對浮動車系統的一系列研究也已經成為熱點問題。有效地預估車輛的通行時間對交通出行有極大的好處，目前對時間預測的研究常用的有以下方法：

基于歷史數據的預測模型。Smith 等人[1]提出了基于歷史數據的預測模型用來預測車輛的到達時間，主要是使用大量的歷史數據，并假設交通模式為循環變化，以車輛的第一次達到時間為基礎在固定位置進行測算；Lin 等[2]主要是根據真實到達時間和公交汽車提供的時刻表之間的誤差校對，針對郊區出行者，對公共汽車的到站時間進行實時預測；涂麗佳[3]利用歷史數據建立后綴索引樹的存儲結構，根據歷史數據提供的通行時間的結果，在該種存儲結構下可以快速地獲取子路徑序列和相應的軌跡通行時間。

變量衰減預測模型。Chien等人[4]通過大量由獨立變量構成的函數建立多變量模型，估算出非獨立變量的值，即根據車輛的始終點的距離、時間差、中途滯留的時間等變量作為獨立變量，由衰減模型的原理，建立預測模型。

基于人工神經網絡的預測模型。常見的神經網絡有BP、RBF、AML等多種類型。早有研究證明了利用神經網絡得到的結果與其他的預測算法相比準確度更高。基于人工神經網絡的預測模型需要經歷訓練和預測兩個階段，在訓練階段的有監督學習模式下，神經網絡重調連接在每層的權值來獲取理想的輸出期望。Lin和Yang 等人[5]針對于不同時間窗口下的車輛運行特征和交叉路口信號燈對車輛的影響建立了兩層的神經網絡進行研究；蔣渭忠等人[6]建立3 層BP 神經網絡模型，利用MATLAB軟件確定隱含層神經元數目為9個，并利用預測樣本驗證了模型的可行性，得到誤差在10%之內的結果。

Kalman濾波模型。Kalman濾波模型屬于一種優化的自回歸算法，因為其高效率、用途廣等特點已經被廣泛應用了幾十年。Wall 等人[7]利用Kalman 濾波對西雅圖市的車輛進行追蹤記錄，結合歷史數據和實時數據，通過統計學的知識預測時間，獲得時間分布狀態。

基于隱馬爾可夫模型的預測模型。歐陽黜霏[8]用非參估計方法將隱馬爾可夫模型擴展為無限狀態模型能夠對實時的數據進行在線預測。

基于支持向量機的預測模型。主要用來解決非線性的問題，避免了人工神經網絡里的結構問題。Yu 和Yang[9]利用支持向量機，結合了天氣、時間等5個因素，用前車的行駛速度預測之后路段上車輛的行程時間。

除了以上方法，唐俊[10]還利用地圖匹配技術，提出經驗模態分解與SVR結合的時間預測方法；朱國華[11]將數據分為靜態行程時間數據、歷史監測數據和無檢測器路段數據，劃分時間間隔，并給第t個時間間隔設施權值計算行程時間；李勍等人[12]用K臨近法結合歷史數據預測時間，并用時間協方差對預測的時間進行校準；邢雪等人[13]則引入預測強度并基于預測強度進行聚類預測時間；以及部分針對公共汽車進行預測時間的方法。

近些年來對時間預測有了更深參層次的研究，曹天揚和申莉[14]以路阻函數為基礎，提取了流量和車速與路段行駛時間之間的數學關系，建立了適用于最小二乘法求解的預測函數；尹紀軍、王棟梁等人[15]通過采樣周期計算量歷史旅行時間值、實際旅行時間值與平滑系數的關系，確定了短期旅行時間的預測值，呂路[16]從事件狀態下交通流統計特性出發，建立了波動理論-BP神經網絡事件狀態下快速路行程時間預測組合模型計算行程時間。

現有的研究在智慧交通預測時間[17]方向已經取得了一定的成果，但是由于非傳感器記錄的車輛信息中變量較少及它的不確定性等因素，預測通行時間的研究方法并不能很好地得到所需要的結果。本文考慮到車輛特征狀態這一影響因素，并結合車輛行駛速度構建雙參卷積速度理論模型，利用分割軌跡后車輛的加速度計算通過時間，為城市居民出行安排提供了合理的理論依據。

2 基于密度劃分的雙參卷積理論模型分析與研究

2.1 模型成立分析

（1）數據預處理：對數據集中重復、不穩定等數據進行篩選清洗，定義數據抽樣規則并將數據集分為訓練集和測試集兩部分。

（2）模型建立前參數準備。路段中各車輛相鄰軌跡點間的距離和行駛速度是建立實驗模型、預測結果的必要條件，通過分析建立公式來計算待測變量。

（3）速度突變值處理：由于對待測變量的研究使結果中出現異常的突變值，通過箱線圖結合R語言對數據結果進行范圍規劃，去除異常突變值。

（4）基于皮爾遜的載客相關性研究：利用皮爾遜相關系數研究車輛載客情況和行駛速度之間的相關性，根據結果特征建立速度模型。

（5）基于密度劃分的雙參卷積理論模型：結合車輛載客情況和行駛速度，調整設置合適的卷積模板，建立雙層卷積理論速度模型。

（6）設置修正因子：因為只使用雙參卷積理論模型得到的結果有一定的誤差，所以設置特征修正因子，提高實驗結果的精確度。

（7）預測通行時間：將實驗長路段進行軌跡分割，使用雙參卷積理論模型得到相應的理論均值速度，利用速度-加速度模型預測車輛的初始通行時間，最后使用修正因子進行修正得到最終的道路通行時間。

2.2 雙參卷積速度理論模型的分析建立

2.2.1 數據預處理

本文使用的是成都市1.4萬輛出租車，將近14億條的GPS軌跡數據，數據中包含有出租車ID，經度，緯度，載客狀態（0 表示無載客，1 表示載客），時間這5 個參數。清洗掉其中重復和異常的記錄，忽略了00：00：00—05：59：59這一時間窗口內的數據。本文中，實現的是預測某路段的通行時間，為了更有利于實驗的進行，定義了如下實驗道路的抽樣規則：

（1）不選取含有異常車速（如時速極高或突變）的路段；

（2）在實驗路段的起點和終點，保證車輛不會有停留時間。

將所有的數據集分為訓練集和測試集兩部分。對實驗數據做如下基礎定義：

（1）假設車長對車輛速度的計算沒有影響；

（2）司機的駕駛行為均良好，沒有交通異常事件發生；

（3）不考慮天氣因素和車輛自身狀態因素以及乘客在上下車時的停留時間。

2.2.2 基礎均值速度

本部分主要介紹建模準備階段的參數的求解過程。

根據數據中的已知變量，即軌跡點的經緯度，使用坐標轉換法把經緯度投影到二維坐標系中。由于數據集的數據記錄間隔是1 s，所以兩個連續軌跡點之間的距離可以認為是直線距離。最后結合歐式距離計算公式計算得到某一路段上同一車輛每兩個相鄰軌跡點間的車輛距離。

將訓練集和測試集一同使用上述坐標轉換法進行處理，并將處理后的訓練集數據進行篩選，得到實驗路段的各車輛數據設為矩陣P：

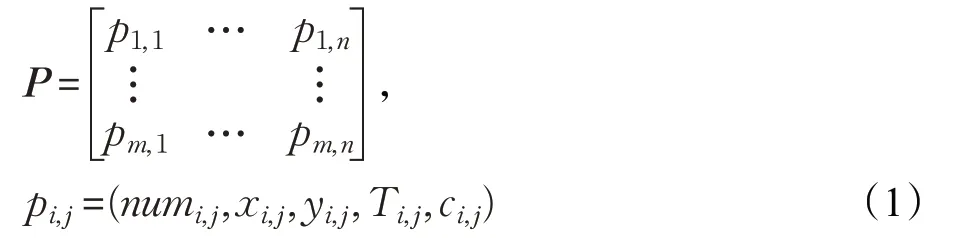
其中，m代表著路段有m輛車，實驗路段各車輛軌跡點最多的軌跡點個數記為n。角標i,j代表的是這一路段第i輛車的第j個記錄，即第i輛車的第j個軌跡點。Numi,j代表的是第i輛車的序號，xi,j代表的是投影后的x坐標，yi,j代表的是投影后的y坐標，Ti,j代表的是記錄時間，ci,j代表的是該車輛的載客狀態。

計算前一個軌跡點和后一個軌跡點之間的距離和時間Li,j和Ti,j：

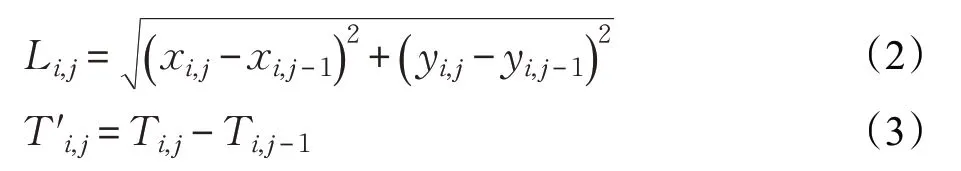
本文利用大量數據驗證得出較好的時間間隔，規定：

根據相鄰的兩個軌跡點間的相關數據，由公式（5）計算基礎均值速度為：

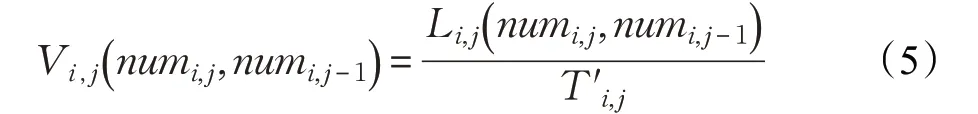
實驗得到的基礎均值速度Vi,j可構成速度數據集。

2.2.3 速度突變值處理

在上述實驗設計中，為了計算簡便，將車輛數據集中，因此必然出現相鄰的兩個軌跡點分屬于不同的車輛，即前一輛車的最后一個軌跡點數據和后一輛車的第一個軌跡點數據被作為同一輛車的數據處理計算，此類情況計算得到的基礎均值速度會出現異常（速度突變），為了消除該種情況對實驗結果的影響，通過箱線圖來輔助去除速度數據集中的異常速度。

將邊界值定義為Di，其對應位置定義為Wi,N代表的是數據集序列中包含的項數。

（1）定義下四分位數、中位數、上四分位數分別為D1、D2、D3，它們所對應位置的數值分別為W1、W2、W3。

①邊界值對應位置：

②邊界值的數值：

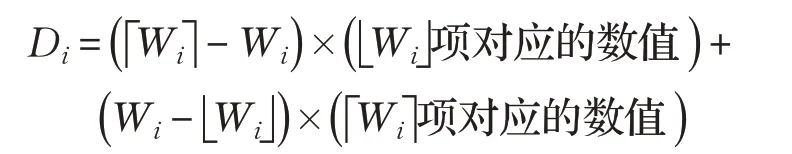
（2）將上限和下限以及四分位數分別定義為D4、D5、W。

①四分位距W：

②上限D4：

③下限D5：

由以上限界值構建箱線圖去除異常值。

2.2.4 皮爾遜系數分析研究載客相關性

皮爾遜相關系數r描述的是兩個變量間相關性強弱的程度，r的絕對值越大，表明相關性越強。

通常情況下通過表1 中相關系數取值范圍判斷變量的相關強度。

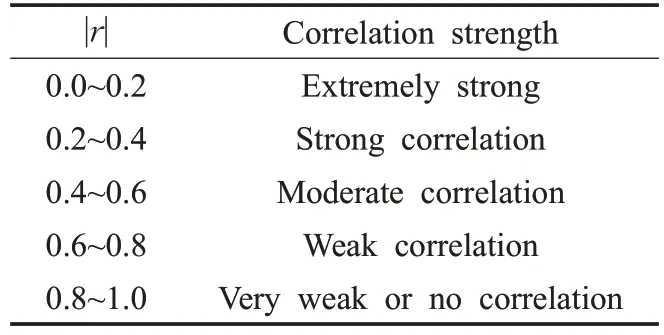
表1 皮爾遜相關系數

為了充分利用車輛的部分特征狀態，本文實驗選擇將車輛的載客情況作為影響因素之一，判斷載客情況與基礎均值速度之間是否有相關性。

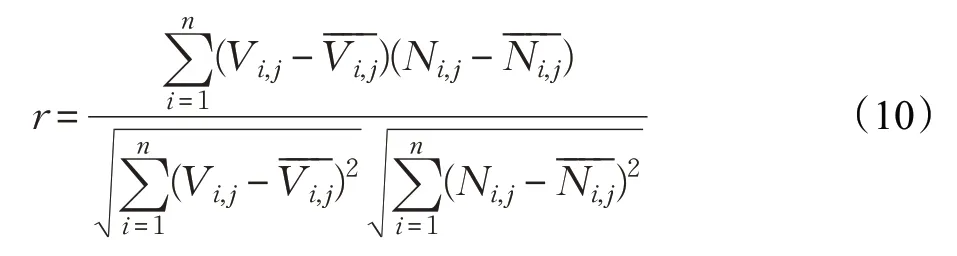
其中，r表示所求的兩個變量之間的相關系數，n表示軌跡點數，Vi,j表示速度數據集中的基礎均值速度值，表示數據集中所有速度的平均值；Ni,j表示載客情況，值為0或1，表示載客情況值的平均值。

2.2.5 雙參卷積理論模型

實驗證明速度與載客情況之間的相關性存在，則利用這兩個參量來建立以下的雙參卷積理論模型。建模結果定義為理論均值速度，分別為載客時的理論均值速度v1和不載客時的理論均值速度v2。

（1）將速度數據集中的基礎均值速度分為載客和不載客兩種情況，分別設置為載客速度矩陣z1和不載客速度矩陣z2。實驗路段中每個車輛都有一個z1和z2。

z矩陣中的元素都是車輛速度，根據相應車輛載客與否的軌跡點數來確定相應的矩陣大小n1、n2，比如實驗路段中第i號車擁有15 個載客的軌跡點數，擁有25個不載客的軌跡點數，那么相應的n1、n2為4 和5，矩陣元素空缺用均值來填補。

（2）設置動態自適應3×3的卷積核模板A：

以載客速度矩陣z1為例進行卷積運算，假設n1=5，則可以形成9個3×3的矩陣序列X：

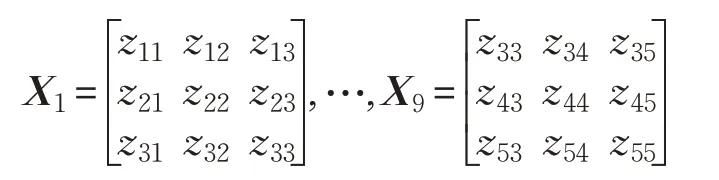
對9個矩陣序列X分別進行中值濾波運算，每個矩陣得到一個輸出值Pa(a=1,2,…,9)，則A矩陣中的值為：

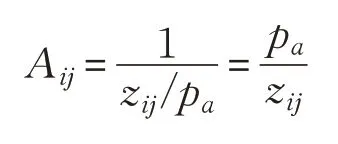
最終計算得到9 個3×3 的卷積模板A，分別對應著9 個矩陣序列X。

（3）依次使用9個卷積模板A與和其對應的矩陣序列X，進行9 次計算，設每次計算得到的結果為x，最后得到 9 個x的值。

（4）9個x最終構成一個新的3×3的矩陣X*，這樣就達到了降維的效果，并設置新的卷積核模板A：

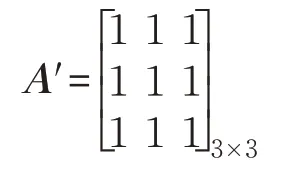
用X*矩陣和卷積核模板A進行卷積運算，得到某一輛車的載客理論均值速度v1。

（5）對于不載客速度矩陣z2，假設n2=5，同理計算得到對應車輛的不載客理論均值速度v2。

（6）最后對于實驗路段所有車輛的z1和z2求平均得到各路段最終的載客理論均值速度和不載客理論均值速度。

2.2.6 實驗路段時間預測

實驗將所選實驗路段進行軌跡分割，分為上、中、下游三段，并分別對三段道路上的車輛進行速度計算，得到載客時的理論均值速度VZ1、VZ2、VZ3 和不載客時的速度VnZ1、VnZ2、VnZ3。利用理論均值速度結合加速度計算得到通行時間。

2.2.7 設置修正因子

經過測試集測試，實驗使用雙參卷積模型計算得到的時間與車輛通行的真實時間之間存在一定誤差，為了使預估結果更接近真實情況，本文通過定義修正因子來提高精度，減小誤差。

由于實驗道路長度為1.4 km，每輛車的行駛軌跡始末點的距離都不一樣，因此按照行駛軌跡始末點的距離，分為14種不同情況。例如，當某輛車的軌跡始末點的距離在0～100 m 之間時，將這輛車劃到第一種情況；當某輛車的軌跡始末點的距離在100～200 m之間時，將這輛車劃到第二種情況；當某輛車的軌跡始末點的距離在1 300～1 400 m之間時，將這輛車劃到最后一種情況，且每種情況里包含的相關數據構成一個數據集，并根據修正因子分別對由每個數據集算出來的時間進行修正。

在針對整段長為1.4 km的路段時，某輛車通過的時間T使用對應的修正因子Flag修正。

修正后時間T′：

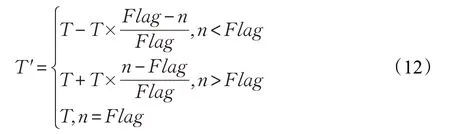
n為這輛車通過這段路時被記錄的軌跡點的個數。

對最終結果評價指標，采用絕對百分比精度公式計算結果精確度：

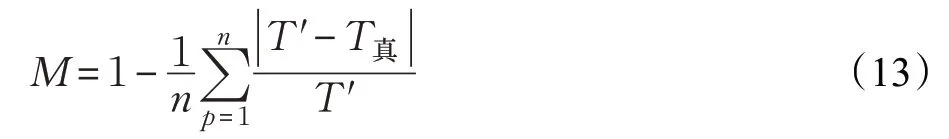
M代表百分比精確度，n代表實驗路段的車輛數，T代表實驗經過雙參卷積模型和修正因子處理后得到的最終預測時間，T真代表測試集中兩軌跡點間的真實時間。M的值越大代表精度越高，結果更加接近測試集里的真實時間。

3 實驗結果分析

3.1 速度異常調整

圖1 為箱線圖的結果，縱坐標代表速度值，由圖可以明顯看出，箱線圖的上下限控制在0～80 km/h，因此將速度值大于80 km/h的定義為異常值并去除。

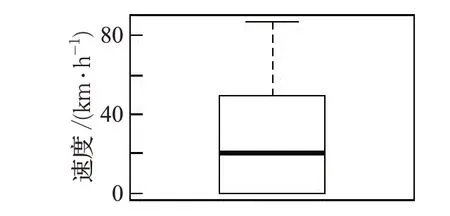
圖1 實驗路段速度值的箱線圖結果分析

3.2 路段處理及分割依據

本文實驗在特定時間窗口內的實驗路段的GPS 軌跡點投影如圖2所示。

由圖2 可以看出在選定道路上，車輛密度較大，車輛軌跡點分布密集且均勻，因此將此路段按照上、中、下游進行軌跡分割。保證路段上的軌跡點數目被平均分配，即三段路包含的軌跡點數目相同。

3.3 皮爾遜系數分析研究載客相關性

車輛行駛速度與載客情況的相關性分析如表2所示。

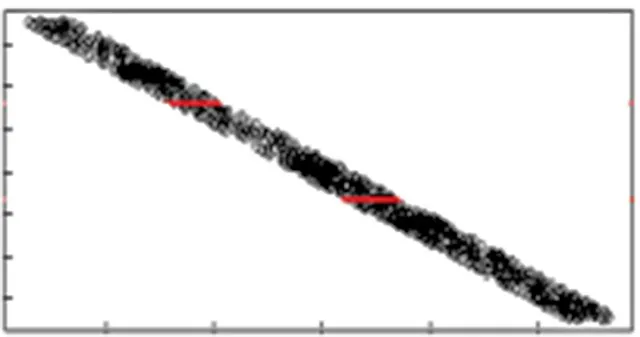
圖2 實驗路段的車流密度投影及子路段劃分

第一列為車輛編號，第二列為兩個變量，分別是速度(speed)和載客情況(cp)。每輛車速度變量后對應的5個數值為不同載客情況下的速度值，而載客變量后對應的5 個數值表示的是車輛是否載客（0 表示不載客，1表示載客）。最后一列數據r表示的是相關系數。

由車輛行駛速度與載客情況之間的相關性，分析得到以下結論：

當r＞0 時，表示載客(cp=1)的平均速度比不載客(cp=0)時的平均速度大，且r絕對值越大，相差越明顯。

當r＜0 時，表示不載客(cp=0)的平均速度比載客(cp=1)時的平均速度大，且r絕對值越大，相差越明顯。

當載客情況一致時，即選取的車輛的5 組值均為0或1時，r的值為0。

3.4 模型建立及結果實現

利用基于密度劃分的雙參卷積理論模型算出的速度結果如圖3所示。

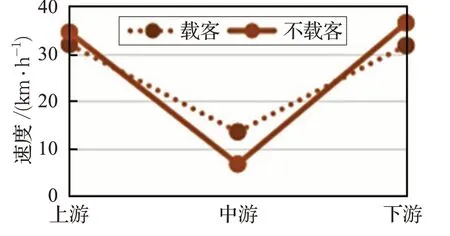
圖3 不同載客情況下實驗路段的速度結果顯示

對實驗路段進行中心點標記，如圖4所示。

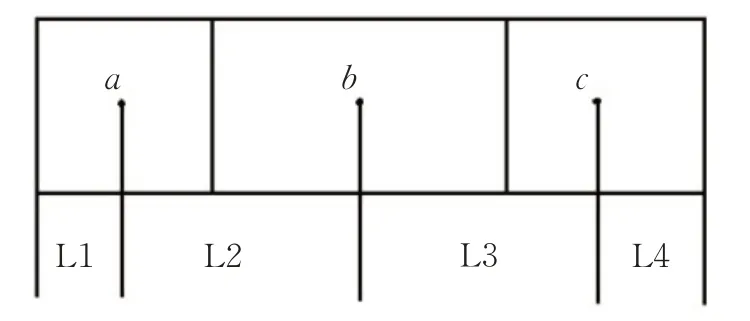
圖4 預測道路劃分情況顯示

令路段中心點a、b、c的速度為已知的載客（不載客）理論均值速度VZ1、VZ2、VZ3(VnZ1、VnZ2、VnZ3)，根據車輛行駛的情況，計算每段路的加速度并計算通行時間。

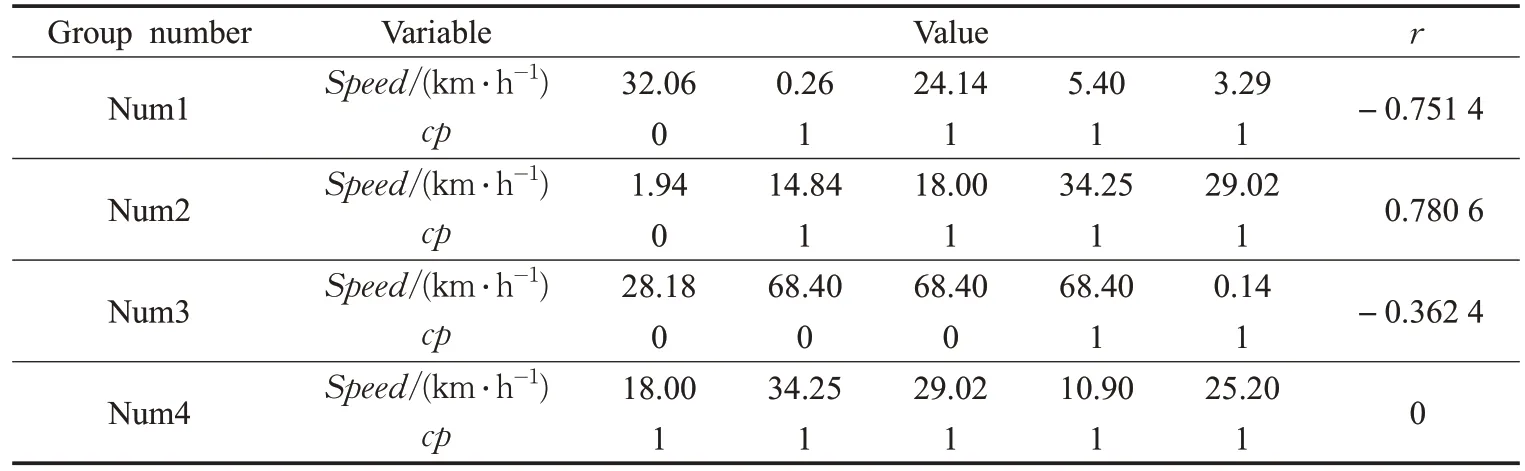
表2 速度與載客情況的相關性分析結果

在 L1 與 L4 路段車輛為勻速行駛，L2 與 L3 路段車輛進行相應的加速或減速行駛。因為實驗數據沒有恰好處于兩端的車輛軌跡數據，所以根據各車輛起點和終點所在位置使用相應的速度和加速度進行計算，再經過相應的修正因子進行修正得到該車輛從起點到終點所用的通行時間。

3.5 修正因子修正誤差

采用絕對百分比精度公式計算可知，①結果的精度在60%左右，但改進后的方法②結合修正因子后得到結果的精確度如圖5所示，實驗預估的車輛通過某段路的時間與真實時間之間達到了90%左右，精度得到了有效的提高，充分證明本文實驗的方法有較高的準確性、可用性和真實性，較準確地接近車輛真實的通過時間。

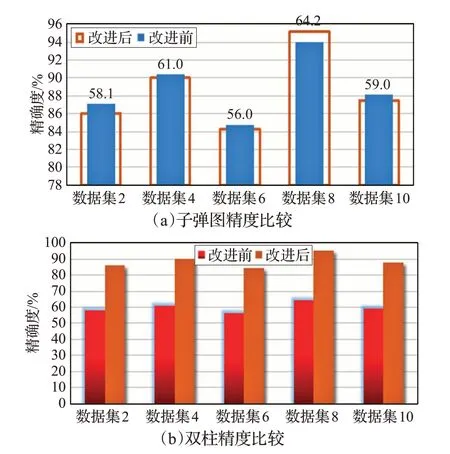
圖5 改進前后時間精確度結果對比

4 總結及展望

本文根據原始數據集中僅有的車輛經緯度和點時間數據，建立算法得到必需參量軌跡點間距和車輛行駛速度。基于傳統的時間預測研究方法的不足，融入了新的車輛的運行特征：載客情況。在構建速度模型時，將傳統的卷積運算設置為雙參量，為了適應卷積運算的模板移動，用9 個不同的模板動態實現卷積過程，使模型的有效性和準確性不會受限于車輛行駛速度的多變性。

改進的修正因子考慮了車輛不同時刻軌跡始末點的不同和軌跡的不確定性，對始末點位置進行歸類，并在時間預估模型中起到了一定的優化作用，使預測的通行時間與真實通行時間的精確度達到80%以上，有效地提高了車輛出行安排的合理化和層次化。

基于本文基礎，下一步將對交通狀況更為復雜的可變長路段進行分析建模，嘗試考慮將車輛異常點數據融入數據集作進一步研究，并結合天氣、駕駛員行為、交通信號燈等不確定因素豐富實驗模型，大范圍地模擬真實路網，改進對單一路段預測時間的模型為由出發點到目的地之間的時間預測模型。對城市交通道路時間預測研究奠定更扎實穩定的理論基礎，具有較強的推動力與發展價值。