基于有時間約束的節約里程法對配送線路的優化

劉曉云

(天津工業大學 天津 300387)

近年來，線上、線下超市的增多、產品的多樣化，隨之帶來的是競爭壓力的增大，零售業對供應物流的要求也越來越高。而路徑的優化，很好地解決了低庫存和低運輸成本之間的矛盾。而配送的運作模式是車輛根據事先的路線安排，從超市配送中心出發，前往多家連鎖店進行配貨，最后返回倉庫。這樣既能提高車輛裝載量，又能保證產品的及時供給。不必等到庫存嚴重不足時再進貨，減少了為轉載率而大量進貨的高庫存成本問題，同時給需求量較少的商家帶來了便利，使其在最大程度上實現JIT供給。

一、節約里程法簡述

(一)節約里程法基本原理。節約里程法的基本原理是幾何學中三角形一邊之長必定小于另外兩邊之和。運用到運輸上來說就是依次將運輸問題中的兩個回路合并為一個回路，每次使合并后的總運輸距離減小的幅度最大，直到達到一輛車的裝載限制時，再進行下一輛車的優化。

(二)節約里程法基本條件。節約里程法的運用必須要滿足以下幾個約束條件:(1)每個配送點只能由一輛車來完成配送服務,不可分批配送；(2)配送車輛的最大運載量是固定的,配送車輛不可以超載配送；(3)配送中心的貨物是可以完全滿足配送點的需求,不會出現短缺貨物現象；(4)配送點的數量、配送點與配送中心的距離以及各配送點之間的距離都是已知不變；(5)滿足用戶到貨時間要求。

二、建模背景

(一)研究內容。本文研究的主要內容可以分為三個方面：第一，通過情景假設對A連鎖超市進行實際建模；第二，建立A連鎖超市的目標函數，定義相關變量、約束條件，并用數學公結合超市現有的網點布局，將基于時間窗約束下的節約算法應用于各實際連鎖超市的配送路徑優化中,最終得出A連鎖超市的配送路線優化方案。第三,對配送路徑的優化方法做了歸納性論述，并詳細論述了節約算法，并在此法的基礎上做了有時間窗約束下的優化。

(二)研究意義。本文的研究意義在于：第一，運用節約里程法對A連鎖超市配送路線進行優化，縮短不必要的配送路線，減少配送車輛的調用，降低配送成本，提高連鎖企業市場的競爭力。第二，通過對A連鎖超市的優化分析，可以將本方法推廣到更多的物流配送生活實例中。

三、案例分析與實際建模

(一)模型假設。假設某地區共有5個連鎖超市和一個生活用品配送中心。P0代表配送中心，P1…P5表示分別對應表示1…5連鎖超市的位置。配送中心現在配有4t、6t、10t的貨車，每輛車每次配送的距離被控制在160Km之內。假如車輛行駛時間和配送距離之間有正相關的關系，那么每輛車的均速就會保持在50Km/h。假設配送中心的配送活動從早上5點鐘開始，那么配送量單位為t，裝貨的平均速度為0.5h/t；貨車在預定時間內達到指定地點后停留一段時間，把貨物卸下來。假如每小時可以卸下0.4t的貨物，那么通過計算就能夠得知每個運輸車輛在不同超市的卸貨時間。

(二)模型的建立與求解

1.確立目標函數

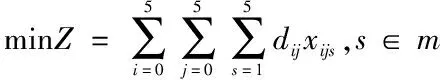
式中：dij,d代表超市i與超市j之間的距離，xijs=1或者0，1表示貨車s從超市i到達超市j，0則代表貨車s從超市j到達超市i；s代表發出車輛的次序；m代表配送中心配備的車輛數，m=4。

2.找出約束條件，根據A連鎖超市的配送情況，確定約束條件為：

aj=1j-1+tj-1

Lj-1=aj-1+wj-1

gj≤aj≤hj

其中：Qs：第s輛車能承受的載重量；e：超市j需要配送的貨物量。

(三)優化分析。第一步，將距離轉變為時間；第二步，使用節約里程法算出各個分店間能省的距離數；第三步，把節約里程按照降序排序；排序處理后的結果見表1。

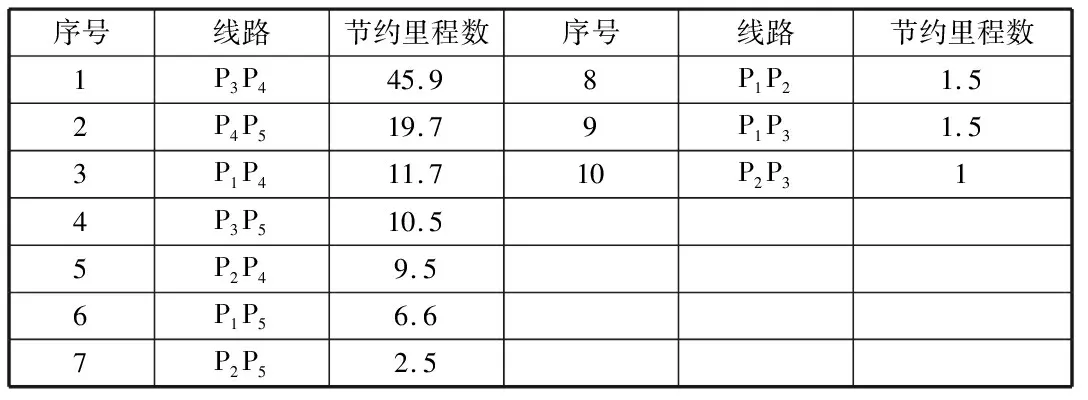
表1

第四步，按照節省距離排序表，裝載量和時間窗的限制明確運輸路線。

(1)第一條線路：P0→P3→P4→P0，可以派一輛最多可以載6t的貨車載5.5t的貨物，運行距離為159.1km，運行距離是小于160km的。

(2)第二條線路：P0→P1→P5→P0，可以派一輛最多可以載6t的貨車載6t的貨物，運行距離為24.4km，運行距離是小于160km的。

(3)第三條線路：P0→P2→P0，見圖1。

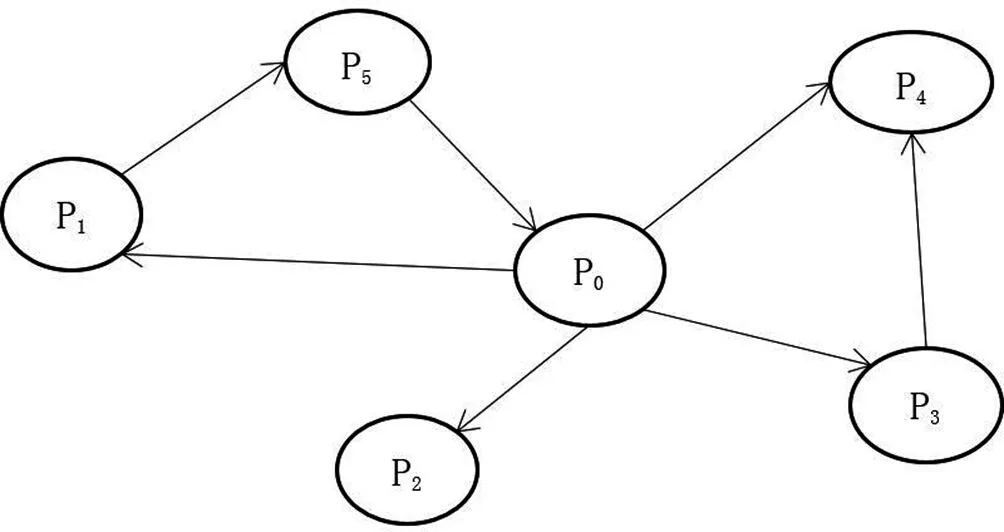
圖1 A連鎖超市優化配送路線圖

(四)優化結果。在考慮到時間窗約束，和運行最大距離、最大載重量情況下，一共提出了三條配送路線，三條線路總行走距離187.5千米，必要車輛是4噸車，6噸車1臺、10噸車1臺，優化后方案節省了52.5千米。

四、結論

配送是倉庫與門店的連接點,在超市運營中發揮著不可或缺的作用。本文從配送路程長短對超市成本影響角度出發，建立基于節約里程法的優化模型，最終較好地節約了超市的配送成本，為超市創造更好的經濟收益。