里德堡原子多體相互作用的研究進展

張正源 張天乙 劉宗凱 丁冬生 史保森

(中國科學技術大學, 中國科學院量子信息重點實驗室, 合肥 230026)

多體量子系統的相互作用是研究量子信息科學必須要解決的瓶頸性問題之一. 里德堡(Rydberg)原子具有很大的電偶極矩, 使得它可以實現長程的相互作用, 為研究多體量子物理提供了有力的技術手段. 因而Rydberg 原子多體系統是多體相互作用探究的理想平臺, Rydberg 原子多體相互作用的研究對多體量子系統的相互作用的性質研究和應用探究有著重要意義. 本文綜述了關于Rydberg 原子多體相互作用方面的研究,介紹了由Rydberg 原子的多體相互作用引起的Rydberg 阻塞效應、Rydberg 原子多體系統拉比頻率的變化以及Rydberg 原子多體系統呈現的特別的空間構型; 同時介紹了利用Rydberg 原子多體相互作用實現一些應用的工作, 如實現單光子源、量子存儲、實時單原子成像以及量子模擬等, 并討論了Rydberg 原子多體系統的研究方向和應用前景.

1 引 言

自然界的很多物理現象本質是多體的, 遵循多體物理的相互作用規律進行演化, 因而對于多體系統相互作用的研究是解析和應用這些物理現象的鑰匙. 而在量子信息科學領域, 如量子計算機、量子通信等量子技術的發展, 都需要在大規模的多體系統中實現糾纏態的制備、存儲與操控等基本技術, 才能實現應用的要求, 這使得多體量子系統的相互作用研究成為量子信息科學必須攻克的課題.目前, 量子信息科學研究較多的多體量子系統有離子系統、中性原子系統、線性光學系統、量子點系統等, 不同的系統有各自的優勢與不足. 其中, 里德堡(Rydberg)原子作為激發的中性原子, 最外層電子被激發至主量子數很高的激發態, 電子軌道半徑很大, 具有很大的電偶極矩. 這使得Rydberg 原子之間的相互作用范圍很大, 可以在原子密度比較稀薄的氣體中實現多體相互作用; 同時, 在主量子數很高的激發態, Rydberg 原子壽命較長, 可以給研究提供便利; 而且Rydberg 原子多體系統的操縱性好, 進一步的較大規模的系統構建也相對比較容易實現, 這些因素使得Rydberg 原子系統成為多體相互作用研究的重要平臺.

十九世紀末, 伴隨著巴耳末公式和Rydberg方程的提出, Rydberg 原子的概念開始建立; 二十世紀后, 玻爾的量子理論和量子力學發展成熟,Rydberg 原子的性質被初步了解, 但是并沒有被廣泛研究; 直到二十世紀七十年代, 人們才開展了大量的Rydberg 原子的相關研究. 通過幾十年的深入研究, Rydberg 原子系統很多有趣的性質被發現, 如Ga?tan 等以及Dudin 等分別觀測到兩原子Rydberg 原子系統的激發阻塞現象[1]和多原子系綜的激發阻塞現象[2]; 德國馬普所的Bloch 研究組[3]基于二維的冷原子激發到Rydberg 原子, 在空間上會形成一種有序的空間結構等. 基于Rydberg多體系統的性質, 相關量子技術的研究也逐漸廣泛與深入, 如量子存儲[4]和量子模擬等. 至今, Rydberg多體系統的相關研究方興未艾.

關于Rydberg 原子多體系統相互作用的性質方面的研究已經在多個方面取得了一定的成果. 通過對兩個原子的集體Rydberg 激發的觀測[1], 可以得到阻塞效應的實驗結果, 也就是兩原子系綜中只允許激發一個原子; 在多原子系綜的集體激發也觀測到激發阻塞現象[2], 有力地說明Rydberg 原子偶極矩的強相互作用導致多體系統具有獨特的整體性質. 當多原子系綜處于激發阻塞狀態時, 系綜的集體拉比頻率會隨著系綜原子數的不同而改變,呈現正比于集體原子數的平方根的規律[1,2]. 由于Rydberg 原子間的強相互作用, Rydberg 多體系統中的Rydberg 原子的分布會出現規律的分布結構[3]. 這些關于Rydberg 原子系統相互作用性質的研究, 一方面為多體相互作用的研究提供了實驗依據, 另一方面也為更大規模的Rydberg 原子多體系統的實現以及應用提供必要的基礎, 推動著量子計算、量子通信和多體動力學研究等領域的發展.

利用Rydberg 原子的多體相互作用, 可以在Rydberg 原子多體系統中實現一系列的技術應用,比如量子存儲、微尺度成像以及量子模擬等. 首先是量子存儲技術, 量子存儲是量子計算和量子通信等不可或缺的基礎技術之一, 也是亟待解決的問題. Rydberg 原子多體系統存在阻塞效應, 可以有效控制阻塞范圍內只存在單激發, 從而實現確定的單量子態的量子儲存[4,5]. 其次, 微尺度成像是物理和化學學科在材料結構等領域的研究中的重要工具, 對成像技術尺度的要求隨著研究水平的發展不斷提升. Rydberg 原子偶極矩的強相互作用會導致在激發阻塞范圍內原子的能級偏移, 從而引起系統的電磁感應透明(electromagnetically induced transparency, EIT)的明顯變化, 利用這個變化, 可以實現光學的非破壞性的單原子成像[6].此外, 耗散是物理系統普遍存在的現象, 耗散過程有一定的規律, 關于耗散系統性質的研究是解析耗散物理系統演化規律的必然要求; 量子模擬和量子計算中廣泛地應用耗散系統, 耗散系統性質的研究將為這些課題提供應用的基礎理論. 外源光子與存儲于Rydberg 原子多體系統的光子相互作用, 存儲光子發生退相干, 在這一耗散過程中, Rydberg原子多體系統具有退相干保護機制, 只有第一個存儲激發發生退相干, 在系統中可以實現單光子減法[7], 體現Rydberg 原子多體系統在耗散過程的獨特規律.

中性原子具有純凈的原子核和外層電子, 形成的原子超精細能級易操控, 這使得Rydberg 原子多體系統相互作用的操縱性良好, 從而使得Rydberg 原子多體系統成為多體動力學相關課題的重要研究平臺. 首先是量子模擬, 利用Rydberg原子多體系統構建量子模擬器[8], 可探究Kibble-Zurek 機制[9]等非平衡動力學問題. 其次, 不同的Rydberg 原子密度會導致原子間多體相互作用強度的變化, 對應不同的原子密度, 多體系統將處于兩種不同的相, 處于兩種相的系統多方面的性質差異顯著. 在臨界條件下, 可以探究一些因素引起的系統性質的變化, 從而研究系統相變的過程[10]. 而且, 在相變點附近, 可以觀測到Rydberg原子多體系統的自組織臨界行為[10], 而自組織臨界行為是自然界中許多復雜性例子的核心, 例如森林火災和病毒的傳播等, 研究基于Rydberg 原子的自組織臨界行為將有潛力應用于物理、化學、生物等諸多自然科學領域, 以及社會和金融等領域.

2 Rydberg 原子系統性質

Rydberg 態是指原子或分子的最外層電子躍遷到主量子數n較高的軌道上所形成的高激發電子態, 處于Rydberg 態的原子被稱為Rydberg原子. 由于Rydberg 原子中最外層電子離原子實(原子核和其余的電子整體)較遠, 可以視為在電荷量+e的點電荷形成的庫侖場中運動, 所以Rydberg 原子是類氫原子, 可以運用類似氫原子的公式來表示其物理性質. 如表1[11]所列, Rydberg原子有許多特殊的性質: 1) 原子半徑大. 根據玻爾氫原子模型, 電子的軌道半徑r∝n2, 其中n是主量子數, 由于Rydberg 原子最外層電子對應的主量子數通常很大, 所以Rydberg 原子的半徑很大.2) 易電離. 一般研究的對象是堿金屬原子, 其電離能表達式為[12]其中R*是修正后的Rydberg 常數,n*是有效主量子數, 可以表示為為堿金屬元素的量子數虧損. 由于Rydberg 原子最外層電子對應的主量子數通常很大, 所以它的電離能就很小.3) 相鄰能級差小. 不考慮堿金屬原子能級修正的情況下, 主量子數分別為n和n+1 的兩個能級之間的能量差, 由于高激發態Rydberg 原子對應的主量子數一般很大, 所以兩個相鄰Rydberg 態的能級差較小. 這一特性限制了激發光的線寬, 因為只有當它足夠小時才能將原子激發到想要的Rydberg 態. 4) 壽命長. 對于一般的處于較低激發態的原子, 其壽命一般為10–8s,而高激發態Rydberg 原子的壽命可以達到微秒甚至毫秒的量級, 這為實驗操作提供了很大的便利性. 在只考慮自發輻射時, 激發態原子的壽命正比于主量子數n的三次方[13], 但是對于處于高激發態的原子, 相鄰能級間的能級差非常小, 因此一定溫度背景下的黑體輻射可能會誘導電子發生受激輻射躍遷, 進一步縮短激發態原子的壽命[14,15].

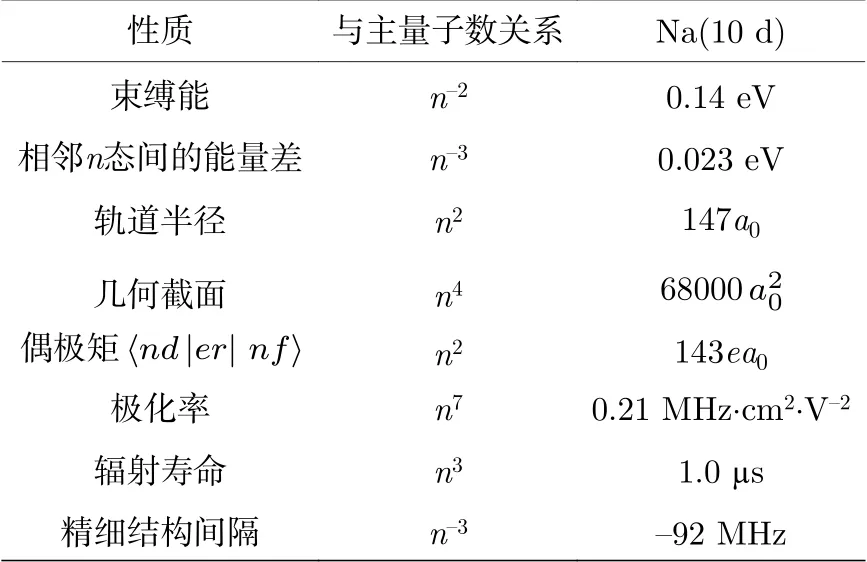
表1 Rydberg 原子的性質和主量子數的關系[11].Table 1. Relation between the properties of Rydberg atom and its principal quantum number[11].

如上所述, Rydberg 原子的半徑大、能量高、能級差小、壽命長, 因此Rydberg 原子多體系統和一般的原子多體系統相比有很大的不同. 以下將簡述由Rydberg 原子間強相互作用所致的激發阻塞效應、空間序結構以及系統集體拉比頻率的變化.

2.1 Rydberg 原子的相互作用和阻塞效應

假設兩個不同原子中的電子相對于各自原子核的位置分別用r1和r2表示, 兩 個Rydberg 原子中心的距離為R. 運用玻恩-奧本海默近似[16]兩個原子構成的系統哈密頓量可以寫為

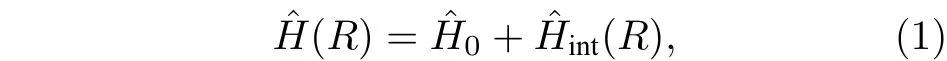
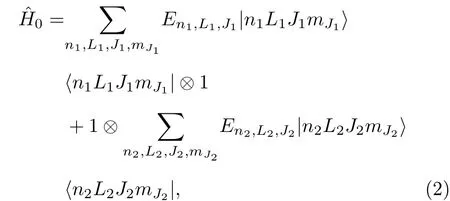
其中En,L,J表示處在態|n,L,J,mJ〉 的Rydberg 電子的能量. 兩個Rydberg 原子相互作用的哈密頓量為

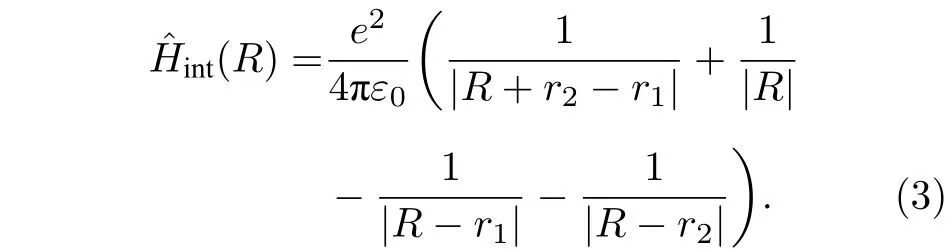
在無外加電場的情況下, Rydberg 原子中電子和原子核的不斷運動會導致正負電荷中心的偏移,從而產生瞬時偶極矩. 所以Rydberg 原子間的相互作用主要是偶極-偶極相互作用. 對于兩個Rydberg 原子, 它們的相互作用能為

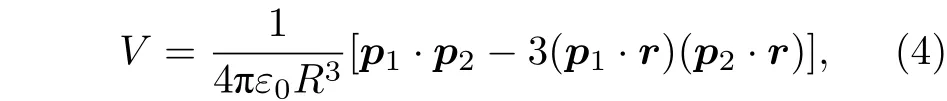
其中R為兩原子之間的距離,r=R/R為原子間單位矢量,p1和p2分別為兩個原子的偶極矩矢量. 假如兩個原子對應的量子態分別為|φ1〉 ,|φ2〉 , 忽略偶極相互作用的角度依賴性, 它們的相互作用能為[17]

假設兩個原子初始時均處在|nl〉態, 它們在偶極-偶極相互作用下會耦合到一系列雙原子態, 但是只有其中一個雙原子態起主要作用. 例如對于|nS,nS〉態來說, 它和雙原子態|nP,(n ?1)P〉 的偶極矩矩陣元最大, 因此兩原子的相互作用能可以簡化為. 以|nS,nS〉和|nP,(n ?1)P〉為基矢的雙原子系綜總的哈密頓量形式如下:

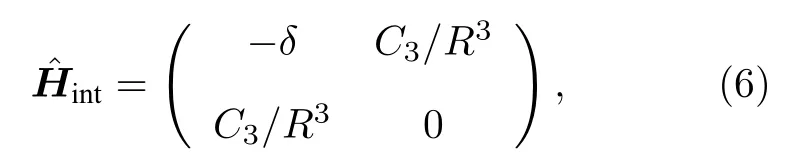
此時稱為范德瓦耳斯作用區; 相反地, 若滿足條件|C3/R3|?|δ|, 則對應能量本征值為?E± ≈±C3/R3, 此時稱為偶極-偶極相互作用區. 為了說明Rydberg 原子強相互作用導致的阻塞效應, 現在考慮兩個原子, 假設原子的基態與Rydberg 態分別表示為|g〉 和|r〉 , 兩態之間的能量差為E, 則兩原子系統對應的態一共有4 個, 分別為|gg〉 ,|rg〉 ,|gr〉 和|rr〉 . 現用能量為E的激光去激發該雙原子系統, 開始時只有一個原子被激發到Rydberg 態|r〉, 由于兩個Rydberg 原子同時存在時會產生強烈的相互作用, 此時雙原子態|rr〉 對應的能量不再是激發單個原子到Rydberg 態對應能量值的兩倍,因此在較強的激光驅動下, 雙原子態能級|rr〉 的偏移值較大, 系統無法從|rg〉 或|gr〉 態躍遷到|rr〉 態,這就意味著在一定的空間范圍內只能有一個Rydberg 原子被激發, 我們稱這個范圍為阻塞半徑. 激發過程如圖1 所示.

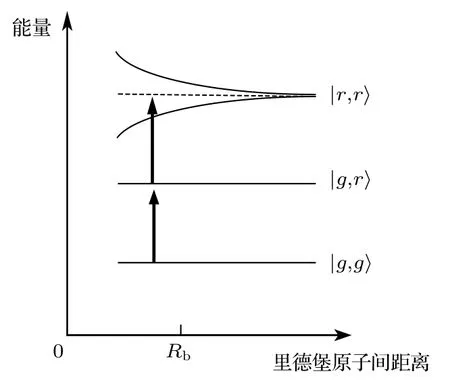
圖1 激光激發兩原子體系能級示意圖Fig. 1. Energy level of two-atoms system excited by one laser.

通過以上分析, 得知當兩個原子被一束能量為E的激光照射時, 系統會被激發到Rydberg 態和基態的一個糾纏態上, 注意非對稱態不與基態耦合,因為該態對應的躍遷偶極矩

根據躍遷定則, 該躍遷是禁止的.

想要觀察到Rydberg 阻塞效應, 采用的激光器線寬不能過寬, 由于Rydberg 能級線寬和激光器線寬都很窄, 激發能譜寬度取決于激發光的拉比頻率, 因此定義阻塞半徑Rb[18]:

在阻塞半徑內, 最多只有一個原子被激發至Rydberg 態.如果激光器的線寬 ?v ??則 要 將(9)式中的?替換為 ?v.

當激發光存在頻率失諧時, Rydberg 原子阻塞效應會有不同的表現形式[19]. 假設頻率失諧量?=wgr ?w, 其中wgr為Rydberg 態和基態能級差對應的角頻率,w為激發光的角頻率, 單原子拉比頻率為?. 運用旋轉波近似, 系統以|gg〉 ,(|gr〉+|rg〉)/和|rr〉 為基矢表示的哈密頓量形式為

對于不同的失諧量和相互作用能, 此系統對應的本征能量有著不同的形式, 例如當?>0 且時系統的本征能量隨Rydberg 原子間距的變化如圖2(a)所示. 其中

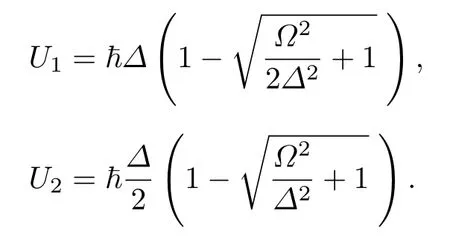
不同失諧頻率和Rydberg 原子相互作用情況下系統的能量隨Rydberg 原子間距變化的關系如圖2(b)所示.

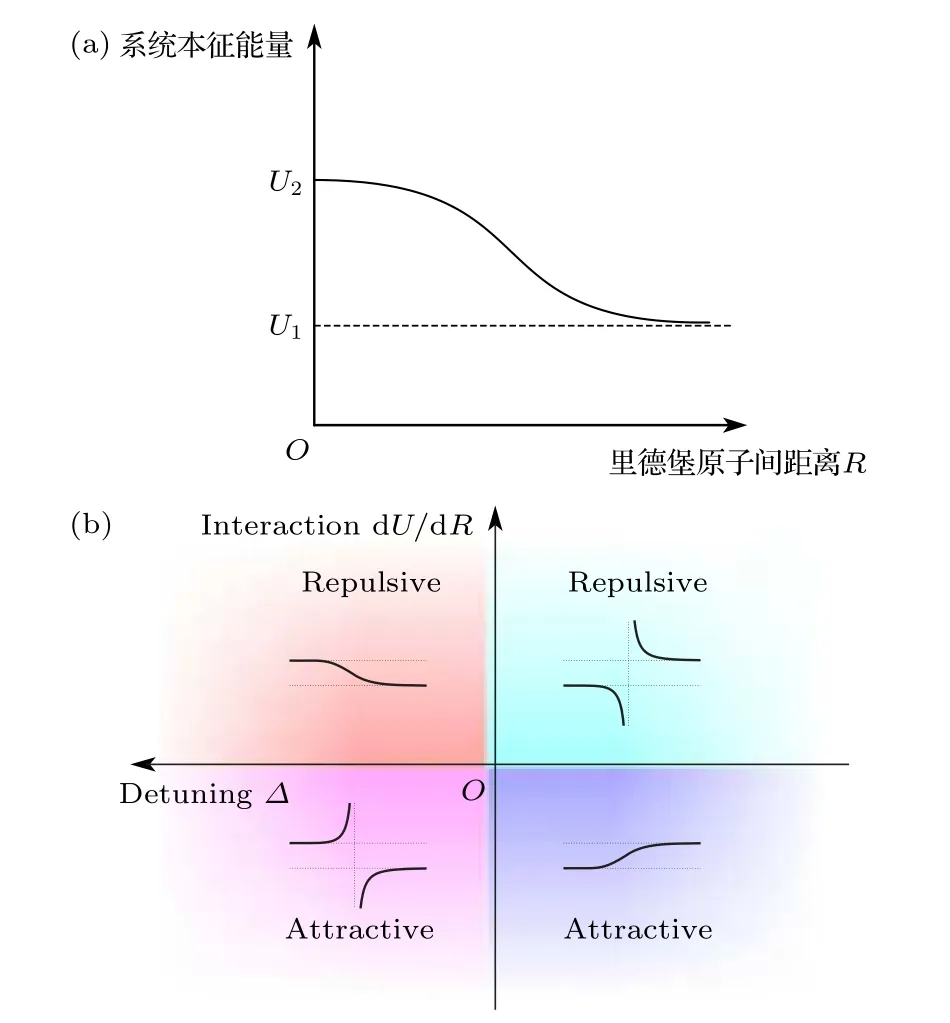
圖2 存在頻率失諧時的雙原子系統能量示意圖 (a) 當?>0 且 d U/d R >0時雙原子系統的能量; (b) 不 同 頻 率失諧和勢能情況下雙原子系統的能量[19]Fig. 2. Schematic of binary Rydberg energy with detuning:(a) The energy of a pair of atoms with ? >0 and d U/d R >0; (b) the energy of a pair of atoms with different detuning and potentials[19].

上面簡述了兩個原子的Rydberg 阻塞效應,如果將情況擴展到N個原子組成的系統中, 當Rb >a時(a為原子系統的尺度大小), 整個原子系統只有一個原子會被激發到Rydberg 態. 假設單個原子的基態為|g〉 , Rydberg 態為|r〉 , 則整個系統的基態為|0〉=|g1g2···gN〉 , 激發態為哈密頓量形式為[20]. 由上式可以看出拉比振蕩頻率會產生倍的增強,這一效應也稱為多體相干拉比振蕩[2].

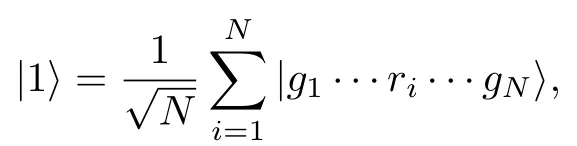
2.2 阻塞效應導致的空間結構

由于Rydberg 原子之間的偶極-偶極強相互作用而導致的阻塞效應, 如果在一個尺度大小與Rydberg 阻塞半徑相當的二維原子系綜中激發基態原子至Rydberg 態, 那么對于不同的Rydberg 原子數應該有不同的分布情況. 例如對于Rydberg 原 子 數Ne=2 的 情 況 下, 這 兩 個Rydberg 原子的連線應該過整個原子系綜的圓心; 對于Rydberg 原子數Ne=3 的情況下, 三個Rydberg 原子應該構成一個三角形, 以此類推, 這一現象直觀地反映了Rydberg 原子的阻塞效應. 來自德國的物理學家Schau?等[3]在實驗上實現了這一物理過程. 他們將旋轉不變的諧波約束勢作用在二維銣原子氣體上, 并將其固定在方形光學晶格中.銣原子初始時刻都處在基態|g〉 , 在激光的作用下被激發到Rydberg 態|r〉 . 系統的動力學由多體哈密頓量控制:

其中矢量i=(ix,iy) 標志著光晶格在平面內的位置. 第一項描述了基態和Rydberg 態以拉比振蕩頻率?的相干耦合,和為轉換算符. 第二項為兩個處于Rydberg 態原子的相互作用勢能項. 在這里它對應排斥力,Vij=, 系數C6<0,rij=alat|i ?j|是兩個在位置i,j處原子之間的距離. 投影算符測量在位置i處的Rydberg 態數目. 這一物理模型忽略了原子的運動和退相干效應, 在大多數情況下是有效的.

實驗制備了150 到390 個簡并87Rb 原子氣體并使其限制在晶格常數alat=532 nm 的光學晶格中, 整個系統的半徑為R=3.5—5 μm[3]. 原子開始時處在基態|g〉=|2S1/2,F=2,mF=?2〉 ,使用雙光子躍遷激發至Rydberg 態|r〉=|43S1/2,mJ=?1/2〉, 中間態為|e〉=|5P3/2,F=3,mF=?3〉 .實驗先通過780 nm 的右旋偏振光將原子激發至中間態, 然后再通過480 nm 的左旋偏振光將原子激 發至Rydberg 態.由阻礙半徑Rb的定義式, 可算出該Rydberg 態的阻礙半徑Rb=4.9 μm. Schau?等[3]用如下方法測量Rydberg原子的激發: 首先用圓偏振共振激光束將去除所有基態原子, 然后通過受激輻射促進Rydberg 原子從Rydberg 輻射到中間態, 最后用高分辨率的熒光成像記錄它們的位置. 實驗通過熒光成像直接觀察退激發的Rydberg 原子, 在單次成像實驗中, 如圖3(a), 三個Rydberg 原子的分布為近似于等邊的三角形的三個端點, 四個Rydberg 原子的分布則是近似為正方形的四個端點, 以及五個Rydberg原子的分布近似為正五邊形的端點. 可以看到處于高激發態的Rydberg 原子不能聚集分布, 而是相互維持一定的空間結構, 這一現象直接體現了原子間長程相互作用所致的阻塞效應. 實驗分析將多次測量得到的空間分布圖進行疊加, 得到多次測量的概率分布(圖3(b)), 并根據系統哈密頓量理論上預測Rydberg 原子的分布情況(圖3(c)). 理論和實驗觀察的結果一致, 這有力地體現了Rydberg原子間強相互作用導致的阻塞效應.

圖3 多體態的空間有序分布圖[3] (a) 直接成像結果; (b) 多次疊加結果; (c) 預測結果Fig. 3. Spatially ordered components of the many-body states[3]: (a) Directly imaging result; (b) accumulative result of many measurements; (c) predicted result.

2.3 相干多體拉比振蕩

一個雙能級系統在一個共振電磁場的作用下會在兩個能級間產生頻率為?的正弦形式的振蕩,這一現象稱作拉比振蕩, 其中?為拉比頻率. 但是如果整個原子系綜只能有一個原子處于激發態, 便會產生頻率為的拉比振蕩, 其中N為總原子數. 由于Rydberg 原子的阻礙效應, 在一個尺度與Rydberg 阻礙半徑相當的系統中, 只會有一個原子處于Rydberg 態, 因此會觀察到相干多體拉比振蕩效應.

對于N= 2 的情形Ga?tan 等[1]于2009 年已經在實驗上發現. 他們運用兩個獨立的光學偶極阱來限制兩個87Rb 原子, 這兩個光學阱之間的距離可以在3—20 μm 之間變化, 精度可以達到0.5 μm.他們先采用雙光子法將87Rb 原子激發到Rydberg 態|r〉=|58d3/2,F=3,mF=3〉 , 在激發過程中需要關閉光學阱來消除激光脈沖外其他光學因素的干擾. Ga?tan 等[1]采用的測量Rydberg 原子激發數量的方法是在脈沖結束后重新打開光學阱時測量光學阱中原子數的減少. 因為當原子被激發到Rydberg 態時, 就有足夠的能量去突破光學阱的限制, 以一定的速度離開光學阱[21,22]. 實驗第一次將兩個光學阱設置的距離為(1.8 ± 0.5) μm. 在實驗中發現同時激發兩個原子到Rydberg 態的概率等于分別激發單個原子到Rydberg 態的概率的乘積,這意味著在18 μm 附近不存在Rydberg 阻塞效應;后來他們又將兩個光學阱的距離設置為(3.6 ±0.5) μm, 這時觀察到同時激發兩個原子到Rydberg 態的概率幾乎為零, 也就意味著進入了Rydberg 阻塞區域. 此時, 實驗測量了Rydberg 激發概率與激發脈沖持續時間的關系, 并與單原子時的情況對比, 發現了激發概率隨激光脈沖持續時間成正弦曲線關系, 且雙原子對應的曲線振蕩頻率約為單原子對應曲線振蕩頻率的倍, 這與理論預期的結果一致.

在接下來的幾年人們只觀察到N= 2 時的集體拉比振蕩, 直到2012 年Dudin 等[2]觀察到了N≥3時的多體拉比振蕩. 當原子系統尺度小于Rydberg 阻塞半徑時, 由于Rydberg 原子的阻塞效應, 原子系統會在基態和激發態

2.4 分析Rydberg 原子多體系綜的理論方法

1) 利用計算機數值解薛定諤方程來得到系統的波函數

為了便于和實驗結果進行比較, 參數選擇應當和正式實驗操作過程中的參數相一致. 在得到系統的波函數后, 便可以計算出系統的許多物理性質,例如激發到Rydberg 態的原子數, Rydberg 原子的空間分布等. 為了便于分析, 將每個原子視為雙能 級 系 統, 假設基態為|g〉,對應的自旋為|↓〉 ,Rydberg 態為|r〉 , 對應的自旋為|↑〉 , 運用旋轉波近似后, 系統的哈密頓量可以寫作[23]:

其中N為系統總原子數,σx,σz均為泡利算符,Vjk是第j和k個Rydberg 原子間的相互作用能,?(t)表示頻率的失諧量,S是激光脈沖的振幅,τ正比于激光脈沖的寬度. 一般的實驗中, Rydberg 原子的相互作用能可以寫成V=?C6/R6的形式. 在進行數值模擬時, 可以運用單一變量法, 控制N,?(t),S,R其中的三個變量不變, 改變剩下的一個變量, 研究系統的物理性質隨該變量的變化關系.

2) 用量子蒙特卡羅方法來求得系統的波函數和總能量

下面介紹廣泛使用的變分蒙特卡羅(variational Monte Carlo, VMC)方法[24]. 以求基態波函數為例, 其主要思想是先選擇一個物理上合理的波函數, 然后通過隨機游走模擬出系統的總能量, 接著改變波函數的值, 得出新的系統能量, 若新的系統能量小于最初的系統能量, 則接受這次改變, 否則不接受. 多次改變波函數的值, 直到系統能量達到最小, 此時對應的波函數和系統能量就是基態波函數和基態能量.

3) 密度矩陣重整化群

在處理費米子多體系統時, 量子蒙特卡洛方法會遇到符號問題, 這里介紹另外一種數值計算方法, 密度矩陣重整化群(density matrix renormalization group, DMRG)[25]. 目前DMRG 用于處理一維橫場伊辛(Ising)模型、一維海森伯模型, 以及其中一個維度遠大于另一維度的二維體系等模型,并在量子多體、量子化學等領域有非常廣泛的應用. 在處理一維Ising 模型時, 密度矩陣重整化群的方法能到達非常高的精度. 在處理類似于Ising模型等多體問題時, 最大的問題在于系統希爾伯特空間指數級增加, DMRG 可以通過矩陣奇異值分解的低秩近似壓縮希爾伯特空間. 并且利用稀疏矩陣Lanczos 算法, 利用系統對稱性降低求解時間.

4) 張量網絡

在處理二維及以上的系統時, DMRG 的計算復雜度也在不斷提升, 作為一種替代的方法, 人們提出了張量網絡重整化群等方法. 一維Ising 模型無外場時, 體系的能量與配分函數為

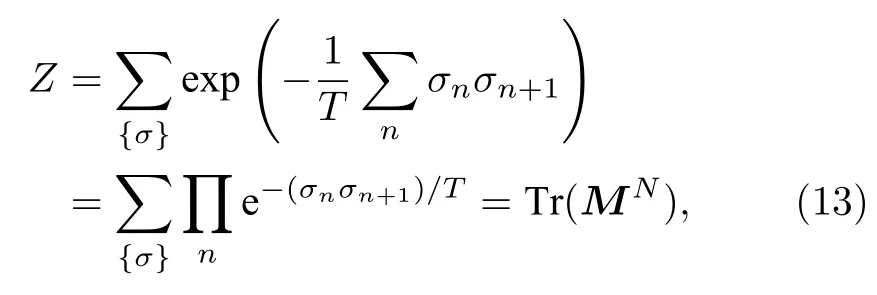
其中Tr 表示求跡運算,M為2 × 2 矩陣, 矩陣元為

在張量網絡中, T r(MN) 可表示為如圖4(a)所示的形式. 其中二指標張量為M. 考慮二維Ising模型, 記溫度的倒數為β, 張量為, 利用周期性邊界條件,配分函數可寫為如圖4(c)所示的形式.

利用張量網絡重整化, 可以得到二維Ising模型的熱容與溫度倒數的關系, 如圖5 所示, 比熱出現尖峰, 且出現尖峰的位置與理論所得β=0.5×ln(1+)≈0.44068679吻合[27].

圖4 (a)一維Ising 模型配分函數的張量網絡表示; (b) 二維Ising 模型配分函數的張量元; (c) 二維Ising 模型配分函數的張量網絡表示[26]Fig. 4. (a) Tensor network form of the partition function for 1D Ising model; (b) tensor element for the partition function of 2D Ising model; (c) tensor network form of the partition function for 2D Ising model[26].

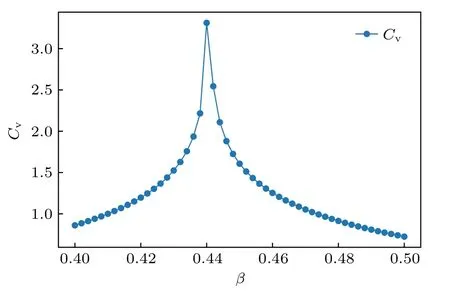
圖5 二維Ising 模型的比熱隨溫度倒數的變化[27]Fig. 5. Relationship between the specific heat and the reciprocal of the temperature[27].

3 Rydberg 原子多體系統應用

3.1 單光子產生器

很多量子的研究中, 單光子都是不可或缺的核心條件. 例如在量子密鑰分發中, 單光子可謂是最關鍵的基礎技術. 由于不可復制原理, 只有實現嚴格的單光子產生器, 才能嚴格保證密鑰的絕對安全. 但是迄今為止, 絕對理想的單光子源仍然沒有實現, 對此的探索也一直是熱門的課題[28,29].2012 年, Dudin 和Kuzmich[30]通過實驗探究了Rydberg 原子系統存儲光子的性質, 實驗結果說明, 當Rydberg 激發態的主量子數足夠高時, 由于Rydberg 原子間的強相互作用, 多原子系統中只出現一個激發, 也就是只存儲單光子, 這為理想單光子產生提供一個方向.

理想的單光子源條件為一定時間內輻射且僅輻射一個光子, 因而, 理想的單光子源需要嚴格抑制多光子聚集, 這也是單光子源質量的鑒定標準.此外, 要求單光子源中的光子具有全同性, 即不可分辨性質; 而且考慮實用性, 高效率和高速率也是需要兼顧的.

對于單光子源質量的定量分析, 可以通過零延時二階自相關強度函數g(2)(0) 衡量. 零延時二階自相關強度函數g(2)(0) 的測量, 一般使用Hanbury Brown-Twiss 裝置, 使用半透半反鏡在光程相同位置分別接出兩個單光子探測器, 然后將光束經過分束鏡, 通過兩個單光子探測器的數據可以計算得到g(2)(0) , 定義為g(2)(0)=p(A,B)/(p(A)p(B)) , 其中A, B 為兩個單光子探測器,p(A,B) 為同時有光子通過兩個探測器的概率. 對于嚴格的單光子源, 一個光子不能分裂, 只能通過兩個探測器的其中之一, 因而 p (A,B)=0 , g(2)(0)=0 ; 反之亦然,g(2)(0)=0體現為光子非聚束, 說明光束為單光子源. 所以對于單光子源發出的光子序列,g(2)(0) 越接近零, 則說明單光子源越理想.

關于光子全同性的分析, 可以利用Hong-Ou-Mandel 干涉[31,32]裝置測量. Hong-Ou-Mandel 干涉是雙光子量子干涉現象, 是指當兩個全同光子以相同光程通過一個分束器, 會發生聚束, 兩個光子完全疊加而變得不可分割, 以至于只能從一個端口出射, 因而在兩個端口設置單光子探測器, 可以測量Hong-Ou-Mandel 干涉. 這個性質可以檢驗兩個單光子源產生光子的全同性, 對于極化平行的兩個光子, 若兩個單光子探測器重合計數為0, 則說明兩個光子具有理想的全同性.

利用Rydberg 多原子系統的阻塞激發效應可以理論上嚴格抑制多光子聚集的現象, 從而產生很高質量的單光子. 光子與原子相互作用, 將原子激發至Rydberg 態, 實現了將光子耦合于Rydberg原子系統中. 由于阻塞效應, 在阻塞半徑區域內,只允許有一個集體Rydberg 態激發, 也就是說明在阻塞半徑區域內只存儲一個光子, 將這個光子讀取出來, 就可以獲得單光子. 只要保證系統范圍足夠小, 理想情況為小于阻塞范圍, 同時保證阻塞效應是充分的, 也即是Rydberg 原子處于主量子數很高的激發態, 理論上可以獲得嚴格的單光子序列.

對于Rydberg 原子系統, 阻塞效應的強度會決定產生的單光子的質量. 利用銣原子Rydberg系統探究激發的單光子的性質, 如圖6 內插圖, 實驗結果[30]表明, 在零延時處, 兩個單光子重合計數很小, 說明激發的光子為非聚束, 體現了因為阻塞效應的存在, 得到的光子序列的單光子性良好. 為了進一步探究阻塞效應對于產生的單光子的性質的影響, 實驗測量了不同的Rydberg 激發態對應的二階自相關強度函數g(2)(0) . 如圖6(a), 實驗結果[30]說明, 隨著激發的Rydberg 態的有效主量子數的增加, 阻塞效應將會越來越明顯,g(2)(0) 越來越接近零, 而當主量子數大于90 后,g(2)(0) 的數值很小, 考慮背景輻射的干擾, 可以視為滿足等于零,也就是說只要激發到足夠高的Rydberg 態, 可以很好地保證產生光子序列的單光子性.

由此可見, 利用高激發態的Rydberg 原子系統, 可以實現質量比較好的單光子源. 但是利用高激發態Rydberg 原子系統實現單光子源, 由于系統的大小實際上往往大于阻塞半徑區域, 同時將光子存儲于Rydberg 原子系統過程的效率不高, 導致單光子源整體的效率很低. 而這個方案所產生的單光子的全同性也有待進一步探究. 綜合而言, 作為單光子源, Rydberg 原子系統在光子質量方面有獨特優勢, 但是效率等其他方面難以達到理想單光子源預期, 目前在單光子源方面總體性能并不優秀, 因此也不作為一般的單光子源的選擇.

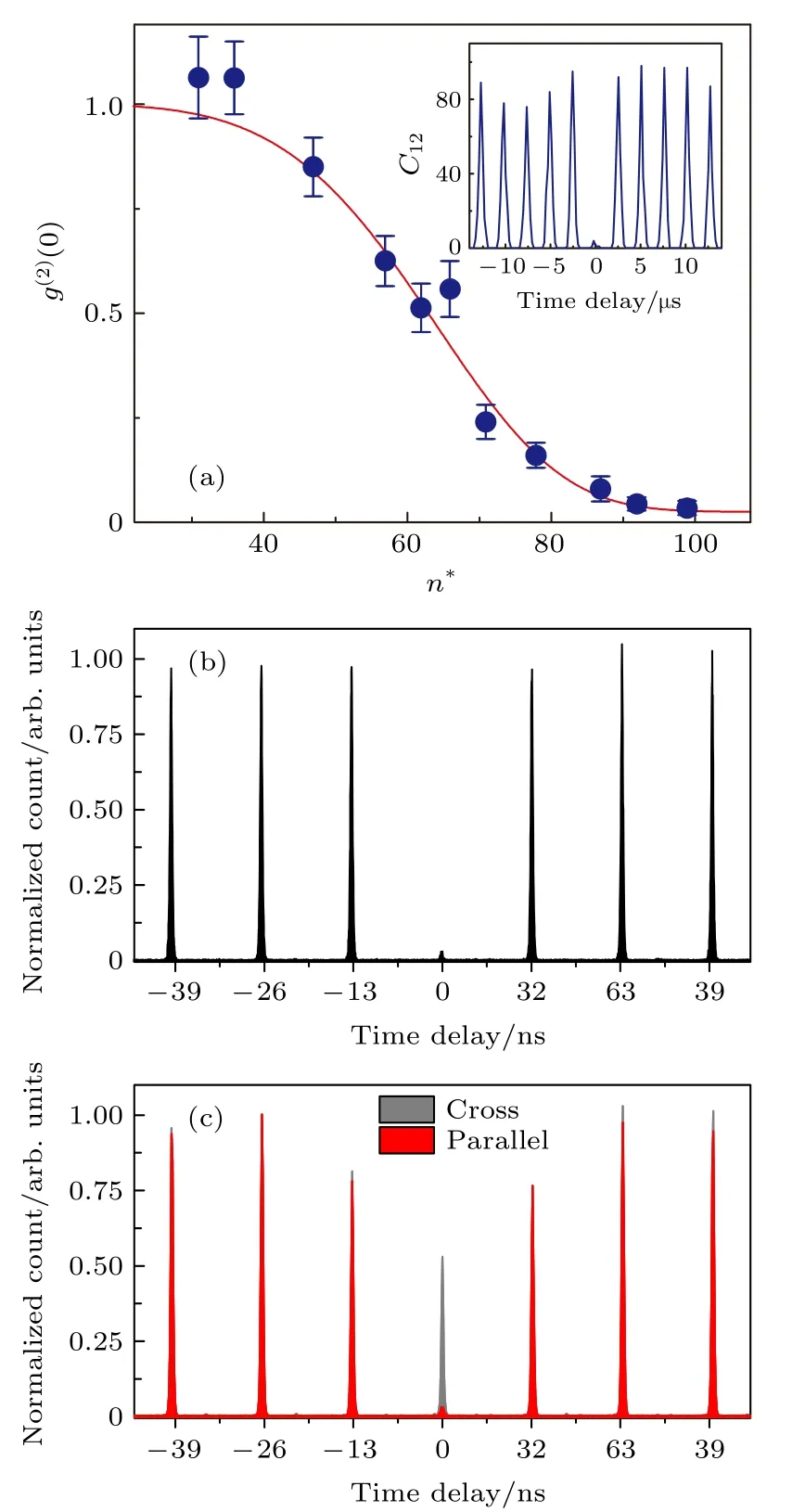
圖6 單光子源性質參數 (a) g (2)(0) 與有效主量子數n*關系[30], 內插圖為重合光子計數與延時關系[30]; (b) 量子點方案中歸一化的重合光子計數與延時關系[28]; (c) 量子點方案中平行和交叉極化情況下Hong-Ou-Mandel 干涉歸一化的重合光子計數與延時關系[28]Fig. 6. Parameters of single-photon source: (a) g (2)(0) as a function of effective principle quantum number[30]. Coincidence count as a function of time decay is showed in the inset[30]; (b) normalized coincidence count as a function of time decay using quantum dots[28]; (c) normalized coincidence count of Hong-Ou-Mandel interference as a function of time decay with parallel and cross polarization respectively using quantum dots[28].

當今利用的單光子源, 有一些更常用的實現方案. 最簡單的方式是直接通過強光衰減實現, 這種實現方法單光子獲取速率快, 而且光子全同性較好;但是衰減無法嚴格控制衰減到單光子的級別, 不可避免出現多光子聚集的情況, 這種方法是無法獲得嚴格的單光子列的, 而且衰減方法自身導致效率很低. 目前實現最優性能的單光子源方案是利用量子點微腔, 量子點方案獲得的單光子質量和全同性都比較良好, 如圖6(b)和圖6(c)所示, 可同時實現97.5%的光子質量和97.5%的光子全同性, 同時該方案的效率可達到60%, 兼顧了單光子源多個方面的良好性質, 是極有應用前景的方案. 這兩種方案由于應用上不同的獨特優勢, 相比基于Rydberg多原子系統的單光子源方案, 應用得更加廣泛.

3.2 量子存儲

量子存儲是量子信息領域的基礎技術之一, 也是量子領域研究的熱點[33?35]. 在長程量子通信[36,37]中, 考慮耗散和退相干因素, 基于光子的量子信息不能直接傳遞到較長距離的需要的地方, 需要有載體實現存儲中繼; 構建量子糾纏和量子網絡[38,39]也需要量子儲存技術作為實現基礎; 此外量子儲存可以用以探測一些其他問題, 如精密測量[40,41]等.

量子存儲的機制, 主要是光與物質的相互作用, 從而實現光子攜帶的量子態相干地存儲于介質中, 即形成確定的介質的量子態, 然后在需要使用時, 可以從介質中讀出攜帶與寫入時相同量子態的光子; 也有比較少采用的方法是在將光子存儲在損耗很小的光路中, 在需要使用時引出. 前者的存儲載體基于介質物質, 主要有固態存儲[34]與原子氣體存儲[42,43]. 作為載體, 其需要具有良好的存儲的性質, 即存儲的效率高、保真度高、存儲的時間盡量長.

原子吸收光子激發為Rydberg 原子, Rydberg原子的壽命與激發態的主量子數有關, 當激發的Rydberg 態主量子數很高時, Rydberg 原子的壽命遠長于一般的低激發態原子. Rydberg 原子的長壽命說明光子可以比較長時間地存儲在Rydberg 原子中, 因而Rydberg 原子符合量子存儲的基本要求. 而且Rydberg 原子多體系統具有激發阻塞的性質, 在一定的阻塞范圍內只允許一個激發, 有利于實現確定的單光子態的存儲. 綜合這兩方面的優勢, Rydberg 原子多體系統是良好的量子存儲載體.

EIT 效應[44,45]是相干光學非線性效應, 是量子非線性光學的基礎課題. EIT 效應是指在三能級系統中, 使用兩種分別對應于能級躍遷頻率的激光入射, 分別稱為探測光與控制光, 當控制光存在時,系統對于探測光不吸收, 即透明現象, 形成吸收峰下陷; 而控制光不存在時, 系統對于探測光近乎全吸收, 形成吸收峰. 利用Rydberg 多原子系統實現量子存儲時, 首先讓控制光射入原子氣體, 利用EIT 效應, 使得本應該對探測光吸收的原子氣體對探測光透明. 讓探測光入射原子氣體, 然后關閉控制光, 原子氣體對探測光不再透明, 而是吸收光子形成集體激發態. 在量子數很高的激發態, 由于阻塞效應, 可以實現確定的單光子態的存儲, 存儲時間之后, 再打開控制光, 探測光從原子氣體中被恢復出來, 實現存儲器的讀出功能.

利用Rydberg 激發態作為EIT 能級有激發態壽命較長的優點, 但是Rydberg 原子多體系統對光子的響應是非線性的[46], 這對量子存儲性質有一定的影響. 在Rydberg 多原子系統中, 如果比較多的原子吸收光子成為Rydberg 原子, 使得Rydberg 原子密度較大, Rydberg 原子之間長程的相互作用會使得系統哈密頓量發生變化, 從而使得EIT 涉及能級發生偏移. 這種情況下即使存在控制光, 系統仍然會吸收探測光, 也即是Rydberg 原子系統中光子與光子的相互作用會破壞探測光的透明條件. 因而實現量子存儲是非線性過程, 存儲效率與入射光子數目、存儲時間和Rydberg 激發態的主量子數有關. Distante 等[47]在實驗上探究了Rydberg 原子多體系統在不同條件下對光子存儲的性質. 實驗結果說明, 隨著入射光子數目的增加,Rydberg 原子偶極矩的相互作用增強, 從而導致系統對于光子存儲的非線性增加, 如圖7(a)所示, 在入射光子數目較少時, 系統的光學線性較好, 而入射光子數目很大時, 系統的光學非線性十分顯著.同時對于Rydberg 原子激發態為|70S1/2〉 的系統,隨著存儲時間的增加, 系統的光學非線性也增強了. 此外, Rydberg 激發態的不同也影響系統的非線性性質, 在主量子數比較低的激發態, 系統響應線性符合良好, 而隨著激發態的主量子數的增加,系統的光學響應非線性顯著, 如圖7(b), 在激發態|26S1/2〉, 系統響應近乎是線性的, 但是對于主量子數40 到70 的激發態情形, 系統的非線性響應就十分明顯了. 通過這一系列實驗的探究, 得到了Rydberg 原子多體系統相互作用對于系統的光學非線性響應性質, 為量子存儲技術的實現與提高提供了理論基礎.

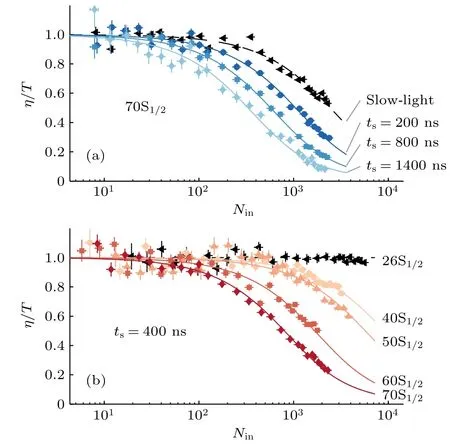
圖7 量子存儲性質隨入射光子數N in 變化[47] (a) 存儲效率與存儲時間關系; (b) 存儲效率與Rydberg 態關系Fig. 7. Properties of quantum storage with different number of input photons N in[47]: (a) Storage efficiency as a function of storage time; (b) storage efficiency as a function of Rydberg states.

基于Rydberg 多原子系統的量子存儲器的存儲時間很短, 主要是在高激發態下系統的量子態很不穩定, 針對這個不足, 考慮基態情況下原子相互作用弱, 基態下原子的量子態穩定, 可以達到很長的存儲時間, 故充分利用基態存儲優勢可以實現比較長時間的量子存儲. 但是基態存儲的問題在于存儲速率很慢, 快速制備容易導致多激發事件, 而利用高激發態的阻塞效應, 通過基態與高激發態的拉比振蕩消除多激發事件, 可以實現快速的單激發[4].存儲過程[4]中, 如圖8(a)所示, 首先通過光泵將系統調節至初始狀態|a〉=|5S1/2,F=1,mF=0〉 , 然后在探測光?p和控制光?c作用下, 系統被激發至狀態|b〉=|5S1/2,F=2,mF=?2〉 , 再給予光場?1將系統激發至高激發態|r〉=|nP3/2,mJ=?3/2〉 ,實現單量子態的存入; 之后如圖8(b)所示, 給予光場?2將高激發態映射至基態|b〉 , 以實現長時間存儲; 經過一定存儲時間, 如圖8(c)所示, 給予光場?r以讀出存儲光子, 并送至后續光子探測器等檢驗裝置. 通過基態與Rydberg 激發態的結合, 可以實現快速制備單激發, 制備激發態時間小于1 μs ;同時實現70 μs 的存儲時間; 但是效率方面比較低,目前未能實現兼顧高效率.

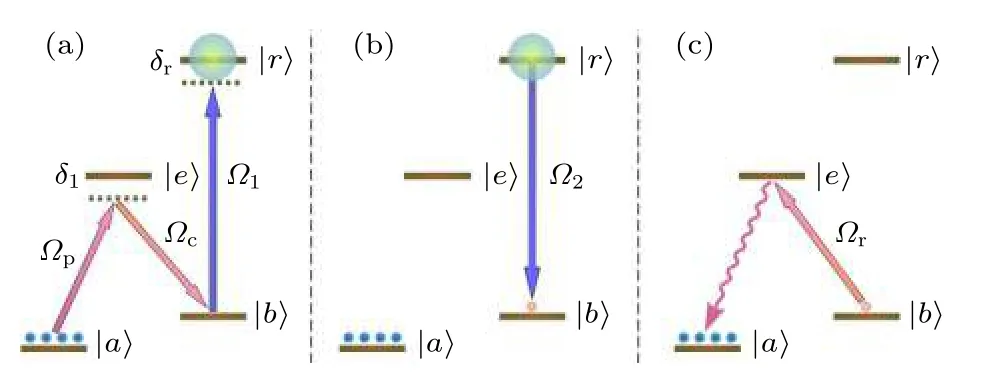
圖8 基態 與激發態結 合能級示意 圖[4] (a) 寫入過程;(b) 基態存儲; (c) 讀出過程Fig. 8. Schematic of energy levels combined exciting state with ground state[4]: (a) Procedure of writing; (b) storage in the ground state; (c) procedure of read.

由于Rydberg 原子間長距離相互作用, 基于Rydberg 多原子系統的量子存儲器還有獨特的存儲性能, 即通過微波場可以控制存儲在Rydberg多原子系統極矩之間的相互作用, 并體現在拉比頻率的變化上[5]. 存儲過程為光子以Rydberg 極矩形式存儲于冷原子團中, 然后用微波場控制極矩間相互作用, 最后, 經過處理的光場被讀出并使用Hanbury Brown-Twiss 裝置中時間解析的單光子計數器檢測. 該實驗存儲過程中與常規存儲的差別在于, 在系統被激發至高激發集體Rydberg 態后,通過微波場使得系統從|60S1/2〉 躍遷至|59P3/2〉 , 實現了對存儲的Rydberg 極矩相互作用的控制, 實驗裝置與其他存儲裝置的不一致也主要在于增加了微波產生器. 這個方法可以實現對存儲Rydberg極矩相互作用的控制, 但是存儲效率較低, 存儲的保真度也不能達到理想存儲器的要求.

基于Rydberg 多原子系統的量子存儲, 可以實現高保真度以及高效率的單量子態的存儲; 同時利用基態與Rydberg 激發態結合的方式, 可以提升存儲時間; 而且利用微波場可以實現對存儲的Rydberg 極矩的控制. 綜合以上, Rydberg 原子系統在量子存儲方面有獨特的優勢, 是探索量子存儲器的一個方向; 而不足在于存儲時間太短, 同時由于應用EIT 效應, 存儲帶寬窄, 而且Rydberg 原子系統的存儲實現大部分需要低溫環境和低噪聲, 環境要求高.

3.3 單原子成像

原子尺度的成像技術是許多課題的關鍵, 擁有足夠分辨率的微尺度成像技術, 很多問題的探究會變得輕松, 如化學反應機理的探究[48]、探索超導材料[49]以及量子邏輯和量子信息處理[50,51]等課題都需要良好的微尺度成像技術的幫助.

而在Rydberg 原子系統中, 利用長程相互作用探測原子位置, 可以達到比較好的空間分辨率,同時可以實現非破壞性的單原子成像, 從而可以觀察原子系統時間演化過程[6].

利用合適的能級, 可以在致密的Rydberg 探測原子氣體中實現EIT, 此時的探測原子氣體, 在控制光的作用下, 對于探測光是透明, 也就是不吸收的. 將高激發態的被探測原子植入致密的Rydberg 探測原子氣體, 對于離被探測原子較遠的區域, 原子間相互作用不受到被探測原子影響, 氣體的吸收性質沒有被改變, 依然保持透明特性; 但是對于與被探測原子相近的區域, 由于被探測原子與探測氣體原子都處于Rydberg 激發態, Rydberg原子的相互作用是長程的, 所以被探測原子與探測氣體原子會存在Rydberg 極矩之間的相互作用,這個相互作用將改變探測氣體原子的能級, 使得能級發生一定的偏移, 而這個偏移將導致這個區域探測原子氣體的透明性質的變化, 從而導致吸收. 如圖9(a)所示, 實驗中, 初始狀態為雜質分子分布在二維探測原子氣體中[6]. 然后通過雙光子(控制光與探測光)激發, 探測原子被激發至激發態|r〉 , 產生EIT 共振, 探測原子對于探測光不吸收. 然而,探測原子與雜質的強相互作用導致臨界半徑區域內吸收光的頻率偏移. 利用雜質周圍原子吸收性質的變化可以實現在吸收圖譜上分析雜質的分布情況, 也就是通過測量探測光的被吸收情況, 可以實現對被探測原子位置信息的確認.

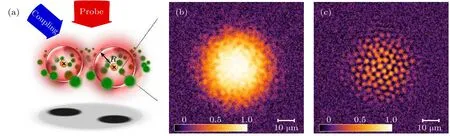
圖9 成像示意圖與模擬結果[6] (a) 單原子成像過程示意圖; (b) 沒有控制光情況下的探測光吸收圖; (c) 有控制光情況下的探測光吸收圖Fig. 9. Scheme of imaging process and simulated results[6]: (a) Scheme of single-atom imaging process; (b) absorption of probe light without control light; (c) absorption of probe light with control light.

Günter 等[6]模擬計算了探測原子氣體對于探測光的吸收的能力的變化, 結果給出了磁化率虛部( Im[χ] )與被探測Rydberg 原子的距離的關系,這是由于磁化率虛部與吸收能力成比例關系, 可以作為吸收能力的體現. 被探測原子對于探測原子氣體吸收的影響, 主要是激發態的被探測原子與高激發態的探測氣體原子之間的Rydberg 極矩的相互作用. 由于被探測原子的存在, 一些探測氣體原子的能級發生移動, 從而使得透明性質發生改變, 也就是吸收能力變化. 由于Rydberg 極矩之間的相互作用是有范圍的, 所以被探測原子的影響也是區域的, 正如阻塞效應中存在臨界區域, 即僅在阻塞半徑之內有阻塞效應, 關于氣體吸收性質的影響也存在著與阻塞半徑相似的臨界半徑, 實驗結果顯示, 在距離被探測原子一定的半徑范圍內, 吸收變得很強, 幾乎接近于1, 說明被探測原子的存在極大地增強了探測光的吸收能力; 而這個范圍外, 吸收能力快速下降, 形成可以明確的分辨的影響界限. 而且實驗結果說明, 與被探測原子處在不同相對位置的探測氣體原子受到的影響是不完全一樣的, 如上所述, 隨著與被探測原子距離的增加, 探測氣體在某一個距離的小范圍內會產生劇烈的變化, 但是并非嚴格的躍變, 因而如果可以充分探究吸收性質隨著距離的變化規律, 有利于更精確地確定被探測原子的位置.

由于被探測原子對于探測光的吸收響應是局域化的, 如果被探測原子密度足夠稀疏, 使得在每個被探測原子自身的響應區域中沒有其他被探測原子, 就可以確定單原子位置. Günter 等[6]利用不同激發態的Rb 原子分別作為探測氣體原子與被探測原子測試單原子成像質量, 結果說明, 在沒有控制光的作用時, 氣體原子對探測光是不透明的, 所以探測原子氣體對于探測光為強烈的吸收, 如圖9(b)所示, 圖中亮度代表吸收程度; 而在控制光的作用下, 氣體原子本應該對探測光透明, 但是由于被探測原子的存在, 使得透明效應失效, 從而在被探測原子存在區域產生吸收, 因而探測光吸收圖中的強吸收部分就是探測的Rydberg 原子的位置, 從而得到被探測原子的空間分布情況, 如圖9(c)所示,圖中亮度代表吸收程度. 模擬結果表明[6]已經可以實現在探測光吸收圖中清晰地辨認被探測原子, 從而得到高激發態的Rydberg 原子形成對稱的分布,這與已知的Rydberg 多體系統分布規律一致[3], 也說明該成像方法可以實用于一些實驗探究.

基于Rydberg 原子系統實現單原子成像也有一些不足, 主要體現在分辨率的限制. 由于如果氣體分子密度過大, 氣體分子之間距離過近, 氣體分子彼此之間存在相互作用, 也會產生能級偏移, 從而形成噪聲干擾, 所以探測原子氣體密度有限制,以至于分辨率也有所限制.

利用Rydberg 多原子系統以及EIT 效應, 可以達到靈敏度高、分辨率較高的非破壞的單原子成像; 不過分辨率存在一定約束限制. 綜合而言, 仍然是單原子成像的一種有力的有效手段.

除了基于Rydberg 多原子系統EIT 的單原子成像, 常用的原子成像技術為通過給予光場使得粒子發生躍遷[52,53], 探測熒光或者吸收結果, 從而分析粒子的位置等信息, 但是這個方法對于躍遷的強度有所要求, 否則得不到探測的效果或者靈敏度和精度得不到保障, 因而有所局限, 即使是利用光腔增強被探測原子與光場作用[54], 空間分辨率也達不到良好的效果. 利用場電離方法[55], 也可以實現原子尺度的成像, 但是這個方法對于樣本是破壞性的, 只能實現一次成像, 而不能持續地探測整個過程.

相比之下, 基于Rydberg 多原子系統的成像方法擁有兼顧非破壞和精確的優勢, 利用這個優勢, 可以探索一些微觀尺度的問題, 例如量子多體的性質或者相關的研究以及單離子成像[56], 在研究中可以提供幫助.

3.4 單光子減法

由于自然中耗散現象的普遍存在, 系統耗散是相當熱門的量子研究對象. 耗散在量子計算[57]、量子模擬[58]和量子通信[59]等研究中有很廣闊的應用. 其中一個應用較多的耗散過程就是單光子減法. 由于Rydberg 多原子系統與光子的相互作用已經比較明確, Rydberg 多原子系統成為多光子存儲的良好載體, 是實現單光子減法的合適的平臺之一.

單光子減法過程, 是一個存儲多光子的系統經過耗散過程, 將損耗且只損耗其中一個光子, 而其他光子維持本身性質. 單光子減法可應用于量子密鑰分發[59]等研究中.

利用存儲多光子的Rydberg 多原子系統的相干保護機制, 在多光子退相干過程可實現單光子減法[7]. 理論研究[7]表明, 在存儲多光子的Rydberg多原子系統中, 外來光場只是破壞第一個激發, 其他激發的相干性不會被破壞, 即系統存在相干保護機制, 這為在Rydberg 多體系統中實現多光子退相干過程, 從而實現單光子減法過程提供了理論依據. 實現多光子退相干過程, 首先將光子存儲在Rydberg 多原子系統中, 原子吸收光子被激發至高激發態, 由于阻塞效應, 系統將處于一定區域內只有單一激發的集體狀態. 當外來光場進入時, 光子之間的相互作用會導致存儲在多原子系統中的光子的相干性發生變化. 通過讀出存儲在Rydberg 多原子系統中的光子可以研究光子相關性的變化. 實驗[7]中通過雙光子將原子從基態|g〉 =|5S1/2, F=2, mF=2〉 通過中間態|p〉 =|5P3/2, F=3, mF=3〉 激發至Rydberg 態|c〉 =|68S1/2, mJ=1/2〉, 實現了將光子存儲在Rydberg 原子系統中, 存儲光子也稱門光子; 而通過雙光子將原子從相同的基態與中間態激發至不同的激發態|s〉=|66S1/2, mJ=1/2〉 , 實現外來光子的存儲制備, 該光子也稱源光子. 而后激發外來光子進入存儲著門光子的Rydberg 原子系統, 通過門光子與源光子的相互作用改變存儲的門光子的性質. 在充分相互作用后, 通過控制光讀出門光子,并通過光子檢測裝置, 通過檢測結果得到多體退相干過程的性質.

如圖10(a), 實驗結果[7]說明, 恢復的門光子數與儲存初始的門光子數間有比較好的線性關系,而實驗條件下, 由于每個門光子散射源光子概率不一致, 達不到理想情況下為1 的要求, 同時源光子數有限, 因而并不是嚴格的破壞單個光子, 但是實驗測量與考慮這些影響因素的理論預測吻合良好,說明理想情況下可以實現性質良好的單光子減法;而這些影響因素也為改進以提升其性能提供了方向上的指引. 實驗結果一定程度上證實該理論的正確性, 也說明該單光子減法方案的可行性.

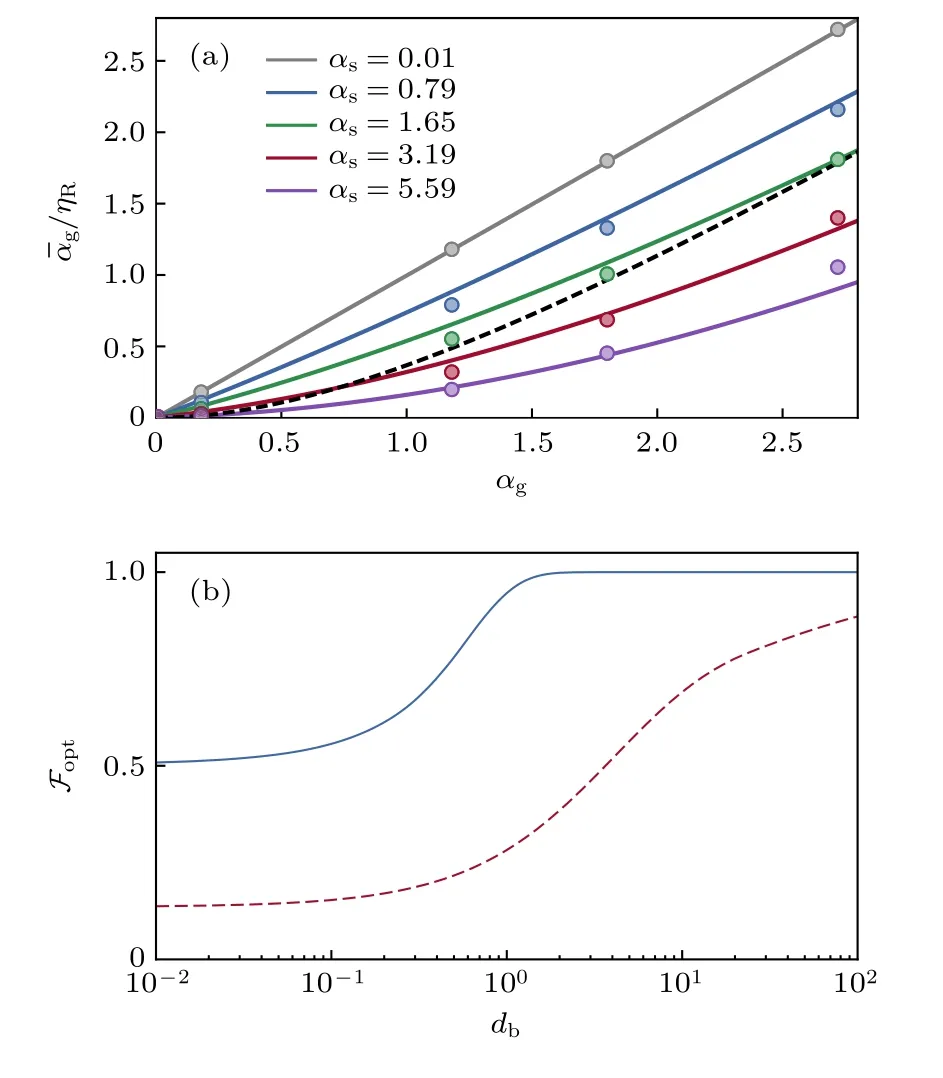
圖10 (a) 不同源光子數情況下, 恢復門光子數與存儲門光子數關系[7]; (b) 最佳減法效率對比[7]Fig. 10. (a) Number of retrial gate photons aˉg as a function of number of stored gate photons a s with different number of source photons a s [7]; (b) contrast of optimal efficiency of subtraction[7].

除了源光子數量和源光子散射概率的約束, 影響基于多體退相干的單光子減法器性能的因素還有光子在Rydberg 多原子系統的存儲與恢復效率,因而, 有關Rydberg 原子系統量子存儲技術的進步, 可以有力推動基于多體退相干的單光子減法器性能的提升. 綜合而言, 由于多體退相干保護機制的優勢, 利用多體退相干實現單光子減法, 是具有前景的方法.

除了多體退相干實現單光子減法, 利用高激發態多Rydberg 原子引起的激發阻塞效應, 還有一些其他可以實現單光子減法的機制, 如讓吸收材料實現單光子飽和[60], 從而實現單光子吸收; 或者利用人造原子與光子的相互作用[61], 實現單光子吸收. 但是飽和吸收實現的單光子減法, 由于阻塞效應的不絕對充分, 存在少量殘余吸收, 也就是并非嚴格的損耗單個光子. 對比基于多體退相干的光學吸收方法與飽和吸收方法的最優減法效率, 如圖10(b), 兩者的最優減法效率都隨著阻塞范圍的增加而上升, 但是基于多體退相干的光學吸收方法的最優減法效率隨阻塞半徑增加很快地增加到了1; 而對于飽和吸收方法, 即使阻塞半徑大幅度增加, 最優減法效率也沒有達到1. 而且在相同的阻塞半徑時, 其他條件相同情況下, 光學吸收方法吸收效率總是要優于飽和吸收方法, 也即說明其減法性能更加良好.

3.5 多體系統演化探究

自然現象中常見的個體都不是獨立隔絕的, 而是在一定區域內與其他個體存在相互作用, 多體系統是自然中大部分現象發生的平臺, 因而對于多體系統性質的研究, 有著深遠的意義. 同時, 很多自然現象的本質是非平衡的, 建立多體系統的非平衡動力學以及探究多體中的臨界相變現象是了解多體系統演化的重要途徑. 對于量子領域, 多體問題的探究[8,9,62,63]也是重要的課題.

對于微觀粒子, 如果粒子之間相距較遠, 一般的粒子的相互作用很弱, 不能直接用作探究多體相互作用時系統的演化規律, 需要其他實驗裝置和步驟實現, 增加了實驗難度; 而高激發態Rydberg 原子之間的Rydberg 極矩相互作用是長程的, 即使粒子間距離較大, Rydberg 極矩間相互作用的范圍可以使得粒子間仍有比較強的相互作用, 可以直接用作探究多體演化.

利用Rydberg 多原子系統, 可以探究量子多體相變問題[62,63]. 由于Rydberg 多原子系統的原子密度不同, 系統可以處于兩種不同的狀態, 即單體無相互作用相(NI-phase)和多體相互作用相(I-phase), 如圖11(a)所示. 當Rydberg 多原子系統處于多體相互作用相時, 系統的EIT 效應會由于原子間相互作用而產生變化, 系統對于探測光的吸收能力發生變化; 同時由于探測光與控制光等外界能量的輸入, 系統并非處于平衡態, 這個變化過程是非平衡的. 實驗[10]探究了在不同頻率的探測光條件下測量了耦合光失諧由負向正和由正向負掃描時電磁誘導透明譜的透射率差, 并將透射率差以參考光場為標準歸一化后作出相圖, 如圖11(b)所示, 所得相圖說明在探測光頻率在一定上升至一定數值時相變出現. 同時, 增加另外一束信號光,同樣方法測定相圖, 實驗結果說明, 相變出現對應的探測光頻率降低, 也即是相變閾值變低, 從而實現了相變閾值的可調節, 為解析多體非平衡動力學的研究提供了幫助.

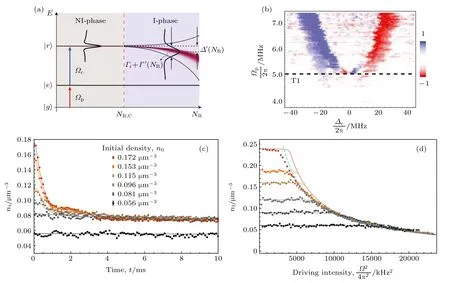
圖11 相圖[10]和自組織行為[64] (a) Rydberg 原子密度相圖; (b) 沒有控制光時EIT 相圖; (c) 自組織演化; (d) 自組織定態規律Fig. 11. phase diagram[10] and self-organized behaviors[64]: (a) Phase diagram of density of Rydberg atom; (b) EIT phase diagram without control light; (c) evolution in the self-organized process; (d) regulation of self-organized stationary states.

利用Rydberg 原子系統, 可以研究多體系統自組織現象. 多體自組織現象是自然普遍的現象,不僅存在于物理領域, 在生物以及經濟等領域都是常見的. 如前所述, 由于Rydberg 原子之間長程的強相互作用以及阻塞效應, Rydberg 原子系統隨著Rydberg 原子密度有無相互作用相(NI-phase)以及相互作用相(I-phase), 這使得Rydberg 原子系統成為探索多體自組織問題的良好平臺. 類比森林火災模型, 可以在Rydberg 原子系統中實現自組織[10], 處于I-phase 的元胞類類比燃燒的樹, 處于NI-phase 類比于沒有燃燒的樹, 以及Rydberg激發耗盡的元胞類比空地, 考慮處于I-phase 的元胞會激發周圍的處于NI-phase 以及Rydberg 耗盡后的再激發等一系列相互作用關系, 類比于燃燒的樹對于周圍的樹以及空地生長樹木等相互作用, 可以得到一些系統的演化規律. 實驗利用包含100×100×100元胞的三維系統模擬,除了包含Rydberg 激發相互作用的元胞會激發周圍NIphase 元胞與I-phase 元胞轉化為Rydberg 耗盡元胞的相互作用之外, 再考慮Rydberg 耗盡的元胞轉化為NI-phase 的概率, 類比于荒地上長出樹木;以及在周圍沒有I-phase 元胞作用下, NI-phase 轉化為I-phase 的概率, 類比于受到火光影響的樹木的自燃, 初始處于I-phase 的元胞比例為0.5, 經過30 次迭代演化, 從實驗過程與結果中分析出自組織的規律[10]. 實驗分析了不同的Rydberg 耗盡的元胞轉化為NI-phase 的概率對于I-phase 元胞形成的集團大小分布的影響, 結果說明, Rydberg耗盡的元胞轉化為NI-phase 的概率越大, 對應的I-phase 集團的最大尺度越大. 實驗分析I-phase集團大小分布與I-phase 集團中元胞數目的冪律行為, 調節Rydberg 耗盡的元胞轉化為NI-phase的概率以及在周圍沒有I-phase 元胞作用下, NIphase 轉化為I-phase 的概率的影響程度, 結果說明, 在后者遠小于前者的情況下, 指數值接近于2;而隨著兩個概率的比值以及各自的值的不同, 指數值不一致, 有對應的規律. 同時實驗模擬結果說明,在森林密度為0.3 左右時存在劇烈的上升趨勢, 近似為突變, 對應于Rydberg 原子系統中, 體現了兩個相的Rydberg 原子密度的臨界點的情況. 關于自組織臨界行為的研究, 實驗總結得到三個臨界標志行為[64]: 第一個是在一定的初始密度閾值之上,系統定態密度趨向于一個固定的值, 與初始密度無關, 如圖11(c)所示; 第二個是定態密度的尺度不變性,體現為在一定的驅動強度之上,定態密度隨驅動強度的關系,可用一個函數描述,如圖11(d)所示;第三個為演化過程,達到定態后,小擾動引起的密度振蕩劇烈,為雪崩式響應,并符合冪率分布.這些行為源于多體系統內部反饋機制,系統在這個機制的作用下可以實現自調節,從而對擾動有獨特的響應行為.這一系列關于Rydberg 多體系統自組織的研究,為多體系統性質的解析總結了部分規律.

利用Rydberg 原子系統,可以研究對稱破缺相變的非平衡動力學[8,62].Kibble-Zurek 機制是對稱破缺相變的非平衡動力學的重要理論,該機制描述了二階相變中拓撲缺陷的形成,即當控制參數接近臨界值時,由系統狀態翻轉的能量間隔確定的響應時間會發散.利用量子模擬器中實現的51 個原子的一維的量子模擬器進行實驗[8],實現了對量子相變中量子Kibble-Zurek 機制(quantumKibble-Zurekmechanism,QKZM)的驗證.

利用Rydberg 原子系統,可以探究光學多穩態問題.光學多穩態是指系統接受一個輸入,但是有多個輸出的現象,是解析非平衡動力學重要研究對象.光學雙穩態作為光學多穩態中的一個分支,在很早已經被關注以及驗證.而Rydberg 原子系統在研究光和物質相互作用方面具有獨特的優勢,是理想的研究光學雙穩態的平臺,通過EIT透射譜非平衡相變觀測光學雙穩態,目前已經在Rydberg 原子系統中觀測到雙穩態現象[10].實驗探究了在不同的探測光拉比頻率情況下,探測光與參考光的透射率差隨著耦合光失諧從紅失諧掃描至藍失諧(由負到正)以及從藍失諧掃描至紅失諧(由正到負)的變化關系,結果說明,在探測光頻率比較低時,透射光譜呈現對稱性,不出現雙穩態現象;隨著探測光頻率的增加,兩個方向的掃描結果不相同,光譜對稱性的破壞,光學雙穩態現象出現.由此可見,利用Rydberg 原子系統可以實現研究光學雙穩態,而且有望作為光學多穩態問題的研究平臺,是研究光學多穩態問題的重要指引方向.

綜上,Rydberg 多原子系統在多體系統演化的探究上有獨特的強相互作用優勢,一定情況下可以簡化部分實驗探究過程,也可以使得探究結果更加顯著.目前利用Rydberg 多原子系統實現了多種多體系統演化問題的研究,為多體動力學相關理論總結了一些基本規律,在未來的研究中,Rydberg多原子系統是多體系統相互作用演化研究的重要平臺.

3.6 多體量子模擬

物理系統模擬是科學研究的重要手段,通過對系統的參數的改變可以獲得系統各方面的因素的影響信息,從而得到系統的性質或者規律,例如經典情況下的分子動力學模擬,已經成為科學研究的利器,在生物化學等許多研究中提供極大的幫助.但是,經典計算機的計算能力極限限制了包含大量個體系統的模擬,這就需要量子系統實現量子模擬.實現量子模擬,主要在于個體間相互作用的控制以及演化時間的限制,超冷原子氣體[65]、分子[66]以及離子系統[67],因為個體間擁有強相互作用,都可以作為量子模擬的平臺.由于Rydberg 原子極大的電偶極矩,個體間相互作用強,作用范圍大,同時利用阻塞作用可以實現Rydberg 原子間相互作用的調節,Rydberg 原子系統成為量子模擬重要的平臺.基于Rydberg 原子的量子模擬[18]最經常探究的課題為Ising 模型的模擬.Ising 模型通常被用于模擬鐵磁性物質、鈷、鎳的結構,并對其在鐵磁性狀態和非鐵磁性狀態之間的相變進行理論描述,且Ising 模型的求解與解決優化問題有關[68].將Rydberg 原子的激發態和基態作為上下兩個不同的自旋態(也可以使用不同的激發態作為兩個不同的自旋態),由于阻塞作用,激發態Rydberg 原子將抑制阻塞半徑內原子的激發,使其保持在基態,實現Ising自旋模型的限制條件;同時,可以通過改變外加光場的參數實現調節阻塞半徑的大小,以及調節原子間距離的大小,從而實現相互作用強度和范圍的調節.目前,借助空間光調制器(spatiallightmodulator,SLM)實現多樣的二維的磁光阱陣列,用以束縛原子,已經可以實現數十個原子二維分布的量子模擬器[63],用于Ising 模型的模擬.利用這個模擬器,探究驗證了當阻塞半徑覆蓋所有原子時,即整個系統僅有一個激發的情況下,系統的拉比頻率與原子數目的平方根成正比,如圖12(a),這個結果與已知的激發阻塞多體系統的拉比頻率規律是一致的.實驗同時探究了在周期邊界條件下,八個環狀原子在不同的相互作用強度下的Rydberg 激發占比以及互相關函數的變化,阻塞半徑為相鄰原子間距離的時候,八個原子可以同時激發至Rydberg 態,所以Rydberg 激發分數為0 至1 的振蕩; 而在阻塞半徑為兩倍相鄰原子間距離時, 由于阻塞效應, 最多僅有四個原子可同時激發至Rydberg 態, 因而理論最高Rydberg激發分數為0.5, 實驗值與之吻合, 但是振蕩頻率增加, 符合拉比頻率的變化; 而當阻塞半徑覆蓋八個原子時, 八個原子作為一個激發集團, 最多允許一個激發, 同時拉比振蕩頻率達到最高. 實驗還探究了在原子數較大時系統的Ising 動力學, 在包含30 個阱的跑道型陣列里裝載20 個原子, 由于每個原子相互作用范圍僅作用兩旁的原子, 所以這是周期邊界條件下一維的自旋鏈, 并非二維結構, 實驗測定了系統的Rydberg 激發分數以及互相關函數,如圖12(b)所示, 實驗結果與計算模擬結果吻合良好; 而在7 × 7 阱方陣里裝載28 個原子情況下, 如圖12(c)所示, 系統的Rydberg 激發分數不再出現振蕩, 與理論模擬預測結果有差異, 系統出現大集團系統的特征. 這一系列二維量子模擬, 為量子多體動力學的研究提供了實驗依據, 也體現了Rydberg 多體系統在量子模擬方面優秀的性能.

圖12 二維量子模擬[63] (a) 不同原子數的集體拉比振蕩; (b) 20個原子系統的Rydberg分數 f R 變 化; (c) 28 個 原 子 系 統 的Rydberg 分數 f R 變化Fig. 12. Quantum simulation in two dimensions[63]: (a) Collective Rabi oscillation with different number of atoms; (c) Rydberg fraction of the systems with 20 atoms; (d) Rydberg fraction of the systems with 28 atoms.

此外, 利用聲光偏轉器形成光鑷陣列, 可以實現包含51 個原子的一維的量子模擬器[9]. 將原子裝載于光鑷陣列中并進行排列, 然后通過給予雙光子場將部分原子激發至Rydberg 態, 等待系統演化時間結束, 通過熒光成像探測系統的最終狀態.熒光成像過程中, 處于基態的原子仍然被禁錮于光鑷中, 而Rydberg 激發態的原子則會逃離光鑷, 形成空缺, 因而熒光成像結果顯示為熒光缺失, 從而確定系統的末態原子狀態分布情況. 實驗觀察探究集體拉比頻率隨著原子數的變化, 以驗證模擬器的基本性能, 實驗結果符合預測, 即拉比頻率與原子數平方根成正比[9]. 同時也探究了13 個原子的一維模擬器在不同相互作用范圍下的狀態的一系列模擬, 在阻塞半徑為相鄰原子距離時, 13 個原子的一維系統最多有7 個Rydberg 激發, 并對應著僅一種穩定分布, 而在阻塞半徑為相鄰原子距離的兩倍或者三倍時, 同樣只對應一種分布, 而實驗的熒光成像結果與預期的結果吻合, 如圖13(a)和圖13(b), 驗證了該量子模擬器對于這個系統的模擬可以演化至最終的狀態, 一定程度上可以實現良好的模擬性能. 實驗探究了基態概率與集體大小的關系, 如圖13(c), 基態概率隨著集體大小呈現接近線性下降關系, 而隨著非指數形式下降, 在51 個原子的情況下, 仍然達到千分之一的量級, 相比于狀態數為2 的51 次方, 千分之一為顯著的增大,這為原子數比較大的量子模擬系統的基態制備可能性以及難度提供了理論上的參考. 實驗著重研究了51 個原子量子模擬器在相互作用范圍為相鄰兩個原子距離下系統的演化, 在51 個原子的集體的18439 次實驗中, 統計了觀測到的狀態數的被觀測次數, 如圖13(d)所示. 其中, 出現最多的狀態為|r1g2r3···r49g50r51〉, 即為通過多體哈密頓量預測達到的終態, 這說明這個包含51 個原子的量子模擬系統在一定程度上可以實現模擬功能. 但是由于系統原子數目較大, 演化到預期狀態需要的時間比較長, 而現在能實現的量子模擬演化時間還不能達到使包含大數目原子的量子模擬器都模擬至最終的狀態, 而提高模擬演化的時間, 也是量子模擬走向應用的最重要的一步. 實驗還討論了51 個原子的量子模擬系統從無序相到有序相過程的相關研究, 有序相即是預期的末態有序分布, 51 個原子的系統理論上只對應一種包含26 個Rydberg 激發的末態分布, 通過對于相變過程的探究, 探究非平衡多體動力學的相關性質.

圖13 一維多原子量子模擬[9] (a) 不同相互作用強度的演化理論結果; (b) 不同相互作用強度的演化實驗結果; (c) 基態概率與系統大小的關系; (d) 出現次數的狀態數的統計Fig. 13. Many-atom quantum simulation in one dimension[9]: (a) Predicted results of evolution with different interaction; (b) experimental results of evolution with different interaction; (c) ground-state probability as a function of system size; (d) number of states with identical number of occurrences.

利用Rydberg 原子多體系統實現多體量子模擬, 是發展量子計算機的基礎研究. 基于Rydberg 原子多體系統的性質研究, 如今已經在Rydberg 多體系統中實現了較大規模的多體量子模擬器, 并且這些系統在規模擴展和操縱性方面擁有很好的發展空間, 指示了量子計算的一個可行的研究方向.

3.7 量子光開關與單光子晶體管

伴隨著量子信息技術的發展, 量子通信與量子計算將漸漸走向成熟, 未來的發展目標將是利用這些成熟的量子技術構建量子網絡, 實現更強的計算和通信能力. 而要實現量子網絡的連接, 量子光開關和單光子晶體管等量子器件是重要的基本模塊.

量子光開關的功能是通過單粒子實現對另一個系統的量子比特的操控或對糾纏的開關態的控制. 很多研究進行了實現量子光開關的探索, 例如單原子的耦合的微諧振器[69], 微型中空光纖中囚禁的冷原子[70], 處于強耦合機制下的腔中的冷原子[71]等. 由于阻塞效應, Rydberg 原子多體系統對于光子響應是非線性的, 可以實現量子光開關功能[72?76].

利用Rydberg 原子系統實現量子光開關, 是通過EIT, 將門控光子存儲在系統中, 由于阻塞效應, 門控光子的激發破壞了目標光子的EIT 條件,實現目標光子的傳輸, 從而實現開關功能. 有關研究提出利用包含一個Rydberg 原子的系統能實現兩光子糾纏門[73]. 而有實驗利用糾纏光子對在兩原子系綜實現了光開關的操作[76], 實驗通過在二維原子云中制備糾纏光子對, 然后輸入到一個三維原子系綜實現光開關, 得到超過50%的開關對比度的結果, 顯示了良好的應用前景.

類似電子電路中電子晶體管, 單光子晶體管的作用便是在量子網絡連接中實現單向導通、整流、放大等信息處理中需要的基本功能. 類比于電子晶體管中微電流控制大電流的功能, 單光子的信號是最微弱的, 單光子晶體管的功能是通過單光子信號實現對多光子的控制, 在量子信息處理中有多種應用[77]. 而在Rydberg 多體系統中, 阻塞效應導致Rydberg 多體系統具有很強的光學非線性, 利用這些光學非線性性質, 可以實現單光子晶體管的功能[78?81].

利用Rydberg 原子系統實現單光子晶體管, 首先是實現傳輸光子的EIT 條件, 使得傳輸的光子可順利通過, 然后單光子入射介質, 形成Rydberg激發, 而Rydberg 原子長程的相互作用將破壞傳輸光子的EIT 條件, 使得能夠透過的光子大大減少, 從而實現了單光子對于多光子的變化的控制,即實現了微小變化的放大, 增益受到阻塞作用的范圍與強度的影響. 實驗利用阻塞效應, 在超冷氣體中觀測到單光子晶體管的增益達到20, 顯示了基于Rydberg 原子系統的單光子晶體管良好的前景[78].有研究則利用Rydberg 原子系統實現的單光子晶體管, 還可以實現單個Rydberg 原子的無損測量,保真度達到0.72[79]. 而通過斯塔克調頻的F?rster共振可以增強相互作用[80], 可將增益提升至超過100, 同時對單個Rydberg 原子的無損測量保真度超過0.8. 此外, 有研究提出基于腔量子動力學(cavity quantum electrodynamic, CQE)的單光子晶體管的方案, 數值模擬結果顯示可以達到抑制上千個光子[81].

綜上, 基于Rydberg 原子系統實現的量子光開關和單光子晶體管擁有相當良好的性能, 是值得深入探究的方向, 尤其是單光子晶體管的性能的快速提升, 體現了極有潛力的應用前景.

4 總結與展望

現在的物理學, 已經進入了量子的時代. 探索量子領域的種種問題, 成為物理研究的主要課題.Rydberg 原子由于高激發態形成很大的電偶極矩,擁有范圍和強度遠大于一般基態原子的相互作用,是理想的量子課題探究平臺. 同時, Rydberg 多原子系統中存在阻塞效應, 給Rydberg 多原子系統賦予了獨特與光子相互作用的性質. 利用阻塞效應, 通過Rydberg 多原子系統可以實現單光子源、單光子減法器、單原子成像和量子存儲等一系列量子領域研究中的基礎問題, 為其他更進一步的研究做好鋪墊.

Rydberg 原子系統在多體問題的探究中有很大的潛力, 由于原子間強的Rydberg 極矩相互作用, 在量子光開關、量子模擬、多體自組織行為等研究中有獨特的實驗優勢, 為非平衡動力學的解析等探究提供一些基礎和方向.

目前, Rydberg 多原子系統的探究主要有兩個方向[18]: 一個是增加系統的Rydberg 原子的數目,大集團的Rydberg 原子系統才能實現更強大的量子模擬, 突破經典模擬的計算能力; 另一個是發展不同的原子, 目前的Rydberg 原子主要是堿金屬原子, 是具有一個價電子的類氫原子, 研究具有兩個或多個價電子的Rydberg 原子多體系統[82,83],能實現更加復雜的量子模擬和計算等應用. 此外,基于Rydberg 原子進行的其他方面的研究工作也不少, 如Rydberg 聚分子[46], 在Rb[84], Cs[85], Sr[86]方向都有了突破性的工作; 在基于Rydberg原子系統的拓撲相的研究中也有一定的研究成果[87,88]; 還有Rydberg 原子系統中的結晶現象[89,90]的研究等.

關于量子領域的研究方興未艾, Rydberg 多原子系統由于獨特的性質, 有著廣闊的應用前景[18],可以應用于求解最優化問題[91], 如圖論中的組合問題, 即求圖的最大獨立集[92]; 以及通過Rydberg多原子系統和經典計算機的結合, 實現變分量子模擬[93]等.