大噸位主捆綁機構力-熱耦合特性研究

張 薇，顧名坤，容 易，秦旭東，趙 婷

（北京宇航系統工程研究所，北京，100076）

0 引 言

捆綁式運載火箭借助于捆綁結構將助推器連接在芯級周圍，能夠大幅提高起飛推力，增強火箭運載能力，節約火箭發射成本[1]。有研究表明，固體捆綁式助推器可使得火箭運載能力提高70%左右[2]，對于大型運載火箭，捆綁結構的可靠性是一項關鍵技術[3]。一種基于球頭-球窩配合的捆綁結構普遍應用于捆綁式火箭芯級與助推器的連接，作為傳遞發動機軸向力的主傳力結構，它既能夠傳遞較大載荷，又能適應裝配時助推器與芯級的位置與角度偏差。

在飛行過程中，由于高速氣流和發動機推力的作用，助推器相對于火箭芯級發生轉動，導致捆綁結構中的球頭-球窩在傳遞較大載荷的同時發生相對轉動，球頭-球窩接觸面之間產生相對摩擦[4]。根據工程估算，摩擦面接觸壓強高達到上千兆帕，摩擦會導致局部溫度急速上升，降低材料的強度，從而影響捆綁結構的承載能力。因此，在多項載荷作用下，球頭-球窩配合結構的接觸摩擦生熱對結構強度的影響成為捆綁結構設計的一個關鍵因素。

1 捆綁結構模型

典型球頭-球窩配合捆綁結構，球窩與芯級捆綁連接座相連，球頭與助推器捆綁連接座相連。在飛行過程中，球頭與球窩允許發生微小的轉動，適應助推器與芯級之間的相對變形。在飛行過程中，球頭受到助推器的作用，產生3 個方向的推力，通過球頭-球窩配合結構傳遞給芯級連接座，從而推動火箭芯級上升。

2 摩擦生熱計算方法

球頭-球窩在相對轉動過程中的，接觸面處存在較大的摩擦力，摩擦力與接觸壓力和摩擦系數存在著密切關系，因此要分析摩擦生熱，首先必須分析接觸面上的接觸壓力。

對于彈性固體接觸模式，Hertz 給出了不同形狀物體接觸時，接觸面處的變形和接觸區域大小計算方法[5]（Hertz 接觸模型如圖1 所示）。在集中載荷zF 的作用下，假設球窩的標稱半徑為R。假設結構材料相同，泊松比為0.3，球頭-球窩接觸形式的嚙合深度δ 可以表示為

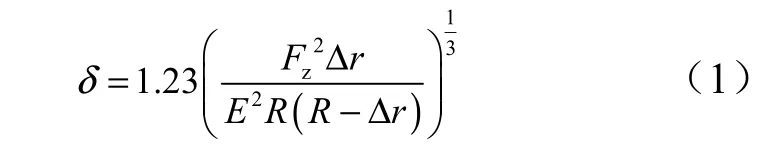
式中 rΔ 為球頭與球窩半徑之差；E 為材料彈性模量。

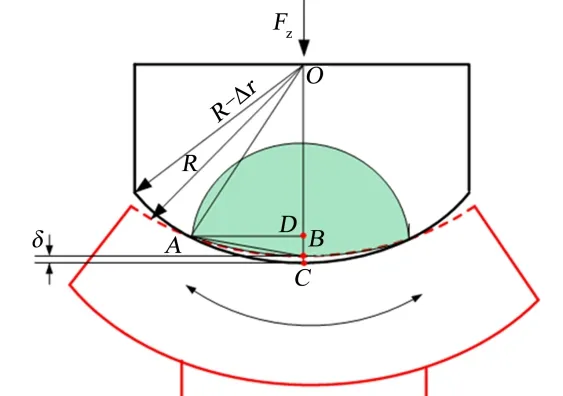
圖1 球頭-球窩Hertz 接觸模型Fig.1 Hertz Contact Model of Ball-head and Ball-pocket

根據Hertz 接觸模型，球頭-球窩接觸區域的橫向長度2a 可以表示為

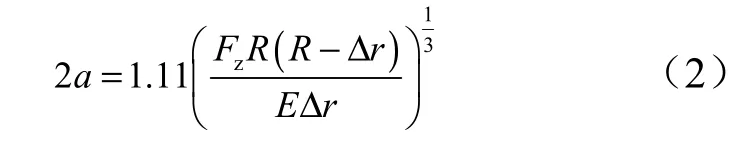
那么球頭-球窩在接觸面上的平均接觸壓力就可以表示為

式中 ε 為接觸面積修正系數，取0.38。

球頭-球窩摩擦接觸過程中的轉動頻率為f，球頭發生周期轉動的最大轉角幅度為θ（弧度制），接觸面上的相對運動的平均速度v 可以表示為

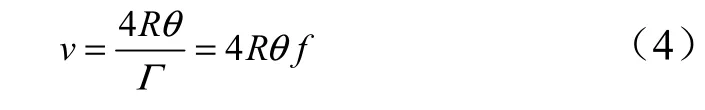
式中 Γ 為轉動的周期。

接觸面上的摩擦生熱速率可以表示為

式中 PW為生熱速率；μ 為接觸面摩擦系數；S 為摩擦面積，即球頭與球窩的接觸面積。

如圖1 所示，在球頭-球窩結構受力變形后，接觸區域可以近似等效為以球面弧長為半徑的球面，設的弧長為 b，由于變形非常小，所以可以認為b =≈ AB ，根據幾何關系可以得到：

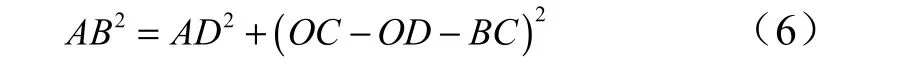
在小變形條件下，計算過程中忽略δ 和 rΔ 的二階小量，那么可以得到：

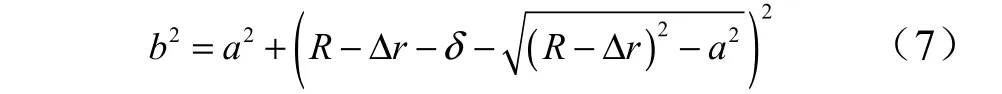
局部摩擦生熱面積可以表示為

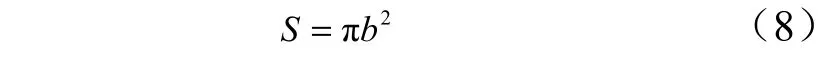
將式（4）和式（8）代入式（5）中可以得到：

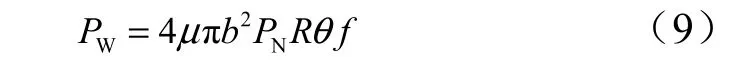
在極短的時間內，假設球窩與球頭接觸帶溫度變化率可以表示為

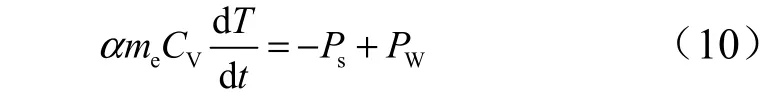
式中 me為球頭-球窩接觸帶吸熱的材料等效質量；α為質量修正系數；第2 項為接觸帶周圍散失的熱損失；VC 表示材料的比熱容。

參考集中參數法[6]，散失的熱量與導入熱量擬合為

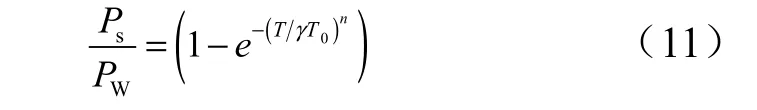
式中T0為參考溫度， T0=273 ℃；n=0.2。

球頭接觸面溫升區域可以近似等效為圓錐體，那么其可以表示為

式中 h0為等效圓錐體的高度。

將式（12）帶入式（10）中，可以得到：

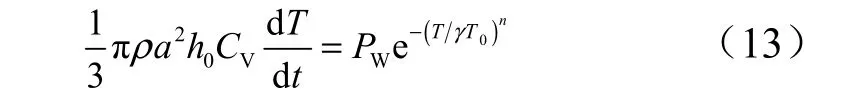
將式（11）和式（12）代入式（13）進一步化簡可以得到溫升與接觸壓力的變化關系為

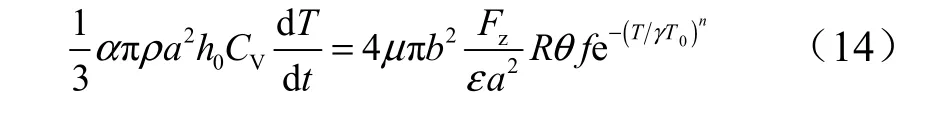
將式（3）和式（9）代入式（13），那么溫度的上升速率就可以表示為

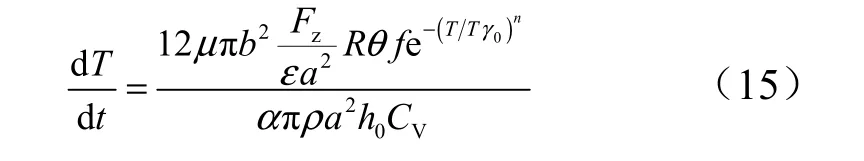
上式反映溫度與球頭-球窩半徑之差的關系，其中包含在計算平均壓力的面積修正參數ε、在計算溫升變化時用于修正溫升區域的等效材料質量的參數α 和用于修正熱散失項的參數γ 。

3 有限元分析模型

沉淀硬化不銹鋼PH13-8Mo 是一種超高強度的不銹鋼，常溫下的屈服極限達到了1517 MPa，楊氏模量為200 GPa，泊松比為0.3，其強度和熱力學參數隨溫度的變化如表1 和表2 所示。可以看到當溫度超過400 ℃時，材料強度迅速下降。

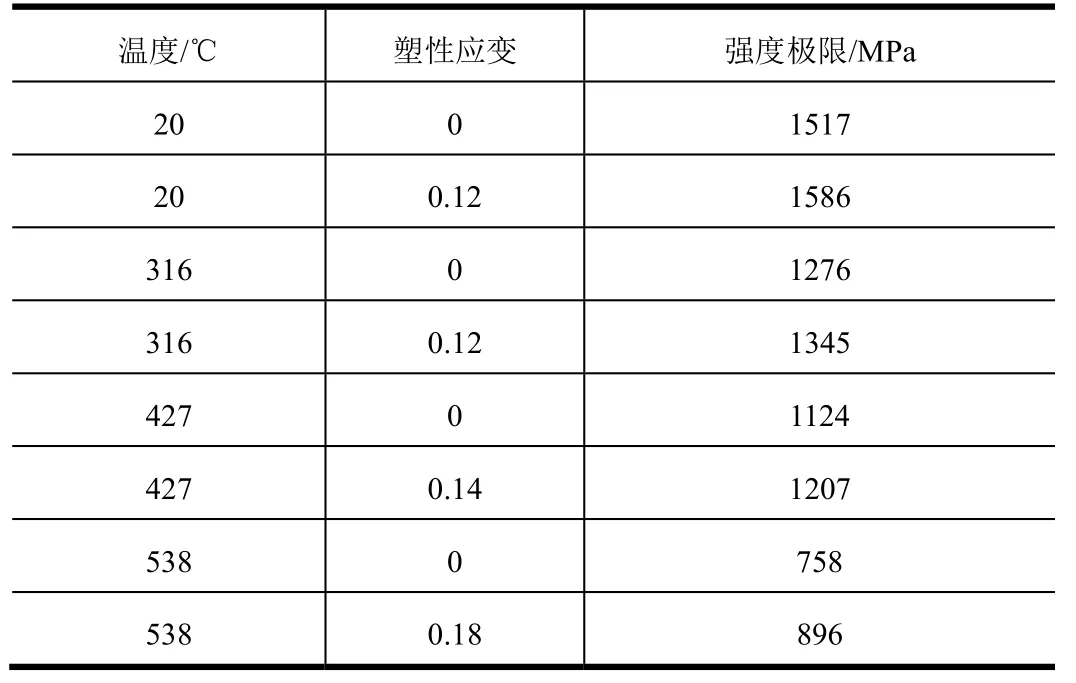
表1 材料力學參數Tab.1 Mechanical Parameters

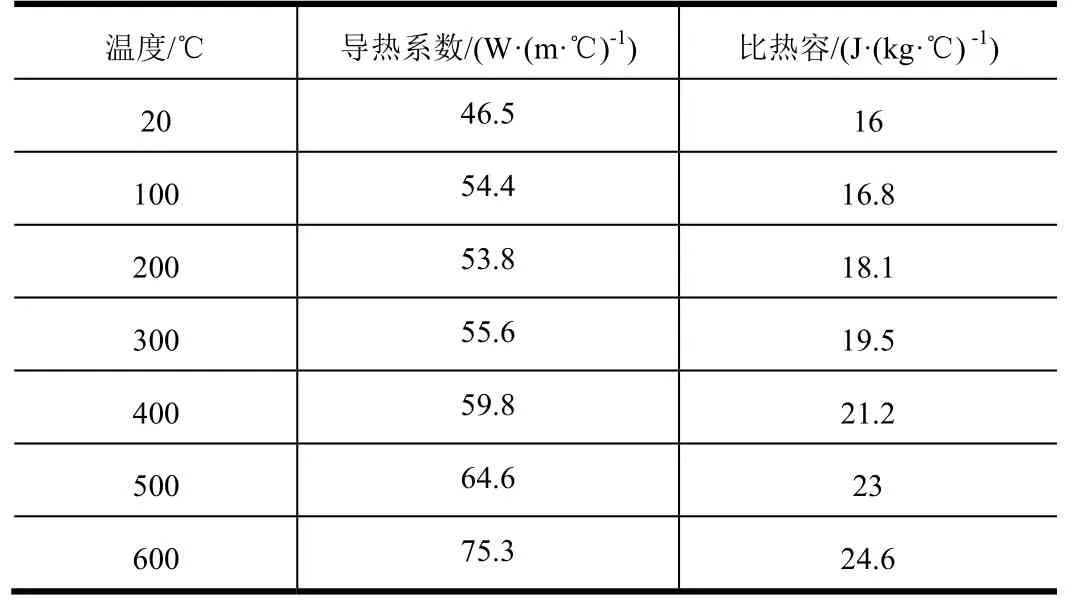
表2 材料熱學參數Tab.2 Thermal Parameters

火箭飛行過程中球頭-球窩作用時間大約為150 s，3 個作用力隨著推進劑燃燒和飛行速度的增大逐漸變化，整體模型采用熱力耦合算法，將會消耗大量的計算時間。在不影響分布情況下，將模型簡化，基本網格尺寸為5 mm，接觸面處進行網格加密，最小基本網格尺寸為2 mm，生熱計算過程單元類型為C3D8RT。根據局部生熱溫度變化，將材料模型等效為隨載荷變化的參數，并進行3 項載荷作用下的強度計算。

4 球頭-球窩轉動生熱分析

根據上述描述，首先分析不同球頭-球窩半徑匹配對摩擦生熱的影響。施加載荷Fz，給另一端施加周期轉動，轉角幅值為2°，頻率分別為2 Hz、5 Hz 和8 Hz。當球窩直徑保持不變時，球頭直徑變化會影響到接觸面積的大小，導致作用到球窩的壓力變化，最終影響到生熱速率的改變。分別對球頭半徑為75 mm、74.9 mm、74.8 mm、74.7 mm、74.6 mm、74.5 mm 與球窩半徑為75 mm 模型進行數值分析，分析時間為10 s，加載壓力為1 733 266 N。

4.1 球頭半徑對接觸壓力的影響

圖2 表示接球頭-球窩接在集中載荷作用下，球窩表面的接觸壓力分布云圖。根據接觸壓力分布云圖可知，當球窩與球頭半徑都為75 mm 時，邊緣承受較大的接觸力，最大接觸壓力為654 MPa；當球頭半徑減小0.1 mm 時，最大接觸力出現在球窩中心，此時接觸壓力為956 MPa，隨著球頭半徑減小，球窩與球頭的接觸面積減小，接觸壓力增加；當球頭半徑為74.8 mm時，球窩邊緣的接觸壓力已經變為0 MPa，此時說明球頭-球窩已經不再是完全接觸。

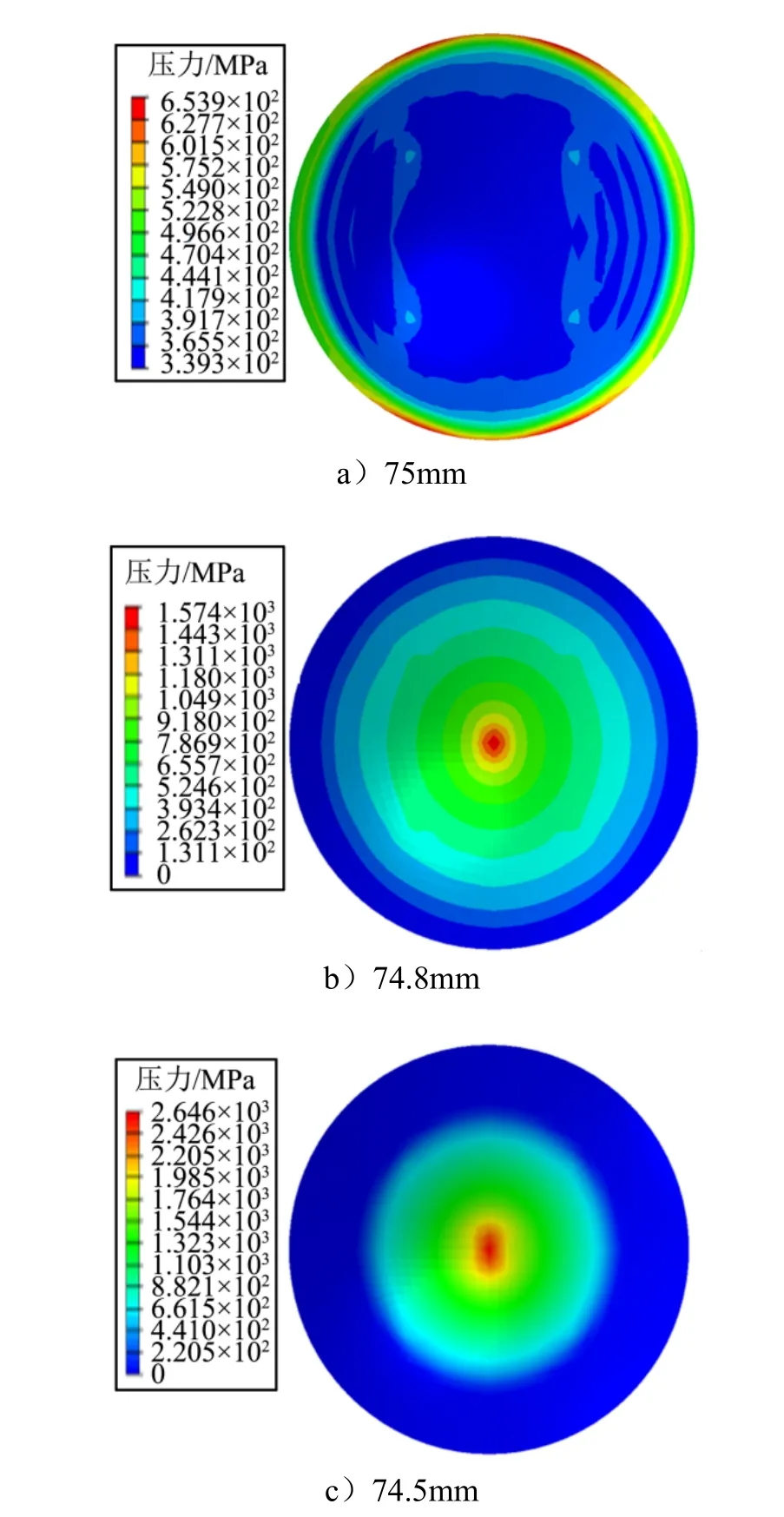
圖2 接觸壓力分布云圖Fig.3 Contact Pressure Distribution Nephogram

提取球窩中心的接觸壓力繪制接觸壓力隨半徑的變化關系如圖3 所示。由圖3 可以看出，球窩接觸壓力隨著球頭半徑的減小呈線性減小，且通過式（3）計算的接觸壓力能夠很好與仿真值吻合，標定面積修正系數為0.38。

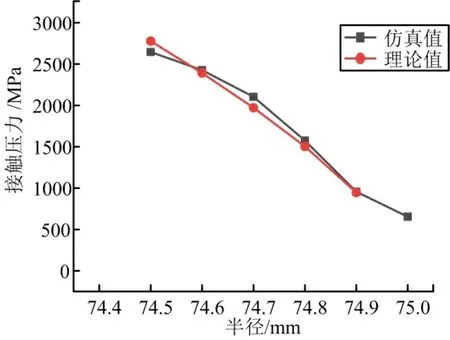
圖3 接觸壓力與半徑的變化關系Fig.3 The Relationship between Contact Pressure and Radius

4.2 球頭半徑對溫度分布的影響

球頭-球窩配合球面半徑標稱值為75 mm，球頭半徑變化導致接觸狀態的改變，通過仿真計算出了轉動頻率5 Hz 狀態下，結構溫度隨時間變化規律，如圖4所示。由圖4 可以看出，隨時間變化，結構溫度逐漸升高；球頭半徑越小，結構溫度越高，說明球頭與球窩的匹配性越差。通過仿真結果對參數進行標定，標定結果為 γ = 0.001。

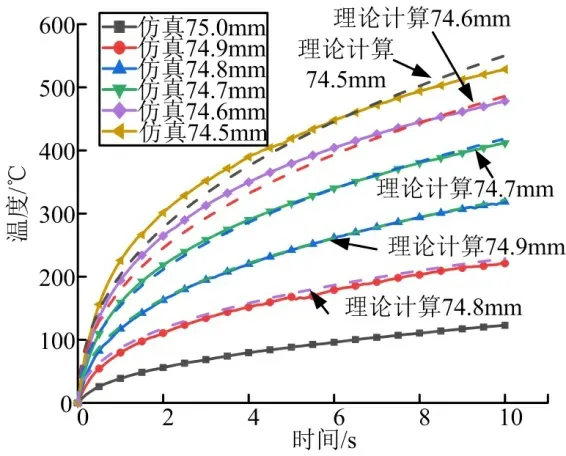
圖4 不同球頭半徑結構溫度變化曲線Fig.4 Temperature of Structure with Different Ball Head Radii

圖5 給出了球頭半徑分別為74.5～75 mm 狀態下的球頭-球窩的溫度場云圖。從圖5 中可以看出，隨著球頭半徑的減小，接觸面積減小，溫度分布區域減小，說明74.5 mm 時，球頭-球窩接觸面積較小，受熱結構體積較小，故溫度最高達到529 ℃。當球頭半徑為75 mm 時，溫度基本均勻分布于整個接觸球面上，最高溫度為136 ℃，溫度相對于其他較低。當球頭半徑為74.9 mm 時，最高溫度為212 ℃，整個球面的溫度都上升，但溫度不再均勻地分布于接觸球面上，呈現中心溫度高，邊緣溫度低，與75 mm 球頭相比，球頭半徑為74.9 mm 時，邊緣溫度為92 ℃，當球頭半徑為74.7 mm，球窩邊緣的溫度未發生變化，這是由于此時球窩邊緣不與球面接觸，同時球頭-球窩內部產生的熱由于時間太短也無法傳到其邊緣處。

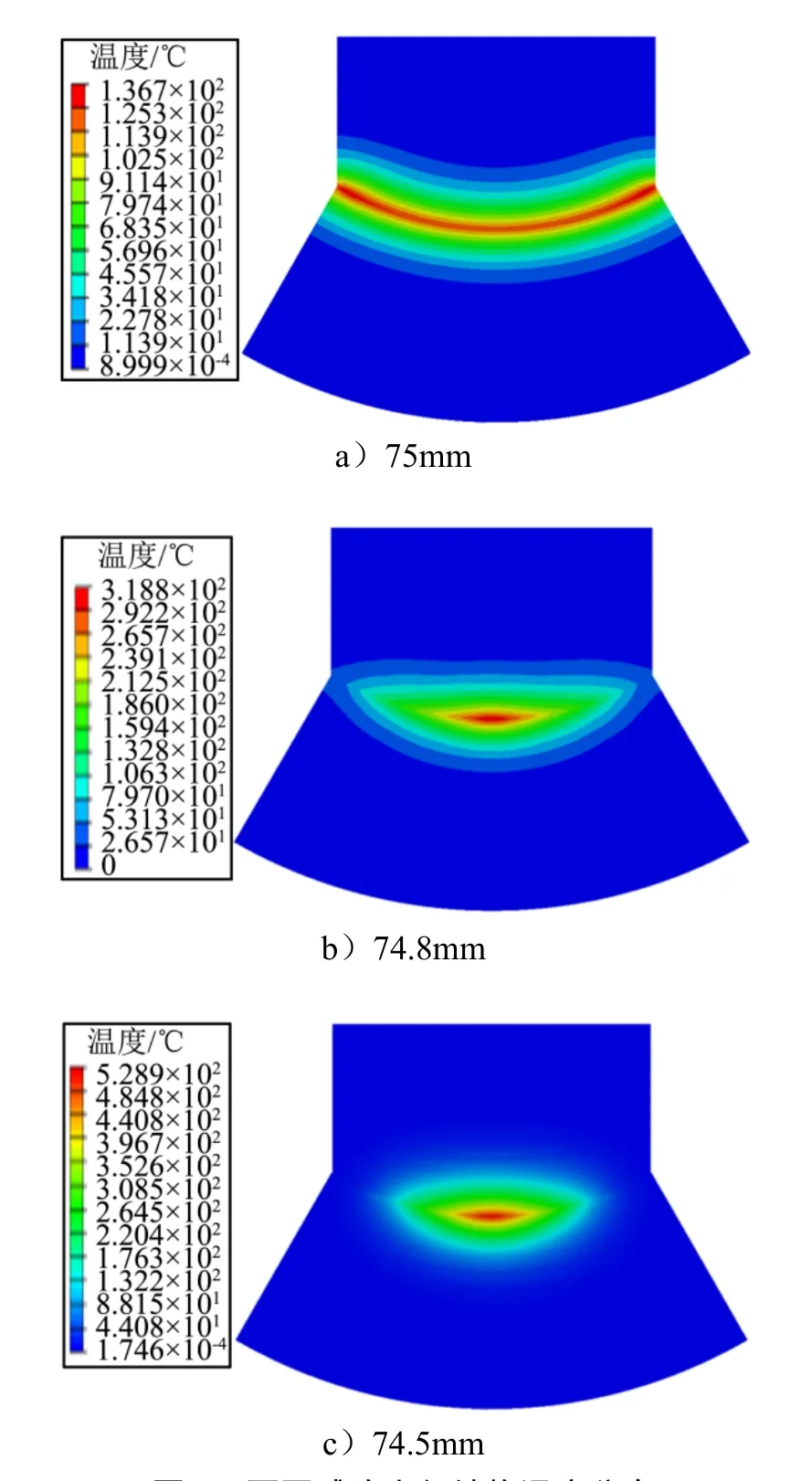
圖5 不同球頭半徑結構溫度分布Fig.5 Temperature Distribution of Structure with Different Ball Head Radii

4.3 轉動頻率對溫升的影響

針對不同的轉動頻率，通過仿真計算出了球頭半徑變化對結構最高溫度的影響規律，如圖6 所示。由圖6 可以看出，頻率越高，結構溫度越高，尤其在頻率較高的情況下，配合半徑對結構溫度影響更加顯著。

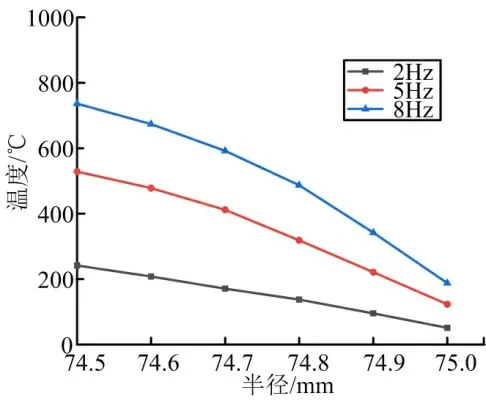
圖6 不同頻率下球頭半徑對溫升的影響Fig.6 The Influence of Ball Head Radius on Temperature Rise at Different Frequencies

4.4 接觸面摩擦系數影響分析

接觸面摩擦系數直接影響摩擦生熱總量及結構溫升，合適的摩擦系數是確保結構正常工作的必要條件。對摩擦系數的要求，直接影響接觸面潤滑方案的選擇。球頭-球窩標稱配合半徑的狀態下，通過仿真計算，獲取了不同摩擦系數狀態下，結構最高溫度的變化規律，見圖7。

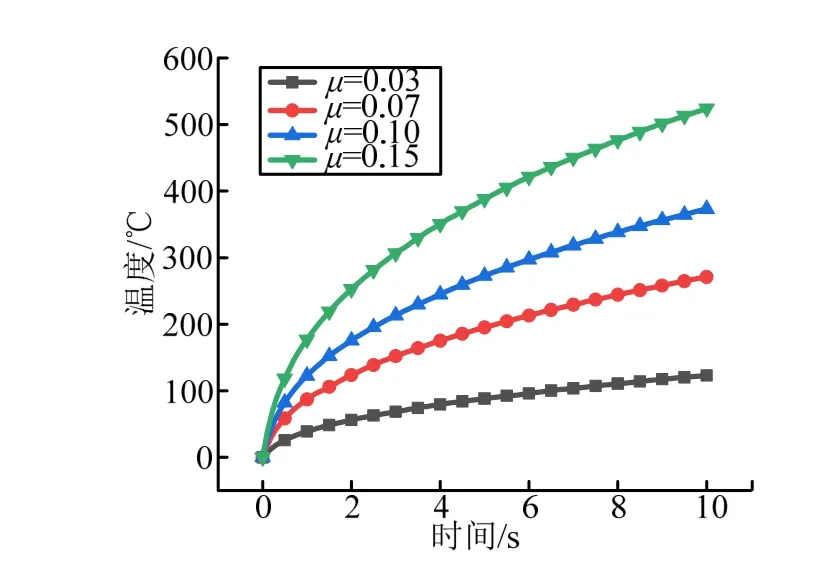
圖7 不同摩擦系數下的溫度隨時間變化Fig.7 The Temperature Changes with Time under Different Friction Coefficients

由圖7 可以看出，隨著摩擦系數的升高，結構溫度也在升高，摩擦系數為0.15 時，結構最高溫度達到了500 ℃，大幅降低了結構強度。若將溫度控制在150 ℃范圍內，則摩擦系數應不大于0.03。

4.5 轉動摩擦溫升對應力分布的影響

在球頭半徑為75 mm 時，由于集中載荷的作用，球窩結構發生了變形，應力集中在球窩邊緣處，為590 MPa。隨著球頭半徑減小，施加集中載荷后，最大應力點出現在球窩中心，在球頭半徑為74.9 mm 時，最大應力為645.2 MPa，隨著半徑的增加，球窩中心的應力逐漸增加。

由于結構應力是衡量結構承載能力的重要指標，通過仿真計算，給出了結構最高應力隨時間變化曲線，見圖8。由圖8 可以看出，球頭半徑為74.5 mm 和74.6 mm 時，結構最高應力隨時間增加而減小。這是因為球頭-球窩摩擦生熱導致結構溫度升高，改變了材料的強度特性，在球頭半徑為74.5 mm 時，由于結構溫升較快，且結構溫度較高，使得結構應力很快超出了屈服強度，進入了塑性區域，失去了承載能力。

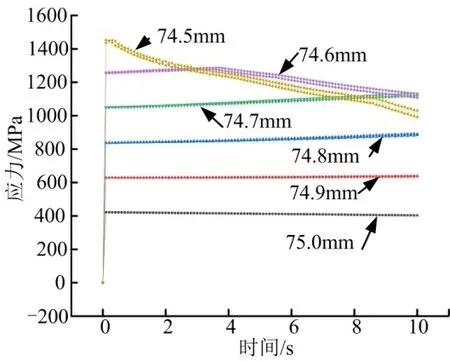
圖8 摩擦過程中應力的變化Fig.8 Stress Changes during Friction

5 三向載荷作用下結構強度分析

根據三向載荷值的特點可知，轉動摩擦生熱主要來源于軸向載荷的作用。對上述有限元計算模型，在下端施加隨時間變化的軸向載荷Fz，計算在2 種摩擦系數條件下（C01 狀態為摩擦系數0.15，C02 狀態為摩擦系數0.03），轉動摩擦時間為148 s 時，模型的最大溫度隨時間的變化情況，結果如圖9 所示。

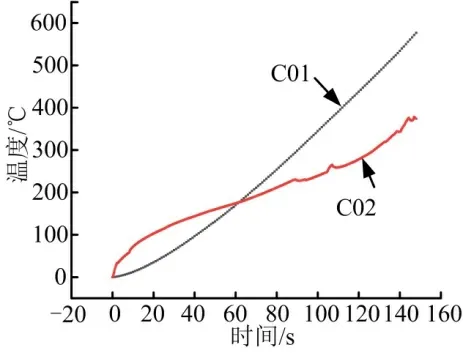
圖9 轉動摩擦生熱溫度變化Fig.9 Temperature Changes of Rotating Friction Heat

根據上述溫度的變化以及材料-溫度的模型，將C01 和C02 兩種狀態下轉動摩擦溫度變化導致的材料弱化等效為不同載荷下的材料參數，即材料強度參數會隨著載荷的變化而變化。計算結構在三向載荷作用下的應力分布如圖10 所示。

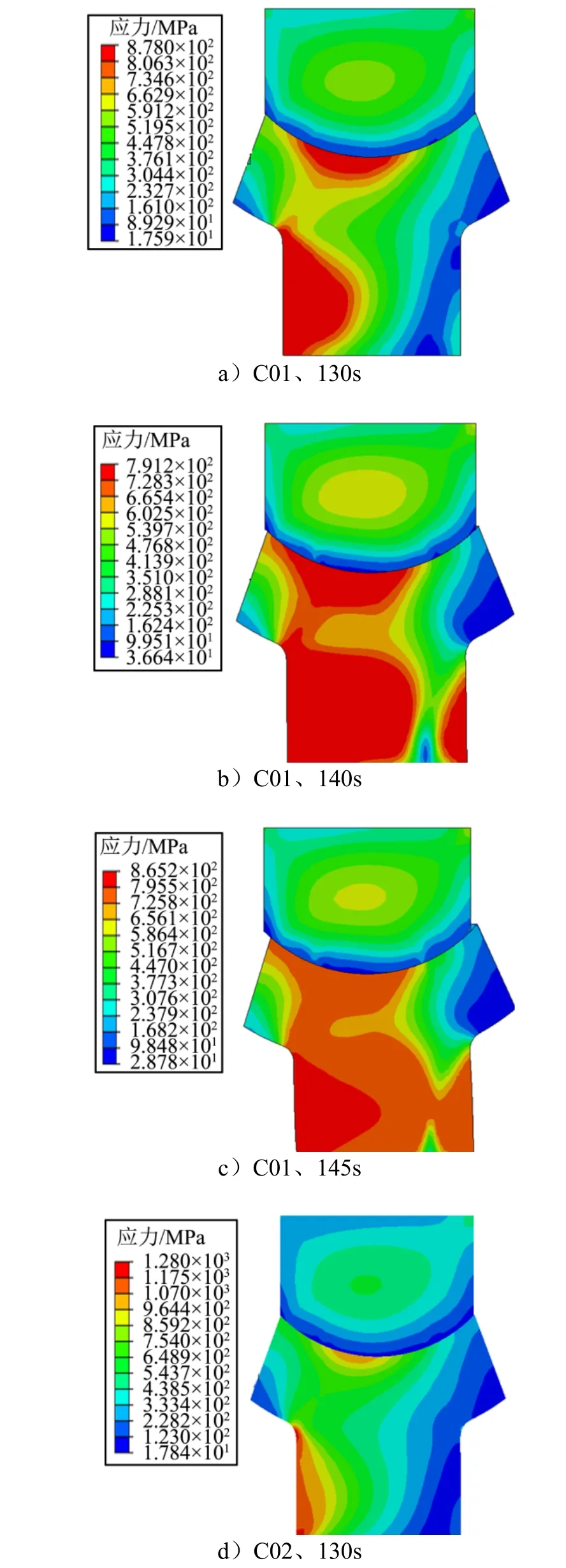
圖10 C01、C02 狀態下應力分布云圖Fig.10 Stress Distribution Nephogram in C01 and C02 State

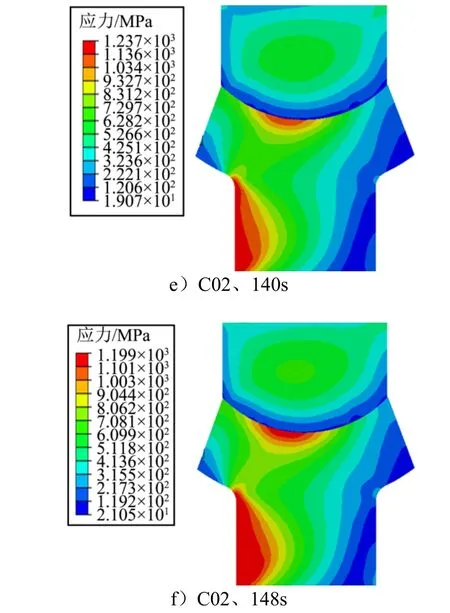
續圖10

根據圖10 的應力顯示結果，可以分析得到，在C01 狀態下，當連續變化的載荷增加到109 s，最大應力為1163 MPa，此后隨著時間的增加，溫度不斷升高，導致材料的力學參數發生變化，應力迅速減小，材料出現了嚴重的變形，當加載時間到達145 s，結構已經發生了嚴重的變形，此時計算已經不能收斂，說明結構已經完全失穩。在C02 狀態下，當連續變化的載荷增加到120 s 時，此時結構最大應力為1294 MPa，此后隨著時間的增加，應力減小。與C01 狀態相比，C02在加載時間到達148 s，捆綁結構仍能保持其穩定性。

圖11 顯示了球窩與球頭接觸位置的接觸壓力和材料強度隨加載時間變化曲線。

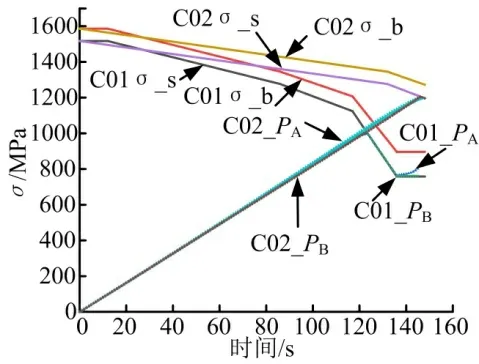
圖11 A 點和B 點的應力變化Fig.11 The Change in Stress at A and B

圖11 中A 點表示球窩一側，B 點表示球頭一側。在C01 狀態下，在0～123 s 內，A 點和B 點接觸壓力隨著連續載荷的加載時間增加而增加，在118 s 時材料強度隨著加載時間增加而迅速減少，當加載時間為145 s 時，結構完全失穩。在C02 狀態下，在0～146 s 內，A 點和B 點接觸壓力隨著連續載荷的加載時間增加而增加，雖然材料強度減小，但仍能保證結構的穩定性。在C01 狀態下，結構承載能力僅為總載荷值的84%。

6 結 論

本文對球頭-球窩配合的捆綁結構，建立求解接觸壓力和溫升變化的理論計算模型，并通過有限元數值仿真，分析了不同半徑差的球頭-球窩配合下，由于轉動摩擦生熱導致溫升變化，并與理論模型進行了對比。最后，對考慮轉動摩擦生熱的捆綁結構進行了強度分析研究。通過以上分析研究可以得到下述結論：

a）建立了能夠描述接觸壓力和溫升變化的理論模型，其中包含計算平均壓力的面積修正參數ε ，以及計算溫升變化時，用于修正溫升區域的等效材料質量參數α 和修正熱散失項的參數γ ；

b）球頭-球窩配合狀態對摩擦生熱和接觸面壓力影響較大，球頭與球窩半徑相差較大時，結構溫升較大，接觸面壓力較大，設計過程中，應嚴格控制球面配合尺寸；

c）接觸面摩擦系數對結構溫升影響較大，在沒有潤滑方案的情況下，結構溫升過大，因此，對于傳遞較大載荷的傳力機構，應選擇較好的潤滑方案，保證較低的摩擦系數，控制結構溫升。