基于邊長約束的凹域三角剖分求破片迎風面積

王佳穎,劉星雨

(1.武警工程大學 基礎部， 西安 710086；2.武警工程大學 裝備管理與保障學院， 西安 710086；3.上海交通大學海洋智能裝備與系統教育部實驗室, 上海 200240)

對于不規則形狀破片迎風面積(投影區域面積)的計算，通常采用二十面體均勻取向法的光學投影系統試驗[1]。該參數可進一步用于破片速度衰減分析、飛散特性研究以及比動能評估[3-7]。為便于自動化計算有限元破片迎風面積并提高求解精度，根據蒙特卡洛剖分投影法建立的平均迎風面積計算模型[8]提出一種最大邊長約束的凹域三角剖分算法。該算法以凸包Delaunay三角剖分算法為基礎[9-11]，以最大邊長約束為原則，對凹多邊形區域(簡稱凹域)邊界進行搜索重構，可進一步提高平均迎風面積計算模型的求解精度。目前基于最大邊長約束的凹域三角剖分自動化求解破片迎風面積方法，未見相關報道。雖然凸包Delaunay三角剖分算法也可直接用于破片迎風面積的計算，但對于形狀不可預知的自然破片而言其誤差仍有待進一步分析。

本文根據最大邊長約束的凹域三角剖分算法，通過凸包Delaunay三角剖分、剖分邊界凹凸性判別、最大邊長約束的剖分去除、剖分邊界邊搜索、邊界邊排序等步驟，得到任意形狀破片投影邊界并用于平均迎風面積模型計算。同時，驗證并對比了最大邊長約束的凹域三角剖分算法與凸包Delaunay三角剖分算法所得平均迎風面積的精度與求解時間。

1 有限元破片

本文以37 mm爆震彈為例[12]，模型采用1/4對稱建模，網格大小1 mm×1 mm×2 mm，殼體破碎情況如圖1(a)所示。在40 μs時刻殼體已破碎完全，將該時刻各破片單元節點數據導出進行投影剖分。為對比最大邊長約束的凹域三角剖分算法與凸包Delaunay三角剖分的迎風面積計算精度與效率，本文重點選擇頂部方向、徑向、底部方向形狀差異較大破片進行求解分析，其具體尺寸形狀如圖1(b)、圖1(c)、圖1(d)所示。

2 最大邊長約束的凹域三角剖分算法

2.1 算法概述

最大邊長約束的凹域三角剖分算法主要包括凸包Delaunay三角剖分、剖分邊界凹凸性判別、最大邊長約束的剖分去除、凹域邊界邊搜索、邊界邊排序5個步驟，其算法流程如圖2所示。

圖1 37 mm爆震彈破碎情況及不同方向上的有限元破片

圖2 最大邊長約束的凹域三角剖分算法流程框圖

凸包Delaunay三角剖分根據空外接圓規則可將離散投影節點集T構建成Delaunay三角網，并獲得凸包邊界dm及三角形矩陣dt_clist；剖分邊界凹凸性判別根據凸包三角剖分是否存在大于R的邊為原則進行遍歷，可提高破片投影為凸包時的計算效率；最大邊長約束的剖分去除以不大于凸包三角剖分平均邊長的λscale倍為原則，將超出約束邊長R的三角邊剔除；凹域邊界搜索根據公共邊、所有邊的差集運算，可得到邊界邊集合；邊界邊排序根據進棧、出棧的搜索遍歷，可得到經排序后的多邊形頂點。而后采用叉乘法對任意多邊形面積進行求解。

其中，T為無重復節點的投影點集；dm為凸包剖分邊界；dt_Clist為凸包三角剖分三角形節點編號；edges為凸包三角剖分升序排列的邊界；I為edges中不包含重復邊的行號集合；IN為edges的行號集合；IO為邊界邊行號；sort_vertices用于存放邊界頂點序列；polygon為按順(逆)時針排序的邊界邊節點坐標。

R取值定義如下：

(1)

其中，R為邊長約束值；λscale為放大因子；li為剖分三角形第i條邊的長度；ne為三角邊總數。根據凸包Delaunay剖分空外接圓準則及正六面體有限元節點距離特征，λscale取8～10時可較好地除去非凹域點集的三角邊，同時也可避免刪除凹域點集內剖分長度較大的有效三角邊。本文λscale取8。

2.2 凸包Delaunay三角剖分

當前隨機點集的Delaunay三角剖分方法主要有逐點插入法、分治算法、三角組網法等[11]。本文采用改進Bowyer-Watson逐點插入算法，該算法相比于Lawson算法計算效率更高；相比于標準Bowyer-Watson算法，魯棒性更好。改進的Bowyer-Watson算法通過引入放大因子，可避免標準超級三角形為大鈍角時外接圓心落在其外造成剖分邊界非凸包的情況。通過判定插入點在待剖分三角形右側、內側或外側位置，分別對剖分三角形進行入棧、再剖分、加入下次剖分等操作，最終可形成滿足空外接圓特性和最小角最大化特性的Delaunay三角剖分網格。其算法流程如圖3所示。

圖3 凸包Delaunay三角剖分算法流程框圖

判斷某點坐標(xi,yi)與三角形外接圓位置，可先根據三角形三頂點坐標(xi-1,yi-1)、(xi-2,yi-2)、(xi-3,yi-3)，求得外接圓圓心坐標(xo,yo)及半徑r，而后通過該點與圓心的距離以及與半徑之間的關系判定該點位置在圓內側、圓外側、圓右側。外接圓圓心坐標可根據圓上三點至圓心距離兩兩相等推導得到，表達式如式(2)、式(3)所示。點(xi,yi)與外接圓位置判定表達式如式(4)所示。

(2)

(3)

(4)

2.3 凹域邊界搜索排序及編程實現

凹域邊界搜索的差集運算表達式如式(5)：

EIO=EI-EIN-I

(5)

其中，EIO為凹多邊形區域邊界邊集合，有且僅有一條公共邊；EIN-I為凹多邊形區域的內部邊集合，存在兩個公共邊；EI為不包含重復邊的凹多邊形邊集合。

凹域邊界邊搜索與排序的代碼如下：

edges數據結構為一行存放一條角邊，連續三行為同一三角形；IA為edges中唯一值邊對應的行號；通過差集運算可獲得邊界邊點集并存入edges中；sort_vertices擬存放排序后的多邊形頂點序號，比當前edges行數多1，確保首尾頂點相連。最終經排序后的凹域邊界頂點坐標存入polygon中。

3 結果與討論

3.1 凹域剖分算法的可行性驗證

為驗證最大邊長約束的凹域三角剖分算法可行性，對圖1中的頂部破片、徑向破片及底部破片進行求解分析。經過一次投影、凸包三角剖分、帶最大邊長約束的凹域剖分結果分別如圖4(a)、(b)、(c)所示。從圖5可知三枚破片形狀尺寸差異較大，但通過最大邊長約束的凹域三角剖分算法均可得到破片投影圖形的邊界，并與投影點集吻合較好；凸包Delaunay三角剖分所得邊界比投影點集真實邊界面積更大。在單次投影結果中，圖4(a)中凸包剖分所得面積與凹域剖分面積相差不大，而在圖4(b)、(c)中與凹域剖分所得結果則相差較大。由此說明，相比于凸包Delaunay三角剖分算法，最大邊長約束的凹域三角剖分算法能更準確地對任意形狀破片投影邊界進行搜索，可進一步提高自然破片平均迎風面積的求解精度。

3.2 平均迎風面積精度對比

對比3枚破片5 000次投影后所得平均迎風面積結果，兩種算法下的迎風面積均值、標準差見表1。

圖4 不同方向破片的一次投影、凸包三角剖分、帶最大邊長約束的凹域剖分結果圖

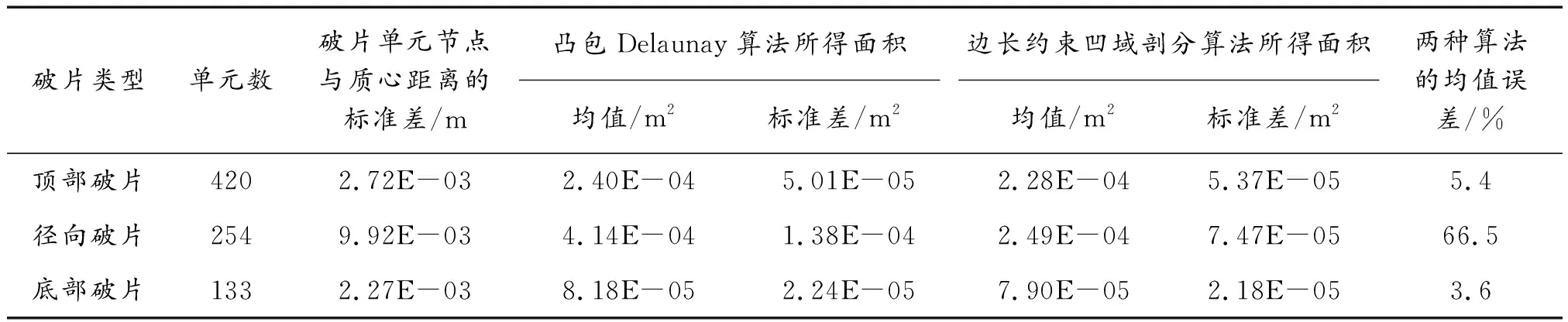
表1 凸包Delaunay算法與最大邊長約束的凹域剖分算法均值和標準差

從表1可知：凸包Delaunay算法頂部破片、底部破片標準差均比凹域剖分算法要小，但徑向破片標準差更大；凸包Delaunay算法不同方向破片所得迎風面積均值均比凹域剖分算法要大，其中頂部破片、底部破片均值誤差相差不大，僅為5.4%和3.6%的差異，但徑向破片均值誤差可達66.5%。分析造成凸包Delaunay算法各破片均值誤差差異較大的原因，主要由各破片形狀特征量單元節點與質心距離的標準差決定。對于節點與質心距離標準差較小的頂部、底部破片，其投影圖形更加緊湊，使得非凹域點集的無效三角邊更少，誤差相對變小；而對于距離標準差更大的徑向破片，其投影圖形更加狹長，使得非凹域點集的無效三角邊增多，進而誤差顯著增大。由此說明，凸包Delaunay算法的平均迎風面積精度受到破片形狀特征量影響較大，對于節點與質心距離標準差更小的破片而言凸包算法與凹域剖分算法精度相差較小，而對于節點與質心距離標準差較大的破片精度則相差較大。對自然破片的平均迎風面積求解，采用最大邊長約束的凹域剖分算法更能保證計算精度。

3.3 平均迎風面積求解時間對比

為避免CPU時鐘的誤差影響，選擇100次循環所得平均時間作為求解時間，兩種算法計算得到的時間見表2。運行環境為Intel (R) Core (TM) i7-8750h CPU @ 2.20 GHz，16 GB，Win10 x64。從表2可知：對于同一算法而言，不同方向的各破片求解時間相差不大，說明兩種算法的破片單元數對求解時間并不敏感；而對于同一破片而言，最大邊長約束的凹域剖分算法比凸包Delaunay剖分算法求解時間更長，約為30倍。若已知破片形狀為凸包或類凸包破片時，可優先選用凸包Delaunay剖分算法進行計算；而對于計算精度優先級高于時效的情況，則選用最大邊長約束的凹域剖分算法更為適合。

表2 凸包Delaunay算法與最大邊長約束的凹域剖分算法求解得到時間 s

4 結論

基于最大邊長約束的凹域三角剖分算法可對任意形狀破片的迎風面積進行求解。相比于凸包Delaunay算法，凹域三角剖分算法計算精度更高，但求解時間更長。在已知破片為凸包或類凸包形狀時，可優先采用凸包Delaunay算法進行求解。但對于形狀未知的有限元破片而言，采用凹域三角剖分算法更為適合。