獨立微網逆變器VSG控制慣量阻尼系數自適應研究

高明宇，劉金寧，馮長江

(陸軍工程大學石家莊校區 車輛與電氣工程系, 石家莊 050003)

隨著全球能源危機不斷加深，新能源技術日趨成熟，更加靈活、智能，可靠性更高的微電網系統受到越來越多的關注[1]。其中，新能源并網逆變器是連接新能源分布式電源與同步發電機的關鍵環節，其控制方法的選取對于系統的穩定性有著重要影響[2-3]。虛擬同步機控制方法(Virtual Synchronous Generator,VSG)能夠表現出發電機組的慣性特性和阻尼特性，得到廣泛應用[4]。不同于傳統發電機組，VSG控制中慣量和阻尼系數不受物理結構限制，取值更加靈活，具有更好的工程應用特性[5-6]。

針對VSG控制的慣量和阻尼參數優化控制，文獻[7-10]采用轉動慣量和阻尼系數自適應調節控制策略,能夠在負載變化時抑制系統頻率波動，從而提高穩定性，但以上研究主要針對單一逆變器輸出系統，沒有分析并聯系統，且只涉及頻率穩定，在功率調控方面沒有提及。文獻[11]針對雙機并聯系統，將負載變化的暫態過程分為兩個階段逐段分析，并提出一種基于虛擬電感和暫態阻尼的暫態主動功率分配優化方法，改進了暫態有功分配的動態性能，但是文獻中方法需要并聯微源的準確信息，且只改進了阻尼系數，對于慣量系數分析不足。文獻[12]提出了一種基于分布式通信架構的互阻尼控制策略，通過相鄰VSG間的互阻尼控制來抑制功率震蕩，但是這一控制方法引入通信線路和上級控制，增加了系統的復雜程度。文獻[13]利用等效同步發電機原理，提出了虛擬同步發電機多機并聯運行的虛擬慣量匹配方法，但文獻中只研究穩態功率分配問題，對于穩定性問題沒有涉及，同時也需要并聯微源的準確參數，自適應能力不強。

獨立微網運行時，各微源間功率波動和分配不均是影響穩定性的重要因素。對此，本文通過采集不同階段的系統功率波動差值和頻率變化率，采用微網慣量、阻尼系數自適應方法，逐步消除功率分配不均現象，并通過Matlab/Simulink進行仿真驗證。該方法不需要明確并網的發電機組各個參數值，具有較強的自適應能力。

1 慣量、阻尼系數特性分析

傳統VSG控制運動方程：

(1)

其中：Pm為虛擬原動機輸出的機械功率；Pe為輸出的電功率；J0為慣量系數；D0為阻尼系數；ω為轉子轉速；ω0為同步角速度[14]。

典型虛擬原動機的功頻表達式為式(2)：

Pm=Pn+Kω(ω0-ω)

(2)

其中：Pn為有功功率額定值；Kω為功頻調差系數。由式(1)可得：

(3)

J、D為慣性、阻尼分量，s為微分算子，與慣量、阻尼系數關系為式(4)：

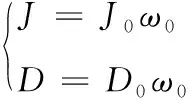
(4)

在穩態時，根據終值定理可得式(5)[15]：

(5)

傳統下垂控制的功頻特性方程為

ω=ω0+kp(Pn-P)

(6)

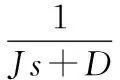
為進一步分析系統參數的影響，將分布式電源簡化建立并聯系統小信號模型如圖1所示[16]。

圖1 微源并聯系統模型結構示意圖

其中，其中E∠0為交流母線電壓，并設定相角為零，δi為VSG控制逆變器與發電機組的相角差，Ui∠δi(i=1,2)為各微源的逆變器輸出電壓值，Zl為并聯系統的公共負載，Zi(i=1,2)分別為逆變器和發電機組的輸出阻抗。

以圖2所示系統建立小信號模型。文獻[17]的方法，以功頻特性方程為基礎，建立系統的小信號模型：

(7)

s3+As2+Bs+C=0

(8)

其中：

(9)

結合式(7)、式(8)、式(9)，假設微源U1∠δ1為發電機組，其慣量系數、阻尼系數值恒為定值，U2∠δ2為VSG控制逆變器，通過改變參數值，系數根軌跡變化如圖2所示。

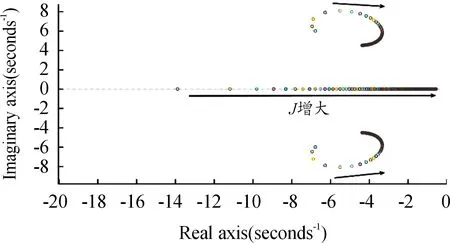
圖2 慣量系數根軌跡變化圖

(D1=D2=6，J1=1.2,J2=0～20)

由根軌跡圖3可知：當J1=J2=1.2時，系統為近似二階系統，特征根遠離虛軸，穩定性最佳，隨著參數值的繼續增大，系統逐漸由近似二階系統變為一階系統，特征根逐漸逼近虛軸，穩定性降低。同理可得當D1=D2=6時系統的穩定性最好，并隨著參數值增加，系統穩定性降低。因此當并聯系統的慣量、阻尼系數一致時，系統穩定性最佳。由于系統參數相同時，功率分配的暫態及穩態特性趨于一致，能夠減少功率環流及過沖，有利于系統穩定，這與參數小信號分析的結果一致。

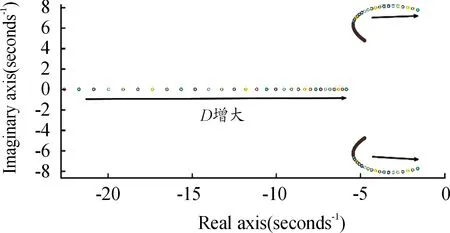
圖3 阻尼系數根軌跡變化圖

(J1=J2=1.2，D1=6,D2=0～50)

2 自適應慣量、阻尼控制原理

由式(1)可得：

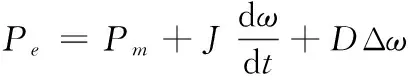
(10)

根據式(10)，設Pe1和Pe2分別為兩個微源的輸出功率，則有:

(11)

為簡化分析，設并聯微源的功頻下垂系數及容量一致，當系統并聯運行時，忽略線路阻抗，則有:

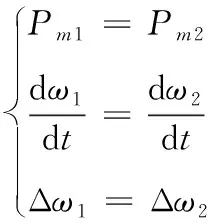
(12)

根據式(11)、式(12)，可知：

(13)

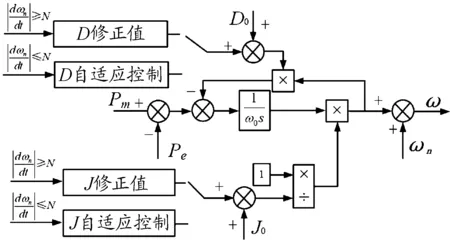
圖4 慣量阻尼自適應控制框圖

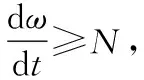
(14)

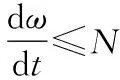
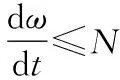
Pe1-Pe2≈(D1-D2)Δω

(15)

(16)

3 仿真驗證

將以上內容通過Simulink進行仿真。仿真參數如表1、表2所示。

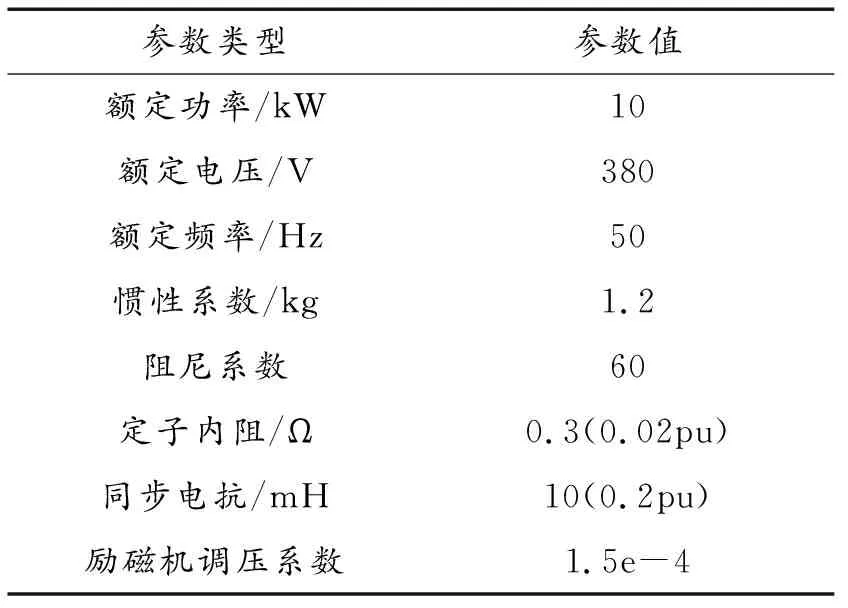
表1 發電機組參數

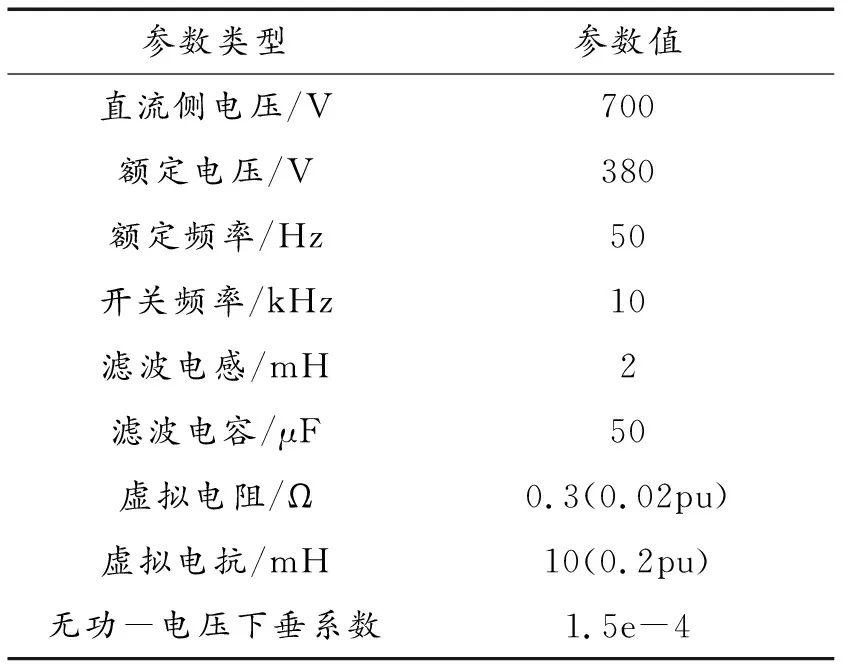
表2 逆變器控制參數

仿真以典型工況為例，區分并網和獨立運行兩種情況。并網運行中，預同步后在0.5 s切入大電網，1 s時加入5 kW負載，負載由2 s時切除負載并斷開并網開關。獨立運行時，并聯運行的工況設置如下：新能源逆變器帶8 kW負載運行，達到設置負載上限，空載啟動發電機組，在0.2 s時，打開預同步環節[18]，在0.5 s時打開并網開關，逆變器與發電機組并聯運行，1 s時加入5 kW負載，2 s時切除。3 s加入7 kW負載，4 s大負載切除，并聯開關斷開，新能源逆變器獨立帶7 kW負載繼續運行。其中逆變器分別采用下垂控制、VSG控制和自適應系數控制，觀察各微源有功功率輸出波動情況。

由圖5及數據分析可以看出，在并網運行時，系統的功率分配穩定有效。在獨立運行中，采用各控制方法輸出波形的數值對比如表3所示。如圖6所示，采用下垂控制時，系統調節速度較快，但是在負載功率波動時，微源的輸出功率不平衡。如圖7所示，采用定參數VSG時，系統功率波動較大，穩定時間長。如圖8所示。采用自適應慣量阻尼控制時，相較于定參數VSG控制，系統功率波動減小79%，穩定時間縮短31%，相較于下垂控制明顯消除功率波動偏差，且穩態偏差減小25%。由此可以看出自適應慣量阻尼控制具有一定的優越性。如圖9所示。系統完成自適應過程后，VSG控制的慣量和阻尼系數分別為J=1.17，D=6.16，與發電機組設定參數(J=1.2，D=6.08)相近。存在誤差的原因為系統的慣量阻尼系數存在一定的耦合，分段控制可以減少這一偏差，但是不能完全消除。

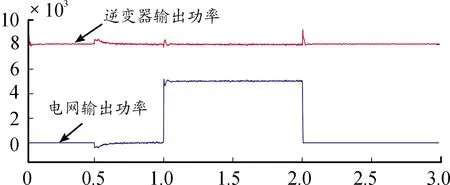
圖5 微網并網運行功率圖

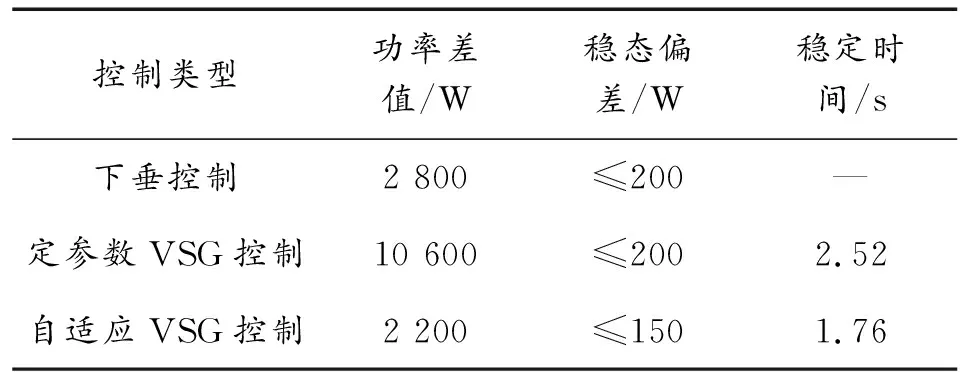
表3 控制輸出波形參數

圖6 下垂控制逆變器-發電機組并聯功率圖

圖7 固定慣量阻尼系數逆變器-發電機組并聯系統模型

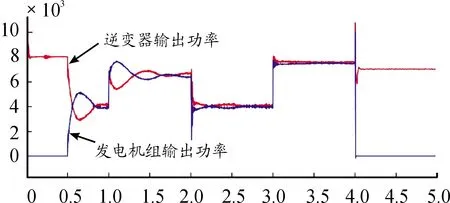
圖8 自適應慣量、阻尼系數控制逆變器-發電機并聯功率圖

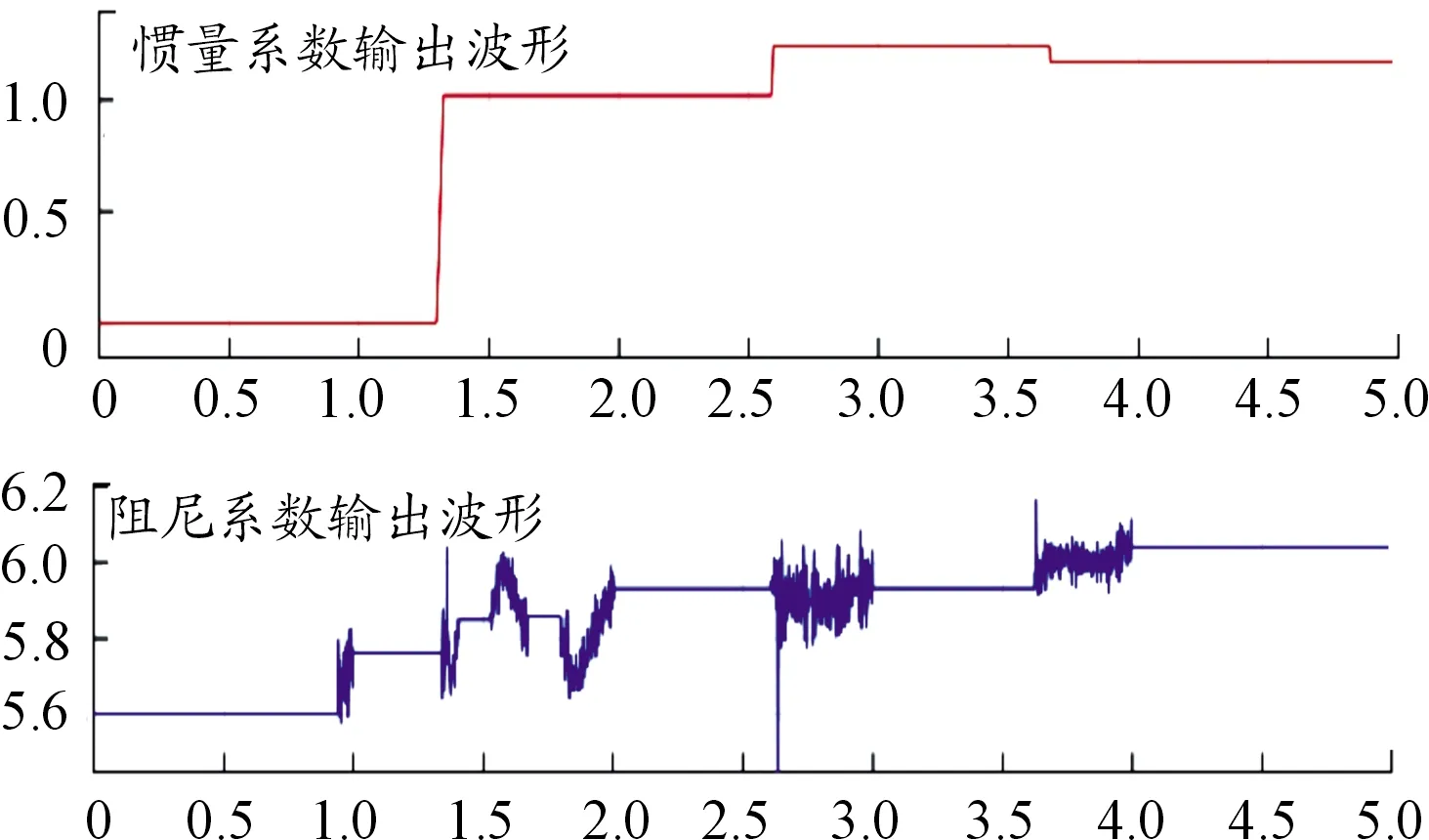
圖9 自適應慣量、阻尼系數輸出波形

4 結論

本文針對獨立微網中發電機組-逆變器雙機并聯系統的功率波動問題，提出了采用分段自適應慣量、阻尼控制方法，提升系統整體性能，并在Matlab/Simulink上對該方法進行了仿真實驗。結果表明：相較于傳統下垂控制并聯和固定參數并聯而言，該方法功率波動和穩態誤差更小，系統的穩定時間更短，該方法不需要明確發電機組的慣量和阻尼系數，能夠實現和任意機型的發電機組穩定并聯，克服了傳統并聯逆變器使用場景單一的缺陷，自適應性較強。