可公開驗證無證書的多接收者匿名簽密方案

陳 虹，朱亞囡，肖成龍，金海波，張子浩

遼寧工程技術大學 軟件學院，遼寧 葫蘆島125105

1 引言

公鑰加密和數字簽名往往需要很大的計算開銷，將兩者結合起來相較于獨立使用兩個算法，不僅能更快速的計算，而且消息擴展也更短，提高了效率，避免了資源浪費。1997年，Zheng[1]首次提出簽密的概念，簽密能夠在一個步驟內同時實現簽名和加密，其優越性吸引眾多研究人員關注，逐漸將簽密思想和現實的應用需求結合起來，提出很多具有特殊屬性的簽密方案[2-6]。為了滿足廣播環境下發送者同時發送消息給多個接收者的需求，2006年，李大興等[7]提出了一個發送者對應多個指定接收者的簽密方案，方案利用超奇異橢圓曲線上Tate對的特性，僅需一次加密，就能發送給多個接收者，提高了傳輸消息的效率，節省了資源。自此出現了很多多接收者簽密方案，然而方案生成的密文中往往包含發送者的身份或密文標記列表，致使多接收者簽密方案[8-13]密文泄露接收者的身份，為了解決接收者身份信息泄露的問題，2014 年，龐遼軍等[14]提出一種基于身份的多接收者匿名簽密方案，使用用戶的身份標識來生成公鑰，并將接收者的身份利用拉格朗日插值隱藏起來，使得解密時能夠驗證用戶身份的合法性，卻無法得到用戶的真實身份，且每個用戶可以驗證密文的有效性，保護了用戶的隱私，但該簽密方案私鑰是由密鑰生成中心（Key Generation Center，KGC）生成，面臨PKG 惡意泄露私鑰信息的情況，為了解決這一問題，研究人員提出了基于無證書體制的多個接收者的簽密方案，用戶和KGC 組合生成密鑰，因此KGC無法獲得用戶完整的私鑰，解決私鑰泄露的風險。2015年，于志敏等[15]提出一種基于多線性映射的多接收者簽密方案，在無證書體制下采用多個一級編碼相乘的方法，將方案的求解難度提升到了求解一個基于多級計算性Diffie-Hellman 問題，提高方案的安全性，但該公鑰尺寸大，且方案計算繁瑣，實用性不高。2016年，周彥偉等[16]提出一種無證書多接收者多消息簽密機制，該方案使用索引定位的方法標識密文，對接收到的密文需每個接收者各自定位到相應的密文，再去使用各自私鑰去解密，解密效率提高，但該方案操作復雜且容易暴露接收者的身份；2017 年，秦艷琳等[17]提出一種無雙線性對的無證書多接收者匿名簽密方案，該方案采用拉格朗日插值方法來隱藏接收者身份，且在簽密過程中沒有使用雙線性對，降低了計算開銷，然該方案被證明未真正實現接收者身份匿名性。

針對上述方案的不足，在隨機預言模型下提出一種可公開驗證的無證書多接收者匿名簽密方案，該方案解決了發送者身份模糊、接收者身份泄露的問題，且計算量適中，適合實際應用。本文首先介紹了方案的預備知識，然后提出了一種新的多接收者簽密方案，在隨機預言模型下證明了該方案的機密性、不可偽造性和可公開驗證性，最后與現有的一些多接收者簽密方案相比，證明本文方案所采用的方法更加的安全高效。

2 預備知識

2.1 雙線性映射

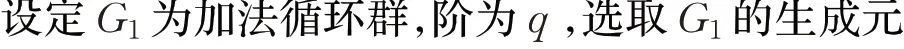
2.2 困難性問題

3 簽密方案

3.1 多接收者匿名簽密方案的構成

多接收者簽密由KGC、發送者和接收者三方構成，方案有以下幾個步驟。

（1）系統初始化算法：此算法是由KGC 來完成的，首先將系統的安全參數k 輸入進去，對應輸出主密鑰s 和參數params，其中主密鑰s 秘密保留，參數params公開。

（2）用戶密鑰生成算法：首先輸入參數params、主密鑰s 和用戶的身份ID，由KGC 輸出用戶的部分私鑰DID，用戶自己選取一個秘密值xID，將兩者結合起來生成完整的私鑰SKID，然后用戶輸入參數params 和身份ID，輸出用戶的部分公鑰，再由用戶秘密值和生成元計算出的值作為公鑰的另一部分，由此生成完整公鑰。

3.2 本文多接收者簽密方案的構成

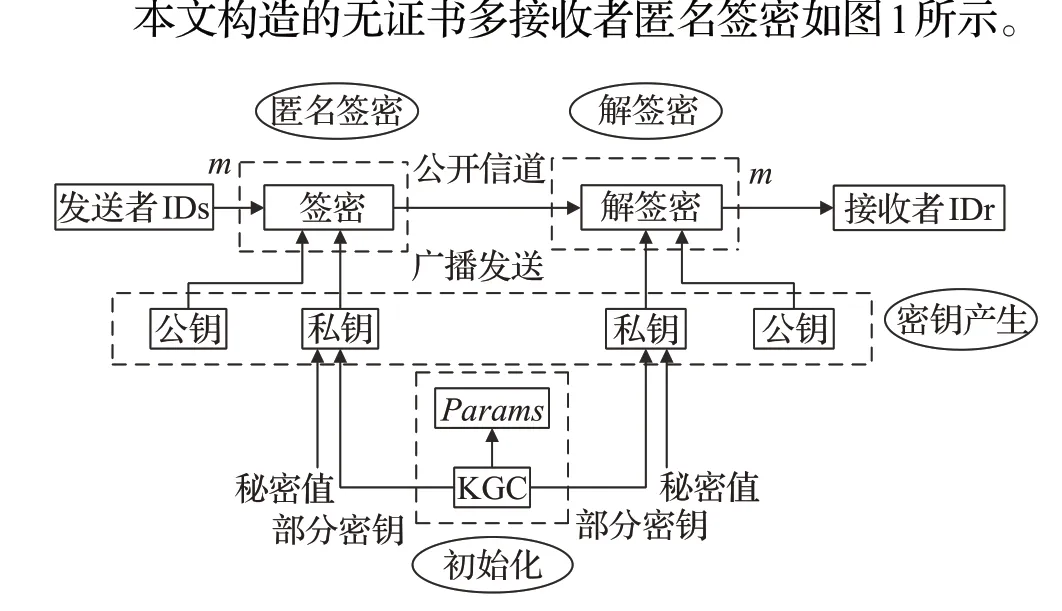
圖1 無證書多接收者匿名簽密方案

3.3 正確性證明

方案的正確性分析主要包括密鑰正確性、密文的可恢復性和發送者合法性、簽名正確性等分析，具體如下：

（1）密鑰正確性

用戶的密鑰由KGC 和用戶手中的部分密鑰組成，為了保證KGC 傳來的密鑰的可靠性，可以通過以下公式驗證KGC傳遞的部分私鑰的正確性：

4 安全模型

簽密的安全目標是對通信數據提供認證性和保密性。安全性可以根據敵手的不同，分為外部安全（只知道公共信息）和內部安全（合法用戶）。本章從機密性（選擇密文攻擊下的不可區分性，IND-CCA2）和認證性（選明文攻擊下不可偽造性，sUF-CMA）來定義內部安全性和外部安全性，通常可以通過KGC 和敵手之間的相互交互來驗證，參照文獻[13]的定義，利用四類游戲（游戲一、游戲二、游戲三、游戲四）來模擬方案受兩類敵手攻擊的過程，第一類敵手是惡意的用戶，可以無條件更換用戶的公鑰，但無法得知系統的主控鑰；第二類敵手是惡意的KGC，掌握著系統的主控鑰，但無法更換用戶的公鑰。兩類敵手和KGC中的算法之間的交互如圖2和圖3所示。

圖2 適應性選擇密文攻擊模擬圖

圖3 選擇消息攻擊模擬圖

4.1 機密性分析

4.2 不可偽造性分析

定義4（類型二攻擊下的不可偽造性）若在固定時間t內敵手SUF-CCA2 贏得游戲一優勢ε?是可以忽略不計的（執行qe次密鑰詢問，qs次簽密詢問，qd次解簽密詢問和q1,q2,q3,q4次對哈希函數H1,H2,H3,H4的詢問），則有算法B 能夠在t′≤t內，以優勢ε*≥ε?/2-qs/2k+1解決DL問題。

證明證明過程與定義3類似，此處不再論證。

5 性能分析

從計算效率和安全屬性上對方案進行分析，計算效率主要取決于多接收者匿名簽密和簽密驗證算法的計算量。因為散列函數和點加運算所用的時間遠小于其余的計算時間，可以忽略不計，因此計算量主要統計雙線性對、點乘和指數運算的執行次數，分別用E、P、M表示指數運算、雙線性對運算和點乘計算，一個雙線性對約等于20 個點乘，一個指數約等于3 個點乘，將本文方案和其他類似方案進行比較，結果如表1和表2所示。

表1 多接收者簽密計算效率

表2 多接收者簽密安全屬

從表1可以看出文獻[16]在計算開銷上存在明顯的優勢，但該方案使用的是索引定位的方法來確定接收者所屬的密文，需找到準確密文后再進行解密，操作復雜，且此段開銷并未計算進去；本文與文獻[15]相比，文獻[15]不使用雙線性對，計算開銷也較小，但隨著接收者增多，開銷增長的幅度相比本文也會加大；本文與文獻[17]相比，在隨著接收者增加的趨勢下有著相近的增長幅度。

從表2可以看出，文獻[14]、[16]和[17]相比，本文方案具有接收者匿名性，能解決接收者身份泄露的問題；本文與文獻[15]和[17]相比，能實現發送者身份匿名性，確保發送者身份不被泄露；本文與文獻[17]相比，本文具有可公開驗證性，能夠確保密文的有效性和發送者身份的合法性。本文方案與其他文獻相比安全性更高、更全，適用于網絡組播中的簽密服務、云中的數據共享以及網絡會議等領域。

6 結束語

針對多接收者簽密方案發送方和接收方身份泄露的問題，采用哈希函數和多項式將身份隱藏起來，保護了用戶的隱私，實現身份的匿名性，且方案可公開驗證密文有效性。然而方案在注重抗攻擊性能時，計算開銷就會有所忽略，因此平衡方案的運行效率和抗攻擊性能，仍是以后研究的重點。