指針網(wǎng)絡(luò)改進(jìn)遺傳算法求解旅行商問(wèn)題

陳思遠(yuǎn)，林丕源，黃沛杰

華南農(nóng)業(yè)大學(xué) 數(shù)學(xué)與信息學(xué)院，廣州510642

1 引言

遺傳算法屬于演化算法，是最優(yōu)化算法的一種。遺傳算法模擬自然界物種進(jìn)化，適者生存的規(guī)律，通過(guò)模擬物種進(jìn)化生成新種群過(guò)程中，基因交叉互換，變異等過(guò)程生成新的個(gè)體[1]。基因優(yōu)良的個(gè)體會(huì)被保留，延續(xù)至下一代，不斷改進(jìn)種群整體的基因。從理論上，隨著種群迭代，子代基因會(huì)優(yōu)于父代基因。然而，實(shí)際上并非如此，因?yàn)樽哟蚴芊N群基因質(zhì)量影響，質(zhì)量差的種群容易生成適應(yīng)度次的子代，會(huì)對(duì)算法的性能和尋優(yōu)速度造成影響[2]。這種影響可以通過(guò)對(duì)種群的擇優(yōu)構(gòu)造來(lái)避免。

遺傳算法在大規(guī)模最優(yōu)化問(wèn)題中，能取得最優(yōu)值或者次優(yōu)值。然而遺傳算法本身也存著諸多缺陷，在處理規(guī)模較大的最優(yōu)化問(wèn)題，如旅行商問(wèn)題（Traveling Salesman Problem，TSP），算法容易陷入局部最優(yōu)、收斂速度慢等問(wèn)題。遺傳算法相比精確算法，其求解過(guò)程是隨機(jī)性的，通過(guò)隨機(jī)的選中基因進(jìn)行互換和變異。交叉和變異算子是影響遺傳算法搜索過(guò)程的兩大重要因素[3]。目前，學(xué)者們?cè)诟倪M(jìn)遺傳算法搜索算子過(guò)程中提出了許方案，像自適應(yīng)遺傳算子[4]、改進(jìn)變異算子[5]等。

種群初始化是遺傳算法的第一個(gè)階段，也是影響遺傳算法性能的另一重要因素。初始種群影響著算法的收斂速度和算法的尋優(yōu)空間，是遺傳算法性能的決定因素之一[6]。傳統(tǒng)的遺傳算法常使用隨機(jī)策略生成初始種群集合，然而隨機(jī)初始策略帶來(lái)算法的不穩(wěn)定性，導(dǎo)致種群適應(yīng)度底下，搜索速度慢，容易陷入局部最優(yōu)等缺點(diǎn)，嚴(yán)重影響算法后期優(yōu)化搜索算子的應(yīng)用。如何優(yōu)化遺傳算法的初始種群階段，提供高質(zhì)量多樣性的種群個(gè)體是學(xué)者研究改善遺傳算法的方向之一。

本文提出一種基于指針網(wǎng)絡(luò)改進(jìn)遺傳算法初始種群模型，通過(guò)改進(jìn)指針網(wǎng)絡(luò)生成高適應(yīng)度種群，并結(jié)合基于漢明距離改進(jìn)輪盤(pán)賭策略對(duì)種群進(jìn)行改造，并將改進(jìn)模型應(yīng)用于求解旅行商問(wèn)題中。

2 基礎(chǔ)問(wèn)題的描述

2.1 TSP問(wèn)題

2.2 遺傳算法

遺傳算法通過(guò)模擬生物基因交叉變異等過(guò)程來(lái)生成目標(biāo)問(wèn)題新的解集，直到尋得最優(yōu)解。傳統(tǒng)遺傳算法主要求解步驟如下所示。

（1）種群初始化：初始種群的生產(chǎn)是遺傳算法的前備工作。初始種群產(chǎn)生許多解決方案，方案?jìng)€(gè)數(shù)取決于種群規(guī)模大小。初始種群的規(guī)模和質(zhì)量會(huì)對(duì)遺傳算法的搜索空間和搜索速度產(chǎn)生很大的影響。傳統(tǒng)遺傳算法主要使用隨機(jī)策略來(lái)生成種群來(lái)完成初始化，然而隨機(jī)算法帶來(lái)的不確定性會(huì)給遺傳算法搜索尋優(yōu)空間帶來(lái)很大影響。

（2）選擇最優(yōu)子代：遺傳算法模擬自然界優(yōu)勝劣汰的規(guī)則。對(duì)于當(dāng)下的存在的種群。算法會(huì)對(duì)大的種群進(jìn)行劃分N個(gè)子種群。在每個(gè)子種群中選取適應(yīng)度高的子代進(jìn)行保留，淘汰適應(yīng)度低的子代。以保證種群質(zhì)量。

（3）交叉和變異：交叉和變異算法是遺傳算法的種群的部分。交叉算子為遺傳算法帶來(lái)新的基因組合，擴(kuò)大搜索范圍。以一定概率Pc和Pm進(jìn)行交叉和變異操作。其中個(gè)體c的交叉概率為體c的適應(yīng)值，Pm亦然。

（4）重復(fù)（2）和（3）過(guò)程直至算法收斂。

遺傳算法雖然在求解城市規(guī)模較小的問(wèn)題時(shí)具有較快的尋優(yōu)速度，但在城市點(diǎn)集規(guī)模較大的TSP 問(wèn)題時(shí)，早熟、后期收斂慢等缺陷愈加明顯，影響算法性能[9]。其中，影響遺傳算法的主要因素為交叉變異概率和初始化種群。

2.3 指針網(wǎng)絡(luò)

指針網(wǎng)絡(luò)是由Vinyals 等人[10]提出的一種能從離散的輸入序列中學(xué)習(xí)到輸出序列條件概率的神經(jīng)網(wǎng)絡(luò)，它是sequence to sequence（簡(jiǎn)稱seq2seq）網(wǎng)絡(luò)模型的一個(gè)變種[11]，能有效用于學(xué)習(xí)到中低維度的組合優(yōu)化問(wèn)題，并能高準(zhǔn)確度預(yù)測(cè)出問(wèn)題的解。指針網(wǎng)絡(luò)的原理是將輸入映射為一系列按概率指向輸入序列元素的指針[10]，如圖1所示，xn和yn代表輸入網(wǎng)絡(luò)數(shù)據(jù)。

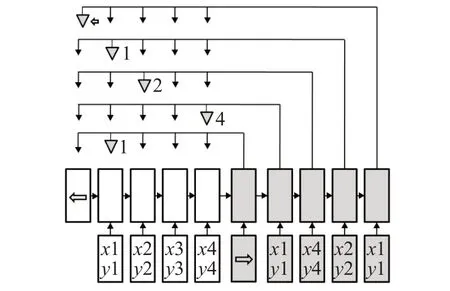
圖1 指針網(wǎng)絡(luò)模型

圖1中，白色的RNN用于處理輸入序列以產(chǎn)生編碼向量，其中編碼向量用于使用概率連規(guī)則生成輸出序列和另一個(gè)灰色的RNN。指針網(wǎng)絡(luò)在原本的seq2seq模型的基礎(chǔ)上的修改，并不是通過(guò)加權(quán)所有的結(jié)果得到輸出，而是直接將softmax的結(jié)果值作為輸出的條件概率，可以用公式表示為：

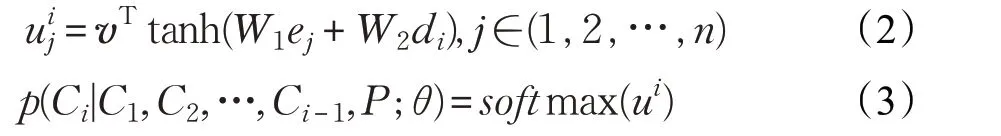
其中v和W1、W2是模型可訓(xùn)練的參數(shù)，向量uij為輸入元素的指針，softmax 將uij歸一化為輸入序列在輸出元素中的分布。p(Ci|C1,C2,…,Ci-1,P;θ)則代表從輸入元素被選中作為輸出元素的條件概率。

2.4 種群初始化改進(jìn)方案

傳統(tǒng)遺傳算法在種群初始化中，一般使用隨機(jī)策略。而隨機(jī)策略自身存在諸多缺陷，如種群個(gè)體質(zhì)量偏低、無(wú)法保證種群多樣性等，這也導(dǎo)致傳統(tǒng)遺傳算法會(huì)出現(xiàn)早熟陷入局部最優(yōu)等缺陷。近年來(lái)，學(xué)者們從各種組合優(yōu)化方案中探討對(duì)初始種群的優(yōu)化改進(jìn)，有以下幾種主流改進(jìn)方案。

2.4.1 近領(lǐng)域搜索策略

近領(lǐng)域搜索，也叫最鄰近初始化（Nearest Neighbor，NN）[12]，是貪婪初始化（Greedy）的一種。NN 從隨機(jī)城市出發(fā)，每次都從剩余城市中選擇與當(dāng)前所在城市距離最近的城市作為下一個(gè)城市，重復(fù)過(guò)程直到走完范圍內(nèi)所有城市。可用公式表示為：

其中Tt為當(dāng)前路徑長(zhǎng)度，Dcicr表示當(dāng)前城市Ci與剩余城市集合Cr之間的距離。

2.4.2K-means搜索策略

K-means是基于K中心點(diǎn)聚類的初始化方案[13]，算法過(guò)程可描述為，在有n個(gè)觀測(cè)點(diǎn)集中尋找K個(gè)中心點(diǎn)，最小化觀測(cè)點(diǎn)與其最近中心點(diǎn)的平均距離。其具體步驟如下：

（1）基于K-means 聚類將N個(gè)城市集合分成K組，其中，

（2）GA 初始化過(guò)程中，從K組聚類中心集合中獲得局部最優(yōu)子路徑，再將K個(gè)局部最優(yōu)子路徑整合為全局最優(yōu)路徑。

（3）將上一步驟獲得的最優(yōu)路徑里面的局部最優(yōu)子路徑斷開(kāi)，首尾交換，并記錄新路徑的長(zhǎng)度。如果行路徑大于當(dāng)前最優(yōu)路徑，則替換當(dāng)最優(yōu)路徑。

（4）重復(fù)（3），直到所有子路徑交換完成，則完成K-means初始化步驟。

2.4.3 線性規(guī)劃策略

線性回歸初始化是一種基于線性回歸（Linear Regression，LR）[14]，將TSP城市劃分為幾個(gè)子區(qū)域，然后，在子區(qū)域中，反復(fù)迭代求使得子區(qū)域路徑最短，最后合并得到初始化路徑集合的過(guò)程。算法的思想基于回歸和連續(xù)分區(qū)，通過(guò)把大問(wèn)題轉(zhuǎn)化為局部最優(yōu)問(wèn)題。設(shè)LR 平面劃分線為y=a+bx，其中，x是解釋性或者獨(dú)立變量，y是非獨(dú)立變量a和b是代表線性域的常量，其中：

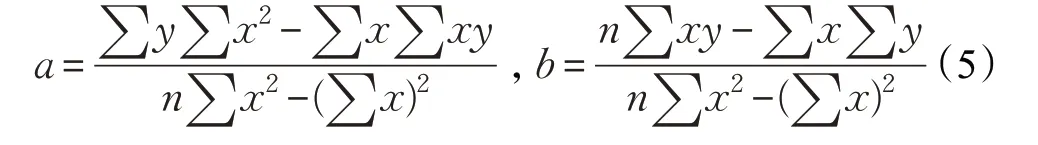
LR的求解方式類似于K-means，都是基于一定的基線將初始種群進(jìn)行劃分成小的區(qū)域模塊，再在小區(qū)域中進(jìn)行局部求解。其缺點(diǎn)也和K-means 一樣，受到LR 回歸劃分的影響大，容易陷入局部最優(yōu)等。

3 指針網(wǎng)絡(luò)改進(jìn)初始種群模型

本文引入深度學(xué)習(xí)網(wǎng)絡(luò)——指針網(wǎng)絡(luò)來(lái)優(yōu)化初始種群的構(gòu)造。指針網(wǎng)絡(luò)是基于seq2seq 網(wǎng)絡(luò)模型改造，能準(zhǔn)確學(xué)習(xí)到組合優(yōu)化問(wèn)題的組合規(guī)則，在TSP 問(wèn)題中，指針網(wǎng)絡(luò)能在中低規(guī)模的TSP模擬數(shù)據(jù)中獲得高準(zhǔn)確度結(jié)果。本文提出基于指針網(wǎng)絡(luò)的遺傳算法初始化方案，以此改善遺傳算法的初始種群構(gòu)造，提高整體算法性能。

3.1 指針網(wǎng)絡(luò)改進(jìn)遺傳算法流程

初始種群的本文引入基于指針網(wǎng)絡(luò)改進(jìn)遺傳算法模型，即PNGA。模型通過(guò)指針網(wǎng)絡(luò)來(lái)改進(jìn)初始種群總體質(zhì)量，并以改進(jìn)優(yōu)化策略組合優(yōu)化新種群結(jié)構(gòu)，保證種群的質(zhì)量與多樣性。

PNGA模型具體流程步驟如下所示：

（1）基于指針網(wǎng)絡(luò)生成高質(zhì)量初始種群。

（2）將指針網(wǎng)絡(luò)初始種群與隨機(jī)初始種群以最優(yōu)個(gè)體保留策略保留雙方優(yōu)良個(gè)體，形成新初始種群。

（3）將（2）中剩余個(gè)體，以基于漢明距離改進(jìn)輪盤(pán)賭策略，加入到新種群中。

（4）結(jié)合自適應(yīng)遺傳算子，提高算法迭代效率。

PNGA模型的流程圖如圖2所示。

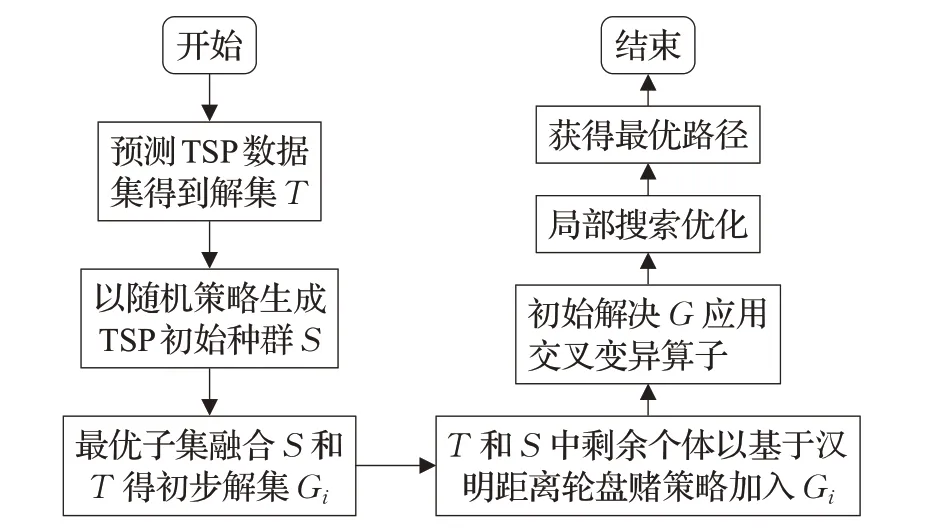
圖2 PNGA流程圖

3.2 改進(jìn)初始種群構(gòu)造策略

種群整體素質(zhì)不僅受個(gè)體質(zhì)量影響，還取決于種群整體個(gè)體的基因多樣性組成。在保證種群有高質(zhì)量個(gè)體的同時(shí)，為了優(yōu)化種群個(gè)體組成，PNGA 模型以兩種構(gòu)造方案相結(jié)合。

設(shè)GA 種群規(guī)模上限為Psize，GA 隨機(jī)初始化得到種群為S，指針網(wǎng)絡(luò)解集為T(mén)，目標(biāo)初始種群為G。為了優(yōu)化目標(biāo)種群G質(zhì)量與多樣性，模型使用的兩種構(gòu)造策略如下。

3.2.1 最優(yōu)子代融合策略

（1）首先，生成Psize大小的初始種群S和指針網(wǎng)絡(luò)解集T。

（2）對(duì)S和T分別計(jì)算集合中個(gè)體的適應(yīng)度。

（3）對(duì)S和T分別取適應(yīng)度高的子集加入新解集G，以Sg和Tg表示。為了最大程度保留指針網(wǎng)絡(luò)解集T中個(gè)體的優(yōu)勢(shì)，本文將和以特定比例加入，則新種群G的初步集合Gi組成如下：

3.2.2 基于漢明距離輪盤(pán)賭策略

在有優(yōu)秀個(gè)體的情況下，為了優(yōu)化種群多樣性。本文提出一種基于漢明距離的輪盤(pán)賭策略。

漢明距離是一種測(cè)量個(gè)體差異的方法，在信息學(xué)中，它表示兩個(gè)長(zhǎng)度相等的字符串中，對(duì)應(yīng)位置中不相同的個(gè)數(shù)[15]。以TSP 序列為例，TSP 序列a=[0，1，4，2，3，0]和b=[0，1，2，3，4，0]之間的漢明距離為3，因?yàn)樾蛄衋和b中第3、4、5位不相同。假設(shè)個(gè)體C2和C2的漢明距離為ρH(C1,C2)。

種群個(gè)體之間的漢明距離是種群多樣性的度量之一。為了計(jì)算種群之間的多樣性，必須計(jì)算出種群中每個(gè)個(gè)體之間的漢明距離。假設(shè)大小為N的初始種群，則種群平均漢明距離DH可以表示為：

4 仿真實(shí)驗(yàn)及分析

為驗(yàn)證PNGA初始化模型的有效性，實(shí)驗(yàn)主要從兩方面進(jìn)行比較：第一部分主要對(duì)比PNGA改進(jìn)模型和主流初始化方案的在隨機(jī)數(shù)據(jù)集和TSPLIB 上的效果對(duì)比；第二部分主要對(duì)比PNGA與主流啟發(fā)式算法的求解準(zhǔn)確度差異。實(shí)驗(yàn)數(shù)據(jù)采用隨機(jī)模擬數(shù)據(jù)和TSPLIB上基于歐幾里德距離的對(duì)稱TSP城市數(shù)據(jù)。

4.1 實(shí)驗(yàn)設(shè)置

實(shí)驗(yàn)采用python 語(yǔ)言和tensorflow 框架，在Linux，內(nèi)存8 GB，CPU 為i7-6700 環(huán)境下運(yùn)行。指針網(wǎng)絡(luò)訓(xùn)練集采用了隨機(jī)生成策略，以[0，1]×[0，1]范圍內(nèi)生成的隨機(jī)數(shù)據(jù)作為城市坐標(biāo)，城市數(shù)量為20～100 之間隨機(jī)生成。并用谷歌優(yōu)化器（google optimization tools，or-tools）求解作為訓(xùn)練標(biāo)簽。GA 算法的初始種群大小為64。優(yōu)化算子2-opt和片段交換swap次數(shù)為5。

4.2 PNGA與主流改進(jìn)方案種群初始化系數(shù)對(duì)比

種群路徑圖是展示初始化路徑質(zhì)量最為直觀的衡量方法之一，優(yōu)秀的初始化路徑圖具有點(diǎn)與點(diǎn)之間連接緊湊，交叉路徑少，路徑間最長(zhǎng)距離短等特點(diǎn)。為了和PNGA 進(jìn)行對(duì)比，選取了研究進(jìn)展中的NN、K-means、LR進(jìn)行對(duì)比，具體對(duì)比實(shí)驗(yàn)如下所示。

4.2.1 初始種群質(zhì)量比較

本節(jié)主要從初始種群的結(jié)果對(duì)比和初始種群的質(zhì)量對(duì)比討論不同初始化方案的優(yōu)劣性。

種群路徑圖是展示初始化路徑質(zhì)量最為直觀的衡量方法之一，優(yōu)秀的初始化路徑圖具有點(diǎn)與點(diǎn)之間連接緊湊，交叉路徑少，路徑間最長(zhǎng)距離短等特點(diǎn)。為了和PNGA 進(jìn)行對(duì)比，本節(jié)選取了研究進(jìn)展中的NN[12]、K-means[13]、LR[14]進(jìn)行對(duì)比，初始化路徑圖如圖3所示。

圖3 為在50 個(gè)城市規(guī)模下，4 種不同初始化方案的初始化路徑對(duì)比圖。從圖中可以直觀的看出，NN 的路徑構(gòu)成上，交叉點(diǎn)較多，長(zhǎng)距離點(diǎn)存在，路徑構(gòu)成較為不規(guī)則，初始化路徑的總體效果較差；K-means 相比NN，路徑圖中，交錯(cuò)點(diǎn)較少，但仍然存在部分交錯(cuò)。長(zhǎng)距離點(diǎn)較少，因?yàn)榻徊娲嬖谝矊?dǎo)致長(zhǎng)路徑明顯。總體路徑初始化效果優(yōu)于NN。LR 在路徑圖構(gòu)成上和K-means 類似，交錯(cuò)點(diǎn)少，長(zhǎng)距離路徑少，初始化路徑效果和K-means 相當(dāng)。PNGA 相比K-means 和LR，具有更少的交叉點(diǎn)，長(zhǎng)距離也明顯少于K-means和LR，總體初始化效果位于最優(yōu)。從圖中分析，可以看出，PNGA 在n=50這樣的中低規(guī)模城市路徑中的初始化效果略優(yōu)于K-means 和LR，總體上遠(yuǎn)超NN，從初始化圖直觀效果上，處于初始化方案中效果最好的一個(gè)。

除了初始化路徑構(gòu)成比較外，實(shí)驗(yàn)還從種群的多樣性和平均個(gè)體值方面進(jìn)行驗(yàn)證。本文實(shí)驗(yàn)與研究進(jìn)展方法在平均路徑和種群多樣性上進(jìn)行對(duì)比驗(yàn)證。其中，參數(shù)AVGR代表在城市大小n恒定下，算法的平均初始化路徑均值，AVGR 越小，證明種群的平均個(gè)體質(zhì)量越高，獲得的路徑越短，初始種群質(zhì)量越高。CH代表種群個(gè)體的平均漢明距離均值，漢明距離是衡量集合中個(gè)體差異值的有效方法之一，CH越大，代表種群中個(gè)體間的差異大，種群多樣性更加豐富，能降低算法迭代過(guò)程中陷入局部最優(yōu)的概率。實(shí)驗(yàn)記錄PNGA 對(duì)比NN 和K-means 和LR，在20～100 個(gè)點(diǎn)TSP 模擬數(shù)據(jù)上進(jìn)行種群初始化的結(jié)果，分別計(jì)算各自初始種群的CH 值和AVGR值，如表1所示。

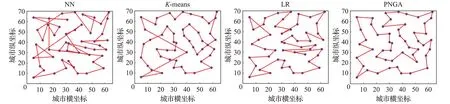
圖3 4種方案初始路徑圖對(duì)比

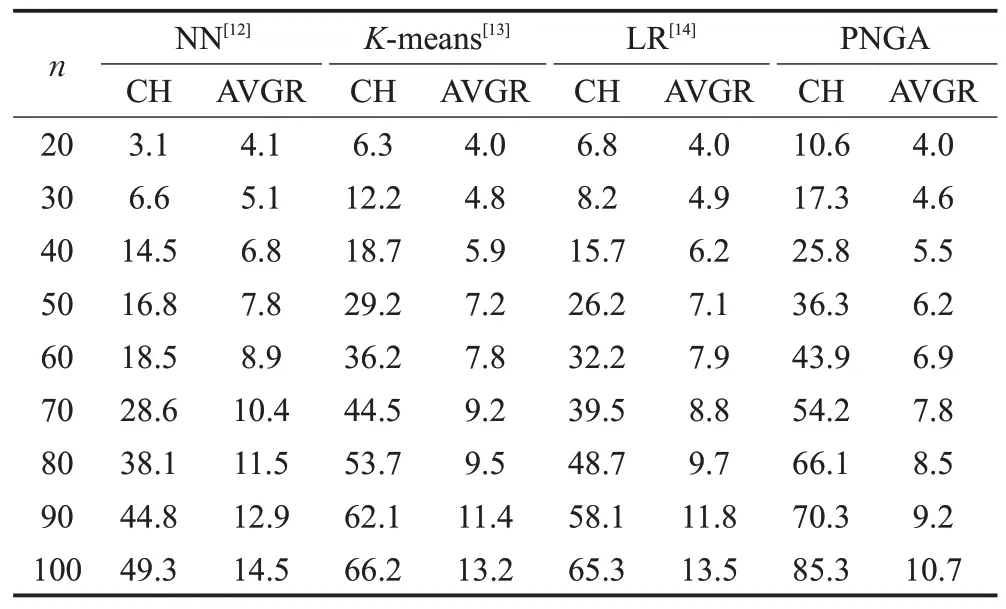
表1 不同方案的初始種群比較

從CH 方面看，NN 的平均CH 值均比其他方法要低，NN 的初始化是基于貪婪策略而來(lái)的，這也導(dǎo)致了NN 初始化過(guò)程中種群的多樣性低，容易陷入局部最優(yōu)而無(wú)法進(jìn)行全面搜索。K-means的CH相比LR，略次于LR。K-means 受限于K中心點(diǎn)的選取，在種群組成上無(wú)法構(gòu)成很多樣性豐富的初始種群。PNGA模型的CH優(yōu)于LR 和K-means，在種群多樣性上，PNGA 的種群多樣性與其他算法對(duì)比均有絕對(duì)優(yōu)勢(shì)。

4.2.2 TSPLIB實(shí)例比較

基于表1 初始種群質(zhì)量對(duì)比，PNGA 和K-means[13]、LR[14]3 種初始化模型在TSPLIB 實(shí)例上進(jìn)行對(duì)比，詳見(jiàn)表2（表格中路徑值均經(jīng)過(guò)四舍五入取整處理）。其中，“BKS”表示TSPLIB 實(shí)例數(shù)據(jù)已知最優(yōu)解（Best Known Solution）。對(duì)PNGA 和K-means、LR 分別進(jìn)行了50 次求解，算法內(nèi)部最大迭代次數(shù)為100。“迭代次數(shù)”表示算法內(nèi)部收斂所需迭代次數(shù)。實(shí)驗(yàn)記錄算法所得解的“最優(yōu)值”和“最差值”、50 次平均值“AVG”，并計(jì)算對(duì)應(yīng)PD值。PD值的計(jì)算公式如下：

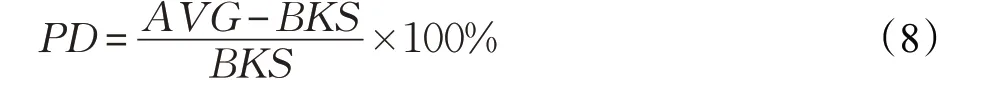
如表2，是K-means 和PNGA 算法在各項(xiàng)系數(shù)上的比較。在有優(yōu)勢(shì)種群的環(huán)境下，對(duì)表1中數(shù)據(jù)進(jìn)行分析比較，在迭代速度上，PNGA 相比K-means 模型，迭代次數(shù)上同比減少了15%左右的時(shí)間，相比LR，同比減少了10%的迭代時(shí)間。

最優(yōu)值方面，PNGA 在最優(yōu)值方面接近BKS，在最短路徑方法面，PNGA在規(guī)模較小的TSPLIB數(shù)據(jù)集上，均能取得最優(yōu)值，在規(guī)模較大的數(shù)據(jù)中，PNGA 能部分接近最優(yōu)，相比K-means，在不同規(guī)模數(shù)據(jù)集上，大約提升5%～15%左右，相比同等時(shí)間內(nèi)，K-means 和LR 求解上和BKS相比，均有不小的誤差，其中，LR在BKS上的誤差相比K-means 的誤差大3%左右。此外，在最差值Worst 上，K-means 的最差值相比LR 和PNGA 高了5%～10%左右，絕對(duì)誤差上比較大。PNGA最差值波動(dòng)上優(yōu)于LR，最優(yōu)值和最差值之差反饋于PD值。

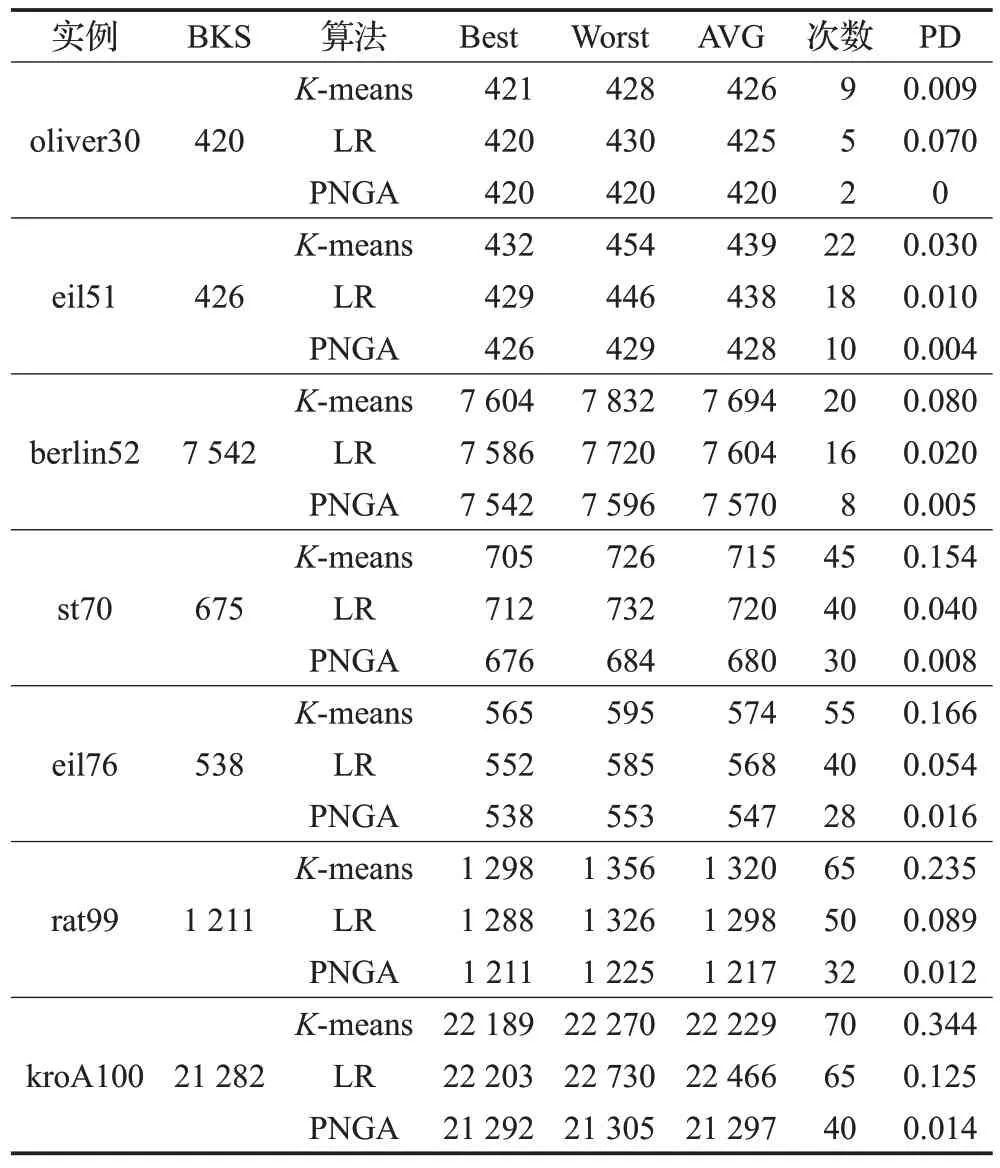
表2 PNGA與K-means、LR在TSPLIB的實(shí)例比較

在方差PD值上，PNGA的PD值波動(dòng)總體上較為平穩(wěn)，隨著城市規(guī)模n的不斷增大，PNGA、K-means、LR均有較大的上升波動(dòng)，PNGA 的PD 值波動(dòng)和LR 較為接近，K-means 算法的PD 值波動(dòng)較大，這和K-means 自身聚類中心點(diǎn)有關(guān)，會(huì)引起K-means 算法的不穩(wěn)定性，相比基于深度學(xué)習(xí)改進(jìn)的PNGA模型在求解過(guò)程中的PD值波動(dòng)小，算法更加穩(wěn)定。

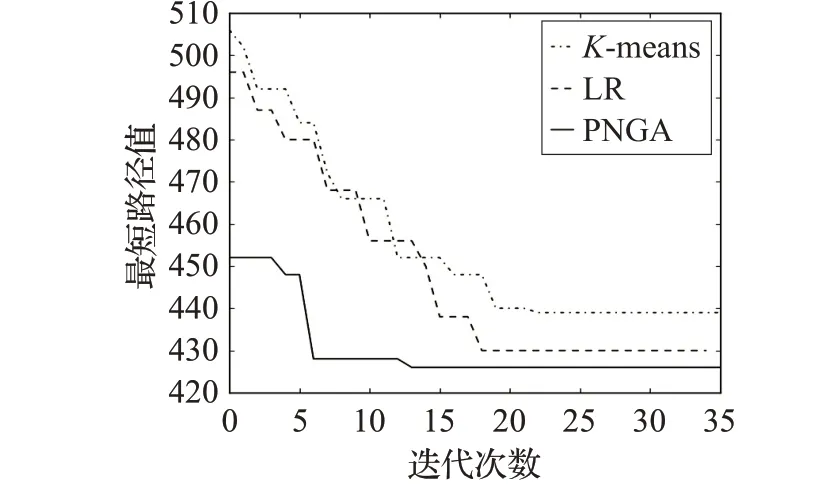
圖4 eil51算法收斂曲線對(duì)比

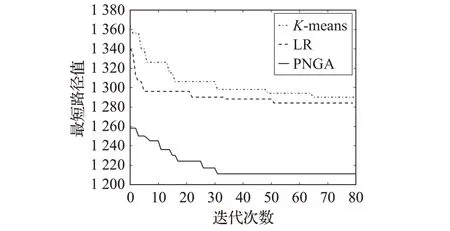
圖5 rat99算法收斂曲線對(duì)比

如圖4 和圖5 分別為3 種算法在實(shí)例eil51 和rat99上的收斂曲線對(duì)比圖。從圖中可得，在不同規(guī)模的實(shí)例中，PNGA 的初始路徑值明顯優(yōu)于K-means 和LR，PNGA 初始種群適應(yīng)度相比其他算法更高。從總體的收斂速度上PNGA＞LR＞K-means，PNGA收斂速度更快，所需迭代次數(shù)更少，反映出PNGA 算法的尋優(yōu)能力更強(qiáng)。從收斂曲線中分析可知，本文提出PNGA算法具有更好的尋優(yōu)能力和尋優(yōu)速度。

4.2.3 PNGA與主流啟發(fā)式算法比較

為了進(jìn)一步研究PNGA 模型性能。本文將PNGA和研究進(jìn)展中的主流啟發(fā)式算法在最優(yōu)路值上進(jìn)行了對(duì)比，如表3所示，其中SA-MMAS[19]和SOS-SA[17]是基于模擬退火算法，IMRGHPSO[18]是基于粒子群算法PSO。

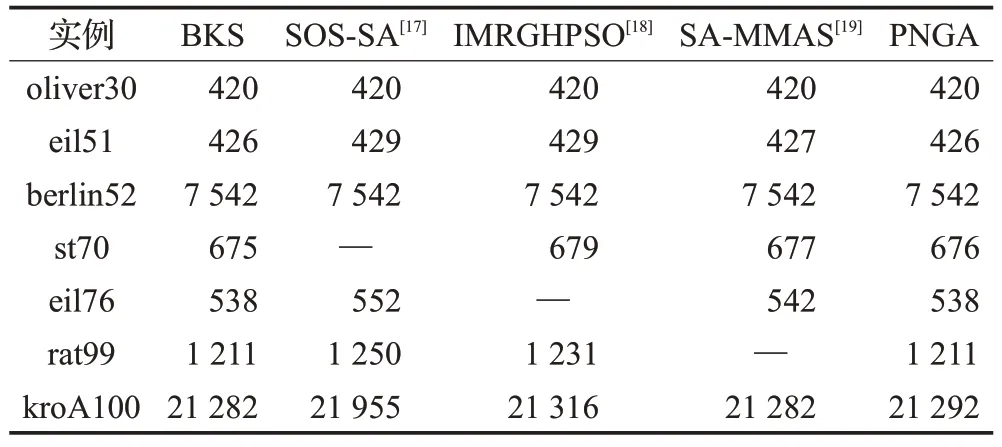
表3 PNGA和主流啟發(fā)式算法最優(yōu)值對(duì)比

從表3可以看出，PNGA在最優(yōu)值上均優(yōu)于IPCO和IMRGHPSO。除了kroA100略次于SA-MMAS外，平均結(jié)果略優(yōu)于SA-MMAS。PNGA部分實(shí)例雖然沒(méi)有達(dá)到最優(yōu)水平，但在結(jié)果上相對(duì)優(yōu)于其他主流算法。實(shí)驗(yàn)表明，PNGA 具有良好的性能和尋優(yōu)效果，能有效用于求解TSP問(wèn)題。

5 結(jié)束語(yǔ)

本文提出的深度指針網(wǎng)絡(luò)與改進(jìn)遺傳算法相結(jié)合的模型，通過(guò)對(duì)TSP問(wèn)題求解研究。指針網(wǎng)絡(luò)為遺傳算法提供的優(yōu)秀初始種群，優(yōu)化遺傳算法的運(yùn)行能力，加快迭代過(guò)程。在TSPLIB公開(kāi)數(shù)據(jù)集上的多組仿真實(shí)驗(yàn)對(duì)比表明，指針網(wǎng)絡(luò)結(jié)合模型相求解質(zhì)量和收斂速度方面均有顯著提高，比同類初始化方法更為優(yōu)秀；與其他主流啟發(fā)式算法對(duì)比也占優(yōu)，是求解TSP問(wèn)題的有效改進(jìn)方法。如何將指針結(jié)合更為復(fù)雜的組合優(yōu)化問(wèn)題是下一步研究的方向。