寒冷地區有砟單線連續梁橋墩縱向線剛度研究

王 樞

(中鐵十九局集團有限公司 北京 100176)

1 概述

為保證列車運行的安全性和舒適性，提高線路平順性，目前我國廣泛采用跨區間無縫線路、以橋代路的建設方案[1]。 在受溫度荷載、列車豎向活載及制動力作用下，梁軌間會產生縱向相對位移，從而在鋼軌中產生縱向附加應力。 鋼軌縱向附加應力與橋墩縱向水平線剛度關系很大，橋墩線剛度越大，鋼軌伸縮力越大，但制動力越小。 墩臺剛度越大，結構受力偏于保守，但過大的墩臺剛度會大大增加工程造價[2]，因此，研究橋梁墩臺合理剛度限值，保證結構在服役期間滿足要求，具有很大的現實需求。

相關文獻對橋梁合理墩臺縱向剛度進行了一些研究。 《鐵路無縫線路設計規范》[3]提出了簡支梁橋墩臺頂縱向水平線剛度限值；許欣等[4]根據城市軌道交通的特點，研究了城市軌道交通高架橋墩縱向剛度合理值；魏峰等[5]研究了橋梁墩臺縱向線剛度對有砟及無砟軌道橋梁結構的影響，并提出了常用跨度簡支梁橋墩臺縱向線剛度的合理取值；蔡小培等[6]根據梁軌相互作用原理，提出了64 m簡支梁墩頂縱向水平線剛度限值；馬旭峰等[7]研究了不同溫度跨度下，單線連續梁橋鋪設小阻力扣件時固定墩的縱向水平剛度限值。

在對連續梁橋固定墩合理線剛度研究時，存在著較多技術難點，主要有以下幾點：在計算模型方面，目前采用的線- 橋- 墩一體化模型還不夠精細；在既有研究方面，針對特定溫度區劃、不同鐵路等級、不同連續梁長的研究還很缺乏；在限值確定方面，對于不同溫度區劃的鋼軌最高最低軌溫，還未有規范進行明確。 因此，本文在現有研究的基礎上，基于梁軌相互作用理論，采用精細化的梁軌相互作用模型，針對我國寒冷地區客貨共線鐵路、高速鐵路及城際鐵路常用的(32 ＋48 ＋32)m、(40 ＋64＋40)m、(48 ＋80 ＋48)m 及(60 ＋100 ＋60)m 有砟軌道連續梁固定墩合理剛度進行了研究，研究成果可為工程設計提供依據。

2 計算模型及計算參數

2.1 計算模型

橋梁與鋼軌在溫度荷載、列車啟動/制動力作用下會產生縱向相對位移，從而在鋼軌中產生縱向附加力，鋼軌縱向附加力通過梁軌間縱向阻力又會反作用在橋梁中，并傳遞到橋梁墩臺上，因此，鋼軌、橋梁、橋墩是一個相互耦合的受力體系。

目前，國內采用的梁軌相互作用有限元理論計算模型[8-10]大多如圖1 所示，自上而下分別為鋼軌、橋梁及橋墩，在受溫度荷載、列車活載作用下，梁軌間會產生縱向相對位移，從而在鋼軌中產生縱向附加應力，此種模型僅可對伸縮力、制動力及斷軌力計算，梁體在撓曲荷載作用下，梁體上下表面與梁中性軸的位移是不同的，圖1 所示的模型無法考慮這一點，模型還存在一定的不足。

本文采用如圖2 所示的模型，鋼軌、橋梁采用beam3 梁單元模擬；路基上及梁軌間非線性阻力單元采用combin39 非線性單元模擬；墩臺縱向剛度采用combin14 線性單元模擬。 與圖1 相比，在橋梁中性軸每個節點處均設置上緣剛臂，在橋墩位置處設置下緣剛臂，模型可很好地模擬梁體撓曲變形后對鋼軌的影響。 以(60 ＋100 ＋60)m 變截面連續梁為例，建立的模型大樣圖如圖3 所示。

圖1 普通梁軌相互作用模型示意

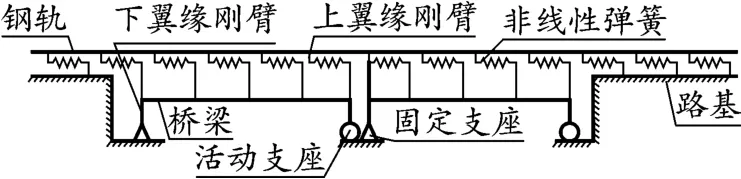
圖2 帶剛臂梁軌相互作用模型示意

圖3 有限元模型大樣圖

2.2 計算參數

連續梁跨長分別取為(32 ＋48 ＋32)m、(40 ＋64＋40)m、(48 ＋80 ＋48)m、(60 ＋100 ＋60)m。 簡支梁墩臺縱向水平線剛度取220 kN/(cm·線)，連續梁兩邊分別布置5 跨32 m 簡支梁，橋梁布置如圖4所示。

圖4 橋跨布置

橋梁鋪設有砟軌道，采用Ⅲ型混凝土軌枕，連續梁及兩邊各兩跨簡支梁采用小阻力扣件，其余橋跨采用常阻力扣件。 計算伸縮力時，混凝土梁取日溫差15 ℃。 根據《鐵路列車荷載圖式》[11]，客貨共線鐵路、高速鐵路及城際鐵路分別采用ZKH、ZK 及ZC 荷載，制動利率取為0.164[12]。

3 墩臺線剛度限值指標確定

為確定連續梁固定墩合理剛度限值，以鋼軌強度條件、鋼軌斷縫值及制動時的快速梁軌相對位移作為限值指標，相關指標計算如下。

3.1 鋼軌強度條件限值

(1)鋼軌容許應力

客貨共線鐵路、高速鐵路及城際鐵路分別采用U75V、U71MnG、U71Mn 鋼軌，根據《鐵路無縫線路設計規范》，鋼軌屈服強度分別為472 MPa、457 MPa、457 MPa，考慮安全系數1.3，計算的鋼軌容許應力分別為363 MPa、351 MPa、351 MPa。

(2)無縫線路溫度應力

將我國溫度地區劃分為嚴寒、寒冷及溫暖區域，其中嚴寒地區選為哈爾濱，溫暖地區選為廣州，寒冷地區取二者中間值。 哈爾濱地區最高軌溫為59.2 ℃，最低軌溫為-38.1 ℃，廣州地區最高軌溫為59.1 ℃，最低軌溫為0 ℃，則計算的嚴寒、溫暖地區溫度應力分別為133 MPa、86 MPa，寒冷地區取二者中間值109 MPa。

(3)鋼軌動彎應力

客貨共線鐵路軸重為25 t，時速160 km，最小曲線半徑1 600 m；客運專線軸重為17.5 t、時速250 km，最小曲線半徑2 800 m；城際鐵路軸重為16 t，時速200 km，最小曲線半徑2 000 m；鋼軌截面參數按60 N軌磨耗6 mm 計。 經計算，客貨共線、客運專線及城際鐵路動彎應力計算值分別為175 MPa、124 MPa、117 MPa。

(4)限值確定

以鋼軌強度條件為橋墩最小線剛度取值控制因素，即：

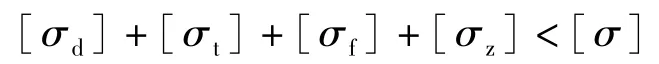
式中，[σ]為鋼軌容許應力；[σd]為鋼軌動彎應力；[σt]為鋼軌溫度應力；[σf]為鋼軌附加應力。

根據工程經驗，列車荷載作用下大跨度橋梁撓曲力小于伸縮力，因此本文鋼軌附加力取伸縮力，不計算撓曲力。

根據上式，可反求得寒冷地區的客貨共線鐵路、高速鐵路及城際鐵路鋼軌強度條件允許限值分別為79 MPa、118 MPa、125 MPa。

3.2 鋼軌斷縫值限值

橋上無縫線路應進行鋼軌斷縫值檢算，根據《鐵路無縫線路設計規范》，鋼軌斷縫值一般情況下取70 mm，困難條件下取90 mm。 為考慮不利工況，本文鋼軌斷縫值限值取70 mm。

3.3 梁軌快速相對位移

當列車在線路上緊急制動時，車輪通過輪軌黏著作用將列車荷載傳遞到鋼軌上，一部分縱向力傳遞到路基上，一部分經梁體傳遞到橋梁下部基礎上。 鋼軌與橋梁間會在短時間內產生縱向相對位移，相關規范規定梁軌快速相對位移不得超過4 mm。本文將制動荷載作用下梁軌快速相對位移作為限值標準之一。

4 工況計算

分別計算寒冷地區有砟軌道采用小阻力扣件時，客貨共線鐵路、高速鐵路及城際鐵路采用(32 ＋48 ＋32)m、(40 ＋64 ＋40)m、(48 ＋80 ＋48)m 及(60 ＋100 ＋60)m 連續梁時的鋼軌伸縮力、鋼軌制動力、梁軌相對位移及鋼軌斷縫值，在此基礎上，提出不同跨度連續梁固定墩合理剛度限值。

4.1 客貨共線鐵路

連續梁及其兩邊各兩跨簡支梁上鋪設小阻力扣件，采用本文第2 章中計算參數，對不同跨度連續梁采用不同固定墩線剛度下的鋼軌伸縮力、鋼軌制動力、梁軌相對位移及鋼軌斷縫值進行計算，相關計算結果如表1 所示。

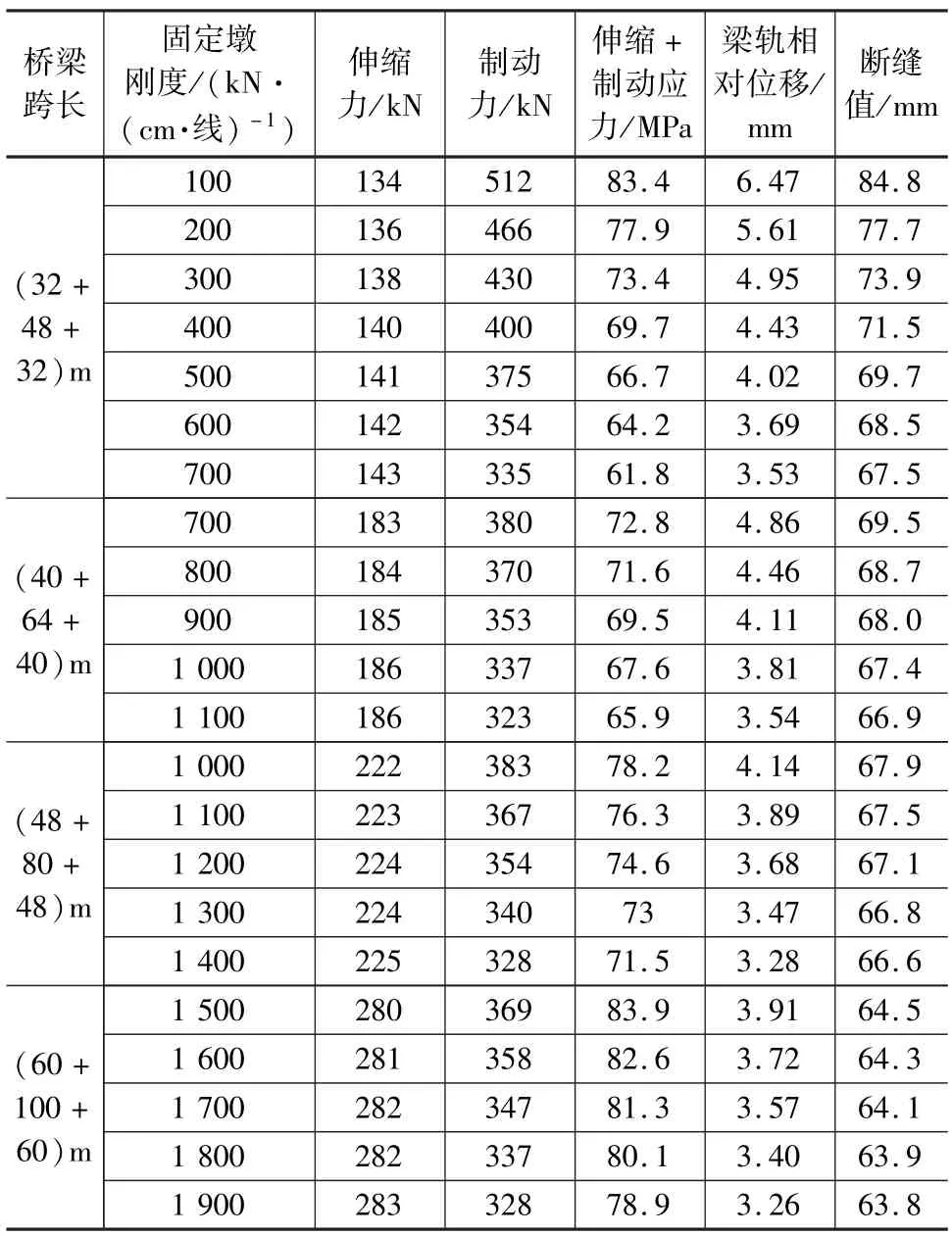
表1 客貨共線鐵路計算結果

以(32 ＋48 ＋32)m 連續梁固定墩為600 kN/(cm·線)為例，計算的鋼軌伸縮力、制動力分別如圖5、圖6 所示，伸縮力、制動力隨固定墩剛度變化如圖7 所示，梁軌相對位移及斷縫值隨固定墩剛度變化如圖8 所示。

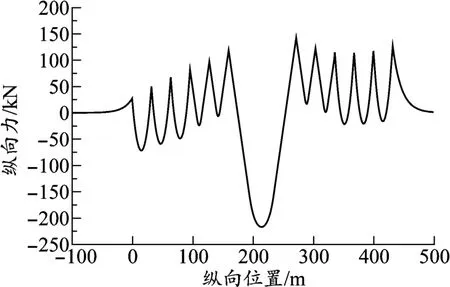
圖5 (32 ＋48 ＋32)m 連續梁鋼軌伸縮力

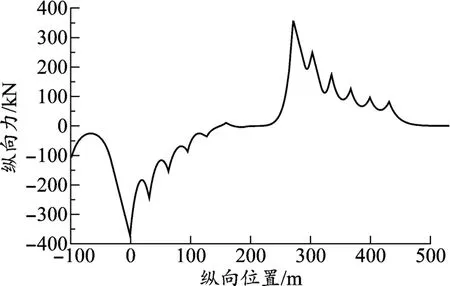
圖6 (32 ＋48 ＋32)m 連續梁鋼軌制動力

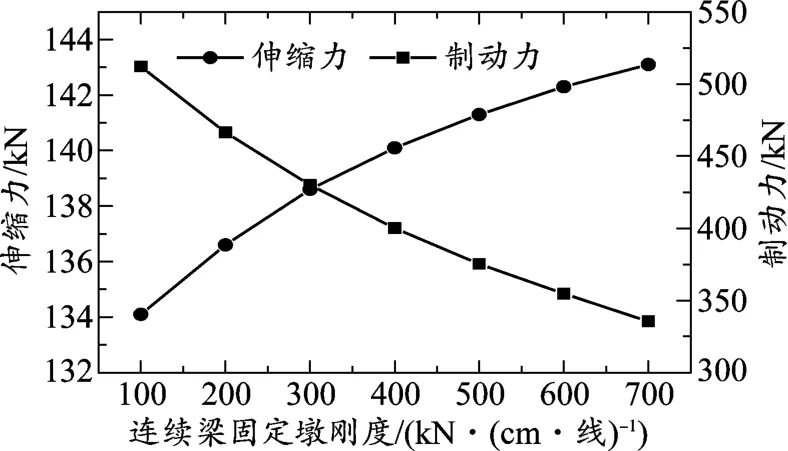
圖7 (32 ＋48 ＋32)m 連續梁伸縮力、制動力隨固定墩剛度變化

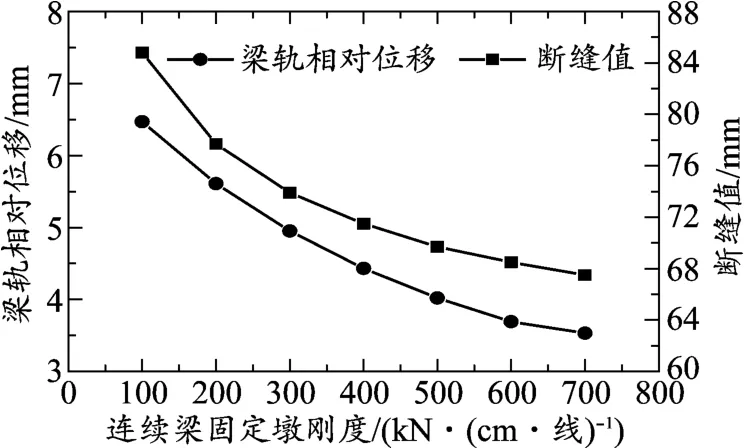
圖8 (32 ＋48 ＋32)m 連續梁梁軌相對位移及斷縫值隨固定墩剛度變化

從表1 及圖7、圖8 可以看出，在簡支梁墩剛度不變的情況下，隨著連續梁固定墩剛度的增大，鋼軌伸縮力呈增加趨勢，鋼軌制動力、梁軌相對位移及鋼軌斷縫值呈下降趨勢。 以(32 ＋48 ＋32)m 連續梁為例，固定墩剛度從100 kN/(cm·線)增加到700 kN/(cm·線)時，鋼軌伸縮力從134 kN 增加到143 kN，增幅6.7%；鋼軌制動力從512 kN 減小到335 kN，降幅34.4%；梁軌相對位移從6.4 mm 減小到3.5 mm，降幅45.4%；鋼軌斷縫值從84.8 mm 減小到67.5 mm，降幅20.4%。由此可知，連續梁固定墩剛度對鋼軌伸縮力影響較小，對制動力、梁軌相對位移及鋼軌斷縫值影響較大。 從圖7、圖8 還可以看出，鋼軌制動力、梁軌相對位移及鋼軌斷縫值隨著墩剛度的增大先快速減小，之后減小幅度放緩。

客貨共線鐵路鋼軌強度條件限值為79 MPa，分析表1 可知，對于(32 ＋48 ＋32)m 連續梁，當固定墩剛度為200 kN/(cm·線)時，鋼軌伸縮力與制動力之和為77.9 MPa，滿足鋼軌強度條件，但此時梁軌相對位移及斷縫值均超限。 綜合三者，可確定(32＋48 ＋32) m 連續梁固定墩合理剛度限值為600 kN/(cm·線)。 采用相同的判定方法，可分別確定(40 ＋64 ＋40)m、(48 ＋80 ＋48)m 及(60 ＋100 ＋60)m 連續梁固定墩剛度限值為1 000 kN/(cm·線)、1 100 kN/(cm·線)及1 900 kN/(cm·線)。

4.2 客運專線鐵路

對客運專線鐵路不同跨度連續梁采用不同固定墩線剛度下的鋼軌伸縮力、鋼軌制動力、梁軌相對位移及鋼軌斷縫值進行計算，計算結果如表2所示。

表2 客運專線鐵路計算結果

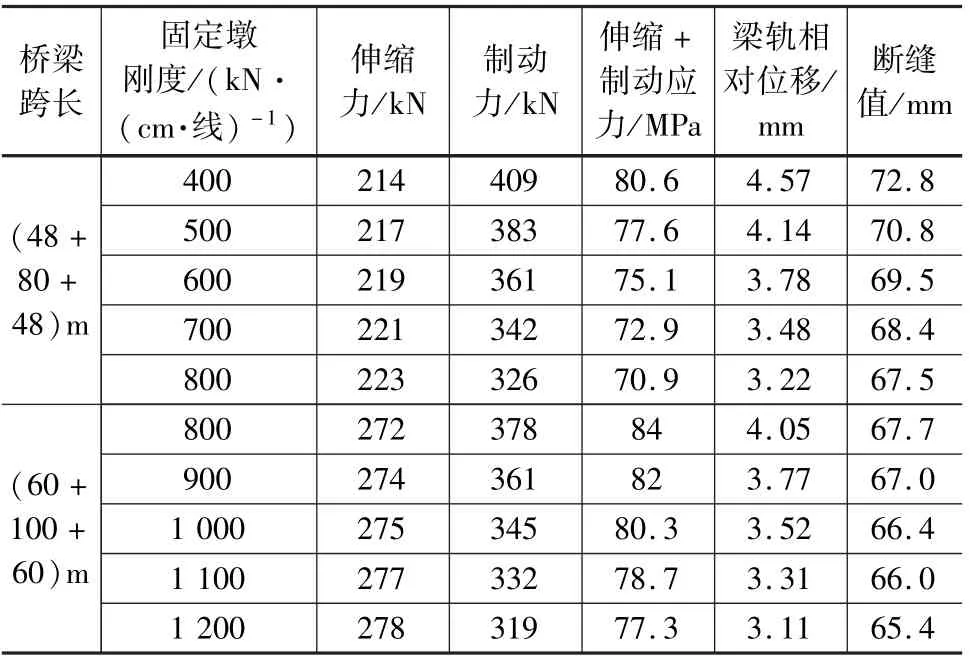
續表2

客運專線鐵路鋼軌伸縮力、鋼軌制動力、梁軌相對位移及鋼軌斷縫值隨墩剛度變化同客貨共線鐵路，此處不再贅述。 對比表1 和表2 可知，相同跨度及固定墩剛度下，客運專線計算的制動力及梁軌相對位移要遠小于客貨共線鐵路，主要原因是客貨共線鐵路軸重較大。

客運專線鐵路鋼軌強度條件限值為118 MPa，分析表2 可知，由于動車組軸重較輕，計算的不同跨度橋梁鋼軌伸縮力與制動力之和遠小于118 MPa，因此，鋼軌強度不是客運專線橋墩剛度控制條件。 綜合梁軌相對位移及鋼軌斷縫值，可分別確定(32 ＋48 ＋32)m、(40 ＋64 ＋40)m、(48 ＋80 ＋48)m 及(60 ＋100 ＋60)m 連續梁固定墩剛度限值為500 kN/(cm·線)、600 kN/(cm·線)、600 kN/(cm·線)及900 kN/(cm·線)。

4.3 城際鐵路

對城際鐵路不同跨度連續梁采用不同固定墩線剛度下的鋼軌伸縮力、鋼軌制動力、梁軌相對位移及鋼軌斷縫值進行計算，相關計算結果如表3 所示。

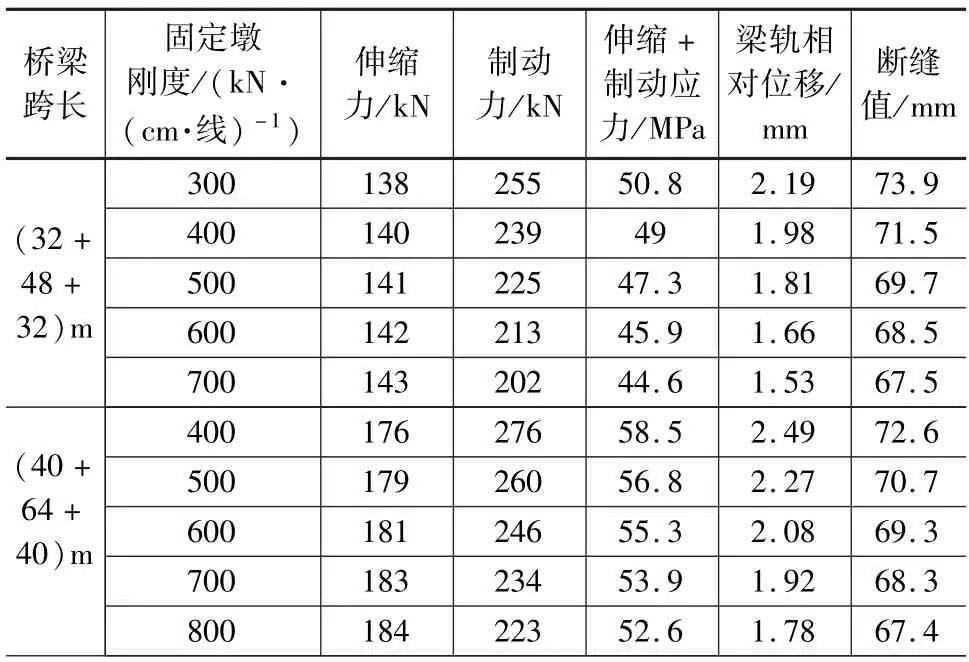
表3 城際鐵路計算結果

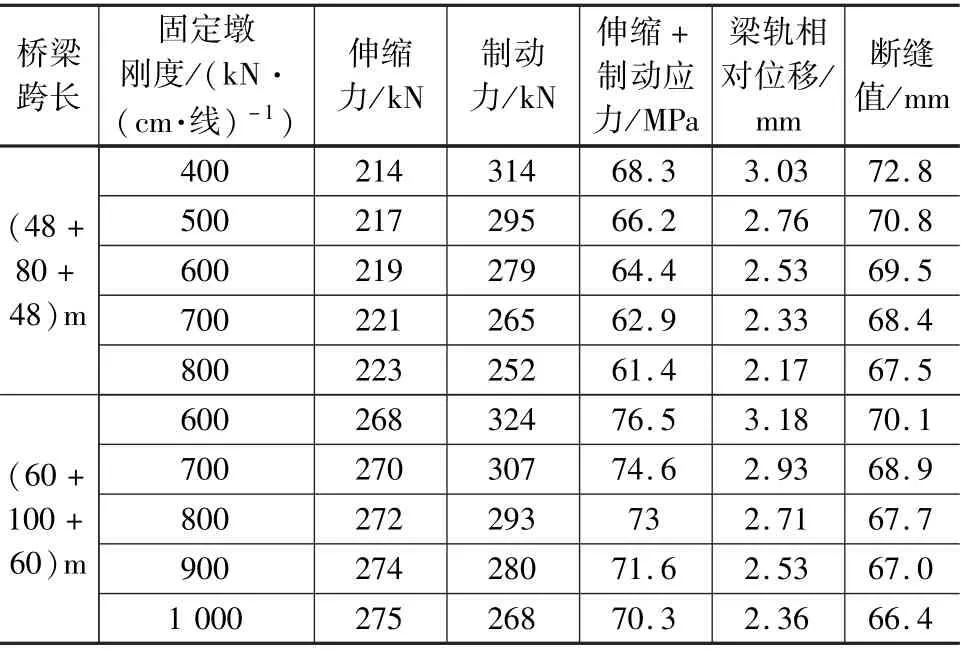
續表3

城際鐵路鋼軌伸縮力、鋼軌制動力、梁軌相對位移及鋼軌斷縫值隨墩剛度變化同客貨共線鐵路。 對比表1、表2、表3 可知，相同跨度及固定墩剛度下，城際鐵路計算的制動力及梁軌相對位移最小，主要原因是城際鐵路采用ZC 活載，因此計算結果較小。

城際鐵路鋼軌強度條件限值為125 MPa，分析表3 可知，對于城際鐵路，鋼軌強度條件也不是橋墩剛度控制條件。 綜合梁軌相對位移及鋼軌斷縫值，可分別確定(32 ＋48 ＋32)m、(40 ＋64 ＋40)m、(48 ＋80 ＋48)m 及(60 ＋100 ＋60)m 連續梁固定墩剛度限值為500 kN/(cm·線)、600 kN/(cm·線)、600 kN/(cm·線)及700 kN/(cm·線)。

4.4 連續梁固定墩合理剛度限值

綜合前面計算結果，寒冷地區有砟軌道采用不同跨度連續梁時，對于不同鐵路等級，固定墩的合理剛度限值如表4 所示。

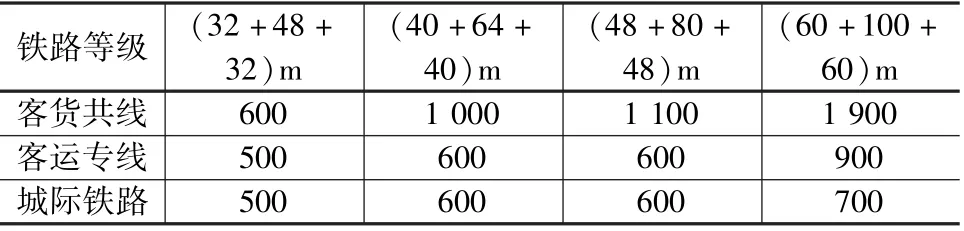
表4 連續梁橋墩頂縱向水平線剛度限值 kN/(cm·線)

5 結束語

本文針對客貨共線鐵路、高速鐵路及城際鐵路常用的(32 ＋48 ＋32)m、(40 ＋64 ＋40)m、(48 ＋80＋48)m 及(60 ＋100 ＋60)m 有砟單線連續梁橋，研究了連續梁橋墩縱向水平線剛度對鋼軌伸縮力、制動力、斷縫值及梁軌相對位移的影響，并在此基礎上，提出了寒冷地區不同鐵路等級、不同連續梁跨長下的合理墩剛度限值。 研究得到以下結論：

(1)隨著連續梁固定墩剛度的增大，鋼軌伸縮力呈增加趨勢，鋼軌制動力、梁軌相對位移及鋼軌斷縫值呈下降趨勢，且其變化幅度在開始時較大，之后趨于平緩。

(2)對于寒冷地區客貨共線鐵路，由于其鋼軌強度限值為79 MPa，因此連續梁橋墩限值由鋼軌強度條件、鋼軌斷縫值及梁軌相對位移共同確定。

(3)對于寒冷地區客運專線及城際鐵路，連續梁橋墩限值主要由鋼軌斷縫值及梁軌相對位移控制。

(4)由于客貨共線鐵路軸重大，因此其合理剛度限值要大于客運專線及城際鐵路。