基于三維混沌與小波變換的彩色圖像加密方法研究

潘文歆

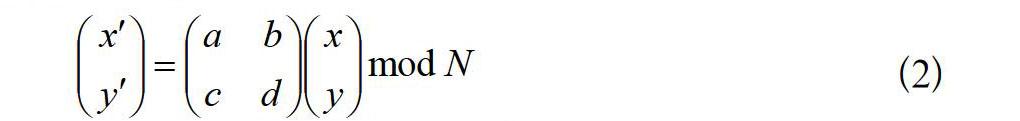
摘要：通過圖像加密可以保證圖像信息的安全存儲和傳輸，本文對彩色圖像首先進行小波變換，使用三維混沌系統和Arnold變換來對圖像對應的低頻子帶系數矩陣和高頻子帶系數矩陣進行隨機分塊和對矩陣元素的位置進行移動與置亂，獲得對應的加密矩陣，之后對加密矩陣使用小波逆變換，就生成了原彩色圖像的加密圖像。實驗結果說明，這種方法的密鑰空間大，密鑰的敏感度較高，可以獲得較大的加密強度。

關鍵詞：彩色圖像;三維混沌系統;加密算法;小波變換;Arnold變換

中圖分類號：TP309.7 文獻標識碼：A 文章編號：1007-9416（2020）08-0123-03

0 引言

隨著圖像和多媒體信息的廣泛使用，保障圖像信息的安全存儲和傳輸已經成為人們關注的一個重要方面，對此的一種有效方法是對圖像進行加密操作[1-3]。在對圖像做加密時，可以針對圖像的像素直接進行加密操作，也可以先對圖像進行一些變換例如小波變換，在此基礎上再進行加密操作[4]。

小波變換是把圖像的像素矩陣變換到頻域，然后對頻域的數據進行處理，來實現對圖像的處理，其特點是可以對圖像信號的局部細節信息進行細致分析。離散小波變換的定義如下：

設，a0是大于0的常數，離散小波為 ，這里j， kZ。對一個給定的函數f（t），它對應的離散小波變換為：。

當信號f（t）取離散值f（k） 時，這時它的離散二進小波變換為：。

離散小波逆變換為：。

把一副圖像進行小波分解后，該圖像就變成了四個不同的部分：LL、LH、HL和HH，其中LL為圖像的近似部分即低頻部分，LH為水平方向上圖像的近似部分，HL為垂直方向上圖像的近似部分，HH為對角方向上圖像的近似部分，除了LL之外，LH，HL和HH都對應于圖像的細節部分。

對經過小波變換的一副彩色圖像，本文首先使用三維混沌系統和Arnold變換來對低頻子帶系數矩陣和高頻子帶系數矩陣進行隨機分塊，然后對這些矩陣元素的位置進行移動和置亂，來實現對彩色圖像的加密。

1 混沌映射

由混沌映射或混沌系統所產生的序列具有對初值和參數的敏感性、隨機性、遍歷性等一些獨特的性質。當輸入的初始參數值發生微小變化時，就會引起輸出序列的值有很大的不同，差異較大;若混沌序列迭代次數越多，其序列在一定范圍內能遍歷趨近無窮的狀態數[5-6]。本文使用如下的三維混沌系統，它的定義如下：

其中當λ=35，β=3和j=28時，系統呈現混沌狀態。把該系統進行時域離散化之后，得到的三個輸出序列{xn}，{yn}和{zn}都是無規律分布的混沌序列。在本文中將使用這三種混沌序列來進行彩色圖像的加密。

2 加密的過程與步驟

對給定的一幅大小為N×N圖像，可以進行多種數字化處理，并獲得一個二維離散的數字矩陣。在這種矩陣中的每個元素就代表了圖像的相關信息。如果把該矩陣中元素的位置進行移動和置亂，就可以得到一個與原圖像相比混亂無章的圖像，從而可以實現對圖像的加密。對元素的位置的移動和置亂，本文使用Arnold變換，該變換的數學表達式如下：

這里（x，y）和（x′，y′）分別表示一個元素在變換前和變換后的位置坐標，mod表示求余運算，它是保證與圖像對應的數據矩陣在進行Arnold變換后仍然落在原先的圖像區域內。Arnold變換的參數a，b，c和d需要滿足如下條件：|ad-bc|=1。例如，a=2，b=5，c=1，d=3。如果對一幅圖像進行多次Arnold變換，而且每一次都對參數a，b，c和d選取不同值時，就可以達到較滿意的效果。

對Arnold變換的參數值的選取，我們采用的方法如下：對參數a，b和c的值，分別從三維混沌系統所產生的混沌序列{xn}，{yn}和{zn}中選取，由于這種混沌序列的值是實數，因此在選取之后需要對它們進行取絕對值和取整運算，然后再作為參數a，b和c的值。在確定了這三個參數a，b和c的值之后，通過使用表達式 |ad-bc|=1，來求出參數d的值。

對一副彩色圖像，加密的過程為：首先對原圖像進行小波變換，得到它的頻率系數矩陣;其次，對頻率系數矩陣的子矩陣進行Arnold變換，以對這些子矩陣進行置亂，實現對它們的加密，并由此獲得加密矩陣;第三，對加密矩陣使用小波逆變換，就生成了原彩色圖像的加密圖像。具體的算法實現步驟如下。

第1步：對一副給定的大小為N×N彩色圖像，通過小波變換，得到它的頻率系數矩陣。

第2步：從圖像對應的頻率系數矩陣中提取出低頻子帶系數矩陣LL和高頻子帶系數矩陣HL、LH和HH。

第3步：使用混沌系統產生一個正整數m，其方式如下：首先使用混沌系統（1）產生三個混沌序列{xn}，{yn}和{zn}，然后從這三個序列中分別隨機選取一個值出來，并把所選出的這三個值取絕對值然后再相加，之后取整，就作為m的值。

第4步：對矩陣LL、HL、LH和HH，把每個矩陣分塊成多個即2m個子矩陣。

第5步：對上一步中所獲得的矩陣LL、HL、LH和HH的每個子矩陣，使用Arnold變換對它們進行置亂，以實現對它們的加密，把使用的加密密匙分別記為KeyLL，KeyHL，KeyLH和KeyHH，該加密密匙即是在Arnold變換中的參數a，b，c和d，它們是根據混沌系統（1）所產生的混沌序列來進行選取的。

第6步：把在第5步中所得到的每個經加密的子矩陣組合起來，就構成了LL、HL、LH和HH的加密矩陣。

第7步：對LL、HL、LH和HH的加密矩陣使用小波逆變換，就生成了原彩色圖像的加密圖像。

在算法的第5步中，由混沌系統（1）所產生的值需要進行取整操作，才能作為參數a，b，c和d的值，并且滿足 |ad-bc|=1。同時，對每一個子矩陣都設計對應的不相同的密匙KeyLL，KeyHL，KeyLH和KeyHH，以進一步提高加密的強度。

對算法的加密圖像進行解密，解密的過程是算法的逆過程，其步驟如下：首先分別從加密圖像中提取出LL、HL、LH和HH的加密矩陣，然后使用加密的密匙KeyLL，KeyHL，KeyLH和KeyHH，以及進行Arnold逆變換，來獲得矩陣LL、HL、LH和HH的每個子矩陣，之后把這些子矩陣組合起來，得到圖像的四個子帶系數矩陣LL、HL、LH和HH，使用這四個子帶系數矩陣和小波逆變換即小波重構來得到原彩色圖像。

3 實驗結果

我們通過MATLAB編程對算法進行了實現，并對一些彩色圖像進行了實驗，所使用的微型計算機的處理器和內存分別為2.80GHz和8GB。圖1是對彩色lena圖像的實驗結果，圖1（a）是原圖像，圖1（b）是使用算法進行加密后的圖像，圖1（c）是對圖1（b）做解密之后還原的圖像。圖2（a）和圖3（a）分別是House圖像和Horse圖像，圖2（b）和圖3（b）是采用算法對原圖像進行加密后的圖像，圖2（c）和圖3（c）是對圖2（b）和圖3（b）進行解密之后還原的圖像。

如上的這些實驗結果表明，本文設計的算法具有較高的加密強度，可以取得良好的加密效果。由于在對彩色圖像的加密過程中對原始圖像進行了分塊，對各個子圖像所對應的矩陣LL、HL、LH和HH采用了不同的多個密匙進行置亂，使圖像的各方向相鄰像素的相關性系數達到很小，接近于0，從而大大增加了加密的強度。

由于上文算法是同時對四個矩陣LL、HL、LH和HH進行操作和加密處理，這就避免了常規方法中只對矩陣LL進行加密處理所帶來的加密強度不高的問題，因此本文的算法也具有較強的抗攻擊能力。此外，在采用混沌系統的圖像加密的早期研究中，人們主要使用低維混沌系統，由于這種混沌系統的結構簡單而且參數較少，導致了相應加密算法的密鑰空間比較小并且容易被攻破。本文對彩色圖像的加密采用的三維混沌系統，由于具有較大的參數空間和較復雜的結構，因此可以使得加密算法的密鑰空間得到擴大，從而可以進一步提高密鑰的敏感度。

4 結語

對彩色圖像的加密，本文對圖像先進行小波變換，然后使用三維混沌系統和Arnold變換來對低頻子帶系數矩陣和高頻子帶系數矩陣進行隨機分塊和對矩陣元素的位置進行移動和置亂，這種方法由于采用了具有較大的參數空間和較復雜結構的三維混沌系統，從而可以提高密鑰的敏感度并增大加密的強度。

參考文獻

[1] Abdullah Alghafis，Faiza Firdousi，Majid Khan.An efficient image encryption scheme based on chaotic and deoxyribonucleic acid sequencing[J].Mathematics and Computers in Simulation，2020，177：441-466.

[2] Ali Mansouri，Xingyuan Wang.A novel one-dimensional sine powered chaotic map and its application in a new image encryption scheme[J].Information Sciences，2020，520：46-62.

[3] 胡春杰，嵇海祥，牛智星，等.基于改進Arnold映射二次置亂的圖像加密算法[J].計算機與數字工程，2019，47（7）：1783-1787.

[4] 陳娜，毋江波.基于離散小波變換的離散正交S變換域圖像加密算法[J].光學技術，2019，45（3）：348-354.

[5] 李付鵬，劉敬彪，王光義，等.基于混沌集的圖像加密算法[J].電子與信息學報，2020，42（4）：981-987.

[6] 馬聰，李國東.基于L-K雙混沌系統的彩色位級圖像加密算法[J].計算機應用與軟件，2020，37（3）：322-326.