低速陶瓷球侵徹明膠研究

張志倩,趙太勇,印立魁,付建平,于寅業,張佳玉

(1.中北大學 機電工程學院 山西 太原 030051;2.中北大學 地下目標毀傷技術國防重點實驗室,山西 太原 030051;3.晉西工業集團有限責任公司,山西 太原 030051)

在現代戰爭中,隨著戰斗部技術的快速發展,以高性能、低成本的陶瓷球等為代表的新型戰斗部毀傷元應運而生。與普通鎢合金、鋼質破片相比,陶瓷球具有強度高、比動能大、價格低廉、容易生產等優點,可對近距離有生力量進行有效打擊。創傷彈道學研究,常采用明膠作為人體組織的替代物,因此研究低速陶瓷球侵徹明膠對人體殺傷機理具有重要意義[1-2]。近年來,國內外學者對球形破片侵徹明膠的運動進行了大量的試驗與理論研究,其中莫根林等[3-4]根據球形破片侵徹明膠的空腔實驗數據,推導出空腔的運動為正弦運動;劉坤等[5]引入明膠抗力進一步完善了球形破片侵徹明膠的修正力學模型;文獻[6]通過無網格數值方法(SPH方法)研究彈丸在人體組織替代物中的滲透;文獻[7]研究了在較低的沖擊速度(120 m/s)下明膠材料對球形鋼彈丸穿透的響應;文獻[8]通過實驗和計算方法研究了中等速度下鋼球在明膠中的侵徹,通過理論計算出的明膠一個點的壓力、瞬時空腔尺寸時間歷程與相應的實驗測量的時間歷程吻合得很好;金永喜等[9]利用相似理論推導出明膠瞬時空腔效應的相似準則方程,從而建立了明膠靶標與肌肉目標的空腔效應等效模型。

目前,對陶瓷材料作為毀傷元的毀傷機理和明膠侵徹響應特性有了初步認識,但針對陶瓷球低速侵徹明膠的研究相對較少,進行低速陶瓷球對明膠的毀傷效應研究是武器系統效能評估的重要內容,且低速陶瓷球具有低附帶毀傷特性,具有重要軍事意義。故需要開展低速陶瓷球侵徹明膠的研究。本文通過彈道沖擊試驗,基于數值模擬和能量守恒理論計算研究了不同直徑和不同沖擊速度下陶瓷球侵徹明膠的規律。

1 理論分析

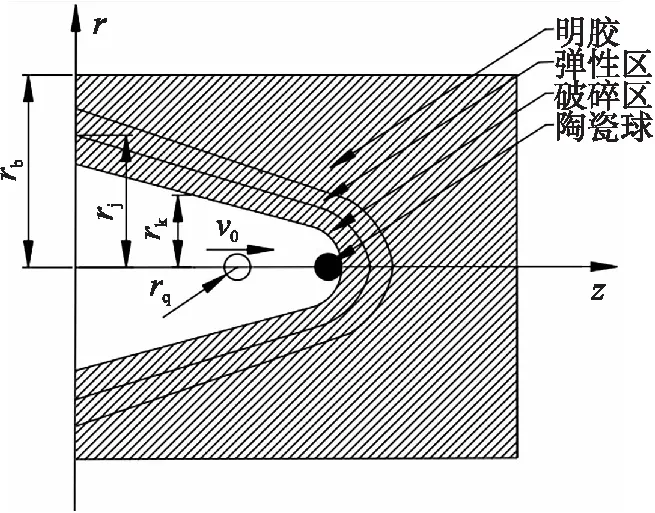
圖1 理論分析模型

陶瓷球侵徹明膠是動態過程,明膠包含變形能和動能,明膠的破壞可分為破碎區和彈性區。假設陶瓷球釋放的動能全部轉化為明膠徑向運動的動能和明膠的變形能,利用能量守恒原理,對陶瓷球侵徹明膠進行分析。根據文獻[10]中的模型,明膠與陶瓷球的分離點在靠近頭部頂點的位置,隨著侵徹速度降低,分離點逐漸向后移動,直到低到臨界速度(vc=10 m/s±2 m/s)及以下,分離點保持在與侵徹方向垂直的最大橫截面處。如圖1所示,在柱坐標系(z,r)中,rk為明膠形成的空腔半徑,rj為彈性區和破裂區交界位置的半徑,rb為明膠的邊界尺寸,v0為彈丸沖擊速度,rq為陶瓷球半徑。

在彈道某一位置處,取軸向厚度dz的一層明膠為研究對象,該層明膠的動能為[11]

(1)

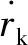
在研究陶瓷球侵徹明膠時的變形能時,假設明膠中球形空腔以很低的速度膨脹,因此空腔周圍有破裂變形區和彈性變形區,動量守恒和質量守恒方程為

(2)

(r-u)2d(r-u)=r2dr

(3)

式中:u為徑向位移,σr為徑向應力,σθ為拉伸應力。

對于破裂區,由邊界條件r=rk,破裂區σθ=0,求解可得:

(4)

(5)

(6)

式中:c1和c2為模量,p為明膠內各向壓力。

當空腔r=rk時,結合動量守恒式(2),則rk處空腔徑向應力為

(7)

由式(4)可得:

(8)

假設邊界條件σr(r=rb)≈0,同理得出:

(9)

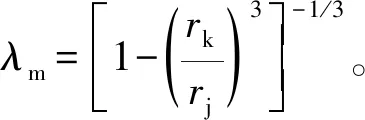
對于破裂變形能,由于σθ=0,聯立式(7)、式(8)可得微元層破裂變形能dEc:

(10)

將邊界條件rb≈∞代入,則可簡化式(9):

(11)

對于彈性區,微元層彈性變形能dEe為

(12)

由能量守恒,有

dEk,p=dEk,g+dEc+dEe

(13)

式中:dEk,p為微元層陶瓷球動能,dEk,g為微元層明膠動能,dEc為明膠微元層破裂變形能。化簡式(13)，整理可得侵徹深度h:

(14)

式中:mp為陶瓷球質量,v0為陶瓷球沖擊速度,λm取值為1.5～2.0。利用Matlab軟件求解超線性方程,可解出侵徹深度h。

2 試驗方法

試驗在室內靶道進行。采用7.62 mm口徑滑膛槍發射,用彈托支撐不同直徑的陶瓷球分別侵徹500 mm×500 mm×300 mm明膠,由測速儀器測量出陶瓷球速度,如圖2所示。

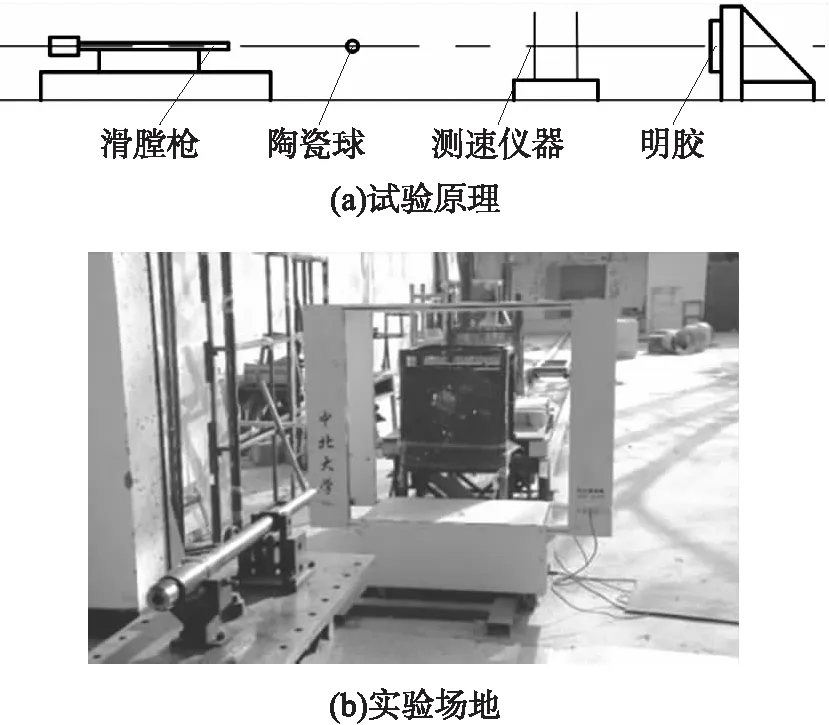
圖2 試驗原理及實驗場地

明膠靶制作過程:明膠顆粒與水的質量配比為1∶5,采用溫度為60 ℃水浴加熱的方式,將明膠顆粒溶于水形成明膠溶液,并在4 ℃的環境下凝固,制成的明膠靶如圖3所示。圖4為d=2 mm,3 mm,5 mm的陶瓷球。

圖3 明膠

圖4 陶瓷球

3 數值模擬方法

圖5 有限元網格模型

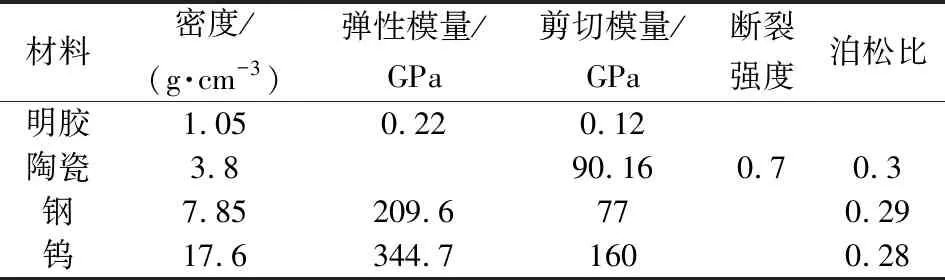
表1 模型材料參數

4 試驗結果及分析

4.1 陶瓷球侵徹明膠理論與試驗的對比

利用d=2 mm,3 mm,5 mm的陶瓷球進行侵徹明膠試驗,結果發現陶瓷球的直徑越大、沖擊速度越高,其在明膠中的侵徹深度越深,試驗結果相關參數如表2所示,表中,d為陶瓷球直徑,v0為沖擊速度,h為侵徹深度。圖6為不同直徑的陶瓷球侵徹試驗結果。

表2 試驗結果

圖6 不同直徑不同速度侵徹明膠試驗結果

將理論計算結果、試驗結果與數值模擬進行對比,發現三者趨勢相同,如圖7所示。文獻[6]和文獻[8]試驗數據為高速球形破片,將其與理論模型值進行對比,如圖8、圖9所示,發現理論侵徹深度與試驗結果誤差在10%以內,說明理論模型可適用低、中、高速度,因而具有一定的參考價值。

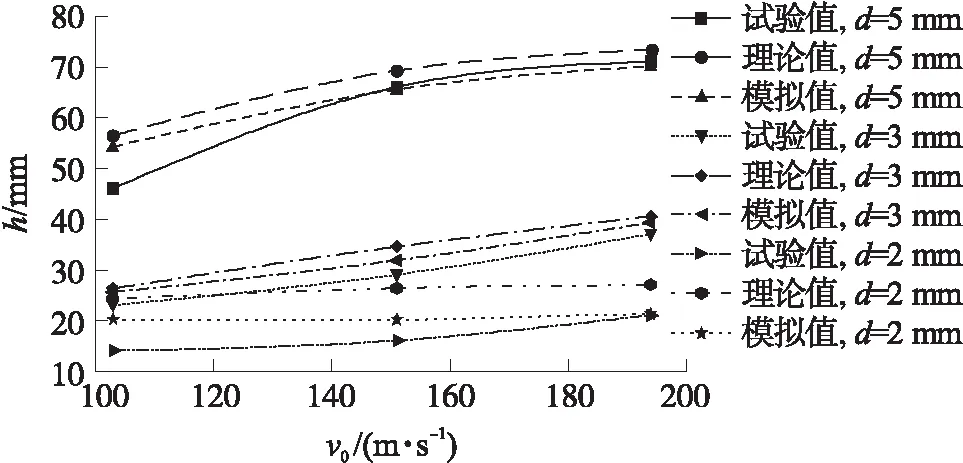
圖7 理論模型、實驗值、數值模擬的對比

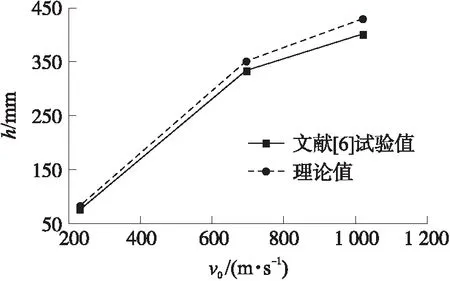
圖8 理論模型與文獻[6]數據的對比

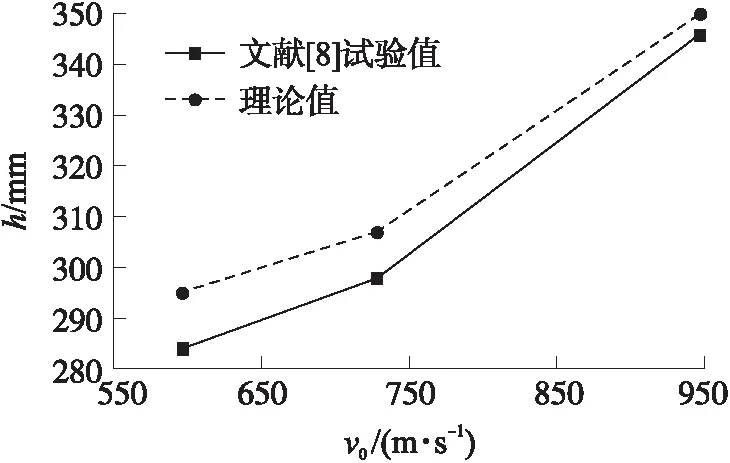
圖9 理論模型與文獻[8]數據的對比

4.2 陶瓷球直徑和沖擊速度對侵徹明膠的影響

通過數值模擬的方法,改變陶瓷球的直徑和沖擊速度,如圖10所示。在0.16 ms時,試驗結果與數值模擬結果中明膠的破壞形態基本吻合,說明本文選取的數值模擬材料參數具有一定的可靠性。明膠的侵徹深度和形成的空腔是評價創傷彈道的重要的殺傷參數,因此,需要進一步研究沖擊速度v0和陶瓷球直徑對侵徹深度h、最大瞬時空腔的影響。圖11為根據試驗數據繪制的陶瓷球直徑和沖擊速度v0對侵徹深度h的影響結果。研究發現:陶瓷球的直徑越大、沖擊速度越高,侵徹深度則越深;且陶瓷球直徑的改變比沖擊速度的改變對侵徹深度的影響更大。因此,低速下陶瓷球的直徑是決定侵徹深度的主要因素。最大空腔直徑隨陶瓷球的直徑和沖擊速度的增加而增加,陶瓷球直徑、沖擊速度對最大空腔直徑dk,m的影響如圖12所示。由圖可見,陶瓷球的直徑和沖擊速度同時影響最大空腔直徑。

圖10 不同陶瓷球直徑、不同速度侵徹明膠的數值模擬結果

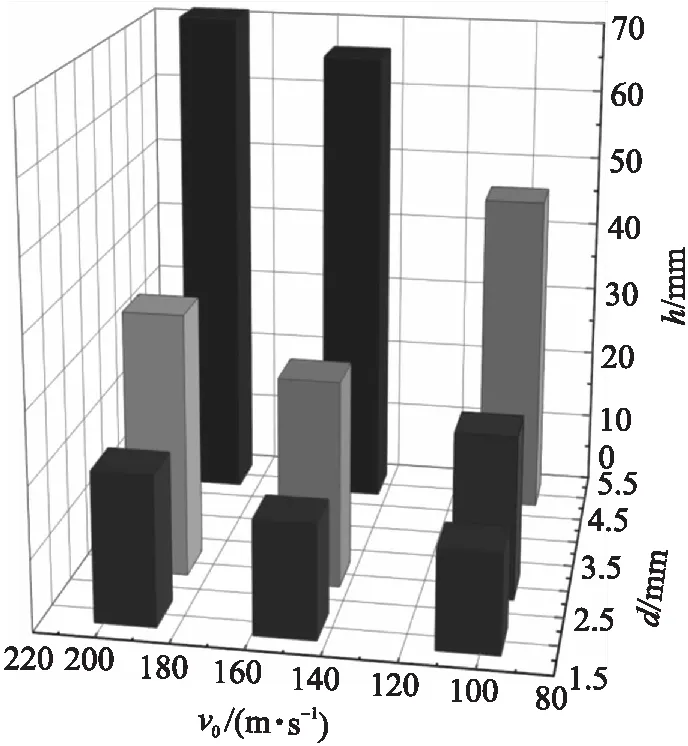
圖11 沖擊速度和陶瓷球直徑對侵徹深度的影響

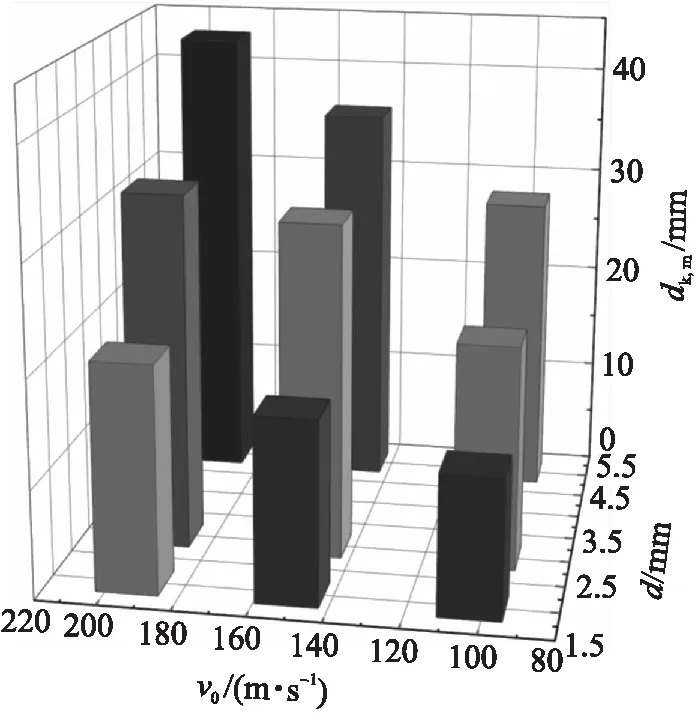
圖12 沖擊速度和陶瓷球直徑對最大空腔直徑的影響

4.3 不同材料的球形破片對侵徹明膠的影響

為研究不同材料的球形破片對侵徹明膠的影響,將陶瓷球、鋼球、鎢球侵徹明膠進行對比。利用數值模擬方法研究直徑d=3 mm的不同材料的球形破片侵徹明膠時的速度v的衰減情況,發現3種材料在初始沖擊速度v0=103 m/s,151 m/s,194 m/s情況下,陶瓷球的速度衰減最快,鋼球和鎢球速度衰減較緩,結果如圖13所示。

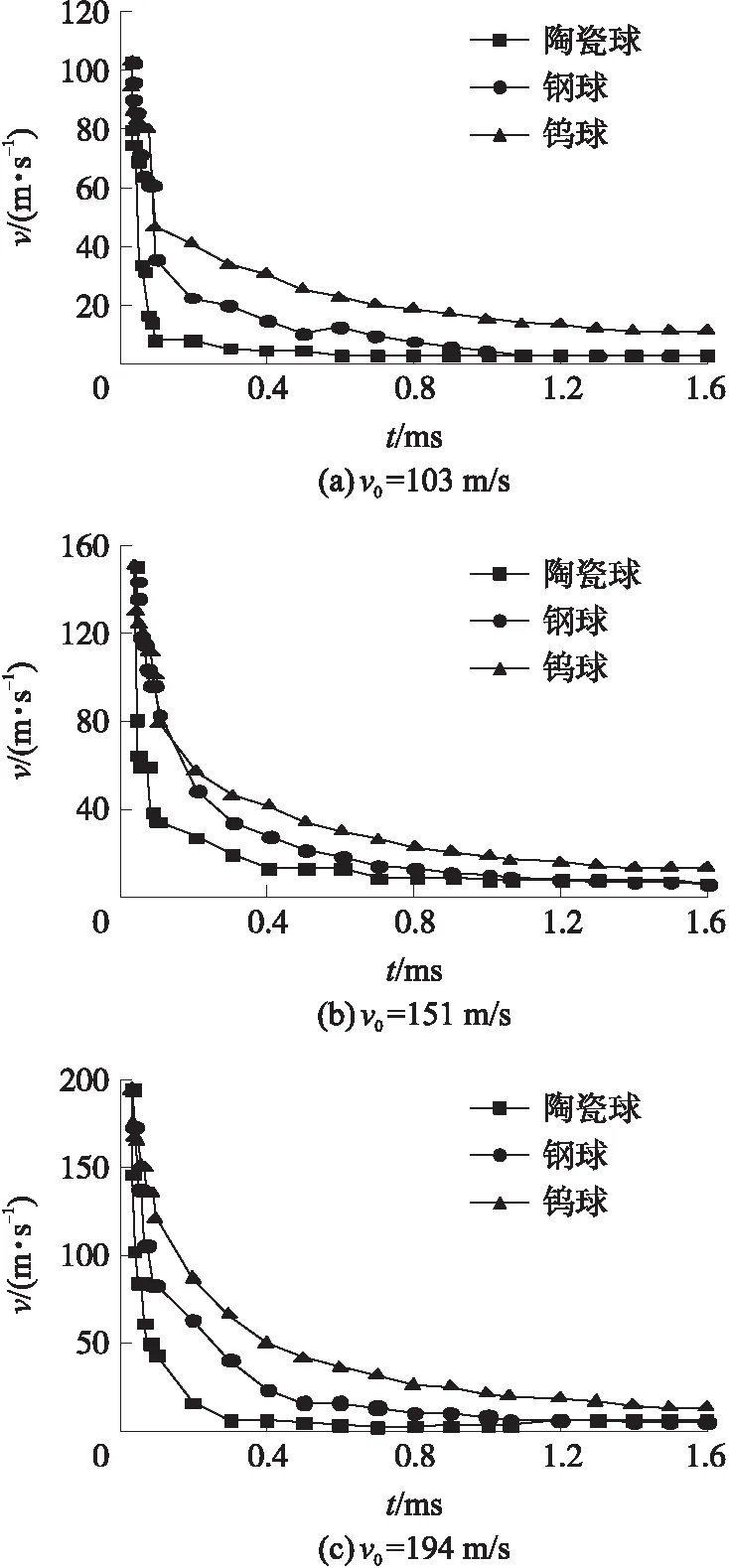
圖13 不同材料球形破片侵徹明膠的速度隨時間的衰減

在研究破片的材料對侵徹深度和最大空腔半徑的影響時,沖擊速度v0分別取103 m/s,151 m/s,194 m/s。由于侵徹深度h與最大空腔半徑rk,m是評價毀傷的重要參數,將二者之和H作為綜合毀傷參數,H與破片初始動能Ek0的關系如圖14所示。根據圖14,陶瓷球、鎢球和鋼球對應的侵徹深度與最大空腔半徑之和H的差異較小。分析其原因:在保證初始動能相同的情況下,隨著密度的增加,破片的半徑減小;而結合式(14)可知,侵徹深度h與最大空腔半徑rk,m反相關。因此,明膠的空腔越大,對應的侵徹深度越小。3種材料的侵徹深度與最大空腔半徑之和H的差異較小,而陶瓷球具有強度高、比動能大、價格低廉、生產容易等優點,更適合作為毀傷元。

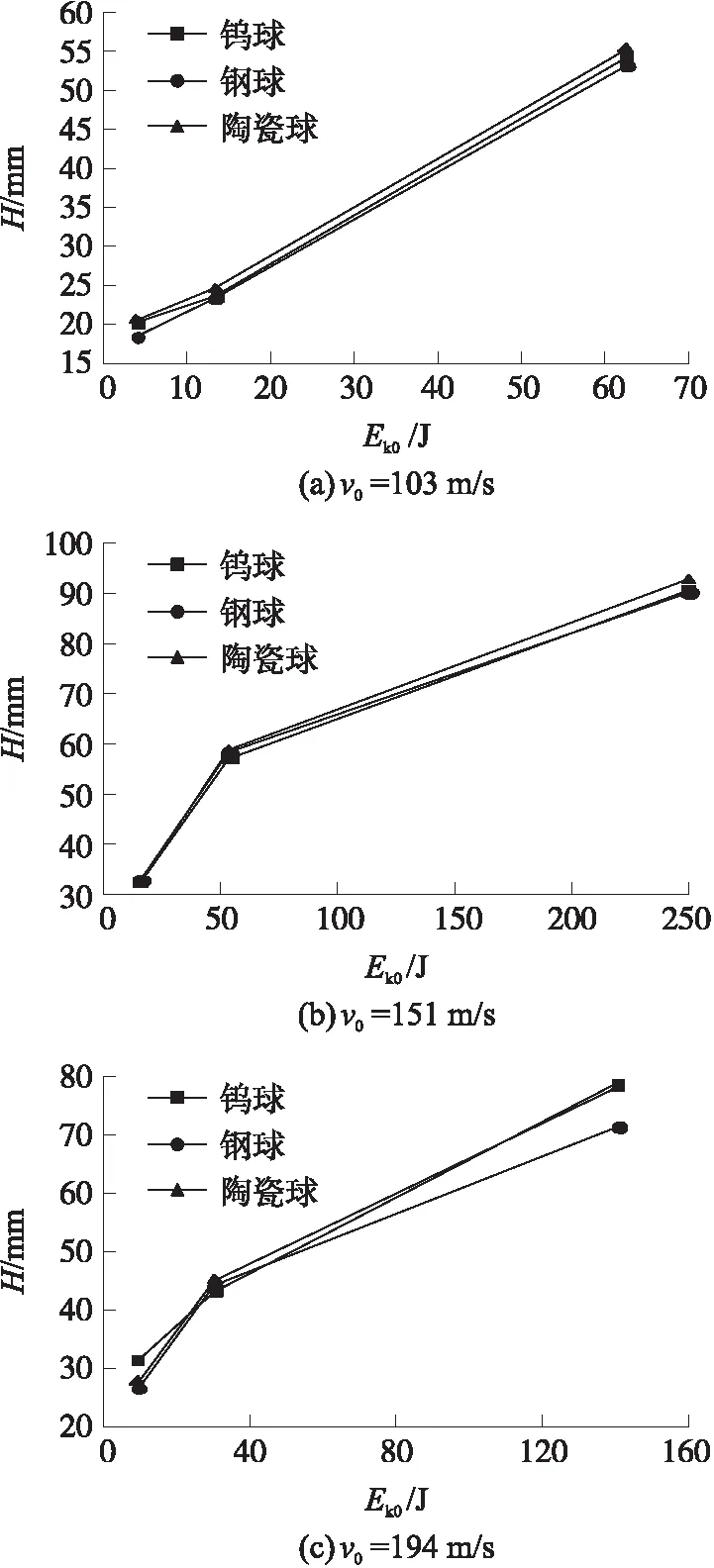
圖14 初始動能對綜合毀傷的影響

4.4 永久空腔的形成

在試驗中發現有永久空腔的現象,見圖15。

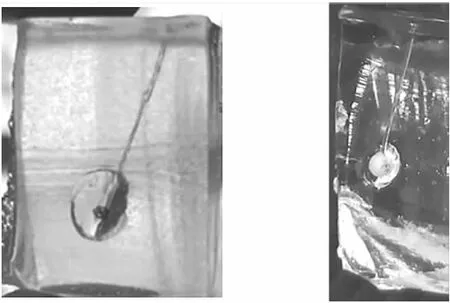
圖15 永久空腔

陶瓷球侵徹明膠產生壓力,開始只有直接作用的質點離開沖擊平衡位置,力的作用和反作用使相鄰質點離開沖擊平衡位置而運動起來,明膠內的擾動在介質中逐漸由近及遠傳播出去而形成應力波。但由于明膠制作工藝中可能存在攪拌不均勻,凝固時明膠的密度不均勻,導致明膠力學特性各異。因此應力波在傳播、反射和相互作用過程中產生差異,明膠產生永久空腔的現象。人體中各種組織密度、結構也存在著不同,也可能產生永久空腔,而永久空腔對人體殺傷有重要影響。

5 結論

本研究通過理論分析、試驗驗證和數值模擬3種方法,對低速陶瓷球侵徹明膠進行研究,得到以下結論:

①本文理論分析模型計算出的陶瓷球侵徹明膠深度與試驗結果有較好的一致性;理論模型具有可靠性,此理論模型可為計算球形破片侵徹明膠的深度提供參考。

②利用試驗和數值模擬的方法改變陶瓷球的直徑和沖擊速度,發現在低速下直徑是影響陶瓷球侵徹明膠深度的主要因素。

③利用數值模擬方法對鎢球、鋼球、陶瓷球在相同初始動能和沖擊速度下侵徹明膠的情況進行對比,發現三者侵徹深度與最大空腔半徑之和差異較小,考慮到侵徹材料自身特點和經濟性,陶瓷球更適合作為毀傷元。