固體復合推進劑火箭發動機侵蝕界限參數的預測方法與應用

陳 軍

(南京理工大學 機械工程學院,江蘇 南京 210094)

內彈道性能是固體火箭發動機的重要性能指標之一,準確獲取相應的侵蝕函數非常困難[1-4]。文獻[5-6]以20世紀70年代末的火焰彎曲理論為基礎[7],建立了火焰彎曲理論侵蝕函數方程,發展了一種能夠預測過氯酸銨(AP)固體復合推進劑速度侵蝕函數和平均侵蝕函數的理論方法。但是該方法還不能解決侵蝕燃燒中存在的臨界侵蝕問題。

文獻[8]基于表觀傳熱理論,Lenoir建立了勒努爾-羅比拉德侵蝕公式(稱為L-R公式), 文獻[9-10]根據實驗結果改進了L-R公式,本文在此基礎上發展了一種能夠預測AP固體復合推進劑侵蝕界限參數(包括界限流速vth和界限燃通比th)的理論方法,并進行了算例驗證。

1 勒努爾-羅比拉德侵蝕公式與侵蝕界限流速的關系

表觀傳熱理論基于傳熱的基本原理,模型簡單,許多結論與實驗符合很好,是目前應用最廣泛的理論。基于傳熱理論建立的改進的L-R公式為

(1)

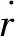
將密流G=ρv代入式(1),并整理為燃氣流速v的影響關系式,得:

(2)

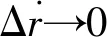
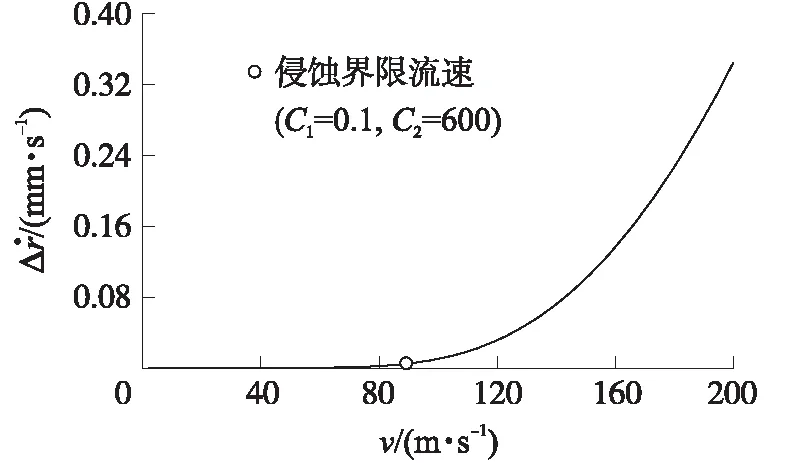
圖1 L-R公式表示的侵蝕燃速增量與臨界侵蝕流速

可見,L-R公式在表達侵蝕界限流速方面具有比較強的合理性。

2 固體火箭復合推進劑侵蝕界限流速預測的理論模型

實驗發現,侵蝕效應只有在燃氣流速達到一定值后才明顯發生。由侵蝕函數ε的定義可得:

(3)

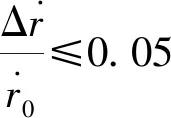
(4)

為侵蝕臨界狀態,對應的密流即為侵蝕界限密流Gth,對應的燃氣流速即為侵蝕界限流速vth。將L-R式(1)代入式(4),可得:

整理為

(5)

將密流G=ρv代入式(5),得:

(6)

式(5)和式(6)即為確定侵蝕界限密流和侵蝕界限流速的一般關系式。由于L-R公式本身的缺陷,直接采用式(5)和式(6)計算結果存在較大誤差,為此引入經驗系數進行改進。

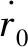
(7)

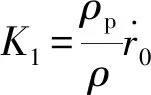
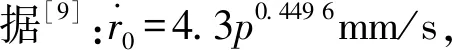
(8)

由于β反映了燃速的大小,β越大燃速也越大,故式(8)在一定程度上反映了燃速對侵蝕界限流速的影響。取β=70,由式(8)可得:vth=120.4 m/s。vth升高,意味著侵蝕效應減小,這與實驗結果一致。

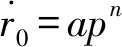
(9)

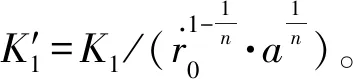
(10)

式(10)即為計算固體火箭復合推進劑侵蝕界限流速的理論公式。對于不同復合推進劑,只要知道其基本燃速公式,即可利用式(10)計算得到相應的侵蝕界限流速。

3 固體火箭復合推進劑侵蝕界限燃通比預測的理論模型

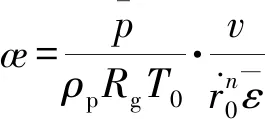
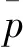
(11)

確定侵蝕界限流速vth后,利用式(10)可以方便地計算得到侵蝕界限燃通比th。

4 理論預測臨界侵蝕流速的應用驗證

解得vth=99.1 m/s。

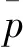
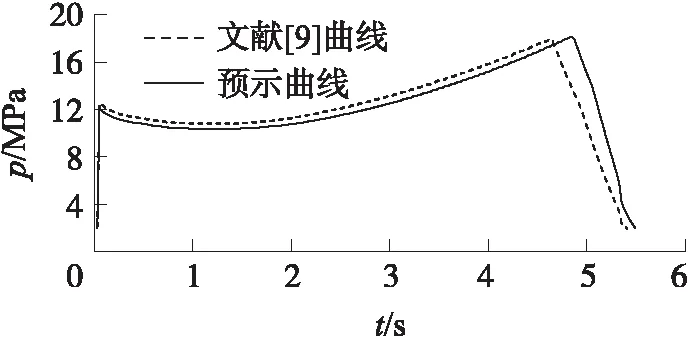
圖2 采用理論侵蝕界限流速預示的內彈道曲線與文獻[9]數據的比較

表1 利用預測的臨界侵蝕流速計算的某固體火箭發動機工作壓強與文獻[9]數據的比較

從圖2中曲線可以看出,預示曲線整體稍微偏低,具有較強的可修正性,即可以通過修正進一步提高預示精度。

將同樣發動機的參數(ρp=1 721 kg/m3,ρpRgT0=1 039.7 kJ/kg)代入式(10),可得該發動機侵蝕界限燃通比th=47.8。應用于該發動機零維內彈道計算的結果如圖3所示;預測計算數據與文獻[10]數據的比較如表2所示,由表2可見計算精度較好,滿足一般工程精度要求。

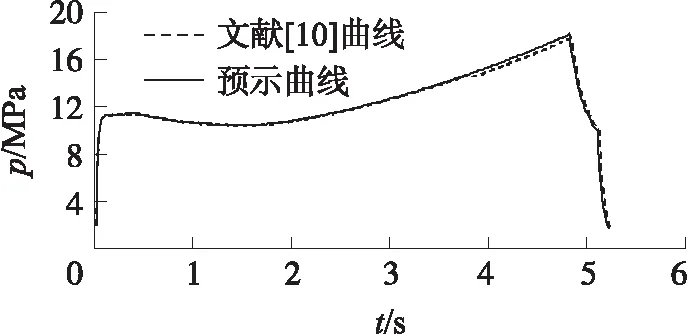
圖3 采用理論侵蝕界限燃通比預示的內彈道曲線與文獻[10]數據的比較

表2 利用預測的臨界侵蝕流速計算的某固體火箭發動機工作壓強與文獻[10]數據的比較

5 理論

為考慮尺寸效應,保留當量直徑dp,則式(7)變為

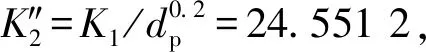
(12)

取dp=0.3 m,代入式(12),可得vth=133.9 m/s。vth升高,意味著尺寸越大的發動機侵蝕效應越小,這與實驗結果一致。由于L-R公式考慮了整個侵蝕燃燒階段的尺寸效應,如果侵蝕界限流速也考慮該效應,計算結果表明,會引起較大誤差,故計算侵蝕界限流速時不再重復考慮尺寸效應。

式中:K?1=K1/pn-1,K?2為經驗系數。仍以前述小口徑發動機為例,取p=10 MPa,則K?1=K1/pn-1=13 055.1,K?2=K2/(10×106)0.449 6-0.8=4 517.9。可得:

(13)

取p=20 MPa,代入式(13),可得vth=70.8 m/s。vth減小,意味著壓強越大的發動機侵蝕效應也越大,這與實驗結果一致。

6 結論

本文通過2種固體復合推進劑火箭發動機的數據分析與應用,說明利用改進的L-R公式建立的預示理論侵蝕界限參數公式是合理的。主要結論如下:

①改進的L-R公式的函數曲線存在明顯的無侵蝕燃燒階段,故該理論用于預測侵蝕界限流速具有比較強的合理性。

③侵蝕界限參數的預示還可考慮尺寸效應和壓強的影響。但由于L-R公式考慮了整個侵蝕燃燒階段的尺寸效應,故計算侵蝕界限參數時不再重復考慮尺寸效應,否則會帶來較大的誤差。

本模型只研究了復合推進劑火箭發動機的侵蝕界限參數,是否適用于其他推進劑還需要進一步研究。