水下機器人-機械臂系統(tǒng)的滑模自抗擾控制

李小崗, 王紅都, 黎 明, 劉 鑫

(1. 中國海洋大學 工程學院, 山東 青島 266100; 2. 四川警學院 偵查系, 四川 瀘州 646000)

水下機器-機械臂系統(tǒng)(Underwater Vehicle-Manipulator System, UVMS)模型具有高度非線性、強耦合、水動力學參數(shù)變化等特點, 且其在作業(yè)過程受到復雜海洋多源干擾的作用, 這些都會嚴重影響UVMS 的操作和定位精度等指標[1]。因此, 有必要設計具有干擾抑制與補償能力的復合控制器, 以達到預期的抗擾等性能指標要求。

目前, UVMS 已經(jīng)有了較為成熟的建模與控制方法[2-4]。Fossen[2]采用牛頓-歐拉公式建立了UVMS 的模型, Tarn[3]提出了一種新的基于歐拉-朗格朗日方程和牛頓-歐拉公式的模型建立公式。這兩種經(jīng)典的建模方法為基于模型的控制奠定了基礎。Mahesh[4]研究了UVMS 的協(xié)調(diào)控制, 將水下機器人和機械臂系統(tǒng)的相互影響進行了系統(tǒng)性的闡述。隨著對控制精度要求的提高, 需要開發(fā)更加高效、精確的控制系統(tǒng), 在此基礎上許多學者提出了眾多新的控制方法[5]。Huang[6]結合干擾觀測器, 提出了基于模型的自適應控制; 針對UVMS 的動態(tài)不確定性和時變外部擾動, Dai[7]將擴張卡爾曼濾波器引入補償系統(tǒng), 將基于模型的力矩控制器與H∞魯棒補償跟蹤控制器結合設計了間接自適應控制器; Londhe[8]將單輸入模糊控制器應用于UVMS的軌跡跟蹤問題; Wang[9]采用離散延遲估計來處理未知的水動力干擾, 并針對UVMS 的閉環(huán)系統(tǒng)進行了分析。Huang[10]將運動學和動力學控制器相結合, 設計了基于動態(tài)模型的動力學控制器相結合, 設計了基于動態(tài)模型的自適應控制器, 提高了UVMS 操縱軌跡的精確性。這些方法都能達到較好的控制效果, 但是需要模型精確已知或者模型過于復雜。

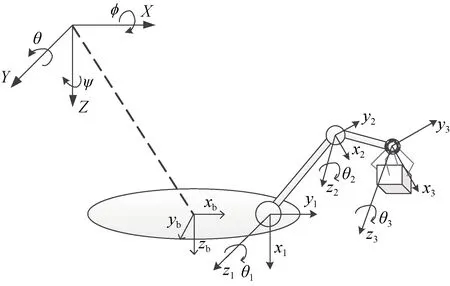
圖1 UVMS 的動態(tài)模型示意圖Fig. 1 Schematic of the dynamic model of UVMS

韓京清[11]借鑒PID 控制不依賴于模型的優(yōu)點,提出了自抗擾控制技術(Active Disturbance Rejection Control, ADRC)。其核心思想是將系統(tǒng)的內(nèi)部不確定性與外部擾動集總為“廣義總擾動”, 引入了非線性擴張狀態(tài)觀測器(Extended State Observer, ESO)對其進行估計; 并且在外部信號輸入端加入跟蹤微分器(Tracker Differential, TD)對輸入信號安排過渡過程,使得自抗擾控制具有快速的響應過程和良好的抗干擾能力[12-14]。但是其參數(shù)難以整定, 且非線性函數(shù)難以工業(yè)化的難點在很大程度上限制其工業(yè)應用。為了解決以上難點, Gao 等[15]用基于帶寬的思想提出了線性自抗擾控制器, 采用PD 控制器替換原來的非線性誤差反饋, 并將PD 控制器和線性擴張狀態(tài)觀測器(Linear Extended State Observer, LESO)的參數(shù)與其帶寬聯(lián)系起來, 提出了結構相對精簡的線性自抗擾控制器(Linear Active Disturbance Rejection Controller, LADRC), 該控制器極大減少了需要調(diào)節(jié)的參數(shù)。因此, LADRC 技術為具有多輸入多輸出的AUVMS 高精度控制設計帶來了可能。

本文針對UVMS, 將復雜系統(tǒng)模型轉變?yōu)楹唵蔚姆e分串聯(lián)系統(tǒng), 利用LESO 可對包括建模誤差、耦合、內(nèi)外部干擾、海洋多源干擾在內(nèi)的集總干擾進行估計并補償, 引入滑模控制器(Sliding Mode Control, SMC)增加系統(tǒng)的魯棒性, 建立了滑模自抗擾控制器(Sliding Mode Active Disturbance Rejection Control, SM-ADRC), 考慮用簡單的控制結構解決UVMS 的復雜控制問題, 最后仿真結果證明了該方法的有效性。首先建立了UVMS 的動力學模型, 將UVMS 分成6+n個子系統(tǒng), 針對每一個子系統(tǒng), 將內(nèi)部不確定性、外部干擾和其他子系統(tǒng)的耦合影響集總為總擾動, 設計LESO 進行估計, 再利用估計誤差建立滑模面, 給出UVMS 的SM-ADRC 設計方法,并進行 Lyapunov 穩(wěn)定性分析。在此基礎上得到UVMS 的SM-ADRC 設計方法, 并給出仿真結果, 與傳統(tǒng)LADRC 與SMC 的控制結果進行對比分析。

1 UVMS 動力學分析

1.1 UVMS 的動力學模型

作者將整個UVMS 系統(tǒng)視為剛體, 根據(jù)Fossen[2]的建模方法建立如下UVMS 動力學模型:

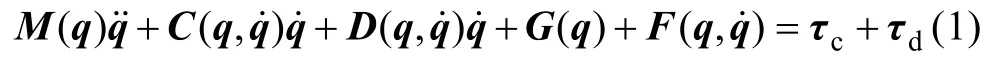
式中向量q= [X,Y,Z,φ,θ,Ψ,θ1,θ2, …,θn]T由船體的位置[X,Y,Z]T, 航向角[φ,θ,Ψ]T, 機械臂關節(jié)角度向量 [θ1,θ2, …,θn]T(n為機械臂關節(jié)個數(shù), 本文選取n=3), 因此系統(tǒng)總自由度為水下機器人本體的6 個自由度和機械臂關節(jié)的自由度之和, 即6+n。斜對稱正定矩陣M(q)是包括附加質(zhì)量的系統(tǒng)質(zhì)量矩陣, 為,C(q,)表示包括附加質(zhì)量的科氏力和向心力部分[15],D(q,)表示水動力阻尼部分,G(q)表示船體的浮力與重力之間的總和作用,F(q,)表示系統(tǒng)中水下機器人與機械臂相對運動間的耦合影響,τc是整個系統(tǒng)的控制輸入,τd為難以測量的未知擾動。根據(jù)UVMS的固有特征, 系統(tǒng)(1)中的系數(shù)矩陣有以下特性[16-19]:

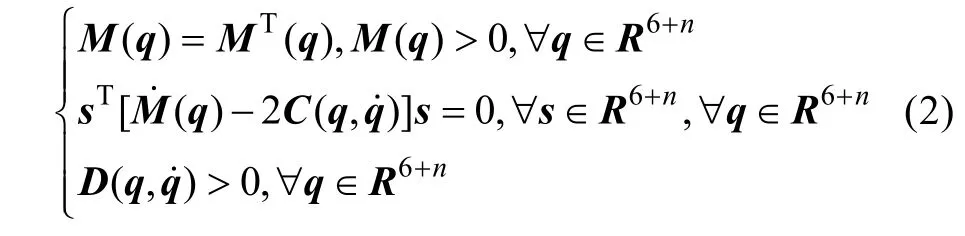
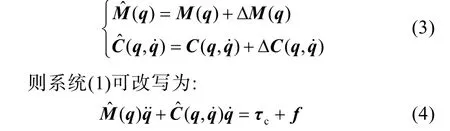
式中f為建模誤差, 參數(shù)不確定性, 水動力阻尼影響和未知干擾等的總和, 即:

定義系統(tǒng)維數(shù)為m= 6+n, 因此系統(tǒng)模型(4)可展開為:

其中系數(shù)矩陣[aii]m×m(q)和[cii]m×m(q,q˙ ),y=q為系統(tǒng)輸出向量,u=τc為系統(tǒng)控制輸入向量,f為總擾動向量。

圖1 給出UVMS 的動態(tài)模型示意圖, 定義圖中坐標軸Ie(X,Y,Z)為慣性坐標系,Ib(xb,yb,zb)為機身坐標系,Ii(xi,yi,zi),i=1, 2, …,n為機械臂關節(jié)自身坐標系, 其中n為機械臂關節(jié)個數(shù), 本文只考慮機械臂關節(jié)繞Z軸旋轉。

1.2 水動力參數(shù)分析

假設UVMS 的構成為圓柱體, 則其在水下所受的黏性曳力動力學模型為[20]:

式中vr為被控對象與洋流的相對速度,ρ為水密度(海水密度為1.02～1.07),Ds為線性表面摩擦系數(shù),Dsvr即為線性表面摩擦力。A(α)為被示性曲面前部的投影橫截面積,α為沖角。ο ()為階數(shù)大于等于三階的高階相, 通常可忽略。Cd(Rn,α)為曳引系數(shù), 由雷諾數(shù)Rn決定。而雷諾系數(shù)可以由以下公式求得:

式中d是垂直于流體速度vb方向的物體的特征長度,μ為流體黏性系數(shù)。

升力垂直于流動方向。對于水下運動物體, 它們可以被建模為[20]:

式中Cl為升力系數(shù), 由雷諾系數(shù)與沖角決定。表1給出了圓柱體雷諾數(shù)函數(shù)的升力系數(shù)與曳力系數(shù)。

表1 UVMS 的升曳系數(shù)Tab. 1 Drag force and lift force of the UVMS

當剛體在重力作用下浸入流體中時, 必須考慮兩個主要的力: 重力和浮力。后者是唯一的流體靜力學效應, 它不是機身和液體之間相對運動的函數(shù)。

定義如下向量:

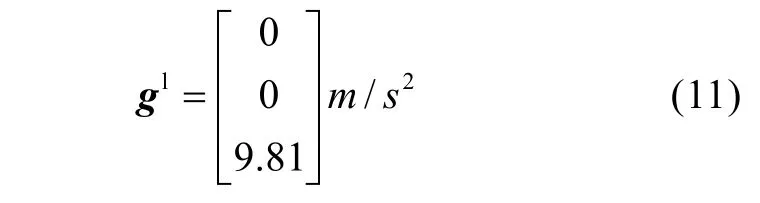
為重力加速度向量,V為機身的體積,m為質(zhì)量。則物體浮重為W=, 所受浮力為B=。作用在機身的重心=[xG,yG,zG]的重力在機身坐標系可表示為:

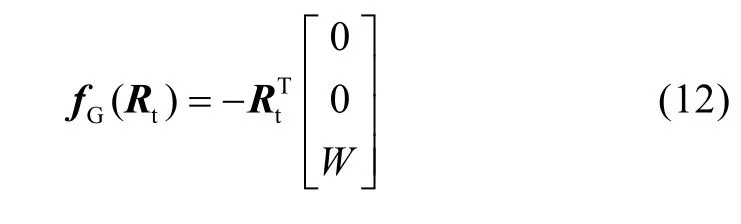
式中Rt為轉移矩陣, 作用于浮心=[xB,yB,zB]的浮力在機身坐標系可表示為:

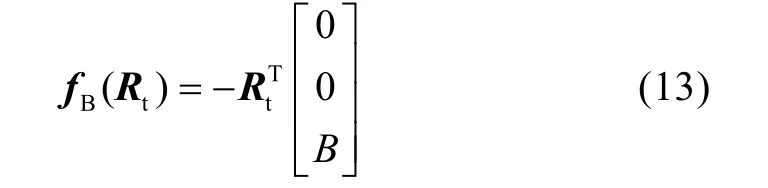
因此在機身坐標系內(nèi)的重力和浮力作用下的力/力矩矢量可表示為:

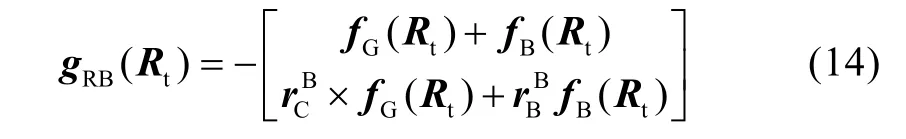
由于假設重力作用在剛體上是一致的, 所以質(zhì)心和重心是重合的。

用歐拉角可以將gRB表示為:

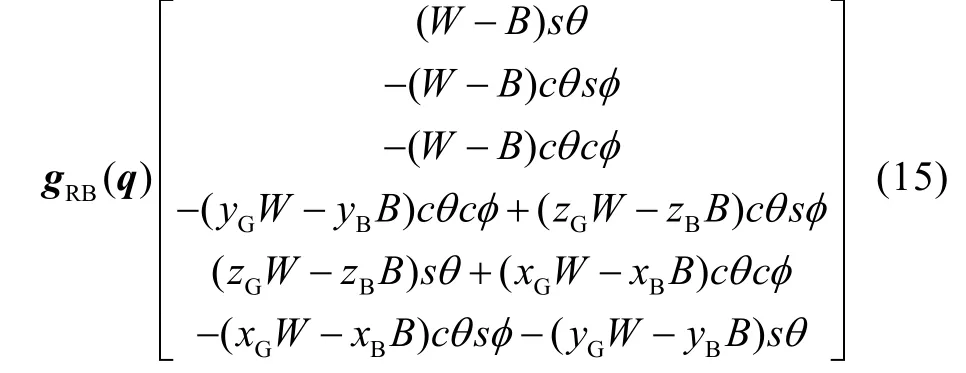
式中s(.)和c(.)表示正弦與余弦函數(shù)。

當一個剛體在流體中運動時, 必須考慮圍繞著它的流體的附加慣性, 也就是由于流體的運動而加速的慣性。這種效應在工業(yè)機器人中可以忽略, 因為空氣的密度比移動機械系統(tǒng)的密度輕得多。然而在水下時水下機器人的密度相比, 水的密度ρ≈1 000 kg/m3。在0 度時凈水密度為1 002.68 kg/m3; 含鹽量為3.5%的海水密度為1 028.48 kg/m3。

當物體具有一定速度地通過流體時, 在物體的支撐下, 周圍的流體也會加速。因此, 會產(chǎn)生方向相反的力施加在物體上, 即附加質(zhì)量力, 它可以由為一個6×6 的矩陣表示。由于附加質(zhì)量是物體表面幾何形狀的函數(shù), 所以對于剛體的6×6 慣性矩陣, 其性質(zhì)各不相同。例如慣性矩陣不一定是正定的。

以沿xb方向的線性加速度所產(chǎn)生的水動力為例,定義:

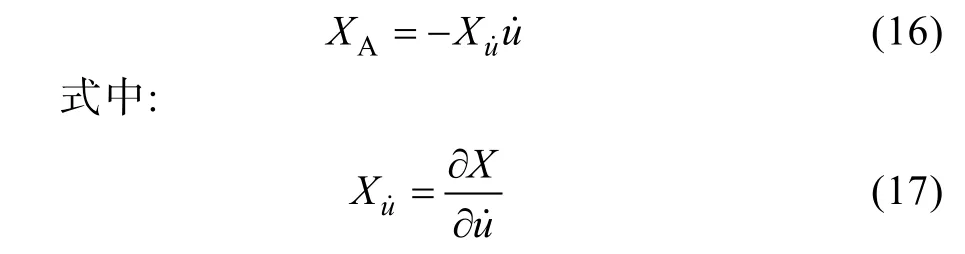
同樣地, 可定義所有與6 個力/力矩分量[X,Y, Z,K,M,N]T和6 個線性/角加速度相關的其余元素, 這些元素可以被分組到附加的質(zhì)量矩陣MA中。對于完全浸入水中的物體則有MA>0, 并且對于理想液體(無雜物), 物體移速較慢且無海浪或洋流時有[21]:

附加質(zhì)量也增加了科氏力和向心力, 可以用矩陣表示為:

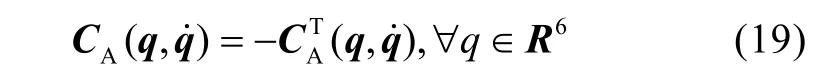
物體完全浸入水中, 運動速度較低, 且具有水下航行器常見的3 個對稱面, 則可以考慮以下矩陣MA和CA的結構:

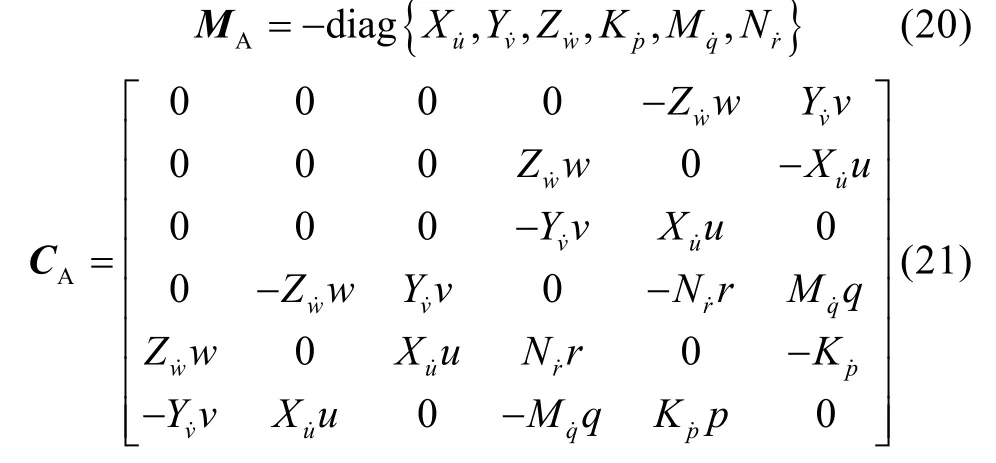
其中[u,v,w]與[p,q,r]分別對應船體的位置[X,Y,Z]與航向角[φ,θ,Ψ]方向上的速度。

對于質(zhì)量為m, 長度為L, 截面半徑為r的圓柱形剛體, 其附加質(zhì)量系數(shù)可選取為:

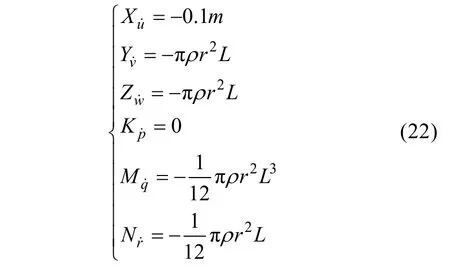
在[20]中可以找到關于圓柱在流體中運動的附加質(zhì)量效應的詳細的理論和實驗討論, 它表明附加質(zhì)量矩陣是狀態(tài)相關的, 它的系數(shù)是圓柱運動距離的函數(shù)。

流體的黏度也會對物體產(chǎn)生耗散阻力和升力,即為式(1)中的D（q,q˙）q˙ 項。一種常見的簡化方法是只考慮線性和二次阻尼項, 并將這些項組合成一個矩陣D（q,q˙ ）, 并有:

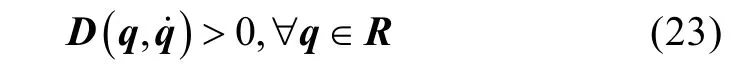
這個矩陣的系數(shù)也被認為是常數(shù)。對于完全浸入水中的物體, 可以做以下進一步的假設

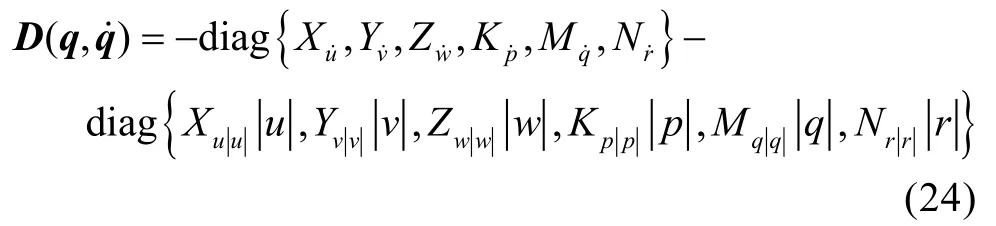
需要注意的是當假定阻尼矩陣為對角結構時就意味著忽略耦合耗散項。

2 滑模自抗擾控制器

系統(tǒng)(7)是一個高維不確定系統(tǒng)。為了方便進行控制設計, 根據(jù)其具體維數(shù)將UVMS 分成m個子系統(tǒng), 針對每一個子系統(tǒng), 將建模誤差, 外部干擾和其他子系統(tǒng)的耦合影響等集總為總擾動, 設計LESO進行估計, 再利用估計誤差建立滑模面, 構造滑模控制器。在此基礎上得到針對整個 UVMS 的SM-ADRC 設計方法。

2.1 線性擴張觀測器

以系統(tǒng)(7)中的第一個子系統(tǒng)為例:

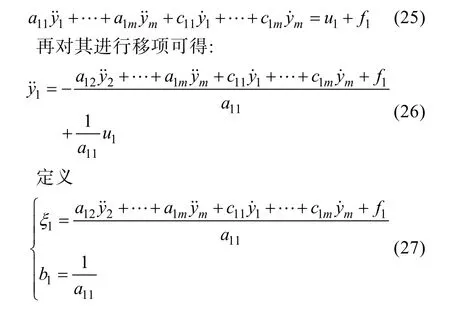
式中為ξ1子系統(tǒng)(25)的廣義總擾動, 包含了內(nèi)部的不確定性和外部未知干擾, 假設其未知但有界。則系統(tǒng)(26)可重新寫作:

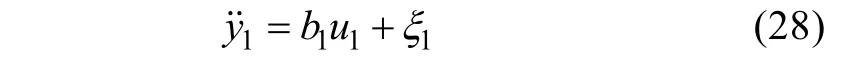
現(xiàn)將總擾動ξ1擴展為系統(tǒng)的狀態(tài)變量x3= ξ1,同時假設其微分有界, 并定義=w, 則可以列出所對應的二階系統(tǒng)的狀態(tài)空間表達式:

基于狀態(tài)方程(29)可以建立如下觀測器:

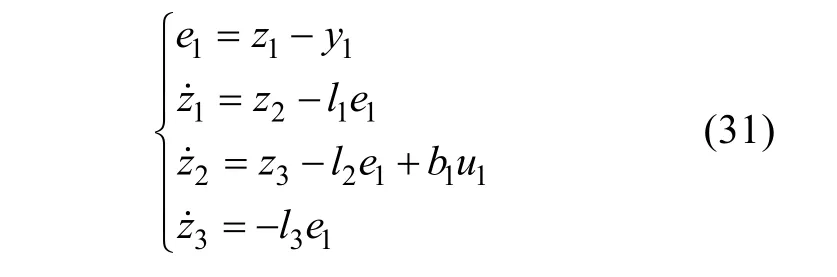
式中l(wèi)1,l2,l3為觀測器增益, 加入擴張狀態(tài)量的觀測器(31)稱為LESO。若觀測器增益選為:

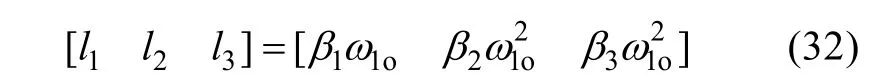
可使得s3+β1s2+β2s+β3滿足Hurwitz 條件。而且可以通過改變β來調(diào)整特征根的位置[13], 如將其配置于s3+ β1s2+ β2s+ β3= (s+ ω1o)3, 則有:

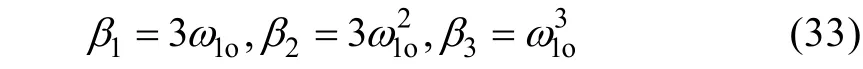
式中ω1o為第一個子系統(tǒng)的LESO 的觀測器帶寬。

2.2 LESO 收斂性及估計誤差分析

將(31)中觀測器增益取為(33)中對應值, 在做拉氏變換, 可以求得狀態(tài)變量的估計值z1,z2,z3的傳遞函數(shù):

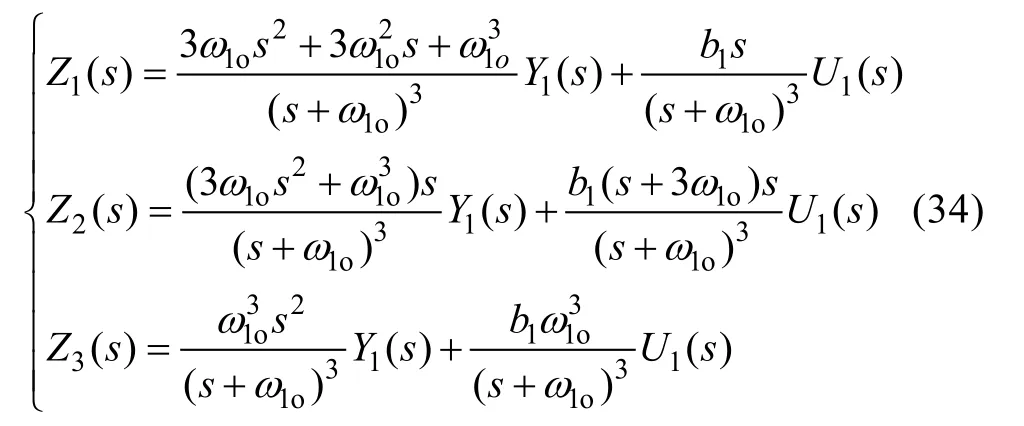
定義觀測器跟蹤誤差為:

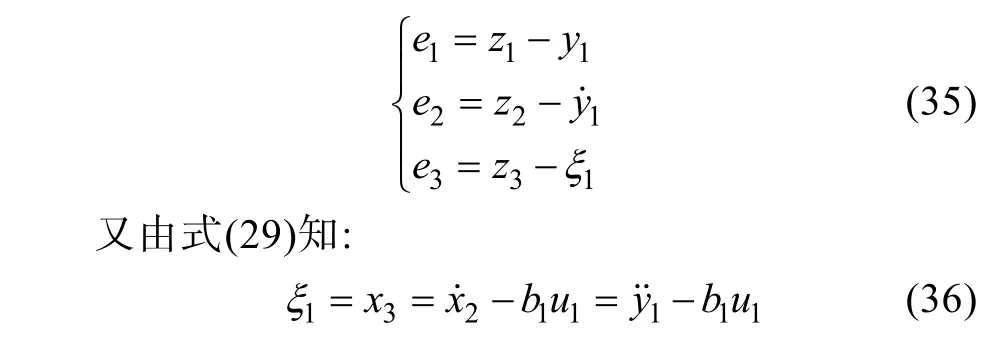
因此可以解出誤差的傳遞函數(shù):

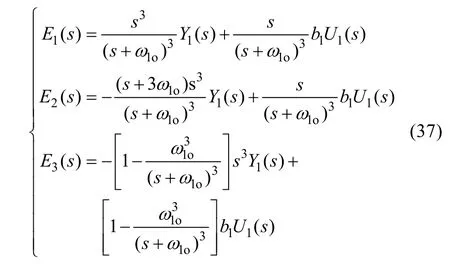
一般性地將式(37)中輸入輸出Y1(s),U1(s)取為幅值為K的階躍信號即Y1(s)=K/s,U1(s)=K/s來對系統(tǒng)的穩(wěn)態(tài)進行分析, 則可求得穩(wěn)態(tài)誤差為:

再考慮LESO 的估計誤差的動態(tài)特性。由(30)和(31)可得LESO 對系統(tǒng)(9)的跟蹤誤差方程:

假設作用于此系統(tǒng)的擾動有界, 定義式(39)的狀態(tài)轉移為[22]:

其中，e= [e1,e2,e3]T,η= [η1,η2,η3]T,Λ= diag[,1]T。將(41)代入(39)可得:

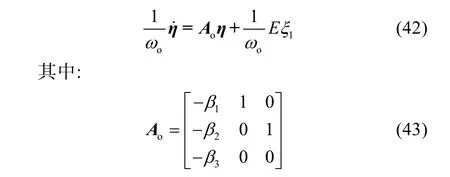
通過2.1 節(jié)的配置已使得Ao的特征值均具有負實部:

因此由式(42)不難得出當ω1o增大時總擾動項ξ1的影響會隨之減小, 且LESO 的跟蹤誤差逐漸減小。

2.3 子系統(tǒng)的滑模變結構控制器

引理1[23]對于V:[0,∞)∈R不等式:

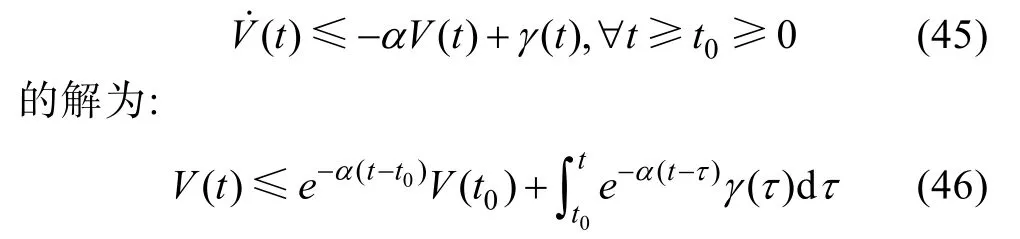
同樣以UVMS 的第一個子系統(tǒng)為例, 并基于上節(jié)所述的總擾動項有:

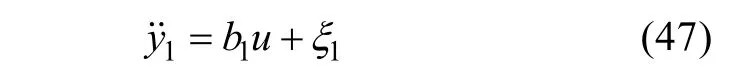
定義系統(tǒng)期望輸出為y1d, 且假設y1d有界。LESO 估計誤差為:-y1d, 定義滑模面為:

式中c>0。

基于LESO(31)可建立如下滑模控制器:

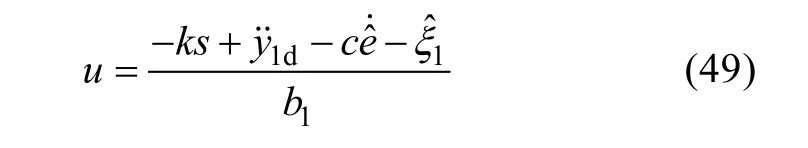
針對系統(tǒng)(47), 選擇自抗擾滑模控制器(48)、(49)中的參數(shù)k>1/2, 則其閉環(huán)系統(tǒng)的跟蹤誤差將收斂至某鄰域, 且其收斂速度與LESO 的參數(shù)ωo和k有關。

證明:

引入Lyapunov 函數(shù):

由引理1 可解得:

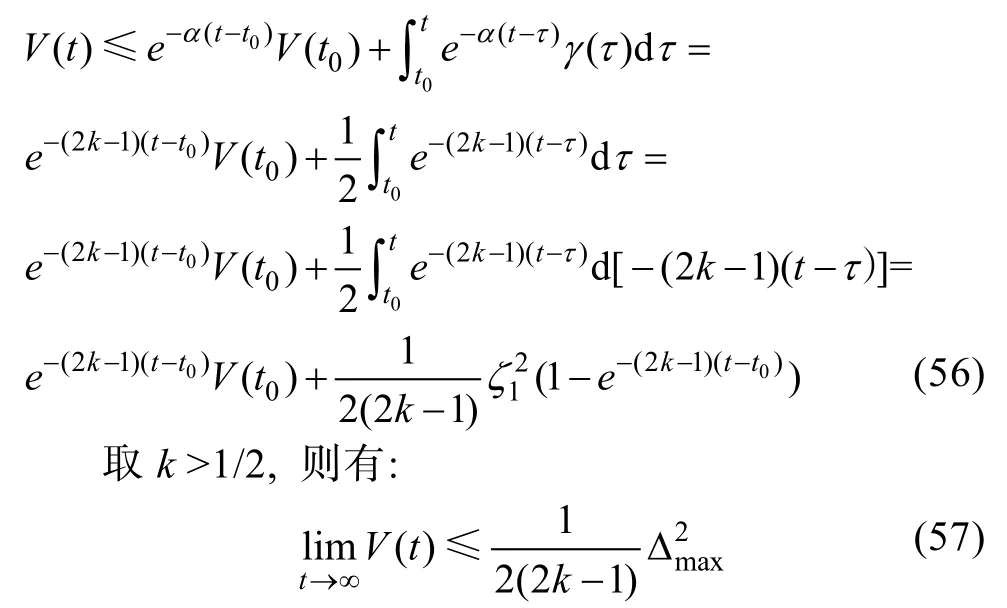
由于V(t) =s2>0, 所以當t→∞有:

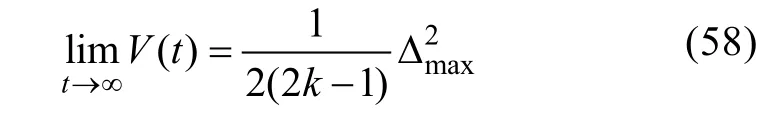
可以看到當LESO 對擾動的跟蹤誤差逼近于0,k足夠大時:

因此當k>1/2 時跟蹤誤差e? 逐漸收斂到鄰域D= ｛≤ φ｝且其收斂速度取決于LESO 增益ωo和滑模控制器增益k。

由以上可知系統(tǒng)的穩(wěn)定性與收斂速度由滑模參數(shù)k和觀測器參數(shù)ωo決定。其余子系統(tǒng)的控制器及其穩(wěn)定性可由同樣的方法建立與驗證。

2.4 微分跟蹤器設計

考慮當輸入信號為非光滑信號時, 避免出現(xiàn)數(shù)字計算中的高頻振蕩, 和為狀態(tài)變量的提取安排過渡過程, 采用積分鏈式微分器提取輸入信號的微分,通過每層的積分環(huán)節(jié)對擾動進行抑制。該有限時間收斂二階階微分器(TD)為:

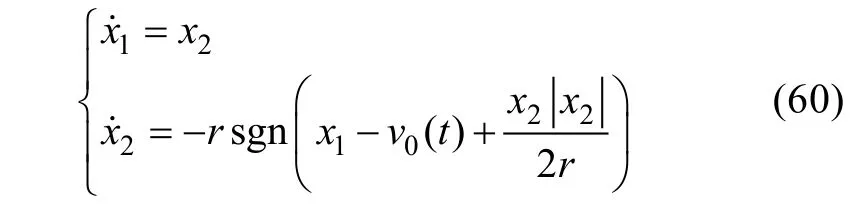
式中v0(t)為輸入信號, 狀態(tài)量x1在加速度的限制≤r之下, 能快速的跟蹤輸入信號v0(t), 且r越大,其跟蹤速度越快, 同樣當x1充分的接近v0(t)時, 另一狀態(tài)量x2(t) =x˙1(t)可作為輸入信號的近似微分。

2.5 UVMS 的SM-ADRC 設計

綜上, 完整的滑模自抗擾控制結構圖由圖2 給出,圖中yd1與yd2分別為參考輸入的跟蹤信號與其微分信號。其他8 個子系統(tǒng)可以以同樣的方法建立控制器, 針對AUVMS 的完整SM-ADRC 的結構圖如圖3 所示。

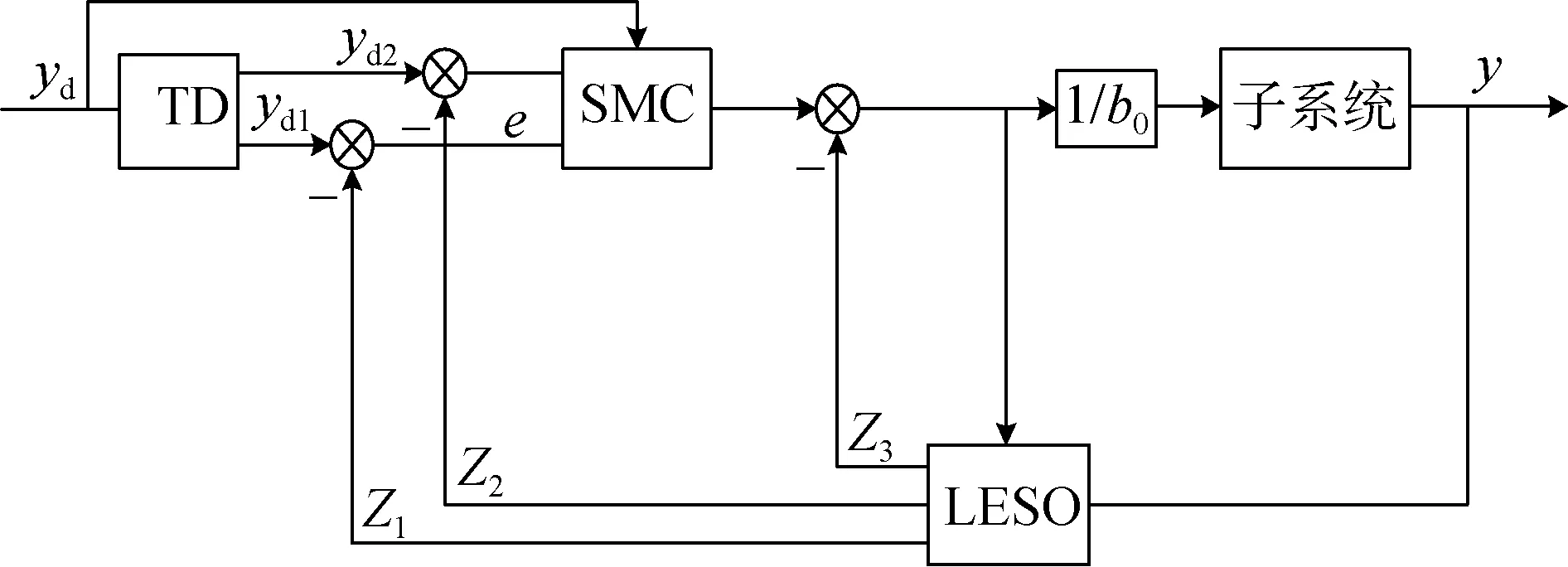
圖2 SM-ADRC 結構圖Fig. 2 Structure of SM-ADRC

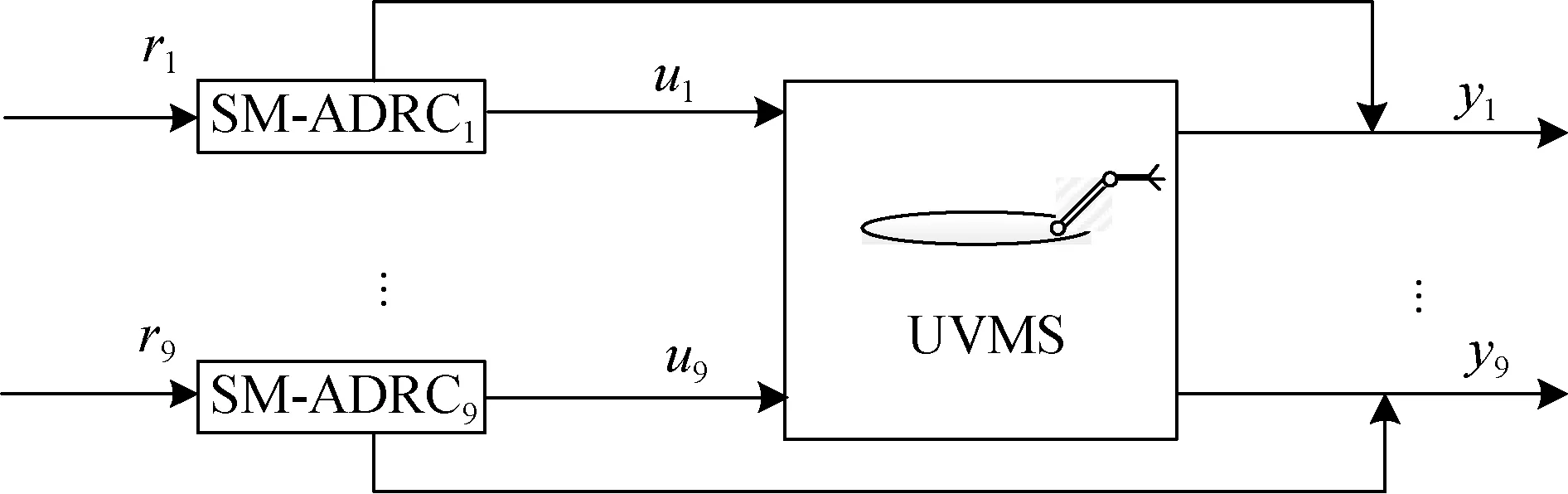
圖3 UVMS 的SM-ADRC 結構圖Fig. 3 Frame of SM-ADRC for UVMS

3 仿真結果與分析

基于UVMS 的工作特點, 在本節(jié)對帶有兩連桿(連接關節(jié)n=3)的UVMS 的航行軌跡, 機械臂旋轉軌跡進行跟蹤實驗, 測驗控制器對UVMS 的航向角切換頻率要求。并且將實驗結果與傳統(tǒng)滑模控制, 自抗擾控制進行對比。

在仿真實驗中, 9 個子系統(tǒng)的LESO 的參數(shù)分別為ωo=[150, 80, 135, 420, 556, 894, 240, 779, 368]。微分跟蹤器參數(shù)r均在集合[20, 30]取值 , 滑模控制器中參數(shù)c在集合[2, 3]中取值, 參數(shù)k=[45, 36, 22, 44,59, 71, 46, 59, 88] 對應每個子系統(tǒng)。定義UVMS 的初始位置為原點, 即[X, Y, Z] =[0, 0, 0]。為了驗證控制器對位置的快速變化的跟蹤能力, 將UVMS 的機械臂關節(jié)角度在0 到5 秒內(nèi)期望角度變化軌跡設定為:

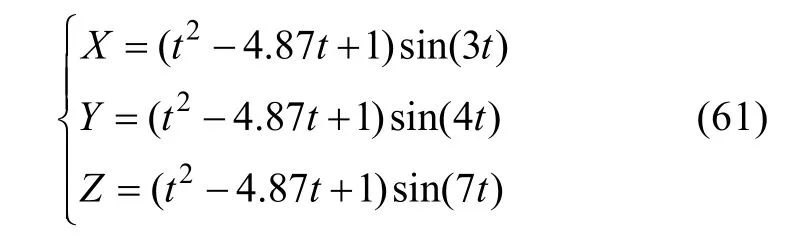
并同時考慮UVMS 的位置快速變化時的跟蹤效果和航向角變化狀態(tài)。為了使仿真效果盡可能的接近水下環(huán)境, 作者將外部干擾設計為一階高斯-馬爾科夫模型來模擬洋流的運動學特征。其表達式如下:

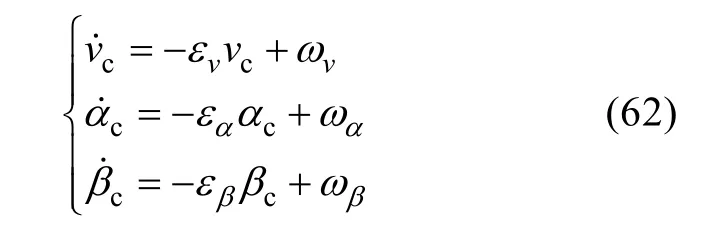
式中vc為設定的洋流速度,αc和βc為洋流的運動方向,εc、εα和εβ為較小的正實數(shù),ωv、ωα和ωβ分別為不同頻率的高斯白噪聲。

在圖4 和圖5 中可以看到, 滑模自抗擾控制器可以很好地避免傳統(tǒng)滑模控制的抖振現(xiàn)象, 實現(xiàn)更精確的跟蹤軌跡, 并且在位置陡然變化時能較傳統(tǒng)線性自抗擾控制器和滑模控制器更快的跟蹤位置變化,有更平穩(wěn)快速的響應過程, 圖5 中[Ex,Ey,Ez]分別指代對UVMS 的位置[X,Y,Z]的跟蹤誤差。在圖6 中可以看到3 個控制器都能跟蹤機械臂的擺動角度軌跡進行但在圖7 中, [Eθ1,Eθ2,Eθ3]分別對應在各個控制器的控制下關節(jié)角的跟蹤誤差, 從中可以看出, 機械臂關節(jié)角度軌跡跟蹤結果顯示滑模自抗擾控制器能更快更精準地跟蹤機械臂擺動的軌跡, 在不同工況(機械臂不同的擺動頻率)下均能達到非常良好的軌跡跟蹤效果, 跟蹤誤差小于LADRC 與SMC, 顯示了SM-ADRC 優(yōu)良的魯棒性。為了公平地驗證所設計的控制的控制效果, 在仿真中3 個控制器的所產(chǎn)生的控制輸入在圖8 給出, 控制輸入的消耗在一定程度上可以反映控制對能量的消耗, 如電機的耗電量。在圖8 中可以看到與傳統(tǒng)滑模控制與LADRC 相比, 要達到圖 4～圖7 的控制效果, 文中所設計的SM-ADRC所許需的控制輸入量是最少的, 這說明了SM-ADRC 可以依靠更小的能量消耗而達到更好的控制效果, 具有更高的工業(yè)化的能力。

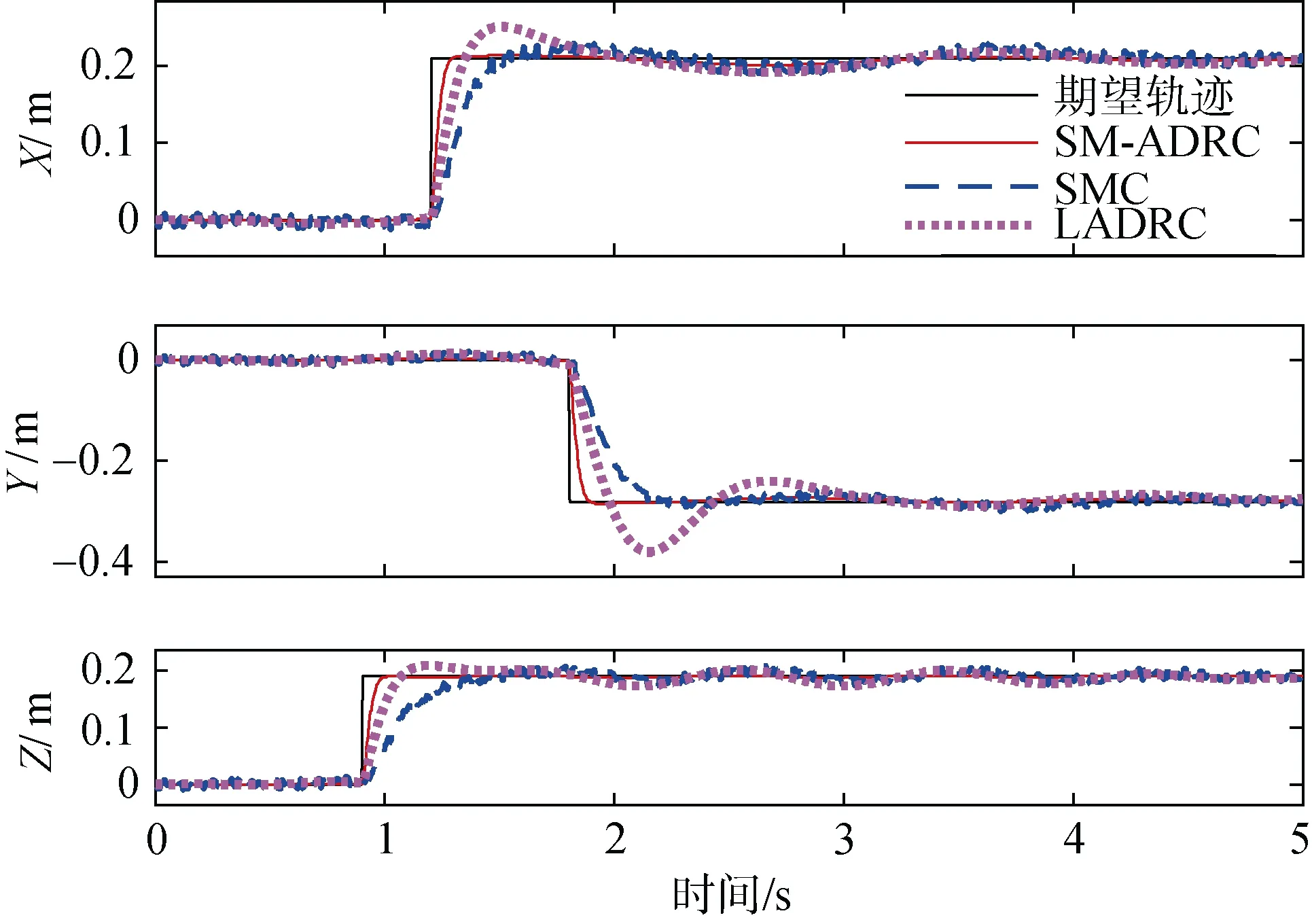
圖4 UVMS 位置變化軌跡Fig. 4 Trajectory of UVMS’s position

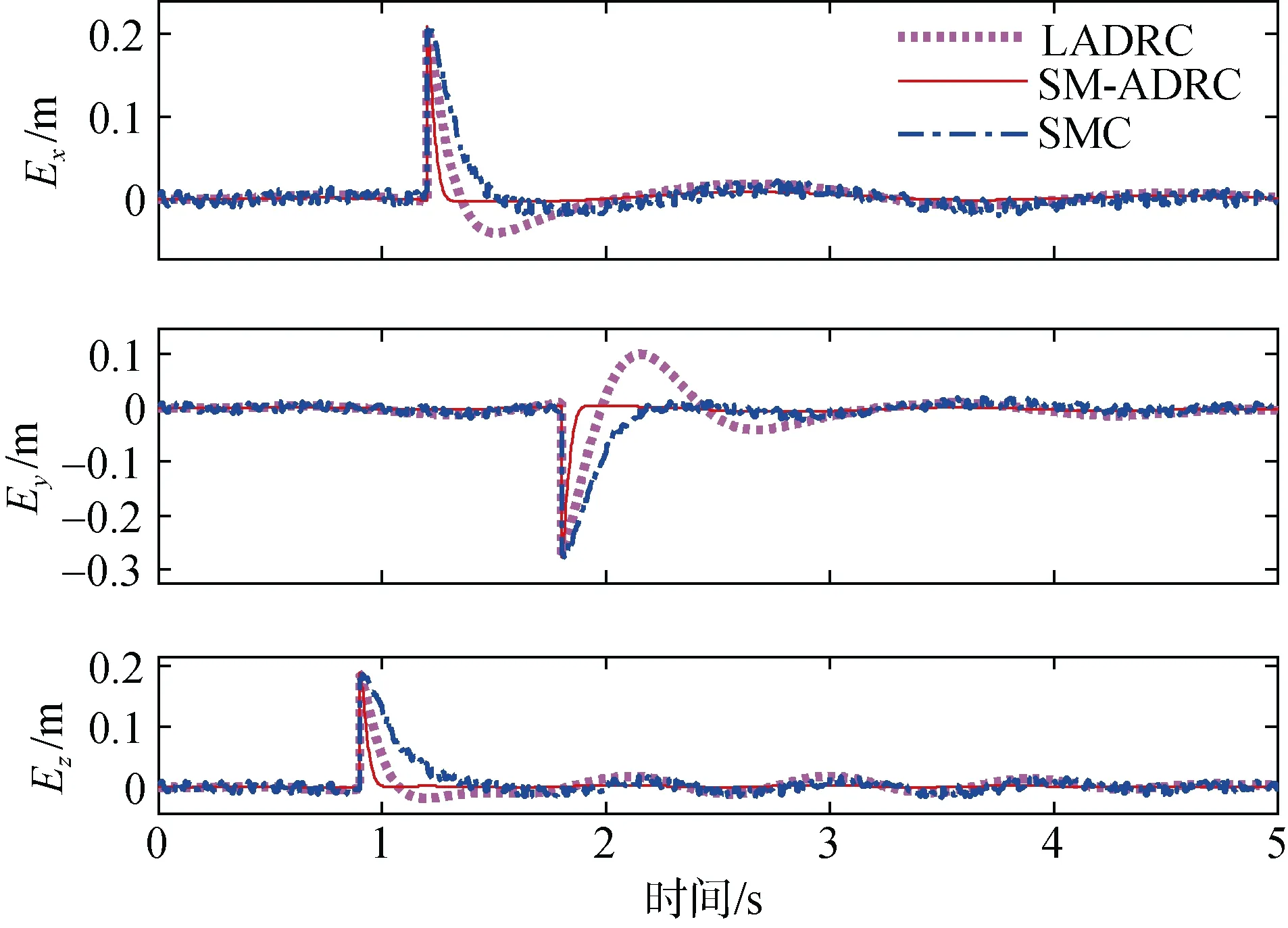
圖5 UVMS 位置跟蹤誤差Fig. 5 Error in the UVMS’s position tracking

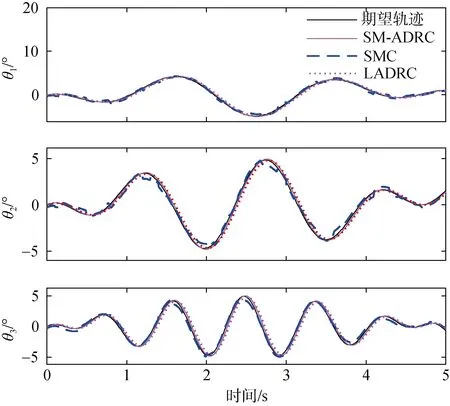
圖6 機械臂關節(jié)角度軌跡跟蹤結果Fig. 6 Angular trajectory tracking of manipulators

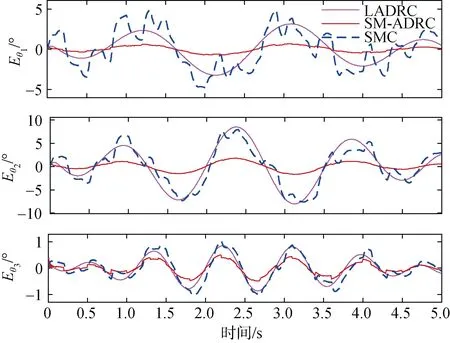
圖7 UVMS 機械臂期望關節(jié)角軌跡的跟蹤誤差Fig. 7 Error in tracking the UVMS manipulator angular Trajectory

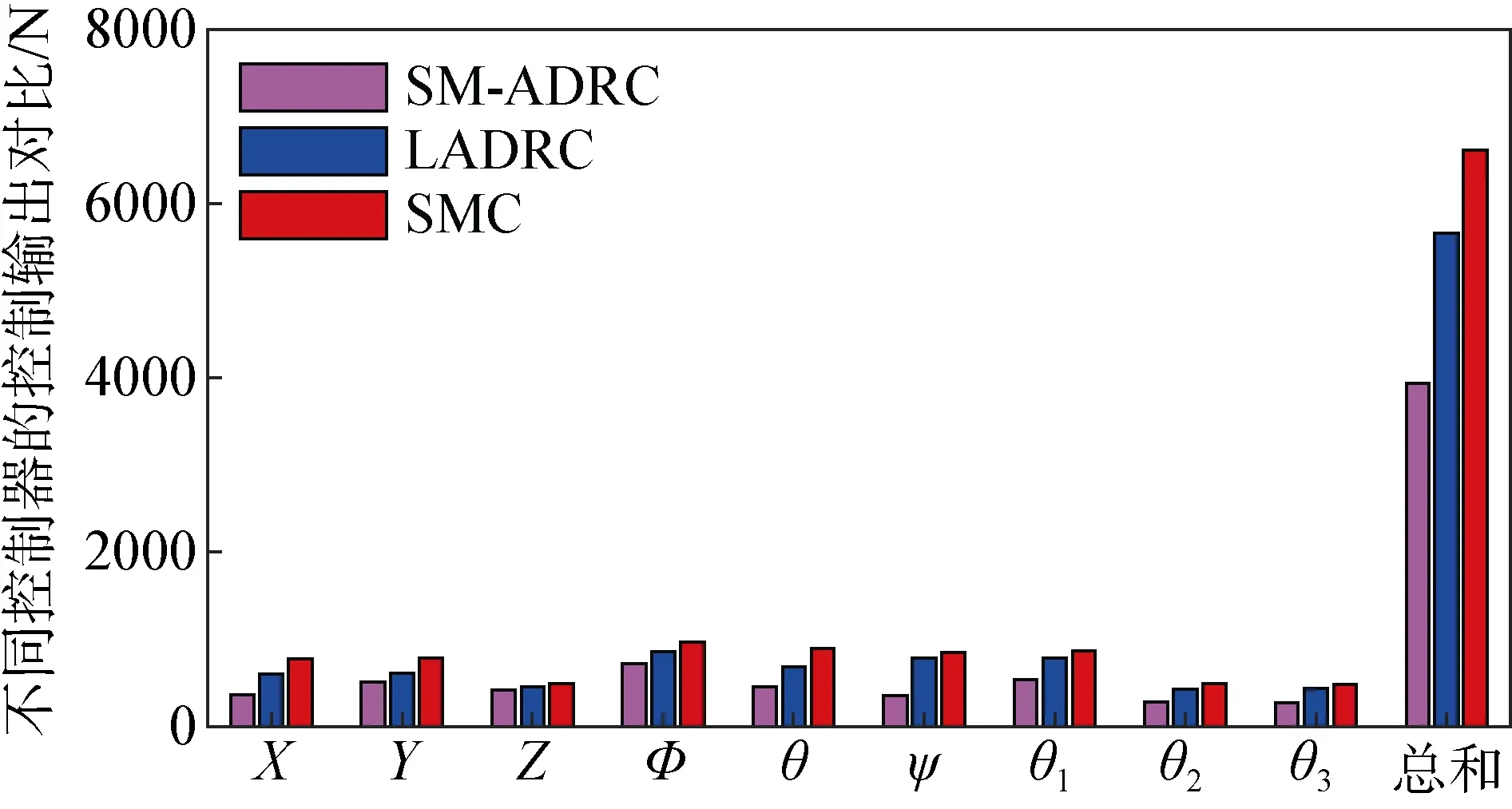
圖8 不同控制器的控制輸出對比Fig. 8 Comparison of the control outputs of three controllers

4 結論

作者提出的滑模自抗擾控制器具有良好的響應過程, 并通過線性擴張觀測器對擾動的實時估計,很大程度上消除了傳統(tǒng)滑模控制器的抖振現(xiàn)象。通過滑模控制器代替?zhèn)鹘y(tǒng)線性自抗擾控制器中的PD控制器, 在系統(tǒng)輸入信號快速切換時能保持整個系統(tǒng)的穩(wěn)定, 并且控制過程中的超調(diào)現(xiàn)象大幅度減小,此外, 作者所設計的控制器與傳統(tǒng)滑模控制器和線性自抗擾控制器相比能用更少的控制量達到更好的控制效果, 這在一定程度上保證了所設計的控制器的可進行實際工業(yè)化。最后通過仿真實驗驗證了提出的控制器有效性。