基于分布式魯棒機會約束的中歐班列空箱調運優化

邢 磊，靳志宏，王小寒，蔡佳芯

(大連海事大學 交通運輸工程學院， 遼寧 大連 116026)

2013年，中國為促進經濟發展，提出“一帶一路”倡議，極大促進了中歐貿易往來。截至2019年1月，中歐班列累計開行12 000列，涵蓋了中國56個城市以及歐洲49個城市。由于中歐貿易的不平衡性，東向班列(開往中國)開行數目大約為西向班列(開往歐洲)開行數目的一半[1]。這導致中國城市成為空箱需求點，歐洲城市成為空箱供給點，降低空箱回程成本成為現實運營中的一大難點。中歐班列開通前，中歐之間90%的貨物都以海上運輸為主，運輸時間大約為30～40 d。中歐班列開通后，貨物的運輸時間縮短至20～30 d。但是，中歐班列的運輸成本大約為海上運輸的4倍。為了維持中歐班列的健康運行，中國政府實行了補貼政策，使得實際運輸成本與海上運輸成本相差不大。然而到2020年，政府將逐漸收回補貼政策，這勢必導致部分城市空箱需求量發生變化，為空箱調運增加了不確定因素。當前，為減少空箱調運成本，部分空箱通過海陸聯運的方式調回，但增加了運輸時間。與此同時，可折疊集裝箱的出現也為減少空箱調運成本帶來一定的可能性。

近年來，一些國內外學者對不確定環境下空箱調運問題進行了研究。韓曉龍等[2]構建了含有概率約束規劃的多目標空箱調運優化模型，將概率模型轉化為確定性整數規劃模型后求解。蔡佩林等[3]構建了隨機需求下3種港口集裝箱空箱調運博弈模型，論證了不同調度策略對3種模型的影響。趙雅琦等[4]構建了考慮可折疊集裝箱的機會約束規劃空箱調運優化模型，分析了可折疊集裝箱實現空箱調運成本降低的潛在可能性。陳繼紅等[5]構建了班輪聯盟下的空重箱艙位租賃分配隨機機會約束規劃模型，并將模型轉化為確定性規劃模型求解。肖青等[6]考慮重箱需求模糊性對空箱調運的影響，構建了空箱調運模糊規劃模型，并轉化為確定性的等價形式求解。徐奇等[7]構建了多周期下的多式聯運空重箱聯合調度隨機規劃模型，采用動態規劃與遺傳算法聯合的方法求解。汪傳旭等[8]構建了船公司合作下的多港口空箱調運優化模型，引入港口空箱配對轉運思想，并驗證了該思想在解決空箱調運模型上的有效性。江玉杰等[9]構建了船公司合作下的海運空箱調運模糊優化模型，算例結果表明合作調箱策略能夠降低總成本。 Long等[10]構建了兩階段隨機規劃空箱調運模型，并采用樣本平均值近似方法估計預期成本函數，設計了基于漸進式對沖策略的算法來解決樣本平均值近似問題。Song等[11]基于海港的動態信息，采用離散時間規劃方法構建空箱調運優化模型，設計了價值迭代算法來評估不同方案的最優策略。Hosseini等[12]構建了一種新的輔助機會約束規劃空箱調運優化模型，并通過證明將其轉換為確定性約束規劃模型。Francesco等[13]構建了基于時間擴展的多場景空箱調運優化模型，通過算例驗證由于參數的不確定導致用來滿足不同場景下的空箱需求值可能不同。Erera等[14]提出了一種基于時空網絡的魯棒性優化方法來解決動態空箱調運優化模型，驗證了魯棒性優化方法在一定情形下能夠有效恢復網絡中由于供需不確定性導致的流量失衡。

綜上所述，既有研究多以單一運輸方式的空箱調運優化為主，缺乏海陸聯運方面的研究，而且大多假設空箱需求的概率分布事先已知。但是，中歐班列開通年限較短，歷史數據較少，導致空箱需求的概率分布難以確定。本文采用分布式魯棒優化的方法，考慮回程可采用陸上、海陸聯運兩種方式以及可折疊集裝箱因素的影響，對中歐班列的空箱調運優化問題進行研究。

1 問題描述

當貨源客戶產生空箱需求時，班列公司為其提供空箱服務。在每個時期內，班列公司的空箱供給主要來源于該時期內的重箱轉化以及從其他城市調運的空箱。若貨源客戶的空箱需求量大于班列公司的供給量，班列公司需向租箱公司租用箱子，從而滿足貨源客戶的空箱需求，完成運輸后在本時期末還給租箱公司。若貨源客戶的空箱需求量小于班列公司的供給量，班列公司則會將多余的空箱堆存在集裝箱場站，并向集裝箱場站支付堆存費用。由于貨源客戶存在較大的隨機性，并且容易受國家政策影響，各城市每個周期內的部分空箱需求客戶處于變化之中。考慮到中歐班列開通年限較短，歷史數據較少，難以掌握不確定性需求客戶在每個周期空箱需求量的精確值或概率分布，引入分布式魯棒優化原理，基于不確定需求量的部分信息，研究中歐班列的空箱調運優化問題。該問題主要有以下3個特性：

(1)部分空箱調運可考慮海陸聯運，雖能夠極大地降低運輸成本，但增加了運輸時間。如何兼顧成本與時間選擇運輸方式是中歐班列空箱調運的優化方向。

(2)多個可折疊集裝箱能夠折疊成一個標準集裝箱，從而降低空箱調運的運輸成本，但額外增加了折疊、展開成本。同時，可折疊集裝箱的租用成本也高于標準集裝箱。通過靈敏度分析探究使用可折疊集裝箱降低空箱調運總成本的潛在可能性也成為中歐班列空箱調運優化問題的一大特點。

(3)不確定客戶節點需求決定了該問題帶有隨機性。考慮需求分布的不確定性，引入分布式魯棒優化理論，假設空箱需求的概率分布為一個分布集，分布式魯棒優化與機會約束相結合，以最壞情況下的優化為基礎，得到具有魯棒性的優化方案，即該優化方案受參數變化擾動不敏感。

當前中歐班列的運行模式為“點對點”形式，開通方向分為單向、雙向兩種，見圖1。同一區域內節點間(中國或歐洲)空箱調運可選擇公、鐵、海3種運輸方式，見圖1(a)。跨區域中歐節點間空箱調運可選擇班列運輸以及海陸聯運方式運輸，見圖1(b)、圖1(c)。

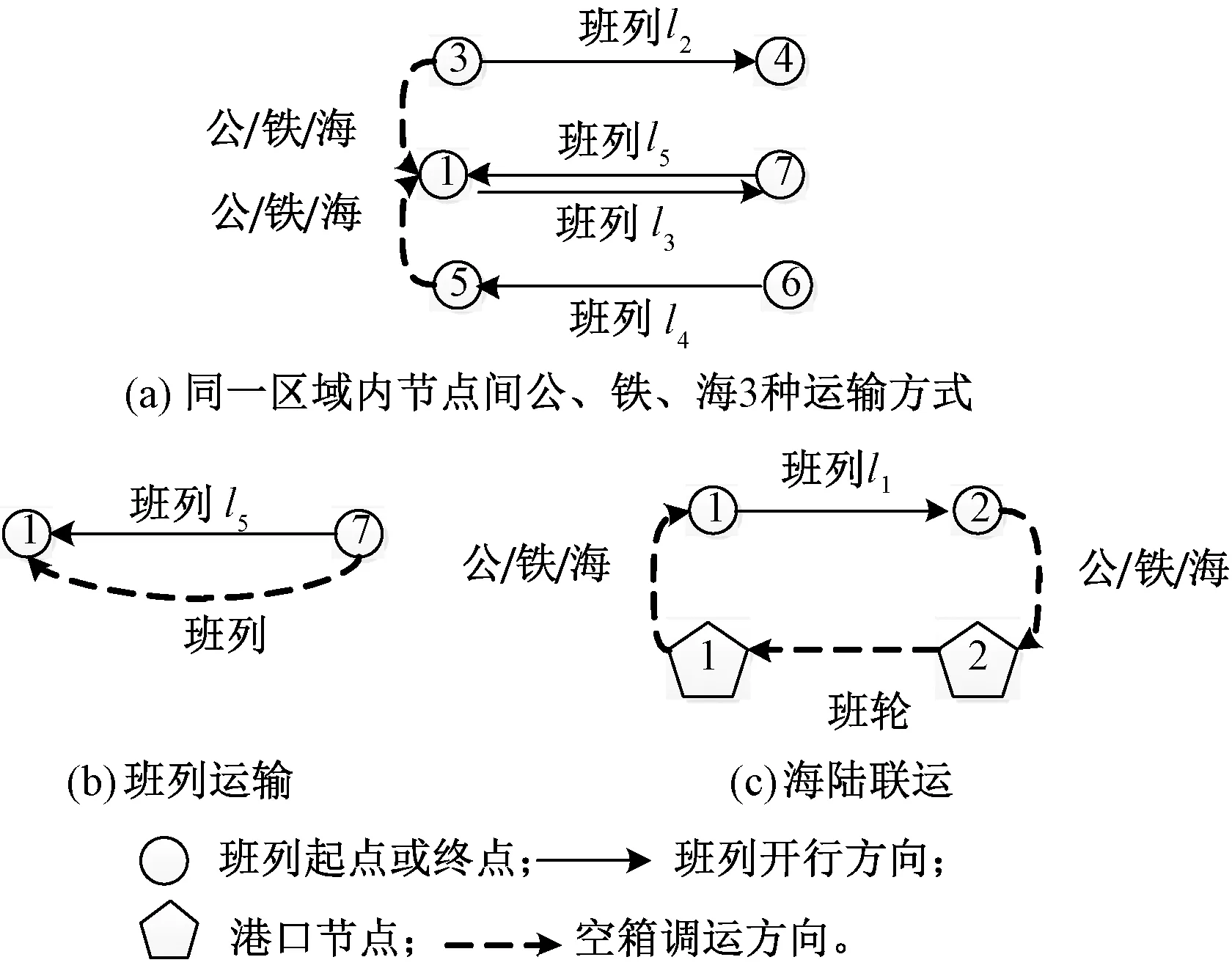
圖1 中歐班列空箱調運運輸方式選擇示意圖

基于問題的3個特性以及中歐班列運行特點，研究多周期下的中歐班列空箱調運優化問題，可簡化為不確定環境下的多城市多種運輸方式的空箱調運問題，旨在降低班列公司空箱調運的總成本。

2 分布式魯棒機會約束中歐班列空箱調運優化模型構建

2.1 基本假設

(1)班列的開行線路已知，各節點間的運輸方式、運輸時間和單位運輸成本已知。

(2)可折疊集裝箱在運輸和存儲過程中必須處于折疊狀態。

(3)所有集裝箱的箱型均為40 ft。

(4)空箱只能存于城市節點的集裝箱場站，不能存于貨源客戶節點。

(5)采用海陸聯運方式的空箱調運的路徑已知。

(6)在每個時期內，貨源客戶的空箱需求必須被滿足。

2.2 符號說明

參數、集合、決策變量以及數學符號見表1。

2.3 數學模型

在構建模型時，主要考慮各節點的流量平衡約束。各節點流量平衡主要以空箱庫存量平衡為主，取決于前后兩時期內流入與流出節點的空箱量。空箱進出示意見圖2，其中縱軸代表不同節點，橫軸代表決策周期。由圖2(a)、圖2(b)可知，流入城市節點的空箱量包括上一時期末的空箱庫存量、從其他城市節點調運空箱量、該時期內的空箱供給量以及租箱量，流出城市節點的空箱量包括該時期末的空箱庫存量以及調運到其他城市節點及客戶節點的空箱量。由圖2(c)可知，客戶節點空箱流入量即為班列公司調往客戶節點的標準集裝箱空箱量與可折疊集裝箱空箱量，流出量為客戶節點的空箱需求量。

由于任意客戶節點m的空箱需求量具有不確定性，為了滿足該類節點的空箱需求，至少以概率ε使得客戶節點m在任意周期t可用集裝箱的數量ζmt不小于需求量，即P(ζmt≥dmt)≥ε。進一步，第t周期節點m可用集裝箱的數量ζmt取決于空箱調入量，即

?m∈Mt∈T

(1)

重新表達概率式為

(2)

分布式魯棒機會約束中歐班列空箱調運優化模型為

(3)

(4)

(5)

(6)

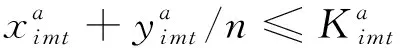
?i∈Nm∈Mt∈Ta∈A

(7)

(8)

?i∈Nt∈T

(9)

?i∈Nt∈T

(10)

?m∈Mt∈T

(11)

表1 相關符號說明

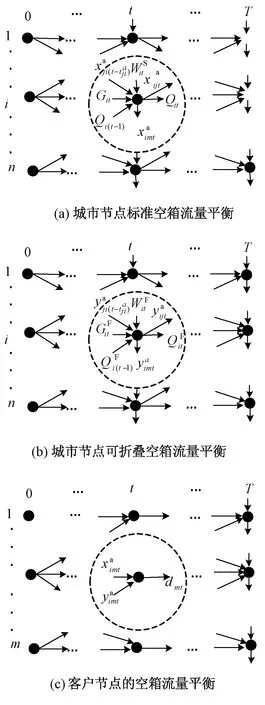
圖2 空箱進出流量示意圖

目標函式(3)為最小化所有成本總和，各項成本分別為調運成本、租箱成本、存儲成本以及可折疊集裝箱的折疊與展開成本。式(4)、式(5)分別表示城市節點場站的標準集裝箱、可折疊集裝箱的空箱庫存量平衡約束。式(6)、式(7)表示節點間運輸容量限制。式(8)表示城市節點場站的空箱堆存容量限制。式(9)、式(10)分別表示可折疊空箱折疊數量約束、展開數量約束。式(11)表示不確定空箱需求節點的空箱需求量最壞分布情況下的機會約束。

將該機會約束轉化為確定性約束

?m∈Mt∈T

(12)

為了完成證明過程，給出引理1：機會約束式(11)等價于

(13)

證明：對于?m∈M,t∈T，定義函數

(14)

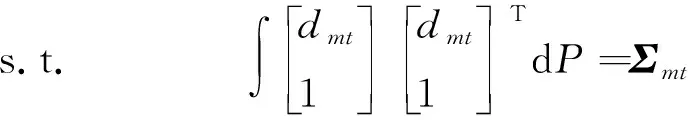
(15)

引入拉格朗日乘積項變量矩陣Mmt，將上述帶有約束的優化模型問題轉化為無約束極值問題的求解：

(16)

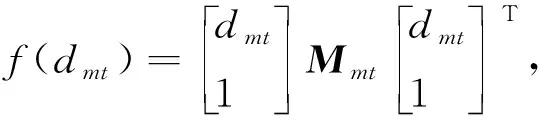
(17)

其中：

當且僅當θ(dmt)-f(dmt)≤0，式(17)有極小值，此時存在以下兩種情形：

(1)f(dmt)≥0,?dmt∈R。

(2)f(dmt)≥1，?dmt∈R,滿足ζmt≤dmt。

情形(1)等價于Mmt?0，情形(2)成立當且僅當存在λmt≥0使得：f(dmt)≥1-2λmt(ζmt-dmt)。

通過情形(1)、(2)可以得到存在λmt≥0，使得

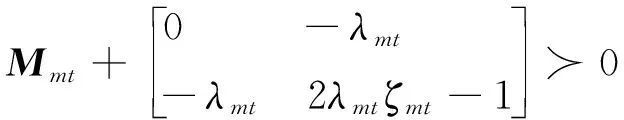
(18)

所以，優化問題式(15)等價于

min〈Mmt,Σmt〉

s.t.λmt≥0Mmt?0

(19)

進一步，機會約束式(11)等價于式(13)。

在文獻[15]中，給出如下兩條性質等價：

式中：0<ω≤1;Γ為協方差矩陣；x為期望向量；w為分配向量；γ∈R。

(2)存在一個對稱矩陣M和τ∈R+，使得

(20)

將式(13)各式兩邊除以λmt，并再次用將λmt替換1/λmt，用Mmt替換Mmt/λmt，得到

(21)

因此根據式(20)，可將機會約束問題最終轉換為

?m∈Mt∈T

3 數值實驗與靈敏度分析

3.1 算例背景

“一帶一路”戰略提出以來，各城市紛紛開通中歐班列。文獻[1]指出在2016年連歐、蘇滿歐、義新歐、漢歐、蓉歐、渝新歐、鄭歐以及營滿歐8條線路的貨流量達131 500 TEU，占據中歐班列貨運總量的78.5%。結合貨流量情況，本文選取全國主要城市的班列開通情況進行空箱調運優化的研究，見表2。

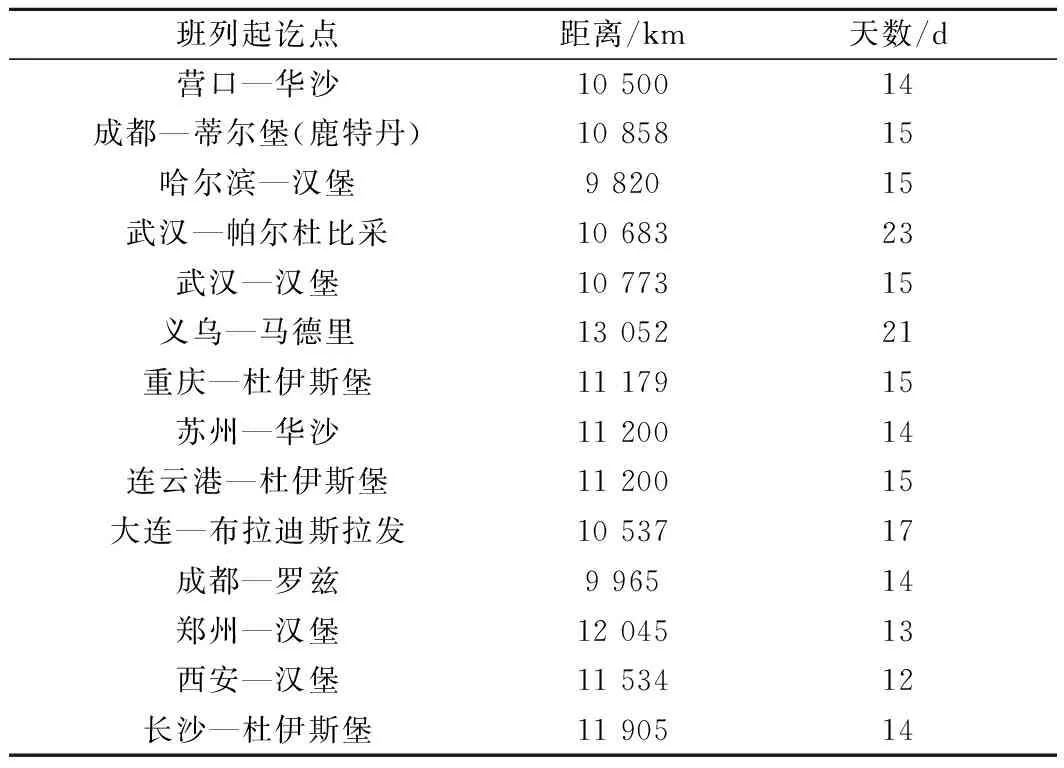
表2 主要城市班列開通情況

設置每個計劃周期長度為25 d，計劃周期數為12。考慮到海上運輸時間較長，空箱若通過海陸聯運方式調運，則需要在下一周期變為可用狀態。在本算例中，將各城市確定性客戶和不確定客戶分別簡化為一個整體，每個周期內確定性客戶的空箱需求量、不確定客戶的空箱需求均值、方差以及各城市空箱供給量隨機產生。假定各城市節點初始空箱量為0，最大庫存量不超過1 500 TEU。在同一區域內，各城市間標準空箱通過公、鐵、海3種運輸方式的單位運輸成本分別為1.6、0.8、0.4元/km。當標準空箱在跨區域間運輸時，通過班列運輸的單位運輸成本為0.5元/km。標準空箱的單位租箱成本6 000元/周期。標準空箱的單位存儲成本為600元/周期。可折疊集裝箱折疊成一個標準集裝箱空間所需要的數量為4，因此可折疊集裝箱各運輸方式單位運輸成本、單位存儲成本為標準集裝箱的四分之一。可折疊集裝箱單位租箱成本為12 000元/TEU，折疊和展開成本均為30元/TEU。機會約束的概率下界值為0.9。

3.2 實驗結果

本文采用CPLEX 12.6.2對所有模型進行求解，運用Windows7操作系統的i5-6440 CPU處理器進行運算。

3.2.1 結果分析

算例計算結果見表3。其中，數字1代表標準集裝箱，數字2代表可折疊集裝箱。在12個計劃周期內，由于陸上的單位運輸成本高于海陸聯運的單位運輸成本，當不考慮海陸聯運方式時，總運輸成本增加了3 655.85萬元，這使得考慮海陸聯運方式的空箱調運總成本減少了3 404.98萬元。與此同時，在本算例中標準空箱的單位運輸成本和單位存儲成本之和不大于單位租箱成本，這勢必會較少租箱，并使得存儲成本降為0元。最終結果表明，一部分空箱通過海陸聯運方式調回，能夠極大地降低總成本。

表3 計算結果 萬元

3.2.1 靈敏度分析

分析需求量變化、標準空箱與可折疊空箱供給比例變化、機會約束的概率下界值變化、不確定需求方差變化、相關單位成本變化對中歐班列空箱調運成本的影響。

(1)空箱需求量變化分析

空箱需求量增減情況下各項成本的變化情況見表4。空箱調運總成本隨著需求量的增加而變大。在本算例中，當空箱需求量增加時，出現了需求大于供給的情形，會進行額外的租箱，使得租箱成本持續增加。此時由于單位運輸成本和單位存儲成本之和不大于單位租箱成本，存儲成本會變為0。當空箱需求量減少時，會減少租箱，使得租箱成本驟減。當減少至原有值的10%以上時，出現了需求遠小于供給的情形，此時租箱成本會逐漸變為0。當需求量由5%增至20%時，運輸成本反而減少。當需求量減小5%時，運輸成本反而增加。兩次轉折的主要原因是通過優化可折疊集裝箱的調運量，能夠實現總成本的降低。當需求量由5%減少至20%時，空箱調運的總成本在減少后又開始增加，這主要是存儲成本上升導致的。

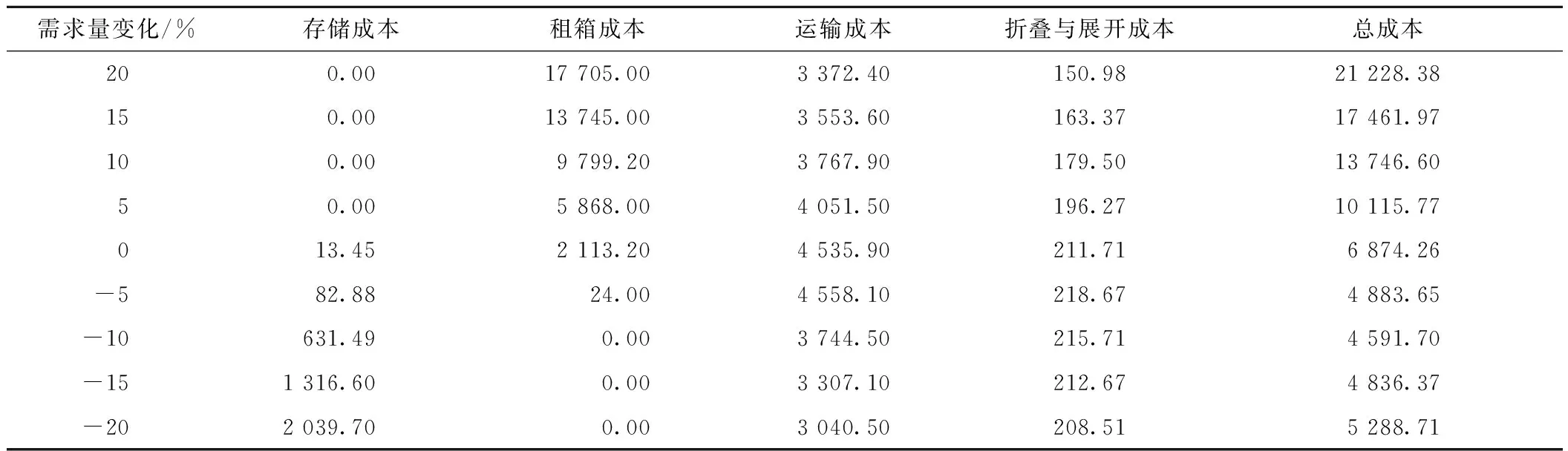
表4 需求量增減下的各項成本變化 萬元

(2)標準空箱與可折疊空箱供給比例變化分析

通過調節標準空箱與可折疊空箱供給比例的變化，探究使用可折疊集裝箱降低空箱調運總成本的潛在可能性。由表5可知，當可折疊集裝箱供給量為0時，空箱調運的總成本最高。隨著可折疊集裝箱供給量比例的增加，空箱調運各項成本也在發生變化。當供給比例由0增至20%時，總成本減少4 726.99萬元，當供給比例增長至50%以上時，總成本減少的程度大大降低。可見，在實際情形中，需合理地調整兩者的比例，才能更好地降低總成本。

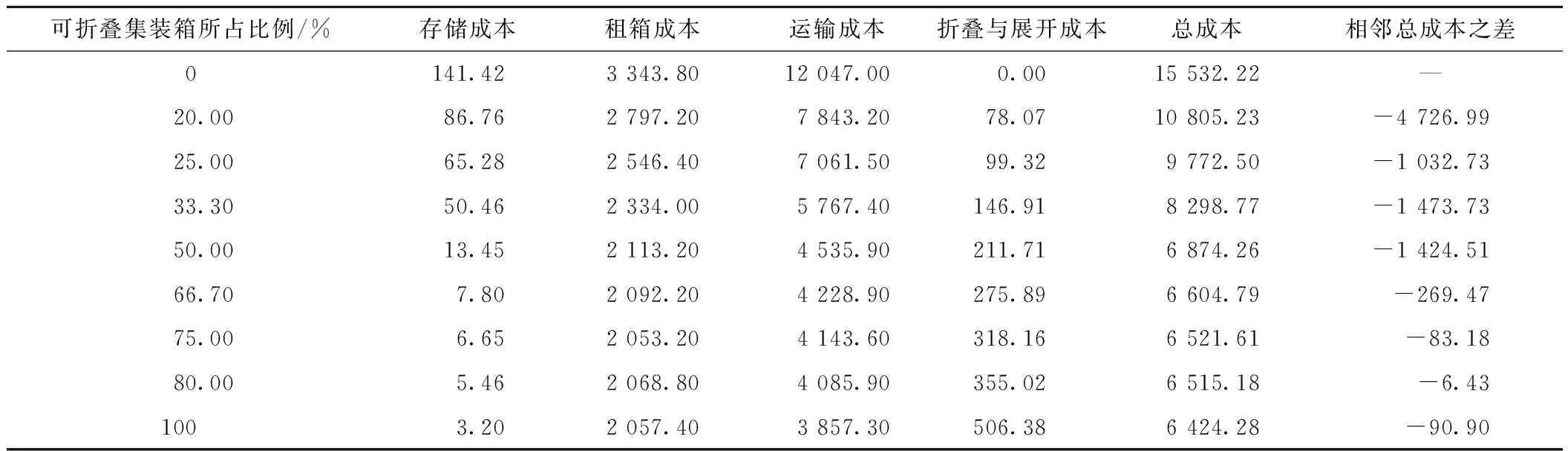
表5 可折疊集裝箱不同供給比例下的各項成本變化 萬元

(3)機會約束的概率下界值、不確定需求方差變化分析

由式(12)可知，機會約束的概率下界值與不確定需求方差發生變化時，會導致用來滿足不確定需求客戶的空箱量發生變化。表6、表7分別給出了兩者變化后各項成本的變化情況。當兩者增大時，會導致式(12)左邊數值的增加，從而需要增加空箱的調運量，這使得總成本在逐漸增加，并且會使存儲成本降為0。這也驗證了本文的分布式魯棒機會約束優化是以最壞情況下的優化為基礎，從而得到具有魯棒性的優化方案。

(4)單位租箱成本變化分析

單位租箱成本是影響空箱調運優化的關鍵參數，單位租箱成本變化后各項成本的變化情況見表8。可以看出，空箱調運總成本會隨著單位租箱成本的增加逐漸變大。當單位租箱成本增加30%以上時，存儲成本、運輸成本、折疊展開成本保持不變，但租箱成本發生變化。此時，單位租箱成本已遠遠超過單位運輸成本與單位存儲成本之和，導致租箱量減少。但由于需求大于供給，系統還會向外界租箱，因此租箱成本增加。當單位租箱成本減少時，會增加租箱量，同時也會導致存儲量增加，調運量減少。因此，存儲成本會隨著租箱量的增加而增加，相反運輸成本會隨著租箱量的減少而減少。

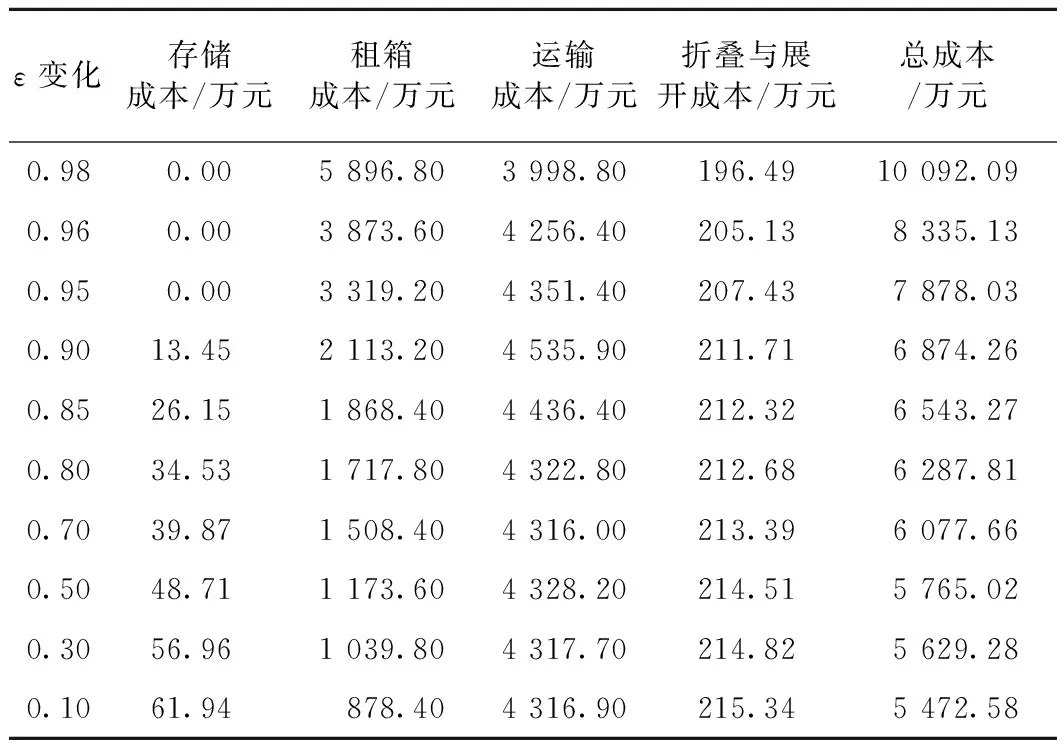
表6 不同機會約束的概率下界值下的各項成本變化

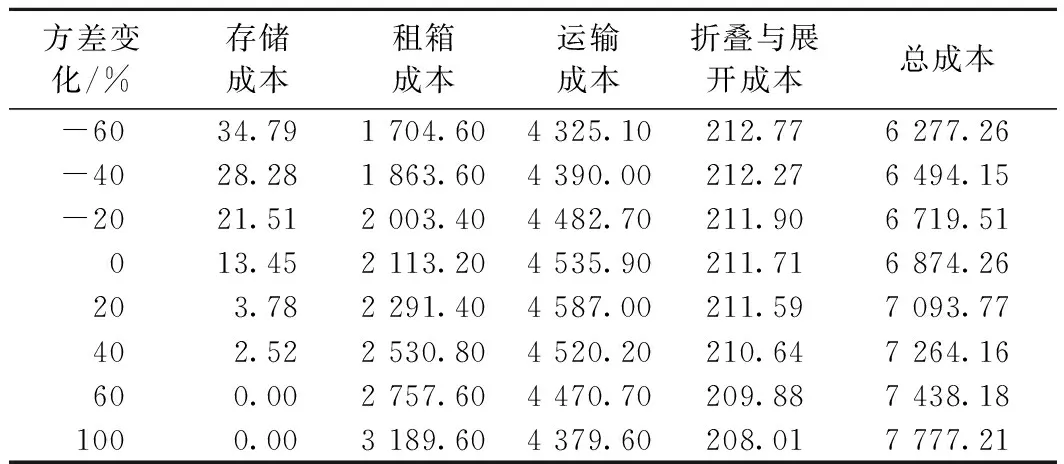
表7 方差變化下的各項成本變化 萬元

表8 單位租箱成本變化下的各項成本變化 萬元

(5)單位運輸成本變化分析

單位運輸成本變化后各項成本的變化情況見表9。可以看出，空箱調運總成本會隨著單位運輸成本的增加逐漸變大。當單位運輸成本減少30%以上時，存儲成本、租箱成本、折疊展開成本保持不變，但運輸成本減少。由于需求大于供給，系統還會向外界租箱，但租箱量不變，因此租箱成本不變。存儲成本不變、折疊展開成本不變、運輸成本減少都是此時的系統以調箱為主，且調箱量不變導致的。綜合表8、表9可知，在供給不小于需求的情況下，若單位租箱成本低于單位運輸成本，則優化結果偏向于租箱；若單位租箱成本高于單位運輸成本，則優化結果偏向于調運。

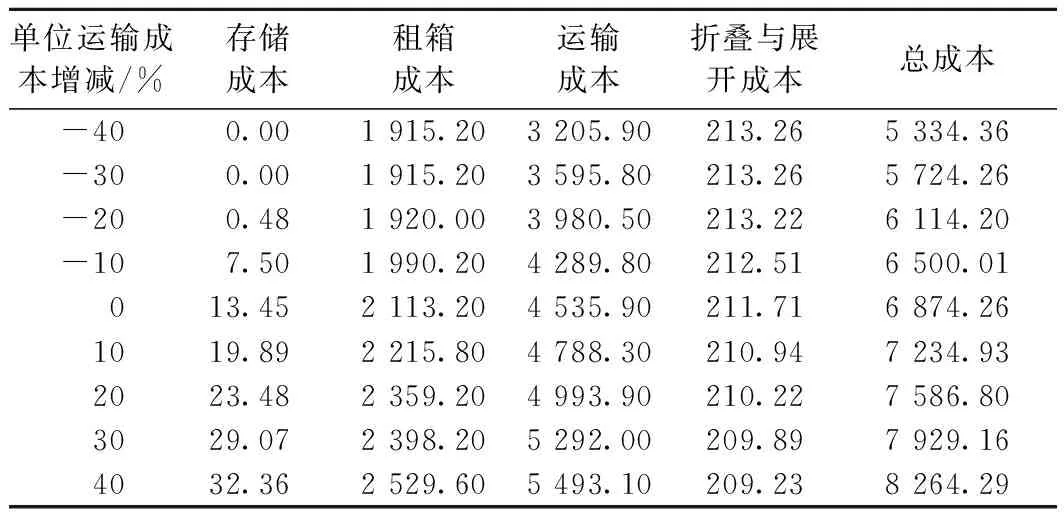
表9 單位運輸成本變化下的各項成本變化 萬元

(6)不同供需比例下的參數變化情形分析

圖3給出了供給接近于需求、供給遠小于需求、供給遠大于需求3種情形下的單位運輸成本與可折疊集裝箱所占供給比例兩種參數變化對成本的影響。可以看出3種供需關系下的總成本都會隨著可折疊集裝箱供給比例的增加而減少、隨著單位運輸成本的增加而增大。在3種情形下，當可折疊集裝箱供給比例由0增至20%時，空箱調運總成本急劇降低，大約降低了一半。當可折疊集裝箱供給比例由20%增至50%時，空箱調運總成本降低的趨勢有所減緩。當可折疊集裝箱供給比例達到75%以上時，空箱調運總成本的降低不顯著。考慮到可折疊集裝箱的獲得成本相對較高，在需求量較大的情況下，應適當減少可折疊集裝箱的投入比例。此外，在3種供需關系下，隨著運輸成本的增加，使用可折疊集裝箱將能極大減少總成本。

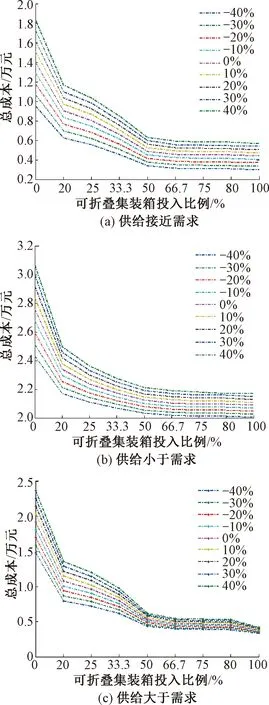
圖3 三種供需關系下的兩種參數變化對總成本的影響

4 結論

本文評估了考慮海陸聯運方式、使用可折疊集裝箱為不確定環境下的中歐班列空箱調運減少成本的可行性，并分析了不同參數變化對總成本的影響。結果表明：第一，部分空箱通過海陸聯運調回能夠極大地降低總成本。第二，機會約束的概率下界值或不確定需求方差增大時，會導致式(12)左邊數值的增加，從而需要增加空箱的調運量，這使得總成本在逐漸增加。第三，在可折疊集裝箱供給方面，空箱調運各項成本會隨著可折疊集裝箱供給比例變化而改變。在三種需求情形下，班列公司只需適當投入適量的可折疊集裝箱就能極大地降低總成本。因此，在實際情形中，合理調整標準、可折疊集裝箱的投入比例會更好地降低空箱調運總成本。第四，單位運輸成本及單位租箱成本是影響空箱調運優化的關鍵參數，且兩者具有很大的相關性。進一步的研究將集中在重箱與空箱運輸的協同優化問題。