基于點線一體化的高速鐵路通過能力計算研究

王宇強，方 波，魏玉光，韓學雷

(北京交通大學 交通運輸學院，北京 100044)

近年來我國高速鐵路(以下簡稱高鐵)發展迅速，對準確掌握和評估高鐵通過能力提出了更高要求，高鐵通過能力計算及相關理論研究已成為鐵路運輸組織領域的熱點。與其他國家相比，我國高鐵運輸組織模式復雜多樣且自成體系，然而已有的通過能力計算方法或借鑒既有線[1]，或直接采用國外算法，方法復雜且針對性不強。本文將車站虛擬為區間，提出了車站區間一體化的高鐵通過能力計算新方法。

1 研究高鐵通過能力的新思路

1.1 現有計算方法

高鐵通過能力是指在一定的高鐵基礎設施運用標準、列車運行技術裝備運用指標和旅客列車開行方案條件下，一個客流區段在列車運行圖有效時間內可放行的最大列車數或列車對數，一般按區段或方向確定。需分別計算區間通過能力和車站通過能力后，取其中較小值作為高鐵通過能力。

高鐵區間通過能力計算方法主要包括扣除系數法、平均最小列車間隔法、日本的山岸式計算法和計算機模擬法4種[2]。文獻[3]研究了扣除系數法在高鐵中的應用，分析了不同等級列車越行區段選取方法和列車的共用停站分組方法，在此基礎上提出了基于低等級列車扣除系數與列車停站扣除系數的高鐵能力計算方法。但扣除系數法由普速列車發展而來，并不適用于高鐵高質量的運輸組織模式，且對于扣除系數的選擇需要很高的精確度，增加了計算難度。對于平均最小列車間隔法，文獻[4]在高鐵無越行區段上，根據對其標準通過能力和使用通過能力及使用通過能力彈性系數的定義，提出基于列車運行圖平均最小列車間隔時間的區段標準通過能力和考慮列車運行圖緩沖時間的區段使用通過能力的計算方法；文獻[5-6]系統介紹了平均最小列車間隔法。對于日本山岸式，文獻[7]給出了其計算方法及適用環境。但平均最小列車間隔法和日本山岸式只考慮了本線列車，顯然不適用于我國復雜的網狀運輸模式。對于計算機模擬法，文獻[8-10]分析了高鐵通過能力的影響因素，提出了新的通過能力計算模型，通過計算機編程求解模型，最后結合實際客流區段對方法進行了驗證。但計算機模擬法的計算結果中可行解較多，最優方案比選困難。

在高鐵車站通過能力計算方面，主要采用分析計算法、圖解法和計算機模擬仿真法，其中計算機模擬仿真法的本質就是圖解法。對于分析計算法，文獻[11]給出了客運站到發能力、咽喉通過能力、客車整備場通過能力的利用率計算公式和方法。但其公式中參數查定的方法較為復雜。對于圖解法，由于其工作量大且難度大已被計算機模擬法取代。對于計算機模擬仿真法，文獻[12]提出不同層次車站理論通過能力的計算方法，利用壓縮加密模型和自行開發的仿真系統進行案例驗證；文獻[13]運用計算機仿真的方法，將到發線和咽喉區的作業相互協調配合，計算出一天繁忙時段車站所能接發列車的總和，即車站高峰小時通過能力。雖然計算機模擬仿真法計算精度高，但隨著車站規模的增大解空間會相應增大，對系統的求解效率有很高的要求。

1.2 基于點線一體化的高鐵通過能力計算思路

可以看出，現有計算方法都沒有把車站和區間的通過能力統籌考慮，導致計算過程復雜，可實施性差。高鐵動車組列車在車站作業簡單，主要為列車始發、終到、通過、待避停站、為完成旅客乘降作業的停站和一些跨線列車作業，均與區間運行過程直接相關，如把列車在車站的作業過程簡化后用運行線表示，那么車站就可以虛擬為一個有長度的區間，則高鐵“車站-區間-車站…”的布局模式就變成“虛擬區間-區間-虛擬區間…”的連續多個區間分布形式，按照通過能力理論，分析得到可能成為高鐵能力限制的區間，分別計算這些區間的通過能力后，通過比較取其中最小者為限制區間通過能力即該區段的通過能力。由于高速列車在車站的開行模式決定了列車在區間的開行模式，因此高鐵能力一般受限于車站而不是區間，也就是車站的通過能力決定著整個區段的通過能力。因此，計算高鐵通過能力就轉化為求各車站即虛擬區間的通過能力，采用平均最小列車間隔時間法計算虛擬區間通過能力，并確定限制區間，即為該區段的通過能力。基于點線一體化的高鐵通過能力計算方法的步驟為：

(1)車站虛擬化。將車站轉化為虛擬區間后，分析不同列車在虛擬區間的運行線，有越行關系的列車要進一步虛擬運行線。

(2)最小列車間隔時間計算。把兩兩相鄰的追蹤列車作為虛擬區間運行圖的基本結構單元，分析不同列車組合在虛擬區間的最小列車間隔時間。

(3)虛擬區間通過能力計算。在現有列車開行方案條件下，分析高速列車數量和種類，求平均最小列車間隔時間，計算有效作業時間內可放行的列車對數。

(4)確定限制區間。將該區段各個大型客運站虛擬化為區間后分析計算得到通過能力最小的車站，為該區段的通過能力。

2 基于點線一體化的高鐵通過能力計算方法

2.1 虛擬區間的定義

為方便處理列車停站、越行以及其他作業和跨線列車對高鐵通過能力計算的影響，簡化運行圖結構，將車站虛擬為一個有長度的區間，那么列車各項作業就會轉換成列車在此區間內不間斷運行的過程，從而將復雜的車站通過能力求解轉化為簡單的區間通過能力求解，簡化求解過程，提高求解精度。本文將此區間定義為虛擬區間。

虛擬區間建立過程見圖1。線路上有A、B、C 3個車站，假設列車1、2、3、4為相同速度類型的列車，其中列車1、2、3在B站有停車作業，列車4直接通過B站，且列車4會在B站越行列車3，如圖1(a)所示。以原B站為中心線，可以將有列車停車作業的B站虛擬為一個虛擬閉塞分區BB′，如圖1(b)所示。此時列車1′、2′、3′變成不停站直接通過BB′區間，但是通過該虛擬區間的虛擬速度也將降低；而列車4′本來就是直接通過B站，故構建虛擬區間后，列車在此區間的運行時間為0，在運行圖上表現為一段豎直線。

圖1 虛擬區間的構建

為簡化有越行情況的計算過程，提出虛擬運行線的概念，虛擬運行線的構建過程見圖2。圖2(a)為列車1、2在虛擬區間BB′應有的運行線，通過將列車1在虛擬區間BB′的運行線直接連接到列車2在B′C區間的運行線上，列車2在虛擬區間BB′的運行線直接連接到列車1在B′C區間的運行線上，就可以構建出兩條新的虛擬運行線，即1′和2′，如圖2(b)所示，此方法可在虛擬區間中將待避列車和越行列車視為兩列前后追蹤的停站列車。

所有類型列車在實際車站與虛擬區間的運行線見圖3。

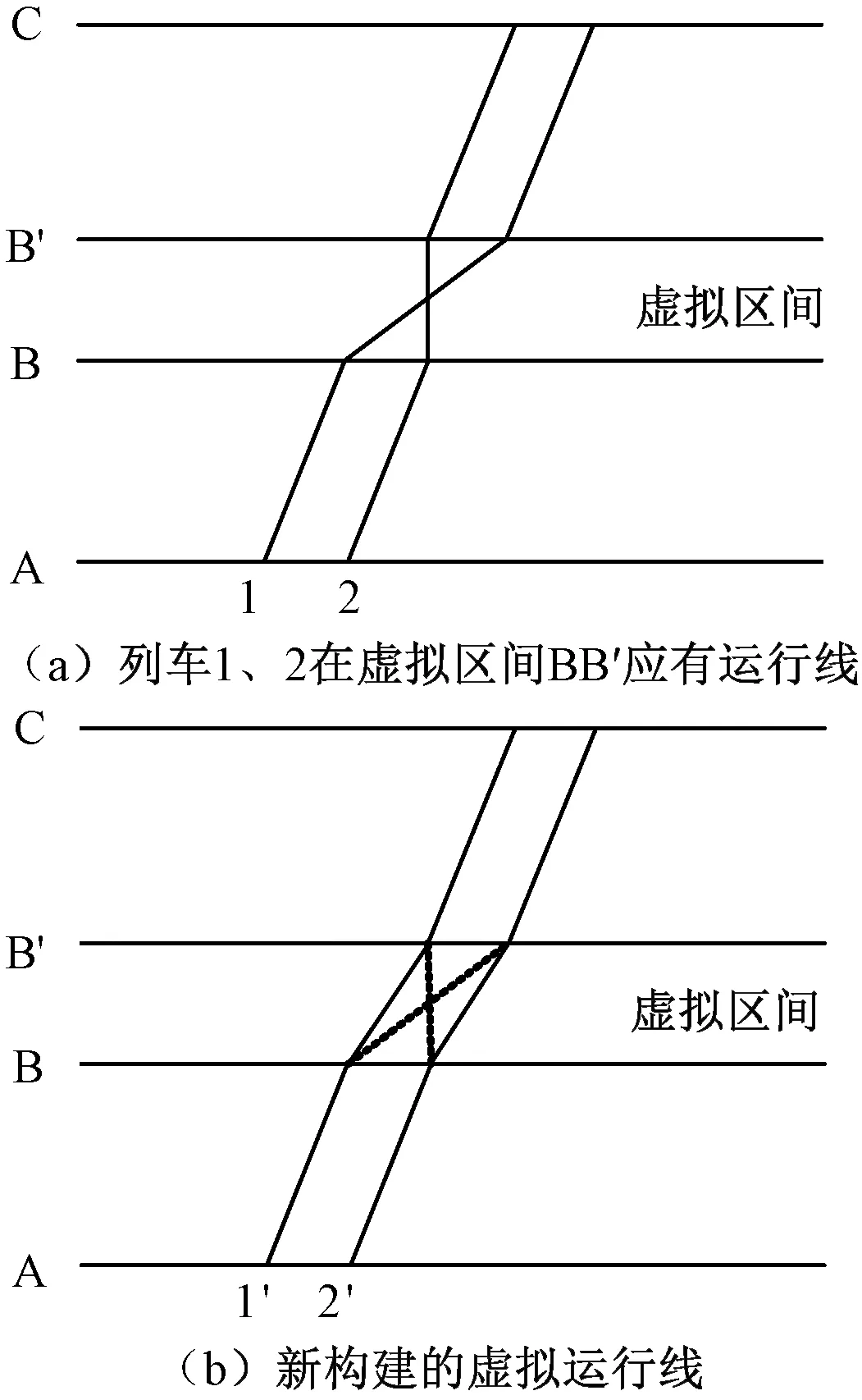
圖2 有越行情況時虛擬運行線的構建

圖3 車站虛擬化運行線

2.2 運行列車組分組及其間隔時間

若將兩兩相鄰的追蹤列車定義為運行列車組，則可視列車運行圖由若干運行列車組的運行線組成。將虛擬區間兩兩相鄰的列車也視為運行列車組，即可分析得到不同列車的組合及其在虛擬區間的最小列車間隔時間。

(1)“發到”和“到發”運行列車組

當第一列車為始發列車、第二列車為終到列車時，由虛擬區間運行線可得最小列車間隔時間為I發到，見圖4。

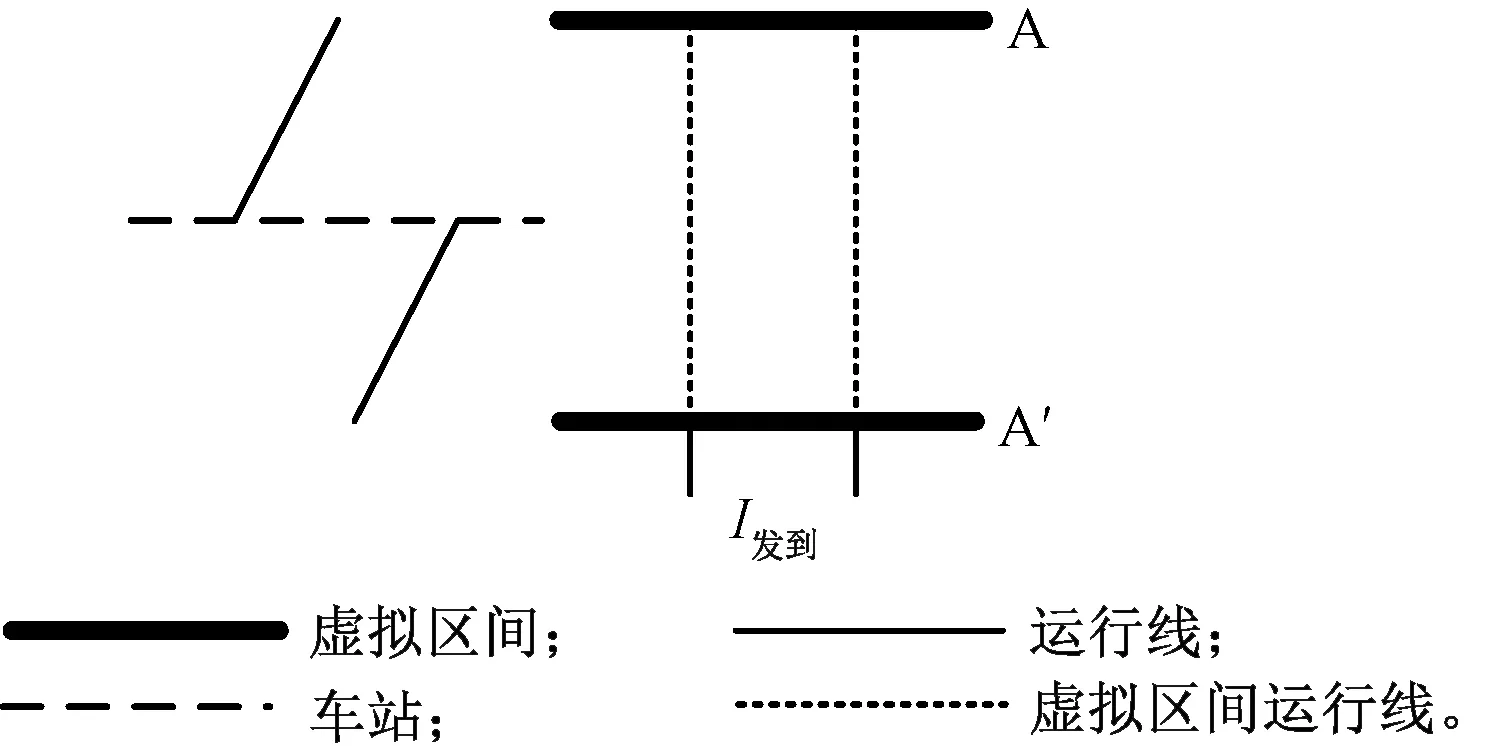
圖4 “到發”運行列車組示意圖

同理，當第一列車為終到列車、第二列車為始發列車時，虛擬區間運行線仍和圖4類似，但最小列車間隔時間為I到發。

(2)“發通”和“通發”運行列車組

當第一列車為始發列車、第二列車為通過列車時，由虛擬區間運行線可得兩列車最小列車間隔時間為I發通， 見圖5。

圖5 “發通”運行列車組示意圖

同理，當第一列車為通過列車、第二列車為始發列車時，虛擬區間運行線仍和圖5類似，但最小列車間隔時間為I通發。

(3)“發發”運行列車組

當兩相鄰列車在車站都是始發列車時，由虛擬區間運行線可得最小列車間隔時間為I發，見圖6。

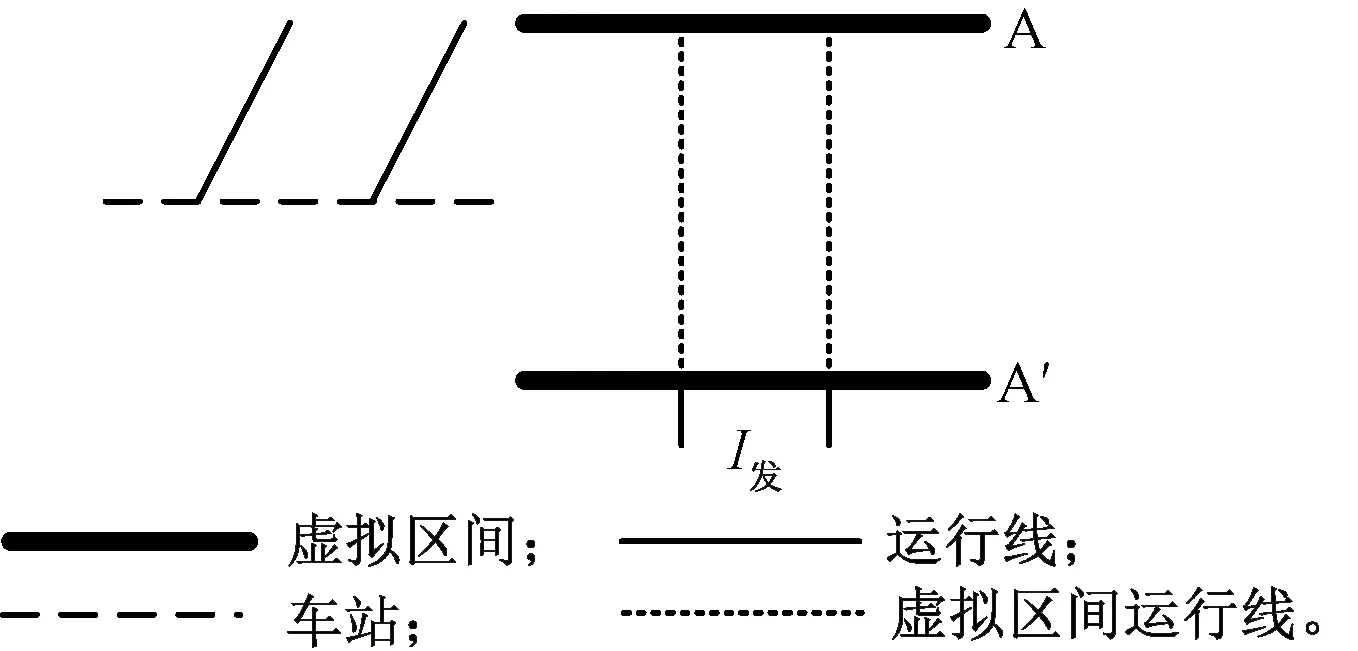
圖6 “發發”運行列車組示意圖

(4)“發停”和“停發”運行列車組

當第一列車為始發列車、第二列車為停站列車時，由虛擬區間運行線可得最小列車間隔時間為I發到，見圖7(a)。同理，當第一列車為停站列車、第二列車為始發列車時，兩列車虛擬區間運行線位置見圖7(b)，此時的最小列車間隔時間為I發+t停,t停為停站時間，min。

圖7 “發停”與“停發”運行列車組示意圖

(5)“通到”和“到通”運行列車組

當第一列車為通過列車、第二列車為終到列車時，由虛擬區間運行線可得最小列車間隔時間為I通到，見圖8。

圖8 “通到”運行列車組示意圖

同理，當第一列車為終到列車、第二列車為通過列車時，虛擬區間運行線仍和圖7類似，最小列車間隔時間為I到通。

(6)“到停”和“停到”運行列車組

當第一列車為終到列車、第二列車為停站列車時，由虛擬區間運行線可得最小列車間隔時間為I到，見圖9。

圖9 “到停”運行列車組示意圖

同理，當第一列車為停站列車、第二列車為終到列車時，兩列車虛擬區間運行線位置和上圖順序相反，此時最小列車間隔時間為I發到+t停。

(7)“到到”運行列車組

當兩相鄰列車在車站都是終到列車時，由虛擬區間運行線可得最小列車間隔時間為I到，見圖10。

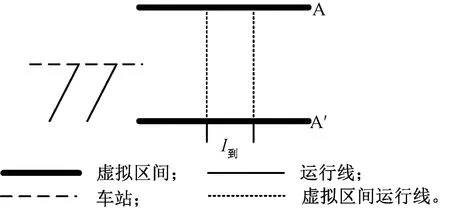
圖10 “到到”運行列車組示意圖

(8)“通通”運行列車組

當兩列車在車站都是通過時，由虛擬區間運行線可得最小列車間隔時間為I通，見圖11。

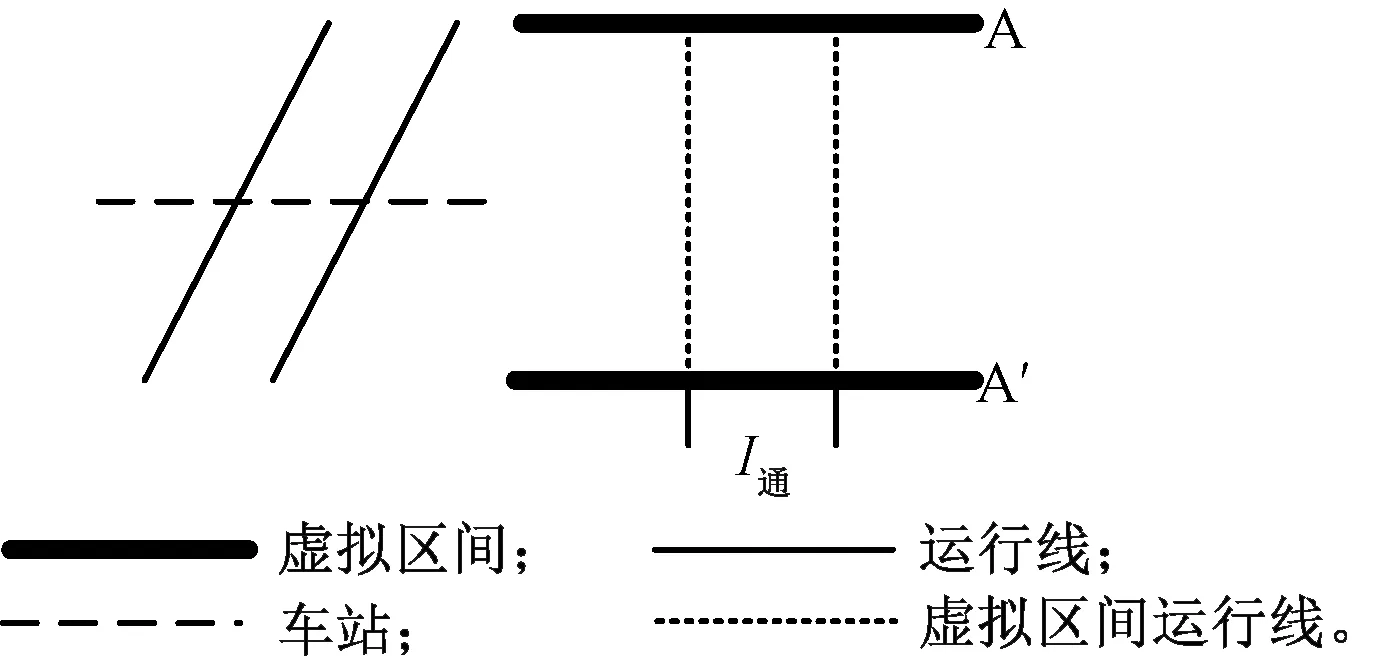
圖11 “通通”運行列車組示意圖

(9)“通停”和“停通”運行列車組

“通停”運行列車組是指前行列車為通過列車，后行列車為停站列車，由虛擬區間運行線可得最小列車間隔時間為I通到，見圖12。

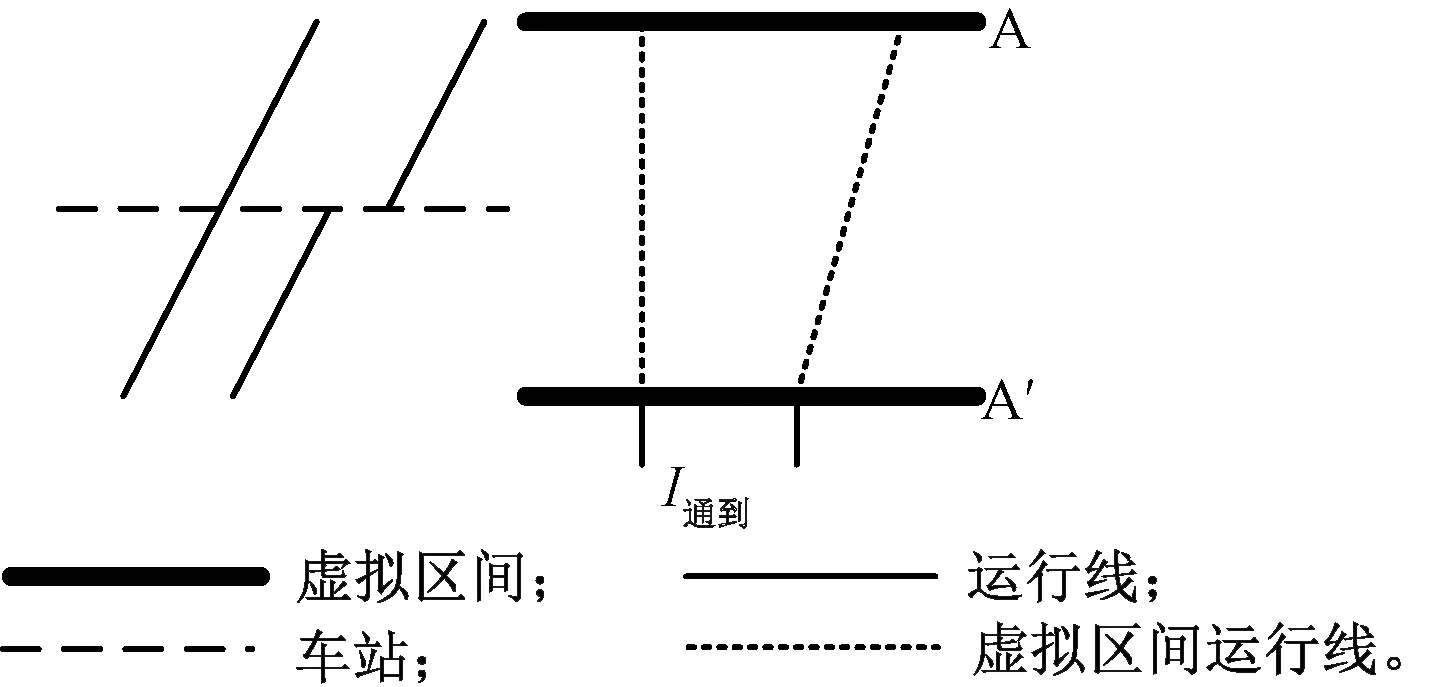
圖12 “通停”運行列車組示意圖

同理，當第一列車為停站列車、第二列車為通過列車時，虛擬區間運行線順序和上圖相反，此時的最小列車間隔時間為I發通+t停。

(10)“停停”運行列車組

“停停”運行列車組是指前后行列車為追蹤停站列車，由虛擬區間運行線可得最小列車間隔時間為I到，見圖13。

圖13 “停停”運行列車組示意圖

(11)待避越行列車組

越行列車和待避列車通過構造其虛擬運行線，可看作在虛擬區間中兩列追蹤的通過列車，方便后續的待避越行列車組的處理，見圖14。此時由虛擬運行線可得最小列車間隔時間為I到通。

圖14 待避越行列車組示意圖

(12)“通越”運行列車組

此處的“通越”運行列車組是指第一列車為通過列車，第二列車為待避越行列車組虛擬運行線的左半部分，也即待避越行列車組的第一條虛擬運行線，見圖15。此時由虛擬區間運行線可得最小列車間隔時間為I通到。

圖15 “通越”運行列車組示意圖

(13)“停越”運行列車組

此處的“停越”運行列車組是指第一列車為停站列車，第二列車為待避越行列車組虛擬運行線的左半部分，也即待避越行列車組的第一條虛擬運行線，見圖16。此時由虛擬區間運行線可得最小列車間隔時間為I發到+t停。

同理，當第一列車為“正接正發”的跨線列車時，與上述情況類似，但列車停站時間不一樣，最小列車間隔時間為I發到+t停。

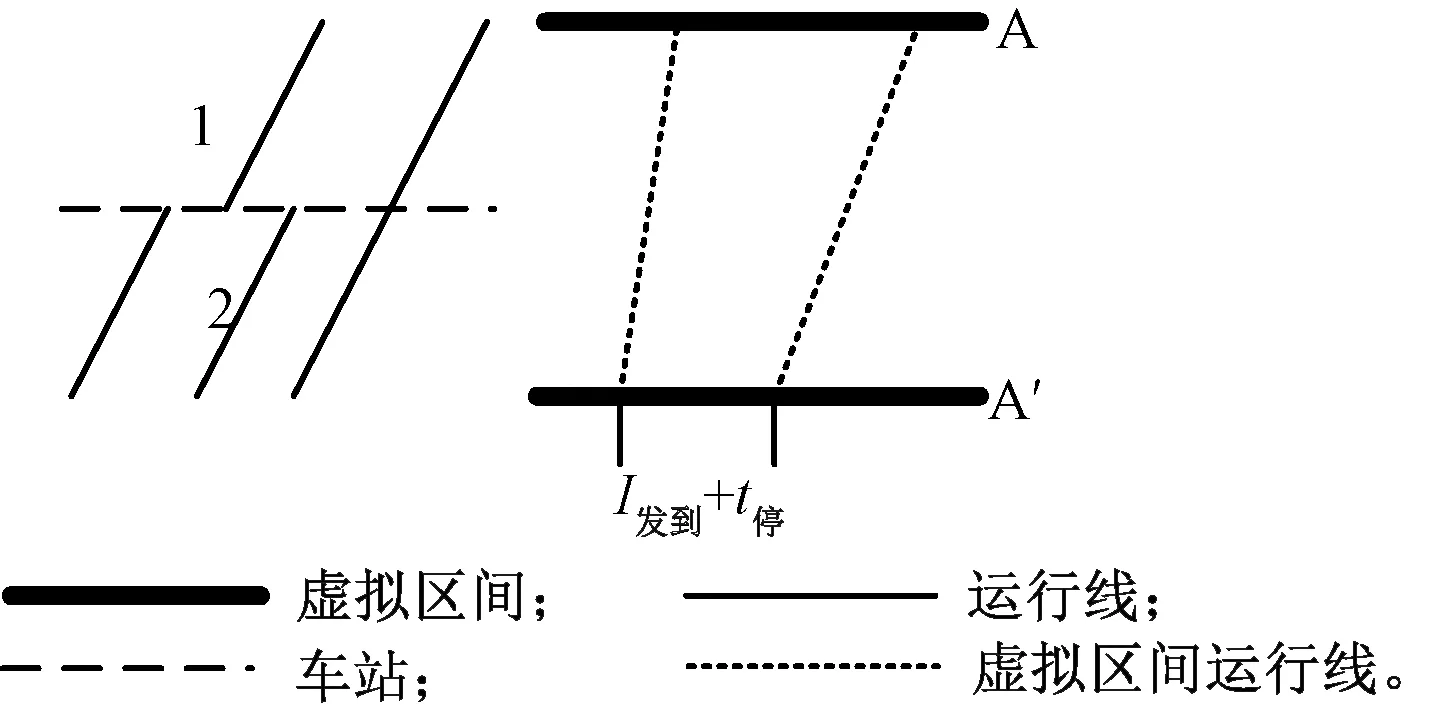
圖16 “停越”運行列車組示意圖

(14)“越通”運行列車組

此處的“越通”運行列車組是指第一列車為待避越行列車組虛擬運行線的右半部分，也即待避越行列車組的第二條虛擬運行線，第二列車為通過列車，見圖17。此時由虛擬區間運行線可得最小列車間隔時間為I通發+I發通。

圖17 “越通”運行列車組示意圖

(15)“越停”運行列車組

此處的“越停”運行列車組是指第一列車為待避越行列車組虛擬運行線的右半部分，也即待避越行列車組的第二條虛擬運行線，第二列車為停站列車，見圖18。此時虛擬區間運行線的最小列車間隔時間為I通發+I發到。

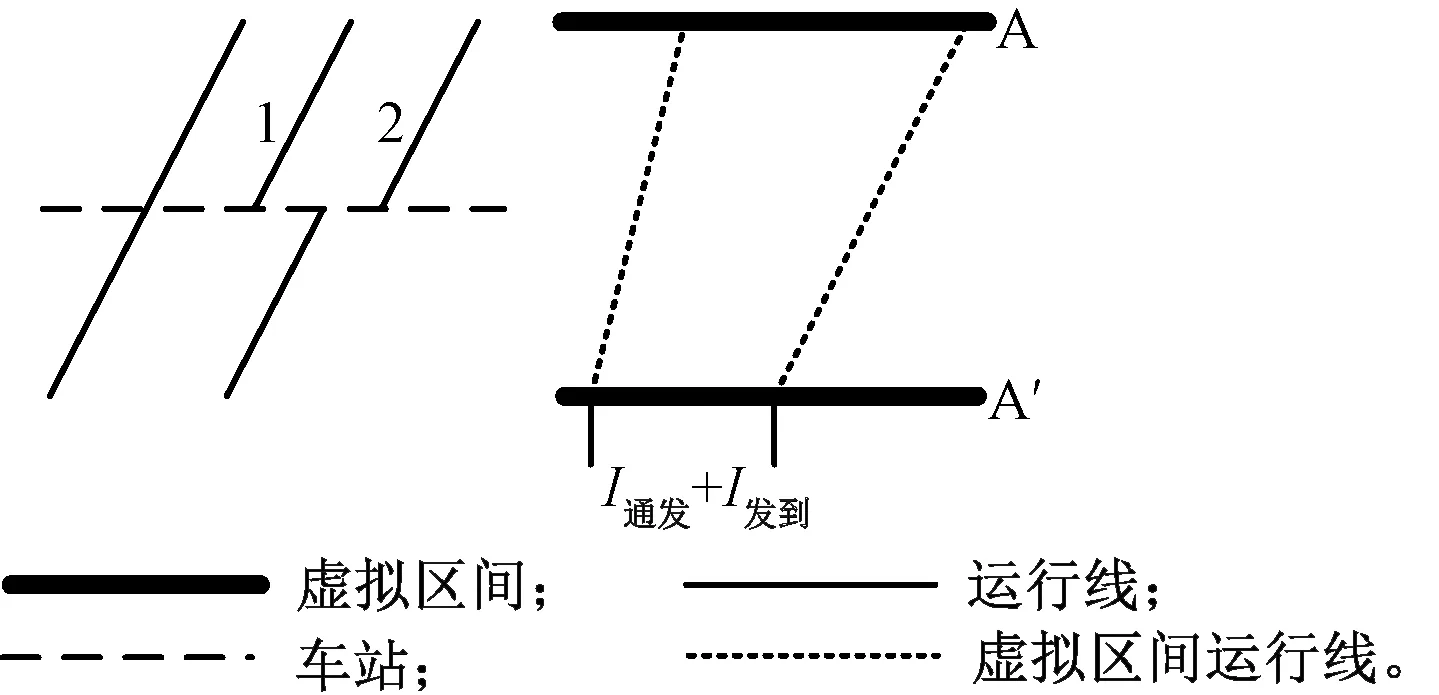
圖18 “越停”運行列車組示意圖

圖19 “反接正發”跨線列車和左半待避越行列車組示意圖

同理，當第二列車為“正接正發”的跨線列車時，與上述情況完全類似，最小列車間隔時間不變，仍為I通發+I發到。

(16)“反接正發”跨線列車和左半待避越行列車組

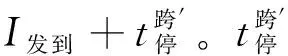
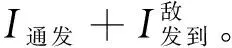
(17)“正接正發”跨線列車

跨線列車正向接入，正向發出，與普通的本線停站列車類似，但其停站時間與本線列車不同。有“正接正發”跨線列車時的運行列車組見圖20。

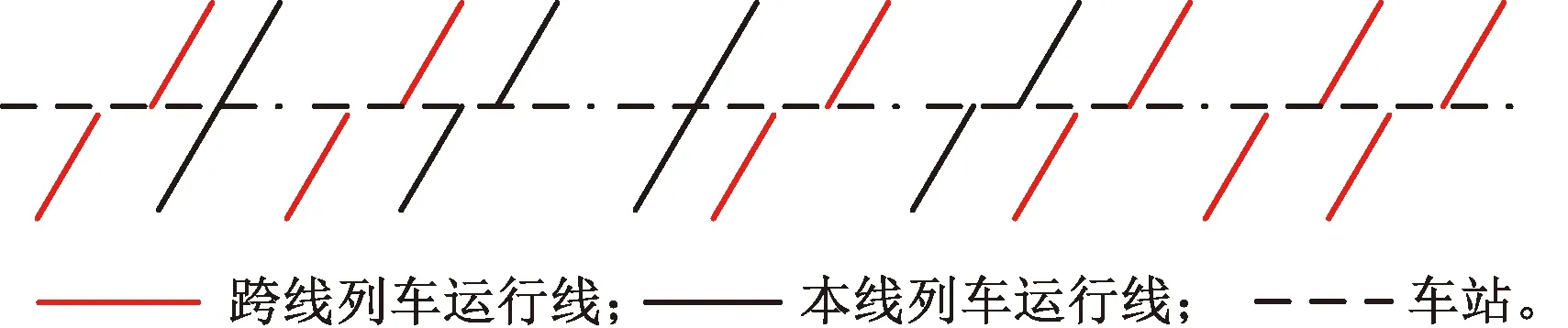
圖20 有“正接正發”跨線列車的列車組

根據上圖將車站虛擬區間化之后即可分別得到對應的虛擬區間運行線，見圖21。

圖21 有“正接正發”跨線列車的列車組虛擬區間運行線

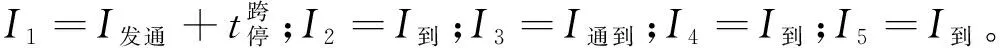
(18)“反接正發”跨線列車

跨線列車反向接入，正向發出，“反接正發”跨線列車的停站時間也與“正接正發”跨線列車的不同，需要注意區分。有“反接正發”跨線列車時的運行列車組見圖22。

圖22 有“反接正發”跨線列車的列車組

根據圖22將車站虛擬區間化之后既可分別得到上圖所對應的5種情況的虛擬區間運行線，見圖23。

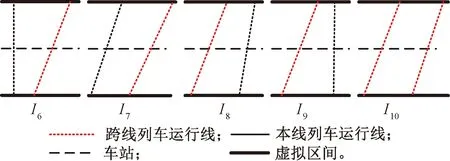
圖23 有“反接正發”跨線列車的列車組虛擬區間運行線

由圖23中列車運行線可知，相鄰跨線列車和本線列車的車間隔時間分別為

(19)相鄰“正接正發”和“反接正發”跨線列車

這種情況是指兩相鄰列車均為跨線列車，且一列為“正接正發”，另一列為“反接正發”。兩種跨線列車組合時的運行列車組見圖24。

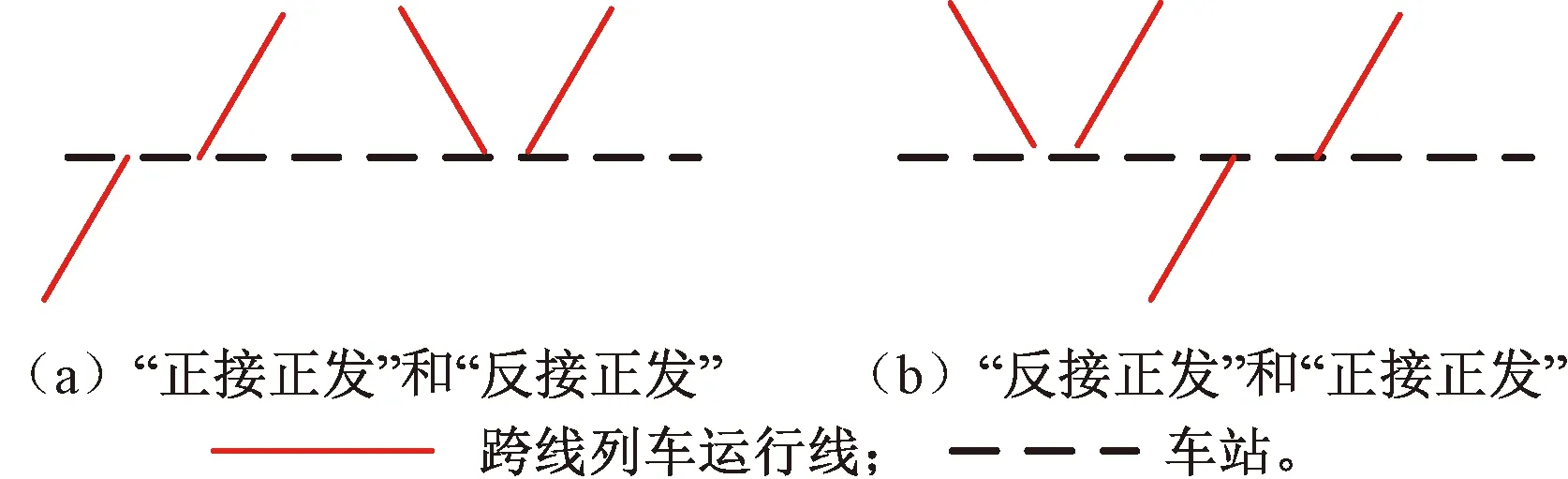
圖24 “反接正發”和“正接正發”跨線列車的列車組

根據圖24將車站虛擬區間化之后即可分別得到所對應的2種情況的虛擬區間運行線，見圖25。

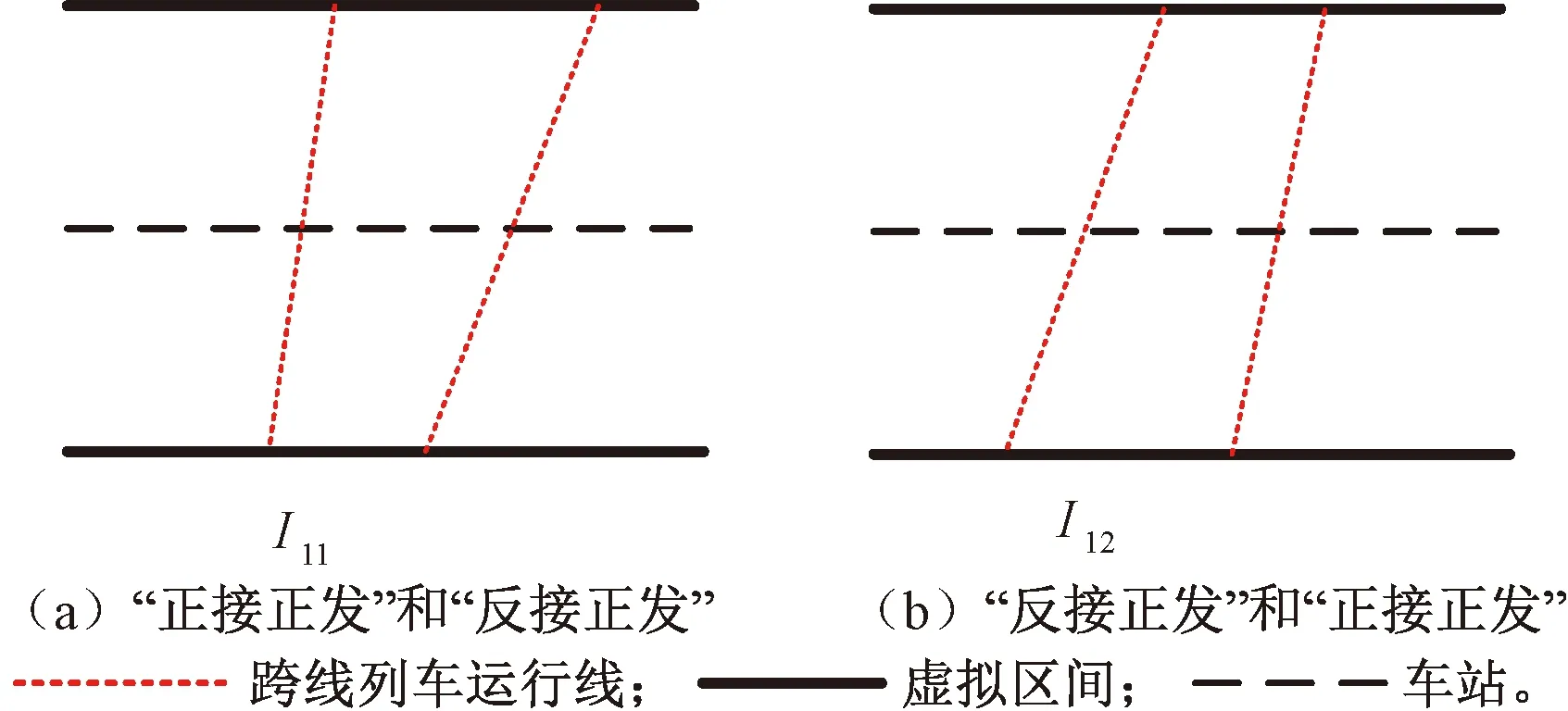
圖25 “反接正發”和“正接正發”跨線列車的列車組虛擬區間運行線

由圖25中列車運行線可知，跨線運行列車組的間隔時間分別為

因篇幅有限只考慮了以上幾種列車組類型，如果有需要的話其他類型列車組依然可根據此規律表示。

由此可知將車站虛擬為一個區間后，通過上述一一對應的關系確定了各列車組在虛擬區間的運行線與相應的列車間隔時間，在今后的運行圖鋪畫中可以直接使用該方法，在能力計算時可以直接使用新的列車間隔時間，也方便了對跨線列車的處理，使運行圖結構更加簡單、明了，能力的計算結果也更加符合實際情況。

2.3 虛擬區間通過能力計算

將車站虛擬為區間就可以使用最小列車間隔法來求解虛擬區間的通過能力，即車站的通過能力。N1為根據運行圖查定的某高鐵車站單方向一日接發的全部列車數，其中n1、n2、n3、n4和n5分別為本線列車中始發列車、終到列車、通過列車、僅停站列車和待避列車數；n6為跨線列車中“正接正發”列車數；n7為“反接正發”列車數。對于一些本線列車的“反接正發”和“正接反發”作業，該類情況一般出現在始發列車或終到列車中，情況較少，且與跨線列車造成的影響基本相同，所以將這些列車歸為跨線列車相應的類別中進行計算。

則在運行圖上出現上述某種列車的概率pi為

(1)

式中：i為列車種類組序號。

出現上述某種運行列車組的概率pij為

(2)

式中：i為運行列車組第一列車的列車種類組序號；j為運行列車組第二列車的列車種類組序號。

則運行列車組中某種列車組數nij為

(3)

不考慮其他因素，所有運行列車組在運行圖上占用虛擬區間的總時間B為

(4)

式中：Iij為i類列車與j類列車的最小列車間隔時間，min。

當考慮各方向跨線列車因切割車站咽喉而對研究方向列車占用虛擬區間總時間影響時，列車組在運行圖上占用虛擬區間的總時間B′為

(5)

式中：s為各方向跨線列車總類數，s≥1；xki表示k類跨線列車是否影響i類列車占用虛擬區間時間，xki=1為影響，xki=0為不影響；tki為k類跨線列車影響i類列車時增加的占用虛擬區間時間，min。

(6)

由于各個車站的運營時間不同，所以引入f為高鐵站一天的運營時間所占總時間的比例，那么虛擬區間通過能力，即車站通過能力N通為

(7)

式中：T為一天的時間，取1 440 min。

根據高鐵通過能力理論與本文提出的虛擬區間的概念，高鐵區段的能力限制區間為通過能力最小的虛擬區間，通過使用上述高鐵虛擬區間的能力計算方法，可以計算出該區段各大型客運站所對應的虛擬區間的通過能力，選其中最小者即為該區段的通過能力。

3 京滬高鐵通過能力計算

京滬高鐵是我國重要的高鐵通道，計算其能力有重要意義。由于高鐵通過能力的限制區間在大型客運站對應的虛擬區間，分析京滬高鐵所經過的車站可知京滬高鐵能力的限制點可能為濟南西站、南京南站和徐州東站等，由于篇幅有限，以徐州東站為例計算其對應的虛擬區間通過能力，徐州東站站場示意圖見圖26。

(1)基礎數據

以京滬高鐵徐州東站2018年5月某天下行方向接發的高鐵列車數據為例，各類高鐵列車數量為：本線列車105列，其中始發列車2列，終到列車4列，通過列車22列，僅停站列車69列，待避越行列車8列；跨線列車54列，其中“正接正發”列車38列，“反接正發”列車16列。

各種列車間隔時間見表1。

圖26 徐州東站站場示意圖

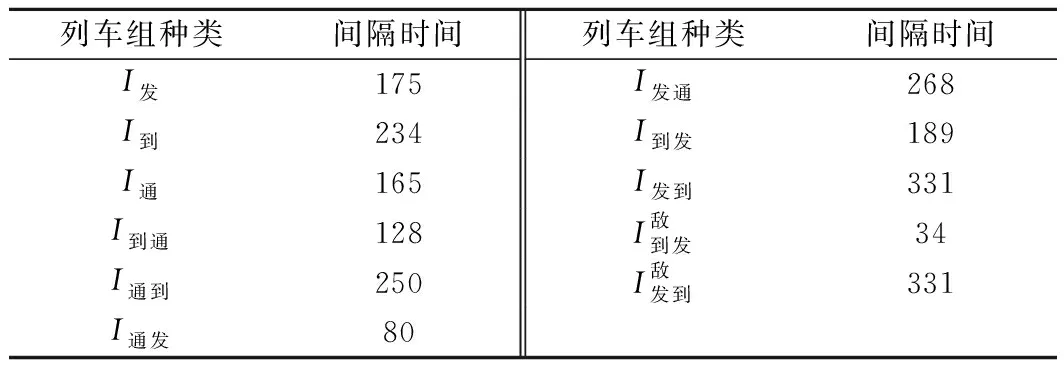
表1 各種列車間隔時間 s

各類列車停站時間為：本線列車3.11 min，“正接正發”跨線列車為4.74 min，“反接正發”跨線列車為8 min。

(2)計算過程

根據各列車數量可得出各列車出現概率：始發列車0.01，終到列車0.03，通過列車0.14，僅停站列車0.43，待避列車0.05；“正接正發”列車0.24，“反接正發”列車0.10。

根據第2節的各類列車組最小間隔時間與式(3)可得各類列車組的數量(存在四舍五入的情況)、各類列車組的最小間隔時間和各類列車組占用區間的時間，見表2。

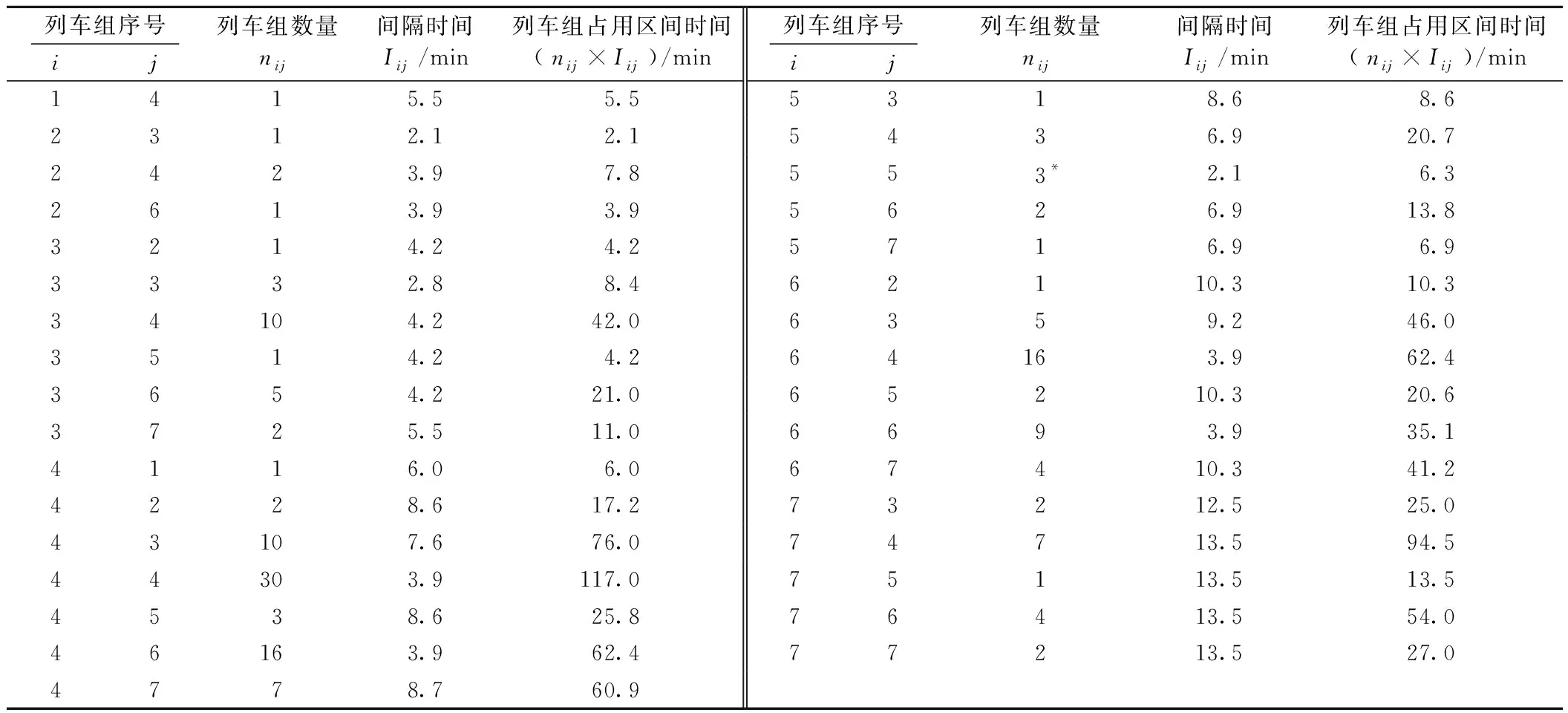
表2 列車組數量及其時間間隔

各方向跨線列車數為：鄭州方向到上海方向中“反接反發”為4列，“正接反發”為6列；鄭州方向到北京方向中“反接正發”為10列，“正接正發”為20列；北京方向到鄭州方向中“反接正發”為6列，“反接反發”為3列；上海方向到鄭州方向中“正接反發”為9列，“正接正發”為18列。取tki=1 min，則

根據徐州東站實際運營時間取f=0.7，由式(7)可得N通=163對，與實際運行159對相比，計算結果和實際情況較為吻合，說明計算結果比較準確可靠，同時也證明徐州東站通過能力利用率已經接近飽和狀態。

再依此方法計算濟南西站、南京南站等站的虛擬區間通過能力，選其中能力最小者即可求出京滬高鐵的通過能力；同理計算鄭州東站等站的通過能力就可求出鄭徐高鐵的通過能力。

4 結論

隨著我國高鐵網規模和客流需求的不斷擴大，對準確掌握和充分挖掘高鐵通過能力提出了更高的要求。本文提出將車站虛擬化的思想，通過構建車站的虛擬區間和相應列車的虛擬區間運行線，在平均最小列車間隔法的基礎上給出了高鐵通過能力的計算方法。現有計算高鐵通過能力的方法普遍存在著將車站和區間割裂、不考慮跨線列車、對高鐵能力缺乏進一步優化等問題，本文考慮了跨線列車對能力計算的影響、實現了車站與運行線的點線能力一體化計算，對于今后的高鐵能力優化問題，虛擬區間的運用可以使模型結構更加簡單，且將跨線列車也列入優化對象，使優化結果更加符合實際。