基于GA-BP的大壩滲透系數多目標反演分析方法

唐少龍，熊 威，萬小強，羅梓茗，萬思源，汪 慶

(江西省水利科學研究院，南昌 330029)

在水利工程滲流分析中，滲透系數的合理取值對工程滲流場的分布及滲透穩定評價至關重要。傳統滲透系數獲取方法主要通過鉆孔壓水試驗，由于受工程運行時間及人類活動等的影響，工程滲透系數在正常運行管理過程中會發生一定的變化[1,2]，無法適時掌握其變化情況。根據工程運行監測數據進行滲透系數反演成為當前重要途徑，其能夠經濟、快速的獲取實際滲透系數情況。

由于在大壩滲流過程中參數與效應量之間具有較強非線性特性，在對大壩多目標滲透系數反演過程中，采用傳統線性參數反演分析方法已經無法用于解決多目標滲透參數反演優化[3-5]。隨著計算機技術高速發展，越來越多的智能算法用于解決多目標非線性關系的預測，其中BP人工神經網絡運用最為廣泛。BP人工神經網絡以其強大的自學習和自判斷能力，能夠有效地解決滲流參數之間非線性關系的優化。如郭海慶、吳中如等利用連續型Hopfield神經網絡模型結合壩區現場實測資料對某堆石壩滲透系數進行有效反演[6]; 李守巨, 劉迎曦等根據滲流場的水頭觀測數據和注水試驗先驗信息，采用神經網絡反演了吉林白山水電站壩基及防滲帷幕滲透系數，得到了較高精度[7]；駱進軍, 李波等基于某拱壩原型觀測資料采用BP神經網絡對大壩壩基各巖層滲透張量情況進行了反演，并對結果進行了有效驗證[8]。然而，BP人工神經網絡在對樣本集進行訓練時，存在收斂速度不穩定、不能保證全局最優且拓撲結構不易確定的缺點，這些缺點將不利于BP人工神經網絡進行多目標滲透參數的反演。針對上述缺點，本文擬采用GA遺傳算法對BP人工神經網絡參數進行優化，構建最優BP人工神經網絡參數組合，達到加快計算速度并達到全局最優的目的。

本文以某黏土斜墻壩為研究對象，通過已構建GA-BP人工神經網絡模型，對某黏土斜墻壩各介質分區滲透系數進行了反演計算，并將反演結果與傳統BP人工神經網絡計算結果進行了比較驗證。

1 基于GA-BP的滲透系數反演分析方法

1.1 GA優化BP人工神經網絡

BP人工神經網絡訓練精度及速度與網絡結構層數、節點個數及初始權值和閾值有較大關系，當網絡結構層數、節點個數確定的情況，初始權值和閾值的合理選擇將對神經網絡訓練的好壞起決定性作用。針對最優初始權值和閾值參數組合確定難得的問題，本文通過GA遺傳算法對其參數組合進行尋優，獲取BP人工神經網絡結構中的最優參數組合，賦予最優參數組合的BP人工神經網絡具有較好動態自適應能力，能夠有效克服BP人工神經網絡收斂速度慢、不能保證全局收斂的缺陷[9]。根據GA遺傳算法及BP人工神經網絡的相關理論，本文通過MATLAB軟件實現GA對BP人工神經網絡權值和閾值的尋優過程，具體尋優步驟如圖1所示。

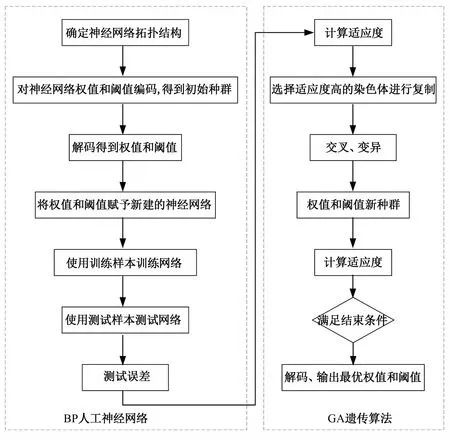
圖1 GA優化BP神經網絡流程Fig.1 GA optimization BP neural network process

1.2 滲透系數反演模型

本文在對大壩各介質滲透系數的反演計算時，采用正交設計、有限元穩定滲流正分析及GA-BP人工神經網絡相結合的反演方法。其中正交設計方法通過SPSS中的正交設計表從眾多參數組合中安排數目較少的參數組合用于有限元穩定滲流正分析，從而大大減少滲流正分析計算的工作量；有限元穩定滲流正分析是將正交設計參數組合代入大壩有限元模型中進行滲流數值模擬，生成BP人工神經網絡所需訓練樣本集；BP人工神經網絡通過有限元穩定滲流正分析所得訓練樣本集構建各介質滲透系數組合與相應效應指標之間的非線性映射關系模型，從而通過輸入效應指標實測值對滲透系數進行反演；由于BP人工神經網絡在訓練過程中誤差反向的傳播容易陷入局部最優值的特點，因此采用GA遺傳算法對BP人工神經網絡結構中的權值和閾值參數組合進行尋優，獲取最優的反演參數[10-12]。BP神經網絡網絡模型如圖2所示。

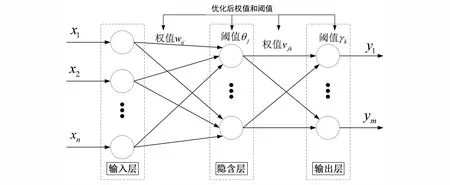
圖2 BP神經網絡網絡模型Fig.2 BP neural network model

1.3 滲透系數反演流程

本文所建立的GA-BP人工神經網絡多目標反演方法進行滲透系數反算的步驟如下：

(1)針對大壩實際結構分區情況，選取含有監測數據的剖面建立三維有限元模型用于進行滲流正分析。

(2)采用正交設計方法將待反演滲透系數在取值范圍內選取若干個水平，設計獲取相應的組合方案，并正交設計所得組合方案代入有限元模型進行穩定滲流正分析計算，獲得GA-BP人工神經網絡訓練所需的樣本數據集。

(3)以滲流正分析中測點壓力水頭為神經網絡的輸入層，壩體各介質的滲透系數為輸出層，建立大壩各測點壓力水頭與各介質滲透系數組合之間的非線性映射關系。

(4)將大壩滲壓計測點實測壓力水頭數據輸入優化后的BP人工神經網絡模型中，即可得到大壩所求各介質分區的滲透系數大小。

2 工程實例

2.1 工程概況

某黏土斜墻土石壩正常蓄水位55.00 m，校核洪水位57.14 m，總庫容2 069 萬m3，壩頂高程58.40 m，最大壩高19.8 m，壩寬6.0 m，壩頂長度667.0 m。為實時掌握了解工程安全運行情況，布置了較為齊全的滲壓監測設施。本文以最大壩高典型斷面處的壓力水頭觀測資料實測值對該壩滲透系數進行反演，典型剖面滲壓計布置在大壩建基面處，如圖3所示。

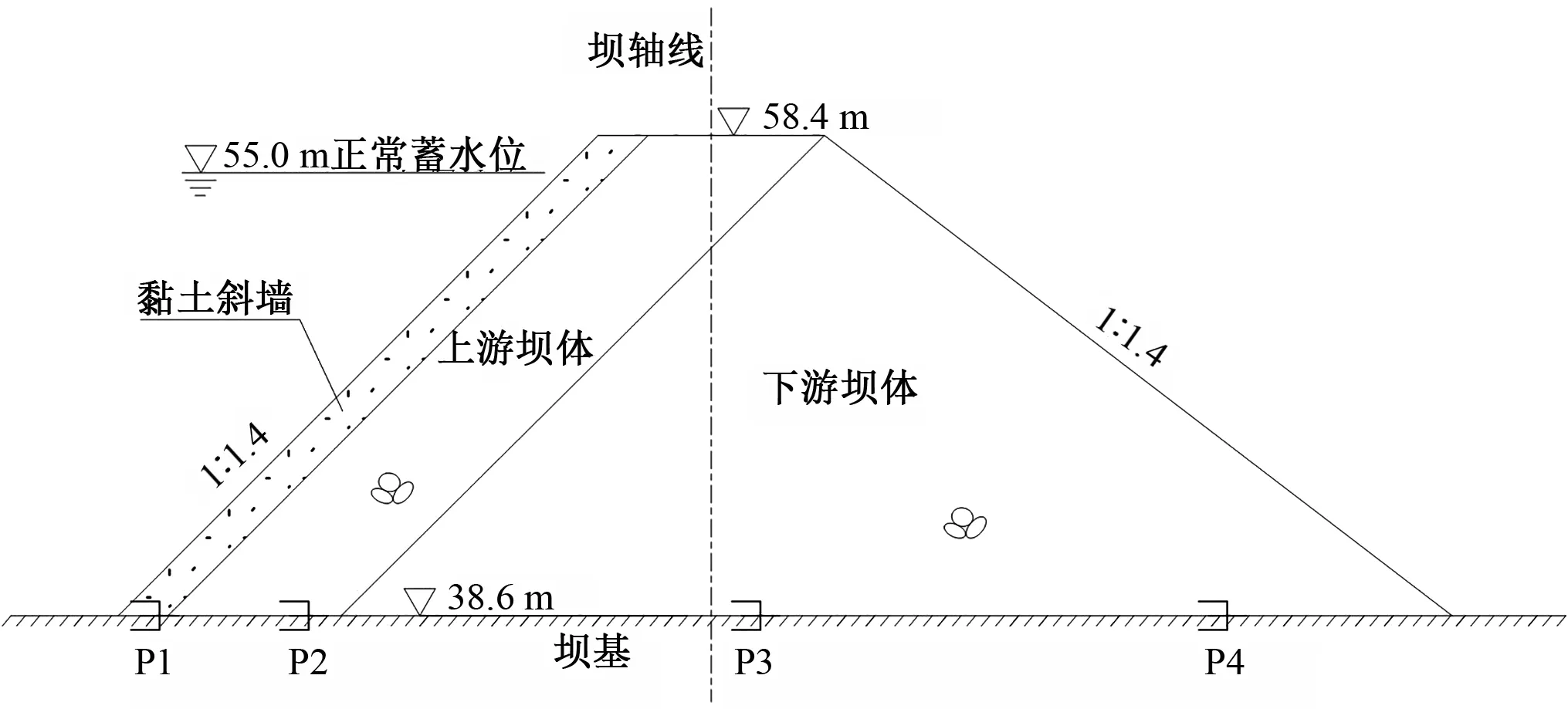
圖3 典型剖面滲壓計布置Fig.3 Osmometer arrangement of typical profile

根據大壩的實際情況，建立典型斷面三維有限元滲流模型，有限元模型計算范圍：上、下游以壩踵、壩址為界各取2倍壩高，建基面以下取1.5倍壩高，如圖4所示。模型采用六面體等參單元結合部分退化的四面體單元進行網格剖分，共劃分單元19 548 個，節點數22 451 個。

圖4 典型壩段有限元模型Fig.4 Finite element model of typical dam section

2.2 計算過程

查閱該壩初設數據并結合工程經驗，確定大壩黏土斜墻、上游壩體、下游壩體、壩基等介質滲透系數反演計算范圍，如表1所示。

表1 滲透系數取值范圍 m/sTab.1 Permeability coefficient range

BP神經網絡模型結構的穩定性受訓練樣本集的數量多少影響較為敏感，滲透系數正交設計取黏土斜墻、上游壩體、下游壩體、壩基4因素按5個水平作為正交設計輸入，輸出17個待反演參數的組合，各水平取值情況如表2所示。將正交設計所得組合代入有限元模型中進行穩定滲流正分析，獲取BP人工神經網絡所需的訓練樣本樣本集數據進行神經網絡訓練，其中P1～P4節點壓力水頭計算值為神經網絡輸入，大壩黏土斜墻、上游壩體、下游壩體、壩基等介質滲透系數取值為輸出。本次滲透系數反演過程中，不考慮上游水位變化的影響，上游水位取常值，為正常蓄水位55.00 m。

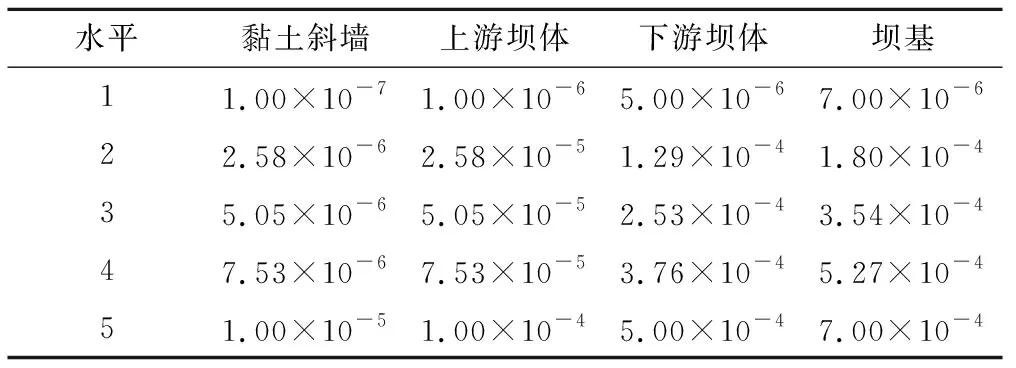
表2 基于正交設計滲透系數各水平取值 m/sTab.2 Value of each level of permeability coefficient based on orthogonal design

本文BP人工神經網絡結構中隱含層層數取為1，隱含層神經元節點數取值通過常用經驗公式進行試予以確定，經驗公式如下：

(1)

式中：L為隱含層節點個數；m、n分別為輸入層、輸出層節點個數；a為常數，取1～10。

本文m=4、n=4，經過反復試算，當L=9時預測效果綜合誤差最小。GA遺傳算法對BP人工神經網絡結構中權值和閾值進行尋優時，種群個數取40，最大遺傳代迭代次數取50，代溝取0.95，交叉概率取0.7，變異概率取0.01。

2.3 計算結果

利用滲壓計P1～P4實際所測壓力水頭監測數據代入訓練好的BP人工神經網絡模型結構，模型輸出數據即為大壩黏土斜墻、上游壩體、下游壩體、壩基等各介質分區的滲透系數反演結果，反演得到的各分區結果為K黏土斜墻=7.91×10-6m/s、K上游壩體=6.19×10-5m/s、K下游壩體=2.87×10-4m/s、K壩基=6.98×10-5m/s，通過觀察上述反演結果可知基于GA-BP人工神經網絡的多目標反演算法結果均處于相應的取值范圍內。

為進一步檢驗該反演所得各滲透分區滲透系數大小的合理性，將反演所得各滲透分區滲透系數代入有限元模型中進行穩定滲流正分析，獲取滲壓計P1～P4測點的壓力水頭計算值，并與實測值進行對比，結果如表3所示。由表3對比結果可得，滲壓計P1～P4測點壓力水頭計算值與實際測量值吻合較好，計算值與實測值之間相對誤差在0.6%～3.6%之間，由此說明基于GA-BP人工神經網絡的多目標反演算法得到的大壩各分區滲透系數合理、可行。

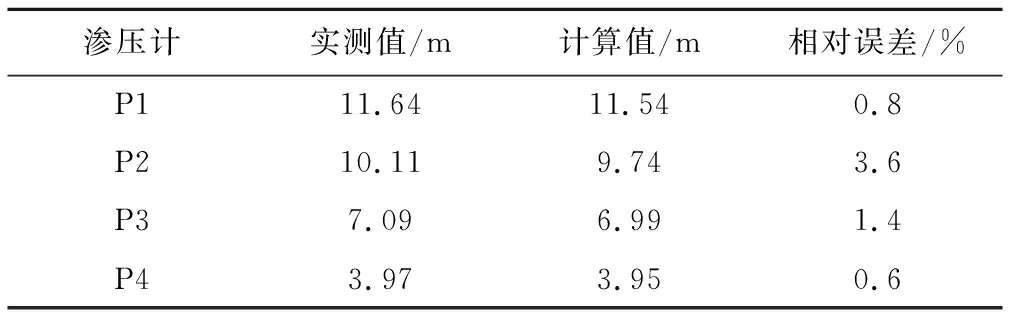
表3 滲壓計P1～P4測點壓力水頭計算值與實測值Tab.3 The osmometer P1～P4 measured the point pressure and the measured value

2.4 GA-BP與BP人工神經網絡計算結果對比

為比較GA-BP與BP人工神經網絡計算效果的，本文單獨采用不經GA遺傳算法優化的傳統BP人工神經網絡建立滲透系數反演模型對滲壓計P1～P4測點的壓力水頭進行計算，結果見表4。

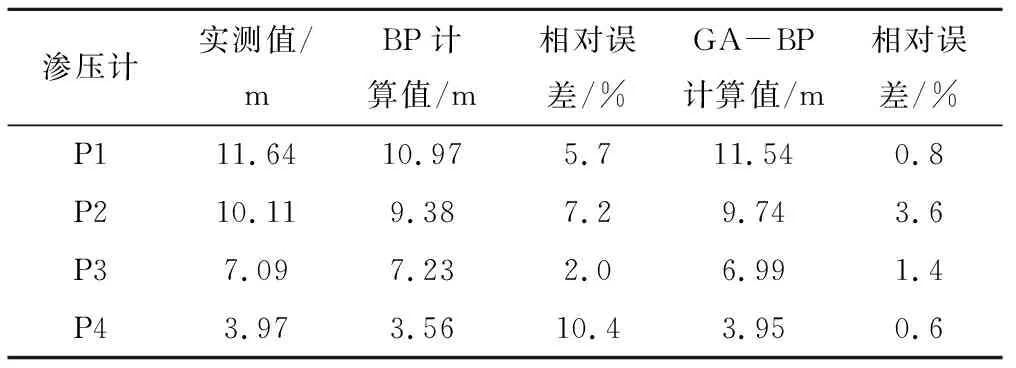
表4 基于BP神經網絡滲壓計P1～P4測點壓力水頭Tab.4 Based on BP neural network osmometer P1～P4 measuring point pressure

對比GA-BP與BP人工神經網絡計算結果可知：BP人工神經網絡計算P1～P4測點壓力水頭誤差范圍2.0%～10.4%，該方法計算結果整體前者反演精度更低。同時利用MATLAB自帶計時功能對上述兩種模型訓練時間進行對比，經過GA優化后的BP人工神經網絡對樣本進行訓練時間為0.48 s，后者訓練時間為1.14 s，顯然經過GA優化后BP人工神經網絡在訓練樣本數據集時收斂速度同樣優于傳統的BP神經網絡。

3 結 論

(1)針對BP人工神經網絡樣本數據集訓練收斂速度慢、目標值難以保證全局最優且結構不易確定等問題，引入GA遺傳算法對其尋優后，在收斂速度及計算精度上都將有所提升。

(2)基于測點壓力水頭監測數據，采用GA-BP多目標反演算法所獲得的各介質滲透系數，將其代入滲流正分析中得到的滲壓計P1～P4測點壓力水頭計算值與實測值相對誤差分別0.8%、3.6%、1.4%和0.6%，總體上與實測數據基本一致，表明GA-BP多目標反演算法合理可行，可望在水利工程其他參數反演領域進一步推廣。