改進的道格拉斯-普克算法在電信代維系統的應用?

周 騰 李曉妍

（1.中國科學院合肥物質科學研究院 合肥 230031）（2.中國科學技術大學 合肥 230026）（3.江蘇海事職業技術學院 南京 210000）

1 引言

隨著移動終端的飛速發展，GPS 技術的不斷進步，智能手機已成為一種非常普遍的設備［1］，廣泛應用于通信設備看護和通信線路巡檢中。在電信綜合代維管理系統中，這些智能設備能夠采集代維巡檢人員移動線路的GPS軌跡的經緯度信息，并通過4G 移動網絡傳輸到后端服務器中，系統會自動與預先設定的巡檢范圍進行適配，通過加強對代維巡檢人員的管控力，提高巡檢質量。同時，移動設備所采集到的GPS 經緯度信息也呈現出一種爆炸性的增長趨勢［2］，大量的數據不僅極大地影響了系統的存儲效率，占用了較多的運算資源，也影響了前端的瀏覽體驗。因此，研究如何將GPS經緯度信息進行壓縮存儲勢在必行，既從算法方面進行改進，一方面要能夠在軌跡保存完整的情況下，簡化軌跡數據，以提高存儲資源的利用效率；另一方面要通過壓縮數據，減輕運算復雜度，提高讀取效率，以改善前端展示時的用戶體驗。

2 GPS軌跡壓縮算法——道格拉斯-普克算法

軌跡數據壓縮算法一般分為兩類［7］，一是將運動軌跡進行分段線性化［3］，由于其算法形式簡單，計算復雜度低，是目前最為常用的算法；二是非線性的軌跡擬合［4］，如Bezier曲線，非線性擬合更接近真實軌跡，但是其算法復雜，計算量大。由于電信代維巡檢中的人員軌跡是沿電信線路或者巡檢道路而記錄的，所以使用線性壓縮算法更能夠貼合現實中的情況，而且也能夠節約一部分運算資源。在眾多線性壓縮算法中，道格拉斯-普克算法最具有代表性。

道格拉斯-普克算法（Douglas-Peucker Algorithm）［5］簡稱DP 算法，在1973 年由Douglas 和Peucker提出。該算法步驟如下：

1）在軌跡曲線首尾兩點A、B 之間連接一條直線AB，該直線為曲線的弦；遍歷曲線上其他所有點，求每個點到直線AB的距離，找到最大距離的點C，最大距離記為dmax；

2）比較該距離dmax與預先定義的閾值Dmax大小，如果dmax＜Dmax，則將該直線AB 作為曲線段的近似，曲線段處理完畢。

3）若dmax＞Dmax，則使C 點將曲線AB 分為AC和CB兩段，并分別對這兩段進行1）、2）步處理。

4）當所有曲線都處理完畢時，依次連接各個分割點形成的折線，即為原始曲線的路徑。

該算法結構簡單，效率相對較高［6］。但它是一種需要明確起點和終點的后壓縮方法，是一種離線壓縮方法。而在電信代維系統中，數據需要實時進行處理，DP 算法在代維系統這種場景中并不能有效適用。因此，需要對該算法進行改進，使其能夠對這些數據進行實時壓縮處理。

3 改進的道格拉斯-普克算法

3.1 軌跡采集方式改進思路

DP 算法是一種離線后壓縮算法，需要明確知道曲線的起點和終點，而代維系統中的GPS軌跡記錄是實時傳輸數據，需要一種在線實時的壓縮算法，因此，需要在DP算法的基礎上進行改進。

由于代維系統中線路巡檢的軌跡是有折返的，實時數據量龐大，因此算法改進時需要考慮以下三個問題。

其一，相同經緯度的記錄點冗余問題。當巡檢遇到設備檢查點時，巡檢人員會在此處停留，軌跡偏移量便會大大減少，甚至會出現多次上報的數據經緯度值相同的情況，造成大量數據冗余。這部分數據若是運算后再進行剔除，會加大計算資源的耗損［7］，因此應在運算前進行預處理比較篩選，減少計算量。

其二，計算模型問題。地理空間距離的計算中含有大量的三角函數運算［8］，對計算資源的消耗較大。一般來說，地球上兩點之間的距離計算有以下兩種模型［9］：一是球面模型。這種模型將地球看成一個標準球體，球面上兩點之間的最短距離即為圓弧長，這種方法使用較廣，邏輯相對簡單，消耗的CPU 計算資源較少。二是橢球模型［9］。這種模型最貼近真實地球，精度較高，但計算較為復雜，需要耗費更多的CPU 運算資源［10］。根據電信巡檢業務需求特點，對GPS 軌跡精度并無高精度要求，因此應采用球面模型來計算地理空間距離以減少運算資源的消耗。

其三，共線軌跡點記錄存留問題。因軌跡是有折返的［11］，即出現三個GPS軌跡點在同一條直線上的情況，則需要對三點共線的情況進行討論，如果巡檢方向一致，應該舍棄位于中間的點；如果巡檢線路出現折返，則必須全部保留。這樣既能保證軌跡完整性，又能夠有效減少數據冗余。

因此，改進的DP算法步驟如下：

1）將GPS 軌跡記錄上的某一點記為第一點A，與相鄰的下一個記錄點進行比較，若兩點經緯度數據完全一致，則刪除下一點的記錄，再將A 與下一個記錄進行比較，依次篩選，排除經緯度數據完全相同的冗余點，直至記錄點與A 經緯度數據不同，記為點B。

2）按照步驟1 的方法，找到與點B 經緯度數據不同的記錄點C。

3）在AB 之間連接一條直線，計算點C 到直線AB的歐式距離d。

4）若距離d=0，則A、B、C 三點共線。根據經緯度信息，判斷C 點是否位于A、B 兩點之間，若是，則保留C點數據；若否，則刪除B點數據。

若距離d 小于閾值，則刪除C 點數據。重復步驟2），尋找下一C點。

若距離d 大于閾值，則保留C 點數據。將記錄點B作為第一點，重復步驟1）、2）、3）、4），直至工單記錄結束。

3.2 GPS軌跡兩點間距離的計算優化

在軌跡記錄距離計算時，有大量的三角函數計算，占用了較多計算資源，影響系統運行速度，因此對此進行計算優化。

根據球面計算模型，在GPS軌跡上有任意兩點A、B，設φ1、φ2為AB兩點的緯度，ω1、ω2為兩點的經度，R為地球球面模型的半徑，Δω、Δφ分別為AB兩點的經、緯度差，這兩點的圓心角σ 可通過球面余弦定理［12］得出：

根據弧長公式可得A、B 間的球面距離：d=Rσ 。如果A、B 之間距離很短，即d 相對于R 很短時［13］，A、B 間的圓心角很小，cos Δω余弦函數無限趨近于1［9］，那么上述的反余弦函數就會出現較大的舍入誤差。為避免這種情況的出現，利用正弦函數的haversine 公式來進行公式變形計算地球表面距離。這樣即便距離很近值很小，也能保持足夠的有效數字。

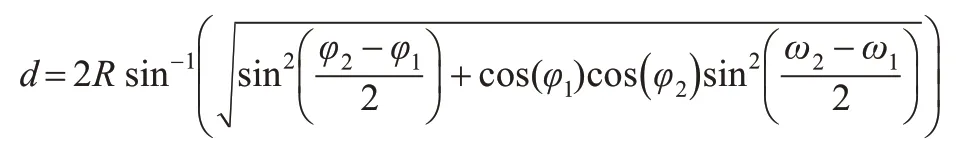
在實際應用中，GPS 軌跡記錄采集的密度較高（30s/次），而代維巡檢人員的行走速度不會超過20km/h，因此，可以認為經緯度偏移值較小即

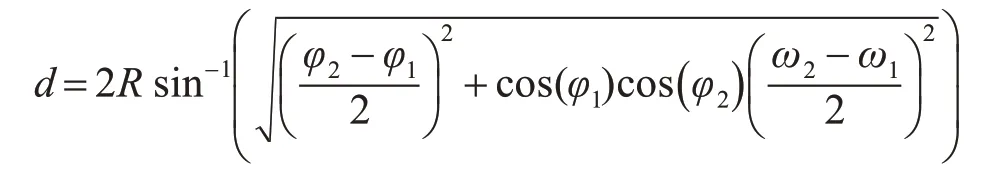
3.3 偏移值d的計算

根據上述內容，GPS 軌跡記錄會出現記錄點共線的情況，要對此進行判斷。因此，需要分別計算AB、AC、BC 的距離。為避免三角函數運算，本研究采用海倫公式［14］，根據三點構成的三角形來計算歐式距離d。設S 為三角形ABC 的面積，AB 為底，d 則為三角形的高。根據三角形面積公式，可知：d=海倫公式如下所示：

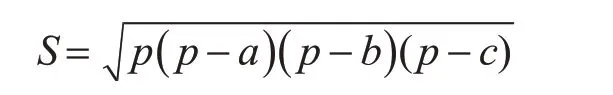
其中，a=AB，b=BC，c=AC，p 為三角形的周長的即

因此：

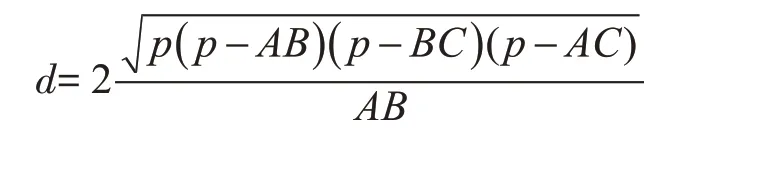
4 算法實驗與仿真

本研究對改進后的算法進行數據檢驗。從數據庫中隨機抽取了30s采集一次的500條線路巡檢工單，共計25231 條記錄作為測試數據，利用面向對象的python語言對算法進行編程。

4.1 壓縮比測試

對上述工單進行壓縮處理。選取4 個閾值進行比較。壓縮比如圖1所示。

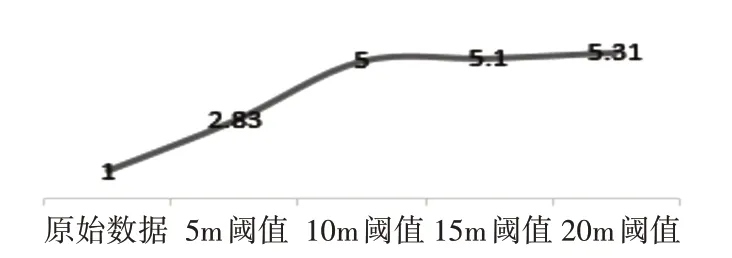
圖1 不同閾值下的壓縮比

可見，運用改進的DP 算法，在閾值為20m 時，壓縮比取得了非常良好的壓縮效果，壓縮比達到5.31，若實際應用到系統中，將大大減少工單記錄數據量，減輕存儲壓力［15］，提高存儲讀取效率。

4.2 壓縮軌跡展示示例

選取一條有85 條記錄的工單，并采用5m、10m、15m、20m 四種閾值進行壓縮處理，處理后軌跡如圖2～6所示。

圖2 原始軌跡記錄（30s/次采集）

圖3 采用5m閾值處理的軌跡

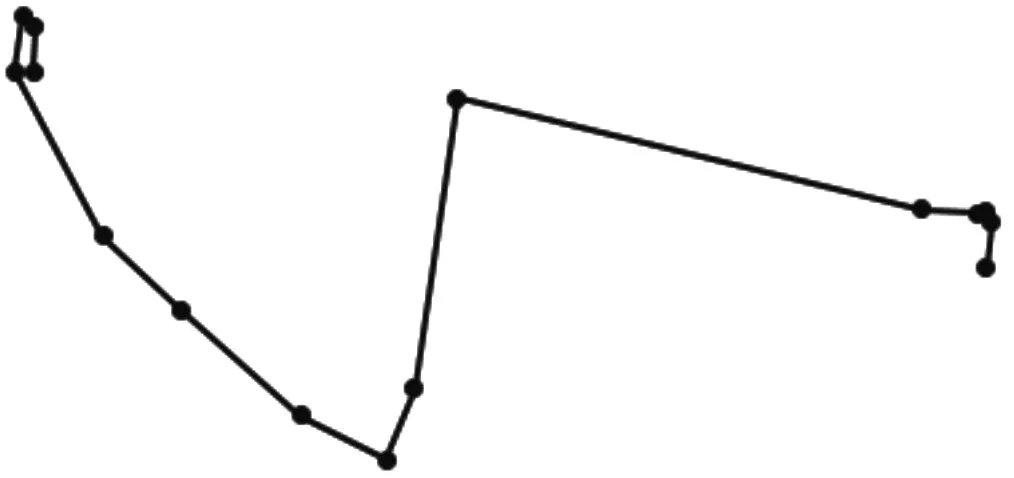
圖4 采用10m閾值處理的軌跡

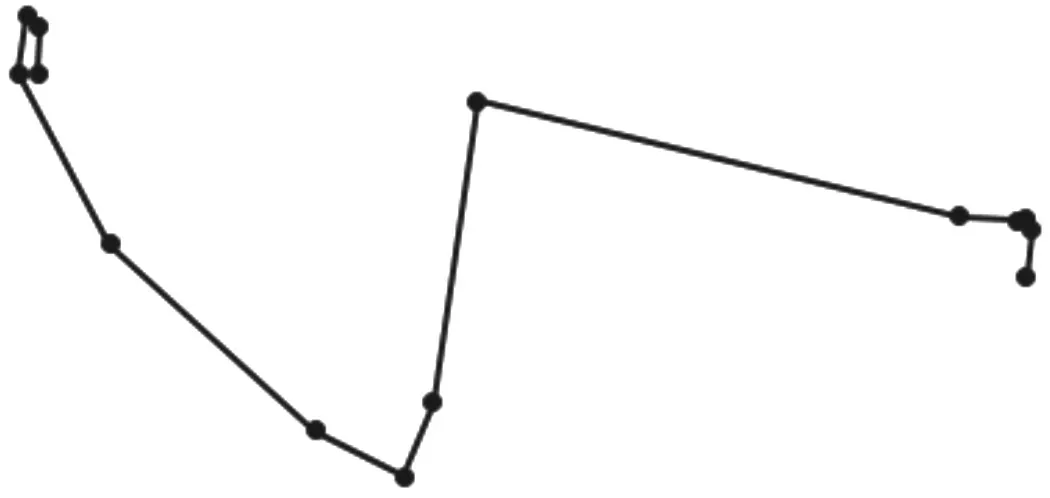
圖5 采用15m閾值處理的軌跡

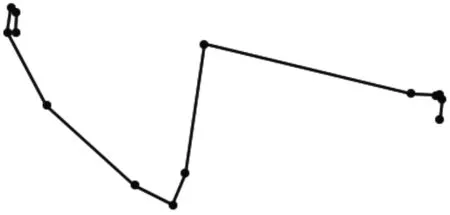
圖6 采用20m閾值進行處理

可見，在不同的閾值下，線段的基本都能夠清晰保存GPS 軌跡記錄，且隨著閾值的擴大，線段化的明顯越來越明顯。仿真實驗證明能夠滿足線路巡檢業務的需要。

5 系統應用

經過仿真實驗結果和業務中精度的需求的綜合考慮，在江蘇移動綜合代維系統中進行實地應用。運用改進的DP算法，采用10m作為閾值，對工單進行處理。首先對2018年8月的數據進行處理，并與原數據進行離線后比較。經比對，8 月GPS 軌跡記錄數據量可減少70%，前臺加載渲染速度提高近50%，達到了較為預期滿意的效果。此后，又將此算法應用到2018 年9 月數據的實時處理中。同比數據量下降77%左右得到的相對滿意的效果。

6 結語

本研究采用了改進后的DP 算法，對GPS 軌跡記錄進行壓縮，使其適應電信業務中的實時壓縮要求，并進一步討論了節約運算資源并提高運算速度的方法。經過實驗測試，證明該算法能夠在提高壓縮比的情況下，滿足軌跡展現管理的要求。通過這一算法，能夠顯著減輕服務器的存儲和渲染負擔［16］，進一步提升了用戶體驗。本研究對電信人員巡檢軌跡和看護軌跡的壓縮和存儲方面有一定的參考價值。