基于A*初始解的禁忌搜索算法優化及仿真應用?

劉婷婷 高 尚

（江蘇科技大學計算機學院 鎮江 212003）

1 引言

無人駕駛汽車在某種性能參數的作用下，索引一條自起點至目標終點的最優級、次優級無碰路徑，這種技術被人們稱作路徑規劃［1］。工作實踐中，單點搜索算法極易陷身局部最優的狀況，禁忌搜索算法的出現，為求解車輛路徑問題提供了新的工具［1］。禁忌搜索算法簡單易于理解，程序容易實現，運行所需時間較短，禁忌表的約束使算法不易陷入局部極小，在無人駕駛汽車的路徑規劃技術中，這種算法已然引發了相關科研工作者地高度關注。本文針對現有研究中原禁忌搜索算法大多采用有向邊排列的解作為表示方法來構造算法，這樣的解的表示不夠直觀，算法策略表現復雜使人難以理解，搜索效率低和收斂速度慢等缺點。提出了引入A*算法確定初始解的改進措施，通過簡化解的表示方法來提高其求解路徑規劃問題的全局尋優能力。在柵格地圖法中，通過對其他智能算法的仿真實驗表明，改進的禁忌搜索算法全局尋優能力提高，且具有更快的收斂速度和更高的尋優精度。

2 禁忌搜索算法

2.1 禁忌搜索算法基本原理

禁忌搜索算法（Tabu Search，TS）技術是一種在局部鄰域搜索的基礎上進行擴展的亞啟發式搜索技術，是一種逐步尋優算法［2］。局部鄰域搜索是在貪婪思想的基礎上，對當前解的鄰域進行搜索，這樣的搜索方式使得鄰域的結構和初始解的選取決定了其性能的優劣［3］，這樣的搜索結果容易陷入局部極小而無法保證全局最優。而禁忌搜索算法李用一個禁忌表將已經到達過的局部最優點記錄下來，并在下一次搜索過程中有選擇的避免重復搜索這些點［4］，以此跳出局部最優點［5］。這好比人類的短期記憶，人們不會重復或者有選擇的重復剛剛走過的路；同時“遺忘”又使這些禁止在一段時間后失效，最終達到全局優化的目的［3］。

該算法可以簡單地表示為

STEP1 選定一個初始解Xnow；令禁忌表H=ф；

STEP2 若滿足終止準則，則中止計算；否則在Xnow的鄰域N（Xnow）中選出滿足禁忌要求的候選集Can-N（Xnow）；

STEP3 在Can-N（Xnow）中選定一個評價值最好的解Xbest，令Xnow=Xbest，更新禁忌表H，重復STEP2；

STEP4 輸出計算結果，停止。

2.2 禁忌搜索算法的改進

禁忌搜索算法作為一種啟發式隨機搜索算法，確定初始解對算法的優化至關重要。1968 年發明的A*算法就是把啟發式方法如BFS，和常規方法如Dijsktra 算法結合在一起的算法。A*算法計算敏捷，雖然無法保證尋求最佳路徑，A*卻一定能夠找到一條最短路徑［6］。以這樣的解作為初始解可以保證優化算法的高效運行。

假設：將局部范圍內路面視為一個第一象限坐標圖，已知單位長度為1，以任意點為原點，車輛可向任意方向移動，求網格中任意兩個給定坐標之間的最短路徑。若將已知的坐標距離改為路徑上的障礙物或其他代價參數，例如，路段擁擠、路面限行或者交通事故等因素及其組合，就相當于求任意兩點之間繞過障礙物且有最短路程或最少等待的通路。

輸入：圖G=｛（x，y）|x＞0，y＞0｝有一個元定點s和會定點t，障礙物點B，以及每個相鄰單位之間路徑代價C。

輸出：G中從S到T的最短路徑的長度。

初始化階段：

STEP 0：運行A*算法得到一條最短路徑，設為初始解。元定點s標記為永久標記Y，對初始解路徑上點做臨時標記L，令禁忌表為空。

搜索階段：

STEP 1：將與永久標記Y 相鄰的5 個帶有臨時標記L 的坐標n，按f（n）=g（n）+h（n）做新的臨時標記L。g（n）表示從帶有標記Y 的點到任意點n 的代價，h（n）表示從點n 到路徑上與標記Y間隔為5的會定點t的評估代價。

在柵格地圖中：

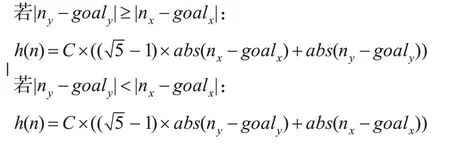
計算其最短距離，并將最小點標記為永久坐標Y。

STEP 2：更新禁忌表及當前最優解的記錄。

STEP 3：判斷f值是否為最小，且路徑不經過障礙物，如果是，則f 值在沿著該路徑進行時數值恒定。如果否，則將要進行的路徑上的f 值均大于恒定f 值。若已經具備最佳f值的結點，算法忽略f 值較高的節點的路徑，則刪除。重讀第2步和第3步，直到取得最優解。

3 數值仿真與分析

3.1 環境建模

為了驗證改進后的算法是否在路徑規劃問題中得到有效應用，本文采用對環境描述較為直接，且容易表示與修改的柵格地圖法。設計一個25×25 規模的二維柵格環境模型，每個柵格單元的大小為4m×4m，如圖1 所示，黑色區域代表的是未經膨脹處理的障礙物，其余灰色區域表示沒有障礙。并將質點以圈狀表示汽車的一定體積，保障規劃路徑與障礙物之間的安全距離。應用改進后的禁忌搜索算法完成從a 點到b 點的安全路徑規劃，同時還與初始解A*算法（如圖1）、人工魚群算法、蟻群算法以及粒子群算法的仿真結果進行對比分析。

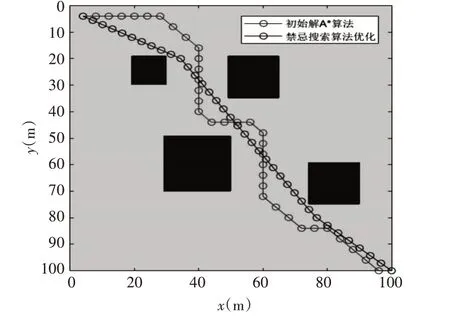
圖1 TS-P算法與初始解A*算法對比圖

3.2 初始參數設置

應用經驗試錯法，設置改進禁忌搜索算法（TS-P）；蟻群優化算法（ACO）的功能則是參考文獻編程實現［7］；粒子群優化算法（PSO）的功能參考文獻實現［8］；魚群尋優算法（AFSA）的功能則是參考文獻的內容編程實現［9］。

3.3 有效性分析

仿真實驗的軟件平臺是Matlab 2017，硬件平臺是Windows10的64位操作系統，2.53GHz的主頻，4G 的運行內存與Core i5 的處理芯片。各算法所規劃的路徑效果如圖2 中各曲線所示，并將各算法分別運行32 次，統計各算法的平均路徑長度（去掉最長路徑與最短路徑）和平均耗時，結果如表1所示。

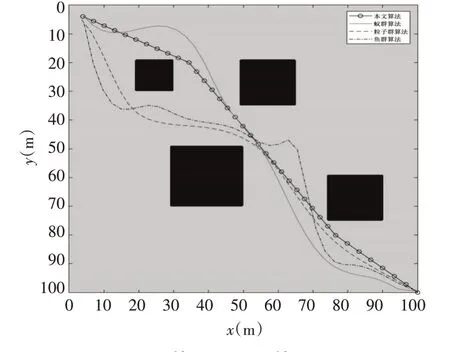
圖2 TS-P算法與其它算法對比圖

仿真結果顯示：A*算法運算時間為0.076，求的距離為164m，采用優化后的禁忌搜索算法，將A*得到的結果作為禁忌搜索的初始值，經過10 次迭代，路徑距離為138.49m。其迭代過程如圖3 所示，改進后的ST-P 算法經過6 次迭代即可找到最短路徑，收斂速度非常快，尋優性能極高。

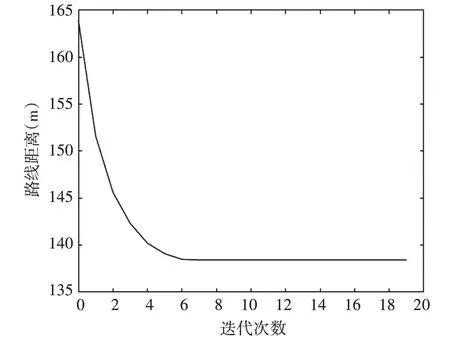
圖3 TS-P算法迭代過程圖

由圖1、圖2以及表1可知，初始解A*算法和粒子群算法及魚群算法雖然較高的時效性，但其規劃出的路徑過于曲折并且路程較長；而改進后的禁忌搜索算法（TS-P）和魚群算法（AFSA）的路徑比較光滑且長度短，兩種算法在時效性方面相差不大，但優化后的TS 算法的路徑長度方差明顯小于AFSA算法，說明優化后的算法穩定性好。

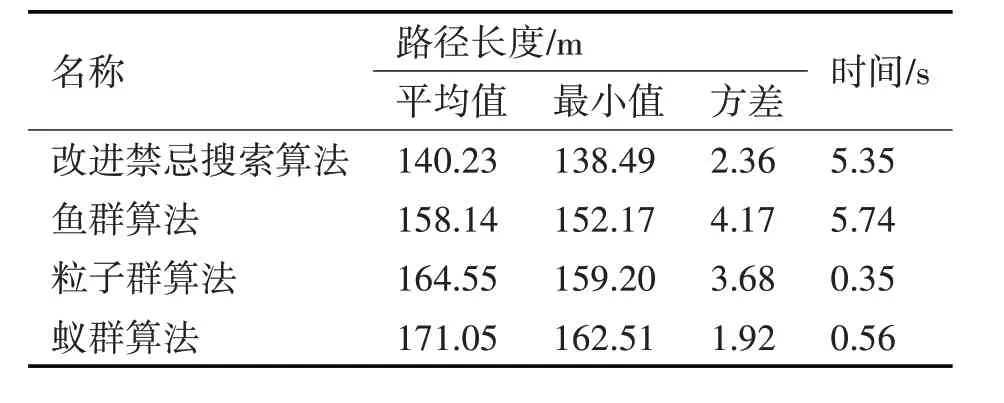
表1 各個算法計算結果統計表

4 結語

禁忌搜索算法是局部搜索算法的擴展，其特點是采用了禁忌表來避免重復前面的工作。相較于其他群智能算法，禁忌搜索算法用一個禁忌表記錄下已經到取得的最優解，并且利用禁忌表中的信息必變重復搜索之前的點，簡化計算。TS 算法原理簡單，計算速度快，易于實現。本文針對原有算法在解決路徑規劃問題時采用的解的表示方法不夠直觀，算法策略表現復雜使人難以理解、計算難度大、收斂速度較慢等缺點，提出引入A*算法確定初始解的改進措施，通過簡化解的表示方法來提高其求解路徑規劃問題的全局尋優能力。仿真實驗表明，與參考文獻中其他智能算法相比，改進后的TS算法在路徑規劃實例中計算速度和精度都有很大的提高，可用于解決汽車局部路徑規劃問題的實用高效的智能方法，本文算法有效、可行。