基于MapReduce 的模糊K-means 算法并行化研究?

楊延慶 袁華兵

（西安醫學院信息技術處 西安 710021）

1 引言

數據挖掘是一種決策支持過程，是指從大量數據中自動搜索出隱藏的具有特殊關系性并存在潛在價值的信息的過程，對科學研究和商業決策起著重要的作用。

聚類分析融合了統計學的思想，能夠衡量不同數據源間的相似性，把數據源分類到不同的簇中，是數據挖掘中重要的一個分支。K-means 算法是一種常用的聚類算法，該算法認為簇是由距離靠近的對象組成的，根據數據對象與各個簇中心的距離將其賦給最近的簇。K-means 算法是一種硬聚類算法，該算法定量描述了數據對象間的親疏關系，數據對象與簇的隸屬關系只有0 和1 兩個值，即每個數據對象僅屬于一個簇。但是，在現實生活中，很多事物間的關系是很難明確的，以天氣為例，晴天和陰天的界限是很難分割的。

模糊K-means 算法通過引入模糊理論［1］建立樣本對象類屬的不確定性描述，能夠比較客觀地反映現實世界中數據對象的親疏關系，具有重要的理論與實際應用價值。然而，在數據呈爆炸式增長趨勢的今天，從海量數據中進行挖掘，傳統的聚類算法逐步暴露出時間、空間等多方面瓶頸。高效地執行計算與海量可擴展存儲已迫在眉睫。

MapReduce編程模型［2］是Google提出的利用集群來處理大規模數據集的并行計算框架，Hadoo［3］是Apache基金會開發的一個分布式系統架構，其開源實現了MapReduce 計算模型。Hadoop 通過組織一定規模集群，構建分布式平臺對大規模數據進行計算和存儲，成為目前主流的云計算技術平臺［4～5］。文獻［6～8］中，作者基于MapReduce 編程模型，對K-means聚類算法的并行化進行了深入研究，并對并行算法的性能給出了詳細的闡述。國內外很多學者都在Hadoop 平臺上對其他多種數據挖掘算法進行了并行化研究［9～12］。

本文在基于Hadoop 的分布式計算平臺上，研究了模糊K-means 算法的MapReduce 模型并行化實現，并進行了相關試驗。

2 模糊K-means聚類［13］

設X={x1,x2,x3,…,xn}是含有n 個對象的待聚類樣本集合，其中，每個樣本對象xi有t 個屬性，xi={xi1,xi2,xi3,…,xit}。將對象樣本集和X 劃分為K 個簇{c1,c2,c3,…,ck}，設uji為樣本對象xi對于第j 簇類的隸屬度。K-means 聚類算法中，隸屬度函數uji={0,1}，樣本對象xi對于某一簇類的隸屬度只有0和1，這是一種硬聚類算法，其主要依據是“類內誤差平方和最小化”準則。在uji={1} 情況下，xi對第j 個簇類隸屬度為1，而對于其他簇類的隸屬度全為0，xi與其他簇類間的一些隱藏關系K-means算法無法給出描述。

在模糊K-means 算法中，提出了“類內加權誤差平方和最小化”準則［4］，一個對象樣本可以屬于多個簇類，令uji∈[0,1],i=1,2,…,n,j=1,2,…,k，即給予對象樣本xi一個與簇類距離成反比的一個非絕對0，1 的加權隸屬函數，且滿足任一個樣本對象對于各簇類的隸屬度之和為1。

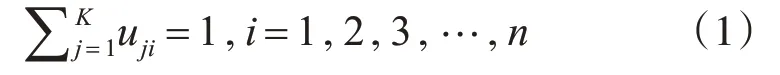
定義目標函數為

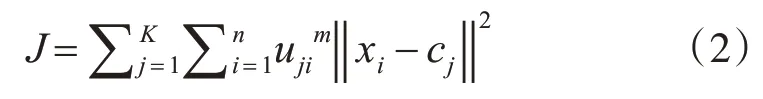
其中，m 為模糊指數，決定了聚類結果的模糊程度，通常取2。

使得目標函數式（2）達到最小值min(J)，根據約束條件式（1），對cj和uji求偏導，得到最優解：

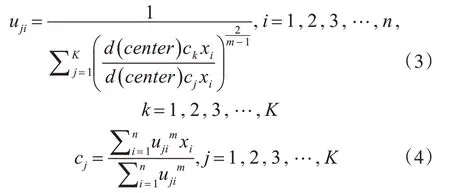
模糊K-means算法的主要步驟如下：

1）初始化簇類中心；

2）初始化對象樣本對簇類的隸屬值；

3）重復執行以下步驟，直至隸屬值收斂或達到迭代次數。

（1）根據式（4），計算新的簇類中心；

（2）根據式（3），計算每個對象樣本對于各簇類中心的新的隸屬函數值。

3 基于MapRecude的模糊K-means并行算法

3.1 MapReduce模型

MapReduce 采取“分而治之”的編程思想：把大規模的計算任務分解成若干個子任務，各子任務在集群中各分節點分別執行，然后整合各節點的中間結果，得到最終結果。簡而言之，MapReduce 就是“任務的分解與結果的匯總”［14～17］。MapReduce 計算過程分為Map（映射）和Reduce（規約）兩個階段，前者負責子任務的執行，得出中間結果，后者負責匯總中間結果。

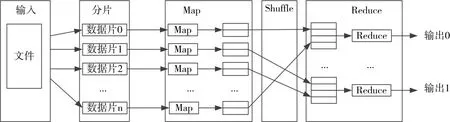
圖1 MapRduce運行機制

在輸入階段，一個大的輸入文件被劃分為若干個較小的文件塊；在M 階段，指派多個Map 并行計算分解后的數據塊，得到一系列中間結果；Shuffle階段，對各節點Map 的輸出進行分割重組，以減少帶寬的不必要消耗；R 階段獲得重組后的數據，進行相關計算，得到最終結果。圖1 描述了MaRduce的運行機制。

3.2 模糊K-means并行算法

模糊K-means 算法的MapReduce 模型并行化實現的基本思路：串行算法的每一次迭代計算，相應地啟動一次MapReduce任務，完成對象樣本與聚類中心的隸屬度計算和新的聚類中心。圖2 描述了一次MapReduce任務的算法流程。

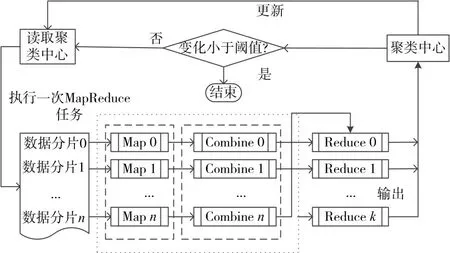
圖2 并行化模糊K-means算法的一次MapReduce任務

3.2.1 Map函數任務分析

Map 函數主要是讀取被分配的對象樣本和上一次迭代過程產生的聚類中心（或第一次初始化的聚類中心），由式（3）和式（4）計算對象樣本與各聚類中心的隸屬度uji以及用于計算新的聚類中心的臨時變量

3.2.2 Combine函數任務分析

Combine 函數相當于一次本地的Reduce 規約操作，Combine 函數的設計思路為：本地節點Map函數的輸出傳遞給其他節點的Reduce 函數之前，對Map 函數輸出的相同key 值的隸屬度uji和臨時變量進行一次“聚類中心預計算”過程，在不影響最終結果的條件下，將具有相同key 值的對合并，可以減小節點間傳輸開銷。

3.2.3 Reduce函數的設計

Reduce 函數的任務是獲取多個Map 函數輸出的中間結果計算出新的聚類中心，做為下一次MapReduce 任務的輸入聚類中心進行后續迭代計算。Reduce函數的偽代碼如下：

輸入：LongWritable key，Iterator＜LongWritable key，DoubleArray point＞values

輸出：Context context

4 實驗設計與結果分析

4.1 實驗環境與實驗數據

實驗環境為由8 臺主機搭建的Hadoop 分布式集群，包括1 個主節點（NameNode）和7 個從節點（DataNode），主節點控制集群文件系統的命名空間和客戶端的訪問控制，以及任務分配，從節點負責管理具體作業子任務的執行（包括啟動和監控作業、獲取其輸出，以及通知主節點作業完成）。各節點具有相同的硬件和軟件環境配置。硬件配置：處理器：Intel（R）Pentium（R）D CPU 3.00GHz，內存：2.00GHz，硬盤：160G；軟件環境配置：操作系統Ubuntu 12.04，Hadoop 版本：hadoop-1.1.1，JDK 版本：JDK1.6.0_30。串行算法單機測試環境具有集群單節點相同的硬件和軟件環境配置。

實驗中為了考察并行模糊K-means 算法在Hadoop 集群中處理不同規模數據集時的性能，采用Matlab 中的隨機函數生成了如表1 所示的五組小規模數據集和表2 所示的兩組較大規模數據集，其中每條記錄15維。

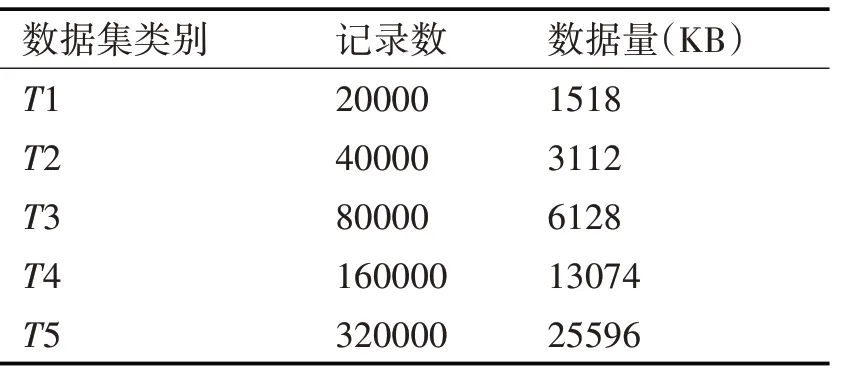
表1 小規模數據集

表2 較大規模數據集

4.2 結果分析

4.2.1 單節點性能比較實驗

為了驗證模糊K-means 算法在單個節點的集群中并行處理和單機環境中處理同一規模數據集的執行情況，選用數據集為T1，T2，T3，T4，T5，分別測試單機環境完成計算的消耗時間t1 和節點數為1 的集群環境完成計算的消耗時間t2，實驗中初始聚類中心隨機產生，最大迭代次數設為10，收斂閾值設為0.01。實驗結果如表3所示。

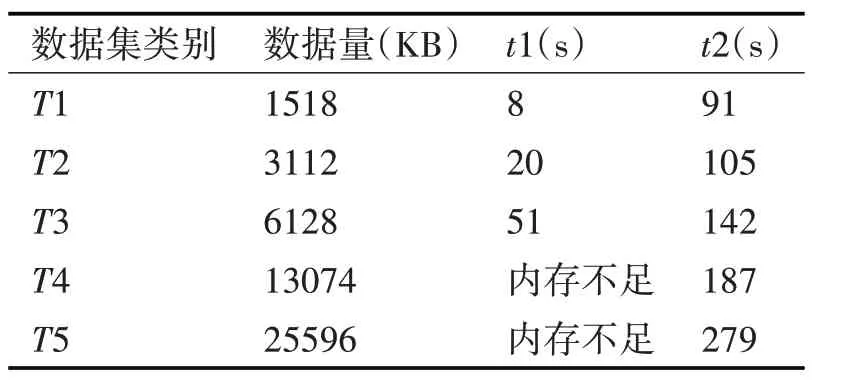
表3 單節點實驗結果

實驗表明，輸入數據集規模很小時，單機串行計算效率遠遠高于Hadoop 集群節點并行算法，主要原因是Hadoop 集群中用于實際計算的資源只占了總體消耗中很小的一部分，大部分資源被MapReduce 任務的啟動和交互所消耗。隨著輸入數據集規模逐漸增大，單機串行計算就會出現內存不足，計算任務終止，而Hadoop 集群能夠順利完成計算任務，且計算速度未明顯降低。這一點體現了基于MapReduce 的并行模糊K-means 算法在Hadoop平臺上具有處理大規模數據的能力。

4.2.2 集群加速比性能實驗

為了驗證集群節點增加時，對相同規模大小的輸入數據集，系統的處理能力。選用數據集為T6，T7，分別測試節點數為1，3，5，7 時，集群完成計算所消耗的時間，實驗中初始聚類中心隨機產生，最大迭代次數設為10，收斂閾值設為0.01。集群處理時間結果如圖3所示。

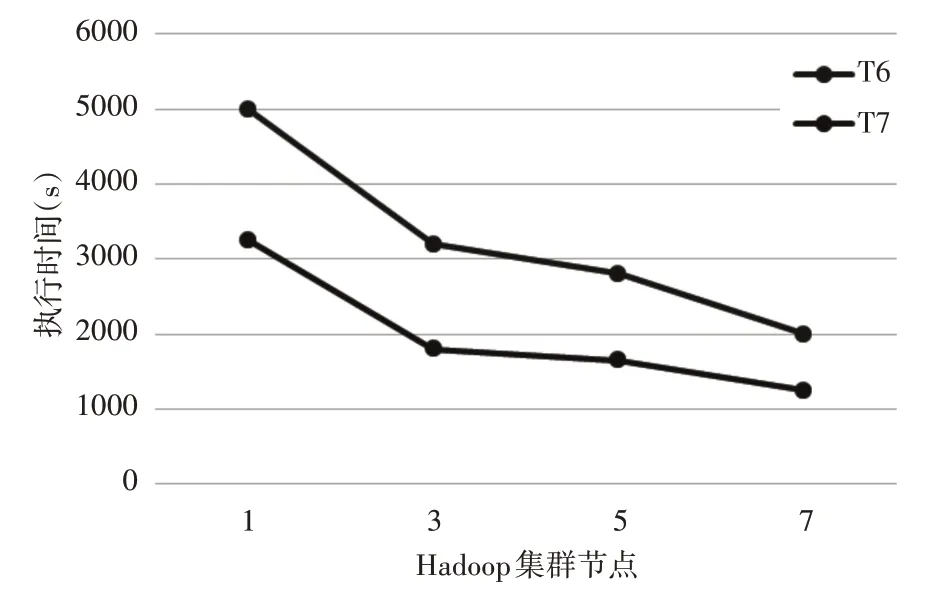
圖3 集群多節點處理時間

實驗表明，隨著節點的增加，Hadoop 集群處理輸入數據集T6，T7的執行時間逐漸減少，增加節點可以提高集群處理相同規模數據集的計算能力，并且在相同節點數下，處理數據集規模增加1.6倍時，執行速度提高了約1.9 倍。這說明基于MapReduce的并行模糊K-means 算法在Hadoop 集群中具有良好的加速比。

5 結語

為了提高模糊K-means 算法對大規模數據的聚類能力，本文通過在Hadoop 分布式計算平臺上對模糊K-means 算法的MapReduce 并行化進行了研究和實驗，實驗表明：模糊K-means 算法MapReduce 并行化后，應用在Hadoop 分布式集群中，提高了模糊K-means 算法對大規模數據的處理能力和計算效率，而且具有良好的加速比。