基于雙重目標的樹枝形專用線取送車優(yōu)化
李 冰,張志寧
(鄭州大學 管理工程學院,河南 鄭州 450001)
0 引 言
樹枝形專用線是鐵路樞紐內(nèi)常見的一種鐵路聯(lián)絡(luò)線布置形式,其特點是小運轉(zhuǎn)列車連掛本地車組到達裝卸站并完成取送作業(yè)后可直接前往下一裝卸站而不必返回編組站,樹枝形專用線取送車作業(yè)中,各裝卸站貨車入線時刻不同,但取回編組站內(nèi)時刻相同[1]。
近些年來,關(guān)于樹枝形專用線取送車優(yōu)化方面,李斌等[2]以貨車總消耗時間最小化為優(yōu)化目標,同時提出遺傳蟻群算法求解該問題。溫旭紅等[3]提出了具有樹狀結(jié)構(gòu)的鐵路車流徑路優(yōu)化模型,設(shè)計拉格朗日松弛算法求解模型。郭垂江[4]以成本多目標為優(yōu)化模型,并設(shè)計模擬退火算法對模型進行求解。趙娟[5]以車流總走行車公里最小為目標,建立線性0-1規(guī)劃模型。張文晰等[6]針對路企直通列車組織過程中車流整列到發(fā)的取送問題,研究了裝卸區(qū)呈樹枝形布置成組裝卸情形的取送方案。郭垂江等[7]把取送車作業(yè)優(yōu)化問題轉(zhuǎn)換成哈密爾頓圖最短路問題,采用匈牙利算法進行求解。程磊等[8]以調(diào)機總走行時間最小為優(yōu)化目標,提出了一種改進蟻群算法求解該問題。
針對多目標模型優(yōu)化問題,相關(guān)文獻研究主要利用智能算法進行求解。湯兆平等[9]針對多目標規(guī)劃模型設(shè)計了基于TOPSIS方法和限定參數(shù)區(qū)間搜索的模型求解方法。陳希瓊等[10]構(gòu)建了最小化總行駛距離和最小化不同車輛行駛距離最大差以平衡各車輛的工作負荷的雙目標模型,并提出一種多目標蟻群算法。Aringhieri等[11]提出了基于鄰域搜索的啟發(fā)式算法解決多目標問題。葛顯龍等[12]設(shè)計了結(jié)合聚類分析和掃描算法的混合遺傳算法解決帶時間窗的路徑優(yōu)化問題。Mirakhorli等[13]設(shè)計了多目標線性規(guī)劃方法解決物流網(wǎng)絡(luò)優(yōu)化問題。Adamo等[14]研究了帶時間窗約束的貨物取送徑路和速度優(yōu)化問題,構(gòu)建了問題模型并給出了分支定界求解算法。Haddad等[15]研究了貨物分批取送問題,并設(shè)計了一個局部搜索啟發(fā)式算法。
就目前查閱的文獻來看,關(guān)于樹枝形專用線取送車優(yōu)化方面主要集中在調(diào)機取送成本和周轉(zhuǎn)時間的單目標優(yōu)化,考慮多目標優(yōu)化的文獻較為欠缺,此外較多文獻沒有考慮時間窗要求。因此,基于以上文獻研究,本文圍繞服務(wù)鐵路樞紐地方貨物流的小運轉(zhuǎn)作業(yè)系統(tǒng),研究一類帶時間窗的樹枝形專用線取送車優(yōu)化問題(optimization of placing-in and taking-out wagons on branch-shaped siding with time window,OPTWBS-TW),組建基于調(diào)運成本最小與貨車總周轉(zhuǎn)時間最小的雙目標數(shù)學規(guī)劃模型,提出了遺傳算法和模擬退火算法(genetic algorithm & simulated annealing, GA&SA)融合求解策略,最后進行實驗驗證與數(shù)值分析。
1 問題描述與研究條件
1.1 問題描述
本文所研究的OPTWBS-TW問題可以描述為:在鐵路樞紐樹枝形網(wǎng)絡(luò)N={i|i=0,1,…,A} 中,其中i=0 時表示編組站,i≠0時表示裝卸站,非直達列車陸續(xù)到達編組站,樞紐內(nèi)編組站對到達列車解體和出發(fā)列車編組,完成“列流轉(zhuǎn)變?yōu)檐嚵鳌焙汀败嚵鬓D(zhuǎn)變?yōu)榱辛鳌保b卸站對貨物進行裝車和卸車工作,完成“貨流轉(zhuǎn)變?yōu)檐嚵鳌焙汀败嚵鬓D(zhuǎn)變?yōu)樨浟鳌薄?紤]各裝卸站i的作業(yè)要求和時間窗限制,一臺調(diào)機往返編組站和裝卸站之間對所有作業(yè)進行取送工作。本文基于既考慮取送作業(yè)成本又考慮加速貨車周轉(zhuǎn),建立了調(diào)運成本最小和周轉(zhuǎn)時間最小的雙目標數(shù)學模型,其中調(diào)運成本分為調(diào)機走行成本、貨車走行成本和調(diào)機早到或晚到成本;周轉(zhuǎn)時間為調(diào)機將階段時間內(nèi)所有貨車從編組站送往裝卸站至作業(yè)完成后取回編組站的總完成時間。
1.2 研究條件
針對OPTWBS-TW問題,考慮如下研究條件:
(1)單調(diào)機作業(yè),調(diào)機最大牽引定數(shù)和最大走行時間已知;
(2)樹枝形專用線網(wǎng)絡(luò)中編組站、裝卸站間的機車走行時間已知;
(3)裝卸站待送貨車、待取貨車已知;
(4)裝卸站作業(yè)時間窗要求已知,即特定裝卸站有固定作業(yè)時間窗,調(diào)機在規(guī)定時間外到達裝卸站,會因裝卸站設(shè)備占用、整備等原因產(chǎn)生調(diào)機早到等待成本和調(diào)機晚到懲罰成本,即額外成本。
(5)調(diào)機在固定作業(yè)時間窗之前到達裝卸站,則調(diào)機等待至作業(yè)時間開始;調(diào)機在固定作業(yè)時間窗之后到達裝卸站,則直接開始工作。
(6)隨同一列車到達編組站,且目的裝卸站一致的貨車編為同一車組。車組取、送兩種作業(yè)獨立核算。
(7)不考慮貨車取送編組站后連掛列車。
2 模型構(gòu)建
2.1 符號約定
為構(gòu)建模型,引入以下參數(shù)與變量:
(1)輸入?yún)⒘?/p>
N:鐵路樞紐內(nèi)裝卸站集合,記為N={i|i=0,1,…,A}, 其中i=0時表示編組站,i≠0時表示裝卸站,A為鐵路樞紐內(nèi)的裝卸站總數(shù)。
t(i,j):裝卸站i到裝卸站j的走行時間,其中i或j=0表示編組站到裝卸站的走行時間,i,j∈N。
cl:調(diào)機單位分鐘運營成本。
cw:貨車單位分鐘運營成本。
P:調(diào)機最大牽引定數(shù)。
D:調(diào)機最大行駛時間。
L:陸續(xù)到達鐵路樞紐的貨物列車序號集合,記為L={l|l=1,…,B}。 其中B為到達的貨物列車總數(shù)。
l(i):隨貨物列車L到達鐵路樞紐且目的裝卸站為i的本地作業(yè)車組,l∈L,i∈N。
Ml(i):車組l(i)的貨車編組數(shù),l∈L,i∈N。
Tl(i):本地作業(yè)車組l(i)在目的裝卸站i處完成裝卸作業(yè)所需的時間,l∈L,i∈N。
Z:作業(yè)性質(zhì)集合,記為Z={z|z=1,2}, 其中z=1表示送車作業(yè),z=2表示取車作業(yè)。
U:取送作業(yè)編號集合,記為U={u=l(i)z|i∈N,l∈L,z∈Z}。l(i)1表示將車組l(i)送往裝卸站i的送車作業(yè);l(i)2表示將車組l(i)由裝卸站i取回編組站的取車作業(yè)。
[ETi,LTi]:表示裝卸站i允許的作業(yè)時間窗。ETi和LTi分別為裝卸站的最早作業(yè)時刻和最晚作業(yè)時刻,l∈L,i∈N。
K:調(diào)機取送批次集合,記為K={k|k=1,…,R}, 其中R為取送批次總數(shù)。
(2)狀態(tài)變量
ol(i): 本地作業(yè)車組l(i)到達編組站后到解完成時刻,l∈L,i∈N。
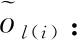
tl(i): 車組l(i)到達目的裝卸站i處送車時刻,l∈L,i∈N。

πk: 調(diào)機第k批次從編組站出發(fā)時刻,k∈K。

w(i,j): 調(diào)機從裝卸站i到裝卸站j所牽引的貨車數(shù)量,其中i或j=0表示編組站到裝卸站或裝卸站到編組站所牽引的貨車數(shù)量,i,j∈N。
αl(i): 裝卸站i的等待成本。調(diào)機在最早作業(yè)時刻ETi前到達裝卸站i,所產(chǎn)生的等待成本。記為αl(i)=e1(ETi-tl(i)), 其中e1為單位分鐘等待成本,i∈N。
βl(i): 裝卸站i的懲罰成本。調(diào)機在最晚作業(yè)時刻LTi后到達裝卸站i所產(chǎn)生的懲罰成本。記βl(i)=e2(tl(i)-LTi), 其中e2為單位分鐘懲罰成本,i∈N。
(3)決策變量
S(i,j): 0-1參數(shù),表示調(diào)機是否由裝卸站i駛向裝卸站j,如果調(diào)機途徑(i,j),則S(i,j)=1, 否則S(i,j)=0,其中i或j=0表示編組站,i,j∈N。
T:總周轉(zhuǎn)時間,即完成取送作業(yè)編號順序解ψ(l(i)z) 所需的總時間,i∈N,l∈L,z∈Z。
2.2 模型構(gòu)建
基于以上表述,以總調(diào)運成本最小化和貨車總周轉(zhuǎn)時間最小化為雙重目標,考慮時間窗要求,構(gòu)建問題模型。
(1)調(diào)運成本最小化目標,由3部分構(gòu)成,即調(diào)機走行成本、貨車走行成本和調(diào)機早到或晚到成本

(1)
(2)貨車總周轉(zhuǎn)時間最小化目標,以加速貨車周轉(zhuǎn)。貨車總周轉(zhuǎn)時間為調(diào)機將階段時間內(nèi)所有貨車從編組站送往裝卸站至作業(yè)完成后取回編組站的總完成時間
minZ2=T
(2)
(3)調(diào)機最大走行時間約束,即保證調(diào)機從編組站出發(fā)至回到編組站的走行時間小于調(diào)機的最大走行時間
(3)
(4)調(diào)機牽引定數(shù)約束,即調(diào)機牽引貨車數(shù)量不得超過調(diào)機牽引定數(shù)
w(i,j) (4) (5)取送作業(yè)順序約束,即同一車組作業(yè)先送后取,且送取作業(yè)的時間間隔大于貨物裝卸時間 第三,區(qū)域活動場地沒有得到完善。一些幼兒園為了節(jié)省成本投入,對幼兒活動場地建設(shè)以及器材的完善僅僅是流于形式。但是,在幼兒園區(qū)域活動中,活動器材以及場地都是非常重要的組成部分,直接影響到幼兒的身心發(fā)育。如果幼兒園在建設(shè)、布置的時候沒有考慮到幼兒的實際需求,那么這樣的區(qū)域活動條件則會嚴重影響區(qū)域活動開展有效性。 (5) (6)取送作業(yè)數(shù)目約束,即所有取車作業(yè)數(shù)目等于所有送車作業(yè)數(shù)目 (6) (7)變量取值約束 S(i,j)∈{0,1}, ?i,j∈N (7) (8)貨物作業(yè)時刻約束,即本地作業(yè)車組l(i)取回編組站完成時刻大于本地作業(yè)車組l(i)到達編組站后到解完成時刻 (8) 解決多目標優(yōu)化問題的最終目的只能是在各個目標之間進行協(xié)調(diào)權(quán)衡,使各子目標均盡可能達到最優(yōu)。本文采用理想最大值-最小值的雙目標歸一化處理,具體步驟如下: 步驟1 單目標下目標函數(shù)值的確定 通過計算機運行找到目標函數(shù)1的最小值Z1min、 最大值Z1max及目標函數(shù)2的最小值Z2min、最大值Z2max, 則目標函數(shù)1和目標函數(shù)2取值范圍分別為[Z1minZ1max]、 [Z2minZ2max]。 步驟2 目標函數(shù)值歸一化處理。 設(shè)第i條取送車徑路hi對應(yīng)的目標函數(shù)值1和目標函數(shù)值2分別為Z1i和Z2i,歸一化處理后目標函數(shù)值1和目標函數(shù)值2分別為Z1(hi)和Z2(hi),則 (9) (10) 該問題屬于NP-hard問題,利用傳統(tǒng)求解算法較為困難,且效率不高,故采用啟發(fā)式算法進行求解。考慮到遺傳算法GA能夠很好地解決優(yōu)化排序問題,且具備運行內(nèi)在隱蔽性和良好的穩(wěn)定性,故采用GA算法求解該問題,但GA算法容易陷入局部最優(yōu),且易早熟。模擬退火算法SA在解決優(yōu)化排序問題也有較好表現(xiàn),具有更好的全局收斂性,能夠很好互補GA算法的缺點,因此提出GA算法和SA算法融合求解該問題。該融合算法首先利用GA算法進入循環(huán)迭代,在每次迭代過程中,改進自適應(yīng)交叉變異概率以增強算法全局尋優(yōu)能力和收斂速度,最后利用SA算法進行二次迭代尋優(yōu),最終形成GA&SA融合求解算法。相對于遺傳算法、蟻群算法、粒子群算法等智能算法,GA&SA求解算法融合了GA和SA的優(yōu)點,同時嵌入?yún)?shù)自適應(yīng)調(diào)整策略,能更好地改善搜索的廣度和深度。GA&SA具體步驟如下。 根據(jù)鐵路樞紐內(nèi)裝卸站集合和陸續(xù)到達鐵路樞紐的貨物列車序號集合,其中裝卸站集合N={i|i=0,1,…,A}, 其中i=0時表示編組站,i≠0時表示裝卸站,A為鐵路樞紐內(nèi)的裝卸站總數(shù);貨物列車序號集合L={l|l=1,…,B}, 其中B為到達的貨物列車總數(shù),利用取送車徑路中的作業(yè)編號構(gòu)造問題的解,對于取送作業(yè)集合U,每個l(i)z表示一項取送車作業(yè),則所有取送車作業(yè)集合的排列組合即為取送車徑路的解,記為h,則取送車徑路的解表示為h={ψ(h(x))|h(x)=l(i)z,i∈N,l∈L,z∈Z,l(i)z∈U,x∈1,…,S}, 其中ψ(h(x)) 表示所有取送車作業(yè)集合的排列組合,S為取送作業(yè)編號集合數(shù)。設(shè)H=[h1,…,hw]T為初始取送車徑路種群規(guī)模,hw為一個取送車徑路的解,w為取送車徑路集合H中所涵蓋的取送車徑路數(shù)量。該編碼方式將一個時段內(nèi)的全部取送作業(yè)視為整體考慮,從而找出較優(yōu)取送車徑路。 4.2.1 選擇操作 令f1(hi)=θ*Z1(hi)、f2(hi)=(1-θ)*Z2(hi), 其中hi為一個取送車徑路的解。則適應(yīng)度函數(shù)f=1/(θ*f1(hi)+(1-θ)*f2(hi)), 那么每個取送車徑路個體被選擇的概率為Pi=f/∑f, 根據(jù)輪盤賭規(guī)則,隨機生成一個位于[0 1]的隨機數(shù)rand,并與隨機數(shù)rand進行比較從而確定選擇范圍。 4.2.2 交叉操作 為擴大解的搜索范圍,采用PBX交叉。具體過程如下: 步驟1 從上一代取送車徑路規(guī)模群體中隨機選擇一對父代取送車徑路個體h1和h2; 步驟2 選擇父代取送車徑路個體h1和h2若干個基因,位置可不連續(xù),但選擇一對父代取送車徑路個體的基因位置必須相同; 步驟4 找出被選中的基因在另一個父代取送車徑路個體的位置,在將其余基因按順序放入生成的子代取送車徑路個體中。具體過程如圖1所示,其中圖1(b)為生成的另一個取送車徑路。 圖1 PBX交叉過程 4.2.3 變異操作 設(shè)置兩點變異操作如下: 步驟1 從上一代取送車徑路規(guī)模群體中隨機選擇一個取送車徑路個體h3; 步驟2 對于取送車徑路個體h3,隨機產(chǎn)生兩個基因位τ1和τ2; 4.2.4 參數(shù)自適應(yīng)設(shè)計 針對GA參數(shù)的確定,設(shè)計動態(tài)交叉概率Pc和動態(tài)變異概率Pm, 使其隨實際環(huán)境的變化而不斷變化。當個體的適應(yīng)度較低時,增加交叉和變異的概率;反之,則降低交叉和變異的概率。具體設(shè)置如下 其中,fmax為種群中最大適應(yīng)度值;fave為種群平均適應(yīng)度值;f′為進行交叉的兩個父代染色體中較大的適應(yīng)度值;f為變異個體的適應(yīng)度值;Pcmax和Pcmin分別為交叉概率的上界與下界,設(shè)置 [pcmin,pcmax]=[0.5,0.99], [pmmin,pmmax]=[0.1,0.5],Q為迭代次數(shù),MQ為最大迭代數(shù)。 為進一步改善解的質(zhì)量,利用SA擴大搜索范圍,以找到更優(yōu)解。將迭代到一定次數(shù)后的GA算法導入SA進行二次尋優(yōu),對SA每個初始解和鄰域解進行評估,更新GA種群,循環(huán)往復(fù),直至滿足終止條件。 4.3.1 冷卻進度表的參數(shù)確定 冷卻進度表是控制SA算法進程的重要參數(shù),包括溫度控制參數(shù)T,初始溫度控制參數(shù)T0,溫度停止控制參數(shù)Tend,溫度衰減因子,馬爾科夫長度,初始馬爾科夫鏈長度0,馬爾科夫鏈變換因子δ,鄰域解變換次數(shù)q。 4.3.2 鄰域解的變換規(guī)則設(shè)計 4.3.3 鄰域解的接受概率設(shè)計 SA的二次尋優(yōu)更新過程具體步驟如下: 步驟1 基于GA初始取送車徑路生成。對迭代到一定次數(shù)的每代GA種群選擇最優(yōu)取送車徑路個體,記做hbest, 并計算Z1(hbest) 和Z2(hbest)。 步驟2 初始化參數(shù)。給定初始溫度控制參數(shù)T0,溫度停止控制參數(shù)Tend,溫度衰減因子,初始馬爾科夫鏈長度0,馬爾科夫鏈增加因子δ。令溫度控制參數(shù)T=T0,馬爾科夫長度=0, 初始鄰域解變換次數(shù)q=1。 步驟3 基于溫度控制參數(shù)衰減終止條件判斷。若T>Tend,則執(zhí)行步驟4,否則轉(zhuǎn)步驟7。 步驟5 鄰域解變換次數(shù)控制。令q=q+1, 若q<, 則執(zhí)步驟4進行鄰域解變換;否則步驟6。 步驟6 溫度控制參數(shù)T和馬爾科夫鏈長度更新。令T=T×,=×δ, 更新溫度控制參數(shù)T和馬爾科夫鏈長度。 步驟7 算法終止,輸出最優(yōu)取送車徑路hbest, 更新GA種群,從而進入下一代迭代尋優(yōu)。 設(shè)計由12個裝卸站組成的樹枝形小運轉(zhuǎn)作業(yè)網(wǎng)絡(luò),如圖2所示。設(shè)計實驗時段內(nèi)有4列貨物列車相繼到達編組站,各列車解體后的本地作業(yè)車取送信息數(shù)據(jù)見表1。樹枝形專用線網(wǎng)絡(luò)中各裝卸站及編組站間的調(diào)機走行時間數(shù)據(jù)見表2。 圖2 鐵路樞紐樹枝形專用線 表1 鐵路樞紐到達車流信息 表2 裝卸站間調(diào)機走行時間/min 根據(jù)以往文獻研究,對GA&SA算法的參數(shù)進行經(jīng)驗性設(shè)置:調(diào)機單位分鐘運營成本cl=16元,貨車單位分鐘運營成本cw=1.2元, 單位分鐘等待成本e1=2, 單位分鐘懲罰成本e2=8, 調(diào)機最大牽引定數(shù)P=40, 調(diào)機最大行駛時間D=300 min; 初始溫度控制參數(shù)T0=1000, 溫度停止控制參數(shù)Tend=0.01, 溫度衰減因子=0.9,初始馬爾科夫鏈長度0=2000, 馬爾科夫鏈變換因子δ=0.9, 初始鄰域解變換次數(shù)q=1, 最大迭代次數(shù)Q=160, 種群規(guī)模w=200。 當本文GA算法迭代到40代以后,利用SA算法進行二次尋優(yōu),得到GA&SA算法。 為了驗證算法的有效性,對所提出的GA&SA算法與本文所提的GA、SA以及蟻群算法(ant colony algorithm, ACA)進行性能對比測試,GA、SA算法參數(shù)與GA&SA算法保持一致,ACA參數(shù)設(shè)置參考文獻[8],利用Matlab R2014a對GA&SA、SA、GA和ACA求解策略進行編程,在Windows 8操作系統(tǒng),處理器為Intel(R) Core(TM) i5-3337U CPU(1.80 GHz) 微機上運行。對于雙目標函數(shù),本文θ分別取100%、50%、0%,從而輸出雙目標函數(shù)的求解質(zhì)量與算法迭代次數(shù)的演進關(guān)系如圖3所示,決策者可以根據(jù)實際需要,從中選擇較小的調(diào)運成本或者較小的貨車總周轉(zhuǎn)時間,或者二者折中。 圖3 不同θ值下求解質(zhì)量與算法迭代次數(shù)的演進關(guān)系 從圖3(a)可以看出:當θ=100%時,即決策者100%偏向目標函數(shù)1,隨著迭代次數(shù)的增加,4種算法總調(diào)運成本不斷下降,但總周轉(zhuǎn)時間呈現(xiàn)上升的趨勢。可以看出當決策者一味追求總調(diào)運成本最小時,求得的總周轉(zhuǎn)時間較長。 從圖3(b)可以看出:當θ=50%時,即決策者既考慮總調(diào)運成本,又考慮總周轉(zhuǎn)時間。隨著迭代次數(shù)的增加,4種算法目標函數(shù)值呈波浪式的下降。 從圖3(c)可以看出:當θ=0%時,即決策者100%偏向目標函數(shù)2,隨著迭代次數(shù)的增加,4種算法總周轉(zhuǎn)時間不斷下降,但總調(diào)運成本呈現(xiàn)上升的趨勢。可以看出當決策者一味追求總周轉(zhuǎn)時間最小時,求得的總調(diào)運成本較大。 總體來說:雙目標函數(shù)不存在絕對的最優(yōu)解,當決策者追求較低的總調(diào)運成本時,則總周轉(zhuǎn)時間則會較長;當決策者追求較短的總周轉(zhuǎn)時間時,則總調(diào)運成本則會較高。從運行結(jié)果可以看出GA&SA求解結(jié)果較好,SA求解結(jié)果較差。相對來說,SA、GA和ACA收斂較早,容易陷入局部最優(yōu),GA&SA收斂較晚,在迭代后期擴大了解的搜索范圍,得到更高質(zhì)量的解。故而,在嵌入?yún)?shù)自適應(yīng)GA中引入SA明顯提高了算法的性能。 為更直接觀察取送車取送作業(yè)情況,表3給出了在計算時間限定條件下的GA&SA、SA和GA算法計算結(jié)果,即將GA&SA的運行時間內(nèi)分別執(zhí)行GA和SA,以保證相同的運行時間,從而更公平的比較運行結(jié)果。設(shè)置θ=0.1, 其它參數(shù)不變。 從表3運行結(jié)果看出:GA&SA相對于GA和SA得到了更高質(zhì)量的解。GA&SA算法得到的最小周轉(zhuǎn)時間為720 min,總調(diào)運成本為43 099.8元;GA算法得到的最小周轉(zhuǎn)時間為736 min,總調(diào)運成本為45 600.8元;SA算法得到的最小周轉(zhuǎn)時間為812 min,總調(diào)運成本為54 890.4元,由此可以說明GA&SA相對于SA和GA改善了解的質(zhì)量。 表3 計算時間限定條件下的GA&SA、GA和SA算法計算結(jié)果 表3(續(xù)) 對于GA&SA運行結(jié)果,調(diào)機被劃分為7個批次,第1、2批次為同送模式,第3、4、5、6批次為取送結(jié)合模式,第7批次為同取模式;對于GA運行結(jié)果,調(diào)機被劃分為7個批次,第2、3批次為同送模式,第1、4、6批次為取送結(jié)合模式,第5、7批次為同取模式;對于SA運行結(jié)果,調(diào)機被劃分為8個批次,第1、2、4批次為同送模式,第3、7批次為取送結(jié)合模式,第5、6、8批次為同取模式。 本文圍繞鐵路樞紐地方貨物流,研究一類帶時間窗的樹枝形專用線取送車優(yōu)化問題,組建了基于調(diào)運成本最小與貨車總周轉(zhuǎn)時間最小的雙目標數(shù)學規(guī)劃模型,該模型通用性強,決策者可根據(jù)問題的具體情況選擇各種合理的取送作業(yè)方式。鑒于雙目標模型復(fù)雜,首先對雙目標模型進行基于理想最大值-最小值的歸一化處理,緊接著設(shè)計了GA&SA融合求解策略。該融合求解策略首先給出基于作業(yè)編號的取送車方案表述,進而設(shè)計嵌入?yún)?shù)自適應(yīng)策略的GA解更新過程,并設(shè)置SA算法進行二次尋優(yōu),從而找到最優(yōu)取送車徑路。最后設(shè)計仿真實驗,對所提出的方法進行過程驗證,結(jié)果表明,相對于GA、SA及ACA,融合求解策略GA&SA在解的質(zhì)量方面表現(xiàn)更佳。3 基于理想最大值-最小值的雙目標歸一化處理
4 基于雙目標的GA&SA混合算法
4.1 基于作業(yè)編號的取送車方案表述
4.2 嵌入?yún)?shù)自適應(yīng)策略的GA解更新過程


4.3 基于SA的二次尋優(yōu)更新過程


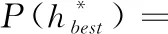
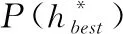



5 實驗驗證及結(jié)果分析
5.1 實驗場景

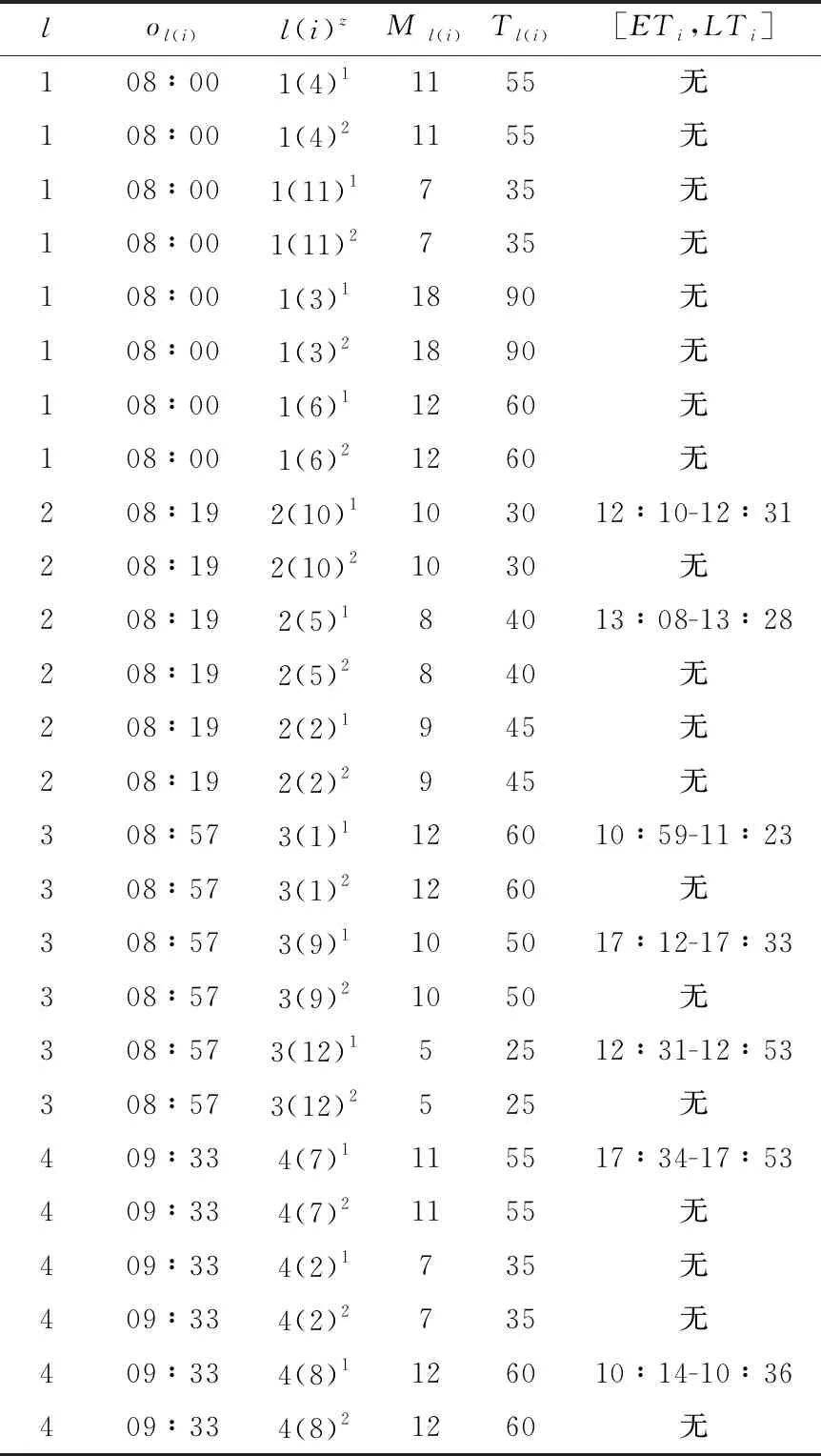

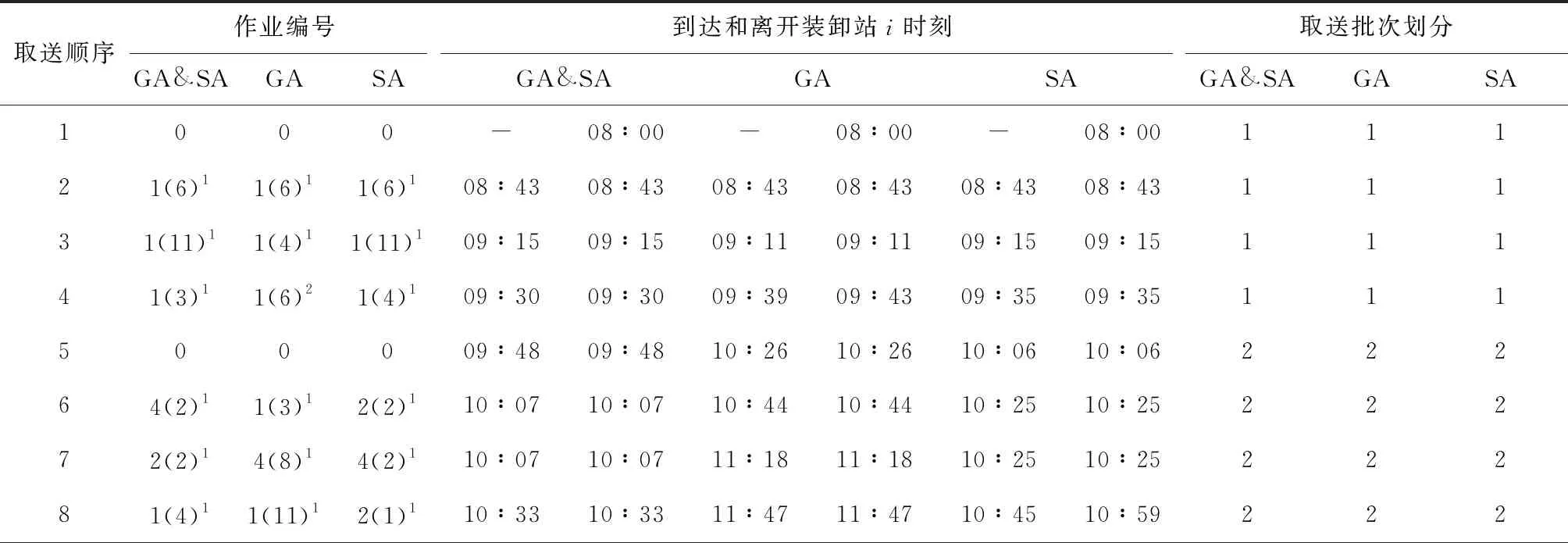
5.2 過程驗證


6 結(jié)束語

