基于風險指數的CTCS-3級列控系統設備剩余壽命預測
王瑞峰,姚軍娟
(蘭州交通大學 自動化與電氣工程學院,甘肅 蘭州 730070)
列控系統作為鐵路信號的核心部分,對其設備的剩余壽命進行預測,可提前制定相應的維修及備件策略,保證行車安全。
近年來,對于列控系統設備的研究主要集中在可靠性、故障診斷和維修等方面。文獻[1]從可靠性的角度,分析了車載設備在不同故障情況下的彈復能力,并提出相應維修策略。文獻[2]從可靠性及可用性的角度,對列控中心進行了評估,找出系統薄弱環節以提高維護管理水平。文獻[3]從故障識別的角度,對列控車載設備進行了故障診斷和分類。文獻[4]從時變可靠度的角度,確定列控系統的維修周期。不難看出,基于可靠性和故障診斷的列控系統設備的維修還存在一定的局限性。然而在航天和航空領域,對設備狀態評估和剩余壽命預測方面進行了大量研究[5-7]。而在鐵路領域,對列控系統設備的狀態評估和剩余壽命預測方面的研究相對較少。
本文建立了基于風險指數的CTCS-3級列控系統設備剩余壽命預測模型,包括基于模糊層次分析法和實驗室決策法(AHP-DEMATEL)的風險指數模型和基于不確定理論的剩余壽命預測模型。通過對CTCS-3級列控系統設備風險狀態的評估,建立了設備風險狀態隨運行時間變化的規律,并在此基礎上,實現對設備壽命及剩余壽命的預測。
1 CTCS-3級列控系統設備風險指數模型
1.1 設備風險狀態等級劃分
基于文獻[8]中描述的鐵路信號設備狀態信息,將CTCS-3級列控系統設備風險狀態量化,采用風險指數(Risk Index,RI)來描述設備的風險狀態。規定RI的取值范圍為0~100。CTCS-3級列控系統設備風險狀態等級劃分見表1。
1.2 構建設備風險指數模型
影響CTCS-3級列控系統設備安全的因素眾多,對設備狀態的影響具有模糊性和隨機性,因此采用基于模糊AHP-DEMATEL法的風險指數模型。
1.2.1 確定指標體系
綜合考慮影響CTCS-3級列控系統設備安全的因素,以歷史工況、基本狀況和運行工況3個方面建立其風險狀態評估指標體系,見圖1。其中:歷史工況包括檢修質量和故障頻率,反映了設備當前的實際狀態;基本狀況包括性能參數和產品質量史,反映了設備安全運行相關的理想狀態;運行工況包括運行狀態、運行環境和運行時間,反映了設備運行相關的實時狀態。圖1中,U層為目標層,A層為主準則層,B層為次準則層。

表1 CTCS-3級列控系統風險狀態等級
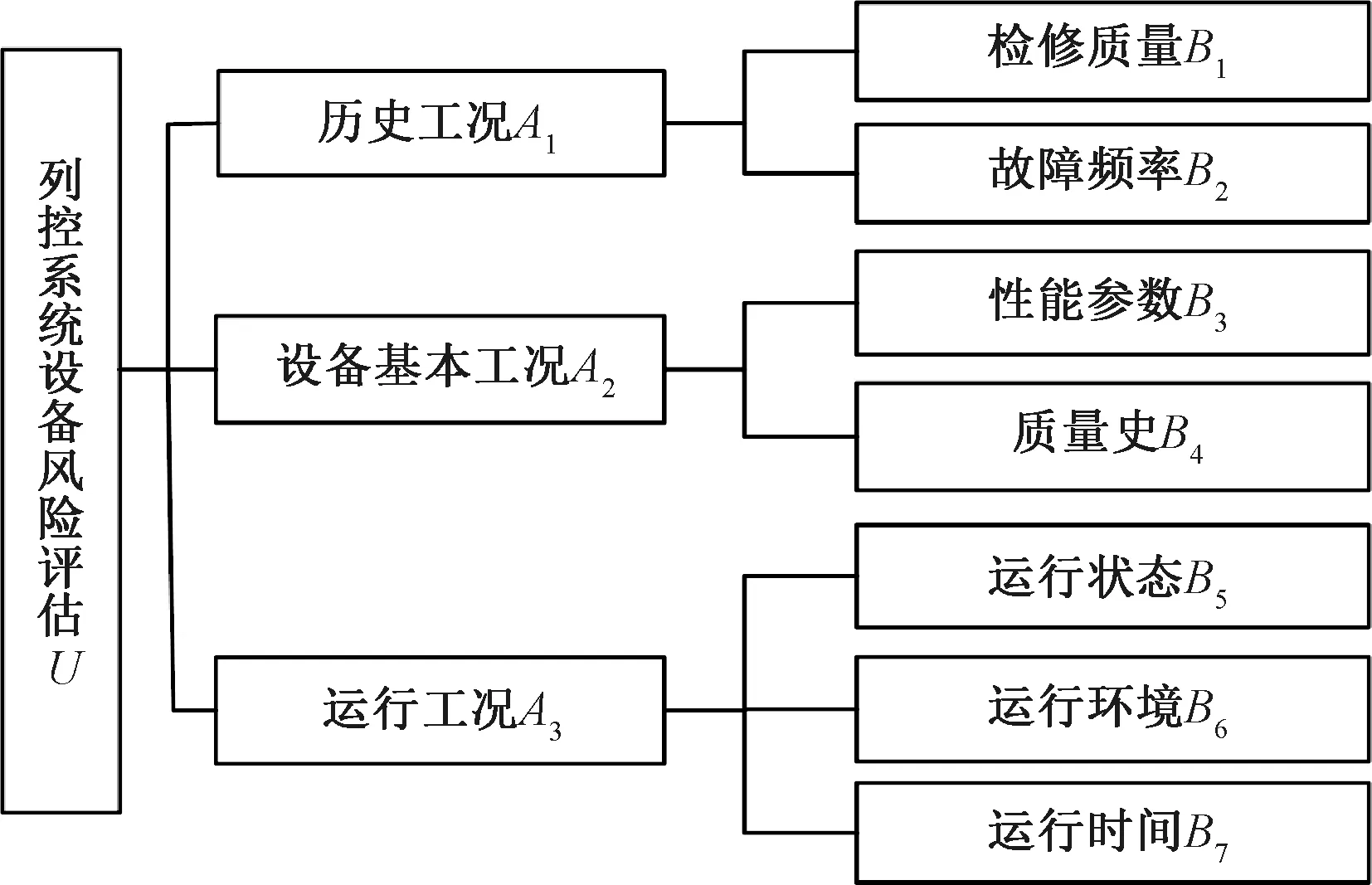
圖1 風險狀態評估指標體系
1.2.2 計算指標綜合權重
采用AHP-DEMATEL法確定各指標綜合權重zi。由于AHP法[9]未考慮因素之間的相互影響關系,而CTCS-3級列控系統設備風險因素涉及面較廣,很難保證各因素的獨立性,故引入DEMATEL法[10],綜合考慮各指標之間影響程度,以克服專家主觀性。具體計算流程如下:
(1)采用AHP法計算指標初始權重。
(2)采用DEMATEL法計算指標中心度。
(3)計算指標綜合權重,即指標初始權重與中心度之積。
1.2.3 設備風險狀態評估
采用模糊綜合評價法對CTCS-3級列控系統設備進行風險狀態評估,評估結果即為風險指數RI。具體計算過程如下:
Step1確定隸屬度矩陣R
R=(rij)i×4。rij為評估集U中第i指標對評價集V(風險低Ⅰ、風險較低Ⅱ、風險較高Ⅲ、風險高Ⅳ)中第j(j=1,2,3,4)個元素的隸屬度。隸屬度rij=mij/M,M為專家總人數,mij表示有m個專家對第i指標的評語為Vj。
Step2確定模糊綜合評判矩陣B
CTCS-3級列控系統設備風險狀態評估的模糊綜合評判矩陣為
(1)
Step3確定風險狀態評估結果RI
采用模糊向量單值化法求CTCS-3級列控系統設備風險指數為
RI=B·C
(2)
式中:C為CTCS-3級列控系統設備風險狀態評估等級分值,它與風險狀態評估等級之間的關系見表2。

表2 風險狀態評估等級與等級分值對照
2 CTCS-3級列控系統設備剩余壽命預測模型
2.1 建立風險指數RI的隨機模糊分布函數和曲線圖
CTCS-3級列控系統設備,隨著運行時間的增加,設備的退化水平不斷增大,從而導致設備失效的風險也越大。由于組成列控系統的各功能模塊失效分布一般服從指數分布[11],因此建立基于指數分布的CTCS-3級列控系統設備風險指數的分布函數為
RI(t)=a0+beλt
(3)
式中:a0、b和λ為常數。
根據文獻[12]描繪的列控系統風險曲線圖,以及式(3)建立的風險指數分布函數,建立CTCS-3級列控系統設備風險指數曲線,見圖2。

圖2 CTCS-3級列控系統設備風險指數曲線
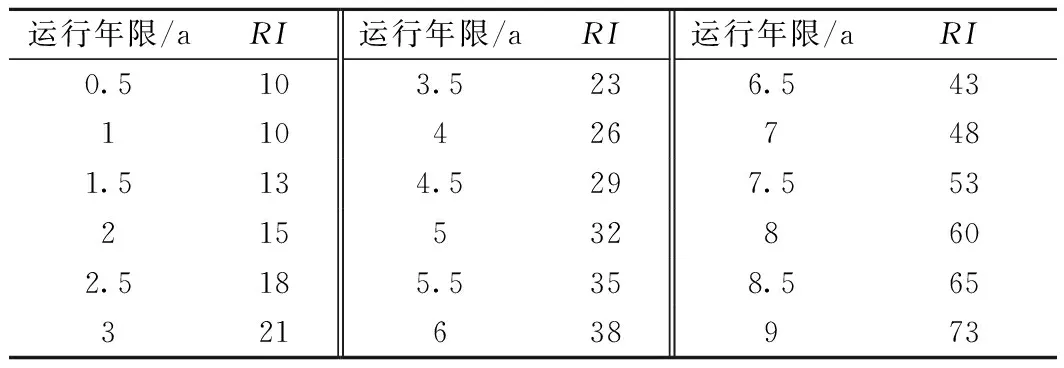
由圖2可知,CTCS-3級列控系統設備風險指數隨運行時間t呈指數規律上升。當RI≤60時,設備處于正常狀態,風險較小;當60 采用三角模糊變量an=(a0,a1,a2)將風險指數分布函數中的參數a0模糊化,建立CTCS-3級列控系統設備風險指數RI的隨機模糊分布函數為 RI(t)=an+beλtan=(a0,a1,a2) (4) 式中:t為CTCS-3級列控系統設備運行年數。 根據上述CTCS-3級列控系統設備的風險指數對其剩余壽命進行預測。CTCS-3級列控系統設備的壽命是指設備在失效之前的最大運行時間,即 T=max{t|RI(t)≤RImax} (5) 式中:RImax為CTCS-3級列控系統設備所允許的最大風險指數;T為設備的壽命。 由圖2知,b>0,λ>0,將式(4)代入式(5)可推導出CTCS-3級列控系統設備的運行時間t滿足 (6) 由此,基于不確定性理論[13-15],建立CTCS-3級列控系統設備最大機會約束下剩余壽命預測模型為 (7) 式中:α、β為置信水平;Tr為CTCS-3級列控系統設備剩余壽命。 由于CTCS-3級列控系統設備剩余壽命預測模型包含不確定函數,很難用傳統方法求解,因此采用隨機模糊模擬技術求解上述建立的模型。具體實現步驟如下: Step2假設μn=(2Mcr{an})∩1。其中:μn為模糊變量an的隸屬度;n=1,2,…,N;N為隨機模糊模擬次數。 Step3對于每個模糊變量an,采用隨機模糊模擬技術求出滿足Cr{f(an)≥r}≥β的期望目標可信度,求解公式為 (8) 式中:f(an)為模糊變量an的可測函數;r為任意實數。 Step4求解滿足L(r)≥α時的r的最大值rmax。rmax即為CTCS-3級列控系統設備的壽命T,用T減去設備已運行年限t,最終得到設備的剩余壽命Tr。 CTCS-3級列控系統設備剩余壽命預測模型求解流程見圖3。 圖3 剩余壽命預測模型求解流程 列車超速防護系統(ATP)是列車運行控制系統的核心,具有保證列車安全運行的重要功能。車載ATP主機作為ATP系統的重要組成部分,主要功能是生成速度監控曲線,以防列車超速行駛[16]。鑒于車載ATP主機在保障行車安全方面的重要作用,結合上述CTCS-3級列控系統風險指數模型和剩余壽命預測模型,對某鐵路局一臺運行9 a的CTCS-3級列控系統車載ATP主機進行剩余壽命預測。 3.1.1 采用AHP法計算初始權重 根據列控設備動態監測系統(DMS)對CTCS-3級列控系統設備狀態的實時監測數據和專家經驗,采用傳統1~9標度法構造車載ATP主機風險狀態評估指標的判斷矩陣。傳統1~9標度法見表3,構造的判斷矩陣見表4~表7。 表3 傳統1~9標度法 表4 判斷矩陣U -A 表5 判斷矩陣A1 -B 表6 判斷矩陣A2 -B 表7 判斷矩陣A3 -B (1)由表4~表7求得車載ATP主機風險狀態評估指標的初始權重為 wU=(0.154,0.641,0.206) wA1=(0.889,0.111) wA2=(0.875,0.125) wA3=(0.068,0.685,0.247) (2)為了驗證上述判斷矩陣的構建是否合理,需要對其進行一致性檢驗,檢驗公式為 (9) (10) 式中:CR為判斷矩陣隨機一致性比率,當CR<0.1,說明判斷矩陣滿足一致性要求,構建合理;CI為一致性檢驗標度;λmax為上述判斷矩陣的最大特征值;k為判斷矩陣的維數;RI為隨機一致性指標,見表8。 表8 隨機一致性指標 取RI=1.32,計算結果為 λmaxU=3.167,CIU=0.0835,CRU=0.063<0.1 λmaxA1=1.999,CIA1=-0.001,CRA1=-0.001 λmaxA2=2,CIA2=0,CRA2=0<0.1 λmaxA3=3.250,CIA3=0.125,CRA3=0.095<0.1 由此可知,上述判斷矩陣滿足一致性,其構建合理。 (3)車載ATP主機風險狀態評估B層各指標對U層總排序見表9。 表9 B層各指標對U層總排序 對總排序結果進行一致性檢驗,檢驗公式為 (11) 可得 0.019<0.1 根據計算結果可知,綜合排序滿足一致性檢驗,即車載ATP主機風險狀態評估各指標權重分配合理。 3.1.2 計算綜合權重 (1)直接影響矩陣 用0~3標度來表示車載ATP主機風險狀態評估各指標之間的影響強度,其中0、1、2、3分別對應“沒有影響”“有影響”“較大影響”“較強影響”。通過專家打分,確定不同指標間的影響程度,得出直接影響矩陣,見表10。 表10 直接影響矩陣 (2)規范化直接影響矩陣 對直接影響矩陣進行規范化處理,得到如表11所示的規范化直接影響矩陣,計算公式為 (12) (3)綜合影響矩陣 由式(13)求得綜合影響矩陣,結果見表12。 F=B(I-B)-1=(tij)7×7 (13) 表11 規范化直接影響矩陣 表12 綜合影響矩陣 (4)綜合權重 中心度hi綜合反映了各指標對車載ATP主機風險狀態評估的重要性,計算公式為 (14) (15) hi=fi+gi (16) 車載ATP主機風險狀態評估指標的綜合權重zi為 (17) 綜合權重計算結果見表13。 表13 綜合權重 通過計算風險低、風險較低、風險較高和風險高共4個評語集V內專家人數m與專家總人數M(M=10)的比例,構建了底層指標的隸屬度,從而得到車載ATP主機各指標的隸屬度矩陣,見表14。 表14 車載ATP主機各指標隸屬度 由式(1)得,車載ATP主機風險狀態評估向量為 B=(0.1328,0.2125,0.3619,0.2918) 根據式(2),車載ATP主機的風險指數為 RI=0.133×30+0.213×65+0.362×77.5+ 0.292×92.5=72.90 即該臺車載ATP主機的風險指數RI為72.9,約為73,其風險狀態處于Ⅲ級,風險較高,設備發生故障的可能性較大,需加強監測。采用同樣的方法,得到車載ATP主機歷年的風險指數,見表15。 表15 車載ATP主機歷年的風險指數 采用Matlab擬合出車載ATP主機的風險指數曲線,見圖4,風險指數的分布函數為 RI(t)=-8.237+16.57e0.175 6t (18) 圖4 車載ATP主機的風險指數曲線 由于CTCS-3級列控系統設備風險指數的分布函數RI(t)是關于參數an的模糊隨機分布,則車載ATP主機風險指數的模糊隨機分布函數為 RI(t)=an+16.57e0.175 6t (19) 將車載ATP主機的風險指數分布函數式(19)代入式(7)得 當β=RImax=92.5,α=0.95時,取an=(-10.132,-8.237 ,-6.215 ),采用隨機模糊模擬技術求解式(20),得車載ATP主機的壽命為T=10.28 a,則其剩余壽命為Tr=10.28-9=1.28 a。 (1)本文建立了基于模糊AHP-DEMATEL法的CTCS-3級列控系統設備風險指數模型。該模型能夠較準確地反映當前設備風險狀態水平的高低。 (2)以風險指數為基礎,建立了基于不確定理論的CTCS-3級列控系統設備剩余壽命預測模型。該模型不僅反映了CTCS-3級列控系統設備風險狀態隨運行時間的變化規律,實現對設備風險狀態的實時追蹤,還較準確地預測了設備壽命以及剩余壽命。本文以一臺運行了9年的車載ATP主機為例,驗證了該方法的可行性,符合車載ATP主機現場每十年更新的要求[17]。 (3)基于風險指數的CTCS-3級列控系統設備剩余壽命預測模型,可有效掌握設備的實時風險狀態,實現設備的優先修護以及節約維修成本。2.2 建立基于不確定理論的剩余壽命預測模型
2.3 求解設備剩余壽命預測模型
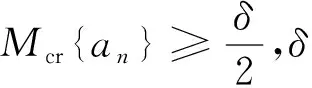
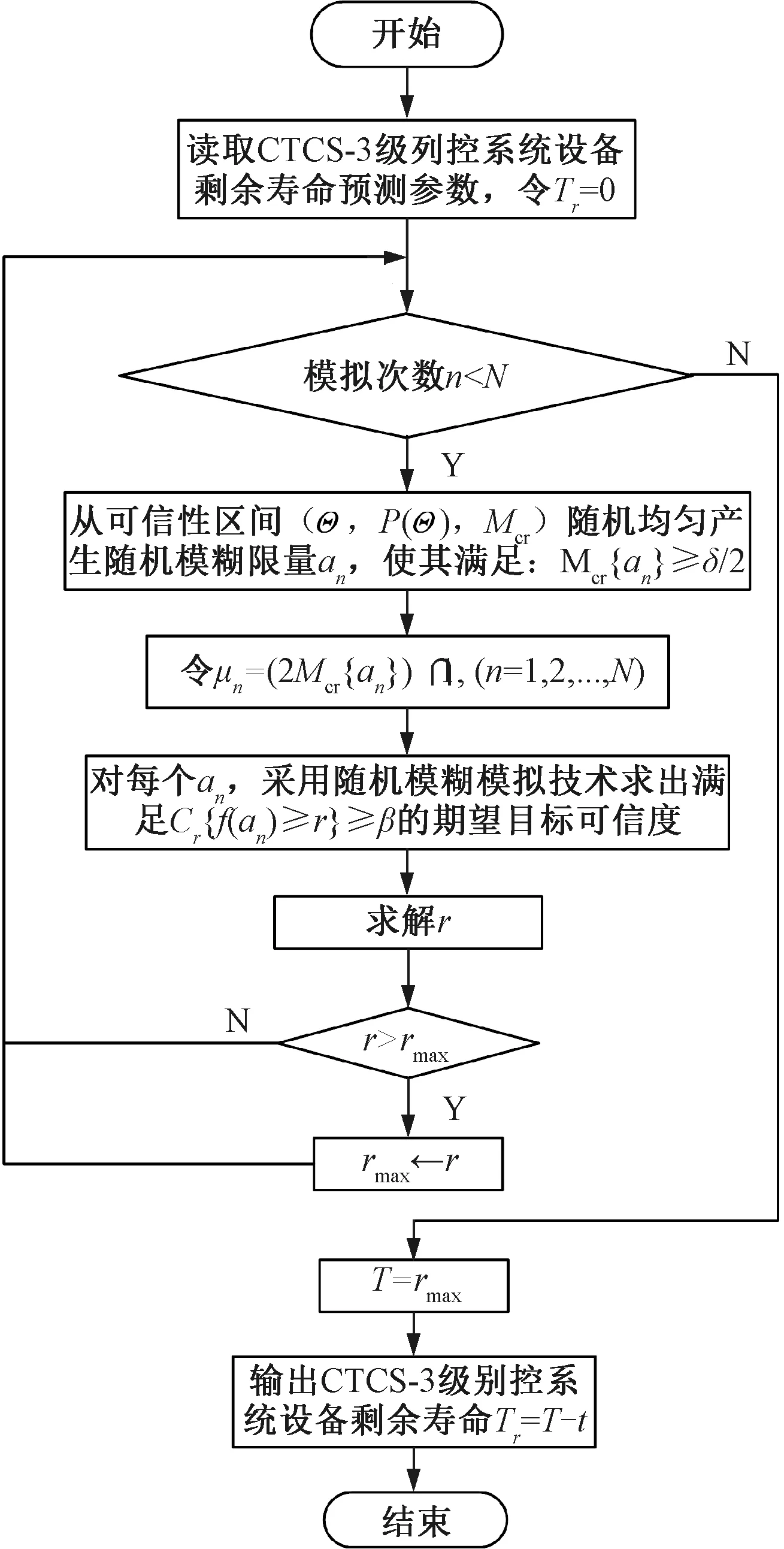
3 實例驗證及分析
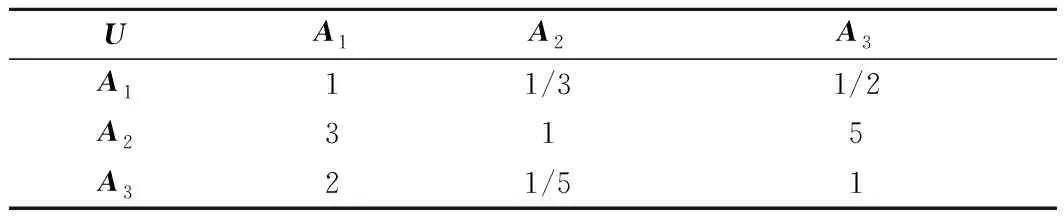
3.1 計算車載ATP主機的風險狀態指標綜合權重



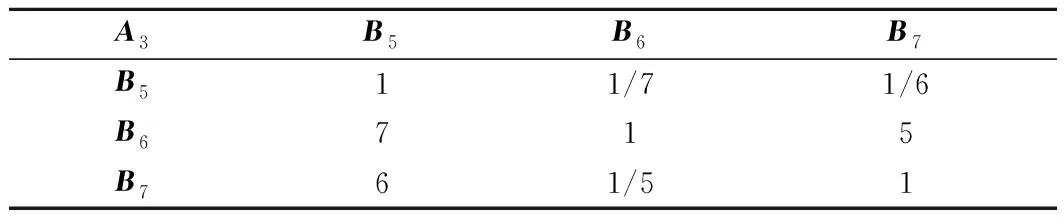

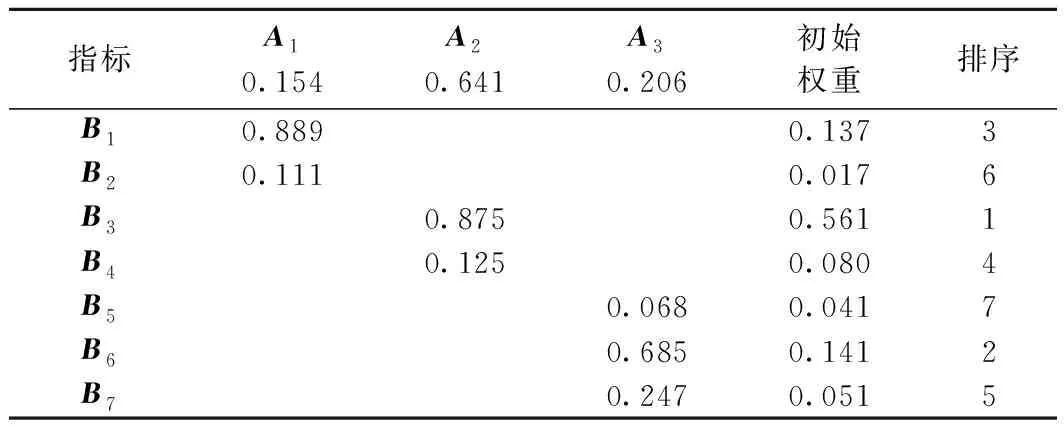
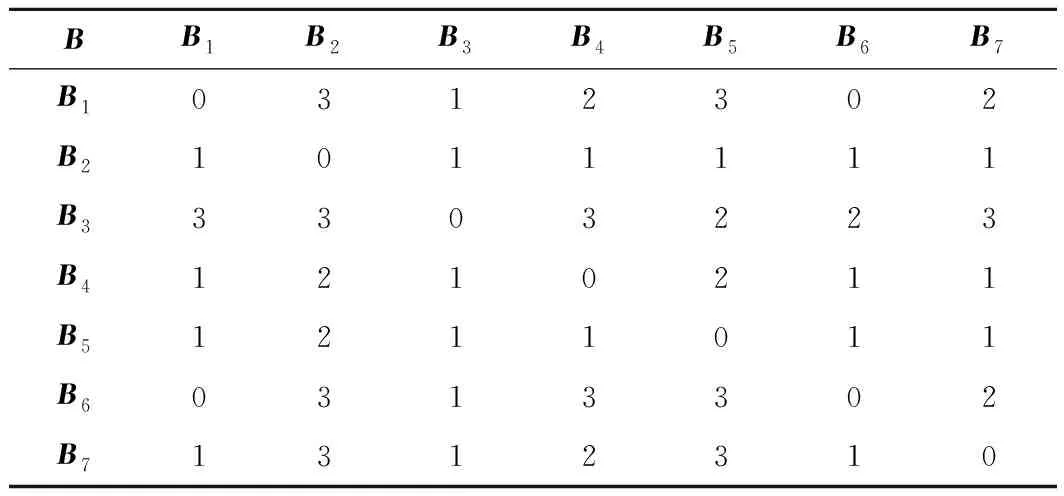



3.2 確定車載ATP主機的風險指數
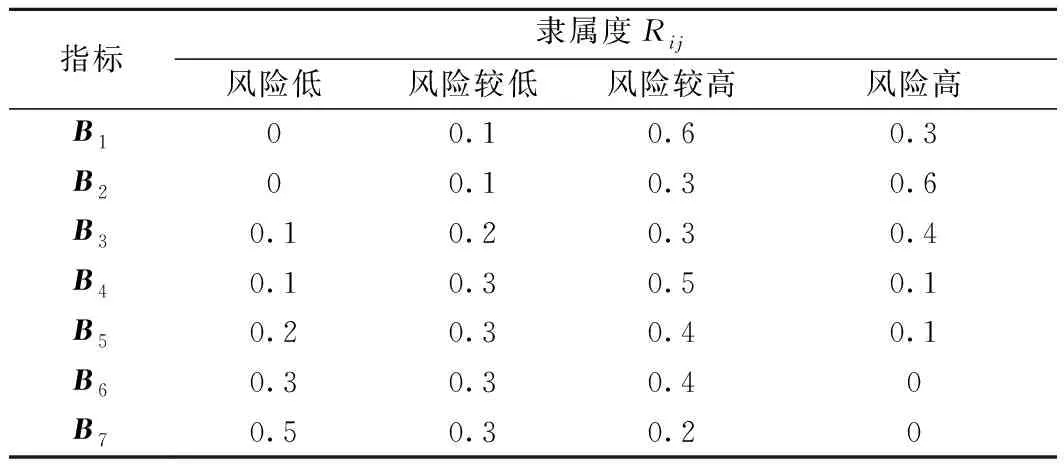

3.3 預測車載ATP主機的壽命和剩余壽命
4 結論

