最小最大二點集覆蓋問題分析及改進算法設計

徐 弈， 陳 瑩

（1.西安理工大學 經濟與管理學院，陜西 西安710054；2.西安交通大學 管理學院，陜西 西安710049）

0 引言

近些年，選址問題中的二中心問題及其擴展問題已成為主要的研究方向之一，其中平面點集的二中心問題更是人們關注的重點問題，該問題定義如下：給定平面點集P，求兩個圓的并覆蓋整個點集，使得兩個圓半徑的最大值最小。Drezner在1984年首次給出了O（n3）時間復雜性的算法［1］。1994年，Agarwal和Sharir兩人給出了第一個接近平方級別的算法—O（n2log3n）的確定時間算法［2］，而該算法的中心思想來源于Hershberger和Suri兩人于1991年給出的二中心問題的判定問題解法［3］。所謂判定問題，即為給定半徑r＞0，問是否存在兩個半徑為r的全等圓覆蓋P。他們給出這個判定問題可以在O（nlogn）的時間內求解。緊接著在1994年，Jaromczyk和Kowaluk給出了O（n2logn）時間復雜性的算法［4］。作為一個突破，通過結合之前Hershberger和Suri提出的判定問題解法，1997年Sharir利用參數搜索技巧設計并行算法，將求解二中心問題的時間復雜性降到了O（nlog9n）［5］，這是歷史上第一個接近線性時間的確定算法。同年，同樣運用參數搜索設計并行算法，Eppstein給出了O（nlog2n）的期望時間算法［6］。1999年，Chan對Sharir給出的算法又做了進一步改進，給出了到目前為止最快的算法，其時間復雜性為O（nlog2nlog2logn）［7］。對離散二中心問題，即限定兩個圓的圓心在點集P內，Hershberger和Suri在他們求解判定問題的文章中給出離散二中心問題可以在O（n2logn）時間內求解［3］。通過運用Katz和Sharir提出的幾何優化問題中的擴展方法，Agarwal和Sharir等人給出目前為止最快的算法，其時間復雜性為O（n4/3log5n）［8］。而二中心問題的在線情況，由Zhu等人于2013年提出并給出近似比為5.611的近似算法［9］，接著該問題在2015年被Kim等人將近似比改進到1.865［10］。

本文著重討論二中心問題的一個擴展問題-最小最大二點集覆蓋問題，并對該問題已有算法進行改進。2003年，Huang等人考慮了α連通二中心問題［11］。他們首先考慮這個問題的判定問題，即：給定半徑r＞0，是否存在兩個半徑為r的全等圓，使兩圓的并覆蓋P并且圓心距與半徑之比小于常數α。通過最遠點Voronoi圖與點集中心包的關系，他們給出這個問題的判定問題可以在O（n2log2n）的時間內求解。接著在2006年，通過運用參數搜索設計并行算法，他們給出α連通二中心問題可以在O（n2log2n）的期望時間內求解［12］。2019年，Xu等人考慮這個問題的衍生問題，即圓心限制在點集內部的混合與離散情況，對這兩種情況他們分別給出復雜性為O（n2log2n）和O（n2logn）時間的確定算法［13］。2014年，Kavand提出了（n，1，1，α）中心問題，即求解兩個圓使其分別覆蓋點集P，滿足其圓心距不小于α且大圓的半徑最小［14］。通過運用最遠點Voronoi圖［15～17］，他們證明該問題最優解的兩個圓一定全等，并且給出O（nlogn）時間復雜性的算法。本文所考慮的最小最大二點集覆蓋問題也可以看成是二中心問題的擴展問題，問題的描述如下：

問題1給定兩個平面點集P1和P2，分別包含m和n個點，求兩個圓分別覆蓋P1和P2，滿足兩個圓的半徑與圓心距三者中的最大值最小。

對該問題，2006年Huang等人通過運用參數搜索設計并行算法給出這個問題可以在O（（m+n）log（m+n））的確定時間內求解［9］。但是注意到，他們所設計的并行算法，需要處理器的個數為O（m+n），而當m和n足夠大時，這是不可能實現的。為了改進這個缺陷，本文同樣給出接近線性時間的確定時間算法，但是與之不同的是本文提出的算法不需要運用并行計算，從而大大提高了算法的可實現性.本文結構如下：第1節回顧點集的最遠點Voronoi圖與點集中心包的關系；第2節給出最小最大二點集覆蓋問題的最優解幾何結構；第3節重點研究在同一個半徑變化過程中，兩個點集中心包之間的最近距離變化關系；第4節通過該變化關系設計最小最大二點集覆蓋問題算法；第5節給出結論與展望。

1 最遠點Voronoi圖與點集中心包關系

在討論最小最大二點集覆蓋問題之前，先給出本文所用到的一些符號：記P1和P2為平面上分別包含m和n個點的點集，D（o，r）為以o為圓心，r為半徑的圓盤，C（o，r）為圓盤D（o，r）的邊界（即圓圈），稱C（o，r）上的點為控制點。對任意兩點｛x，y｝，記d（x，y）為兩點之間的歐氏距離，lx，y為過兩點的線段。在討論設計算法之前，首先介紹一個點集的中心包與最遠點Voronoi圖之間的關系［11］。對任意點集P，其對應以r為半徑的中心包定義如下［3，11］：

定義1對點集P而言，其以r為半徑的中心包CHr（P），是以P中的所有點為圓心，r為半徑的圓盤的交，即CHr（P）∩p∈PD（p，r）。

對點集P的中心包，有以下幾個關鍵性質［11］。

性質1記點集P的最小覆蓋圓半徑為r0，則CHr（P）＝?當且僅當r＜r0。

性質2點p在CHr（P）內當且僅當p到P中的最遠點距離小于等于r。

由性質2與最遠點Voronoi圖的定義，又得到如下性質：

性質3CHr（P）上的每個弧在所對應圓心的最遠點Voronoi區域內。

由性質1、性質2和性質3可以得到以下關鍵性質：

性質4點集P的中心包CHr（P）弧的個數隨半徑r的變化如下：隨著半徑的增加，每當半徑超過P的最遠點Voronoi圖的一個交點到其對應最遠點之間的距離，則中心包弧的個數增加1。

2 最優解幾何結構與性質

記P1和P2的最小覆蓋圓分別為D（o1，r1）和D（o2，r2）（不失一般性，假設r1≥r2），同時令最小最大二點集覆蓋問題最優解所對應P1和P2的覆蓋圓分別為D（）和D（），由問題1可以得到其等價形式：

問題2最小最大二點集覆蓋問題等價于兩個全等的圓分別覆蓋P1和P2，并且要求半徑與圓心距二者中的最大值最小。

本文著重通過點集中心包的性質來研究問題2。由問題2可以看出，此時最優解結構存在兩種情況：

情況1圓心距小于等于圓半徑。

由于兩個點集P1，P2已經給定，因此可以通過計算這兩個點集各自的最小覆蓋圓進行檢測。如果滿足d（o1，o2）≤r1，則此時已然得到最優解；否則，計算點集P2在r1下的中心包CHr1（P2），如果滿足o1到CHr1（P2）的最短距離小于等于r1，則此時仍然得到最優解，這里取該最近點為覆蓋P2的圓所對應的圓心，r1為覆蓋半徑即可。

情況2圓心距大于圓半徑。

對這種情況，最優解半徑一定大于max｛r1，r2｝。從直觀角度看，這時需要同時增加兩個點集各自覆蓋圓的半徑，并且同時將兩個圓的圓心相互靠攏，直到兩圓圓心距與半徑相同時得到最優解。此時，最優解情況可以分為以下三種：

情況2a最優解由兩個控制點決定。

情況2b只有一個圓有一個控制點。

情況2c兩個圓至少都有兩個控制點。針對情況2a，此時有：

引理1這兩個控制點和兩個圓心共線。

證明記這兩個控制點為a和b，其中a∈C（，r），b∈C（，r）。不失一般性，假設a與兩個圓心不共線，則一定在的鄰域Nε（）內存在一個新的圓心，使得D（，r）仍然能夠覆蓋P1。同時，在的鄰域Nε／2（）內也一定存在一個新的圓心，使得D，r-ε／10）能夠覆蓋P2并且滿足d（）＜r，注意到這時D（，r）和D（，r-ε／10）均不是點集P1和P2的最小覆蓋圓，這意味著一定存在兩個半徑更小，且兩圓圓心距小于r的圓分別覆蓋P1和P2，這與最優解假設相矛盾（見圖1）。

通過引理1，直觀地可以看出和一定分別在C（a，r）和C（b，r）上，又因為｛a，b｝為兩個圓的控制點，再由中心包定義，可以得到和一定分別在CHr（P1）和CHr（P2）的一條弧上。

圖1 引理1說明

針對情況2b，此時與情況2a類似的有：

引理2這個控制點與兩個圓心共線。

證明設b為圓D，r）的唯一控制點。若b不與兩個圓心共線，則與引理1類似的可以證明，一定存在兩個圓分別覆蓋P1和P2，并且滿足max｛r-ε／10，d（）｝＜r（見圖2）。

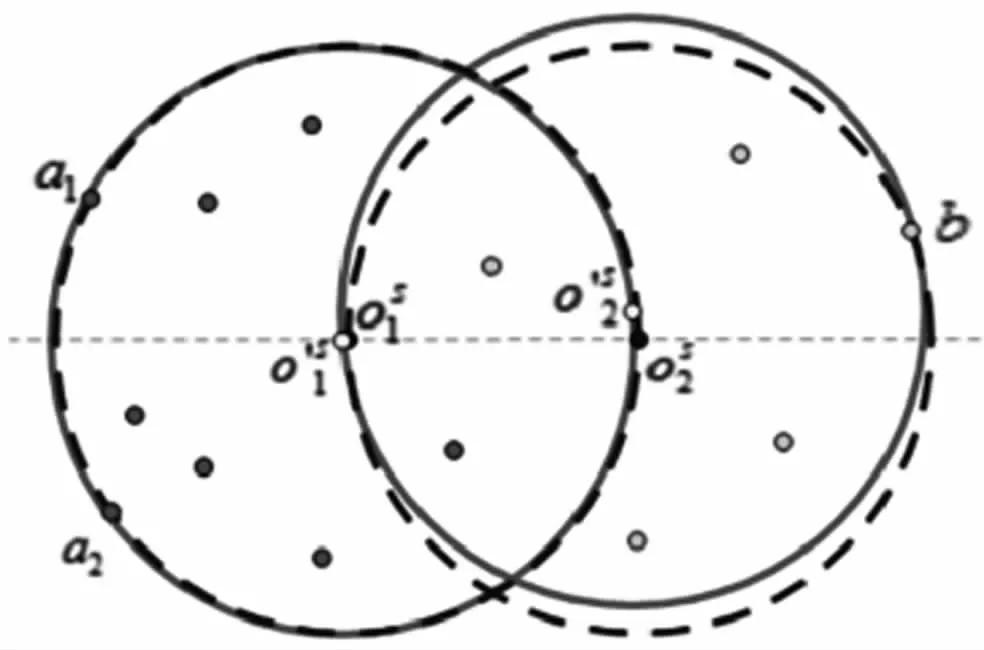
圖2 引理2說明

由引理2可知，記另一個圓的兩個控制點分別為a1和a2，有在C（a1，r）和C（a2，r）的交點上，在C（b，r）上，即有一定在CHr（P1）的一個頂點上，一定在CHr（P2）的一條弧上。

針對情況2c，這兩個圓都至少有兩個控制點。不失一般性，假設這兩個圓各自只有兩個控制點，按照逆時針方向，記為｛a1，a2｝和｛b1，b2｝，可以得到以下最優結構

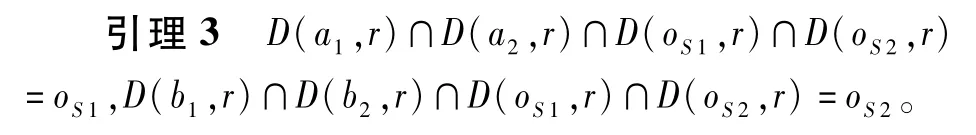
證明假設D（a1，r）∩D（a2，r）∩D（oS1，r）∩D（oS2，r）不止有oS1這一個點。則此時一定存在一個新的圓心，使得D（，r）能夠覆蓋P1∪滿足此時的情況有兩種：（1）｛a1，a2｝分布在過兩圓心的直線lo S1，o S2的同側（見圖3（a））；（2）∠＞180°（以逆時針方向，見圖3（b））。此時，與引理1，引理2證明類似，一定存在兩個半徑更小，且圓心距小于r的圓覆蓋P1和P2。同理可證D（a1，r）∩D（b2，r）∩D（oS1，r）∩D（oS2，r）＝

這時，在C（a1，r）和C（a2，r）的交點上在C（b1，r）和C（b2，r）的交點上，由｛a1，a2｝和｛b1，b2｝分別為兩圓的控制點，有和分別在CHr（P1）和CHr（P2）的一個頂點上。下一節將重點對這種結構給出相關分析。

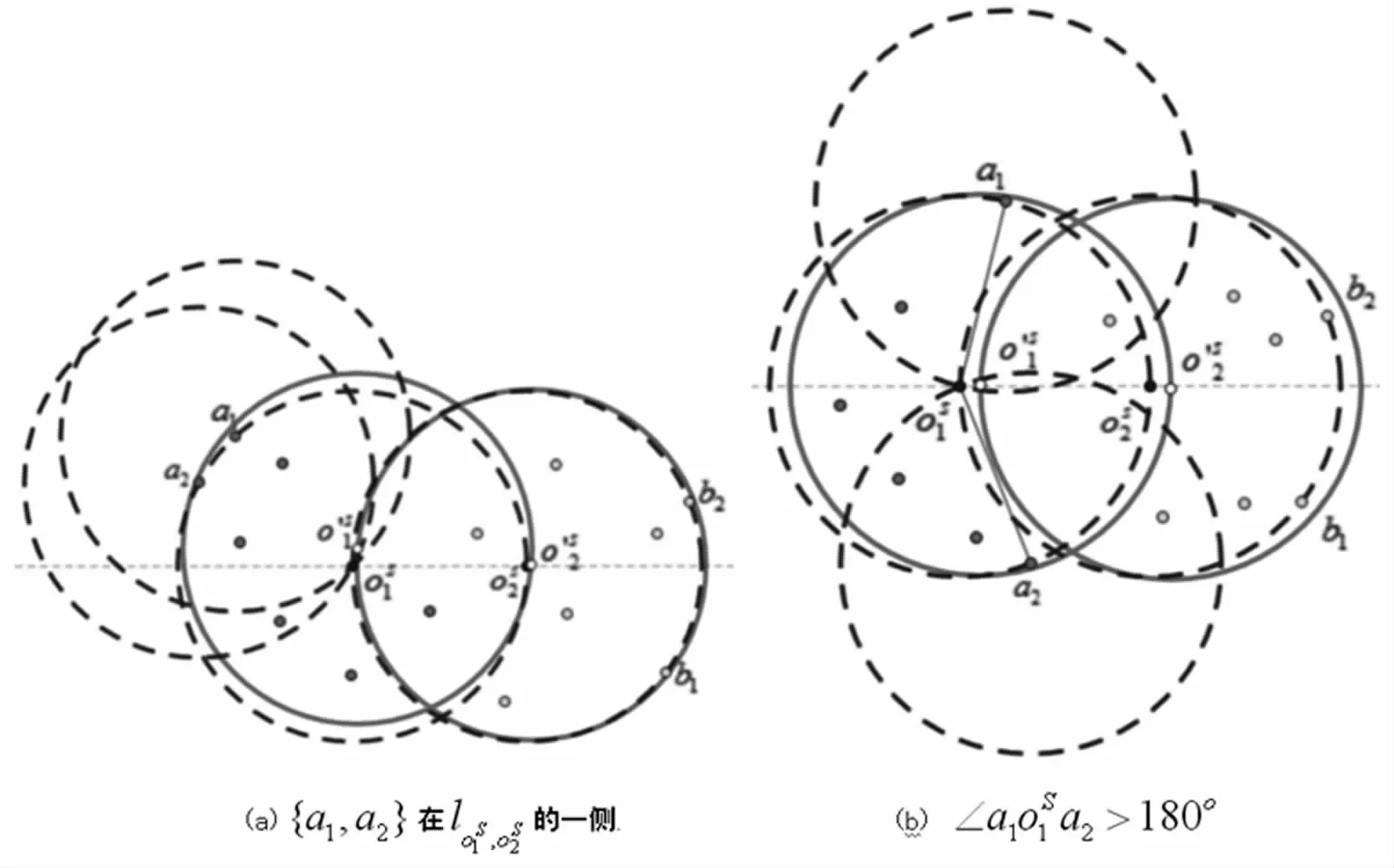
圖3 引理3說明

3 兩動態中心包之間最近距離變化分析

本節對兩個動態中心包之間最近距離的幾何結構性質進行分析。對給定點集P，Huang等人發現在半徑的變化過程中，P的中心包的組合性質與點集的最遠點Voronoi圖緊密相關（即性質4）。基于這個重要的性質，他們提出連通二中心問題可以在接近平方級別的期望時間內求解［11］。然而，在該問題的子算法中，牽扯到對兩個點集的中心包（假設兩個點集分別含有m和n個點）在同一個半徑r的變化過程中，這兩個中心包的組合性質不發生變化時如何求解最優半徑。他們給出該問題可以在O（log2（m+n））的時間內通過設計并行算法來求解。事實上，通過運用一些幾何性質，這個子問題可以在常數時間內求解，并且不需要運用并行計算，同時該算法可以完美求解最小最大二點集覆蓋問題。

注意到，對最優解幾何結構的第二種情況，只需要找到一個臨界半徑，滿足在這個半徑下CHr（P1）和CHr（P2）之間的最近距離等于該半徑即可。為了解決該問題，本節提出以下三個關鍵引理。對兩個點集P和Q，在同一個半徑r下，記這兩個中心包之間最近距離的控制點分別為s1和s2。首先給出第一個引理。

引理4若s1和s2分別在CHr（P）和CHr（Q）的一條弧上，則在半徑增加到r′的過程中，如果兩個中心包的組合性質不發生變化時，CHr′（P）和CHr′（Q）之間最近距離的控制點仍在對應兩個弧上。

證明記s1和s2分別在弧ar和弧br上。連接s1和s2，作兩條直線l1和l2垂直于ls1，s2。此時有l1與弧ar相切，l2與弧br相切（見圖4（a））。由中心包的凸性，可以得到當半徑增加到r′時，CHr′（P）和CHr′（Q）之間最近距離的控制點仍在弧ar′和弧br′上（見圖4（b））。

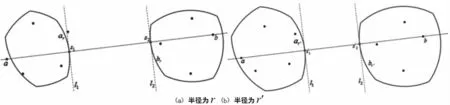
圖4 引理4說明，其中r＜r′，s1和s2均在弧上

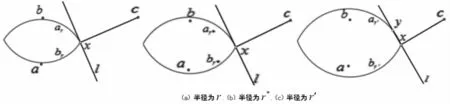
圖5 性質5說明，其中r＜r*＜r′，r*是臨界半徑，此時l與弧ar*相切

在給出第二個關鍵引理之前，先給出一個性質并加以證明：

性質5給定三個點｛a，b，c｝和半徑r，記x為弧ar和弧br的交點，l為過點x且垂直于lc，s的直線。如果l與弧ar僅有一個交點x，與弧ar′有不止一個交點（r＜r′），則一定存在一個臨界半徑r*，使得l與弧ar*相切。

證明當半徑為r時，直線l與弧ar相交于x點（見圖5（a））；當半徑為r′時，l與弧ar′相交于x和y點，同時注意到此時有y在弧ar′上（見圖5（c））。因此，隨著半徑的增加，可以得到a點從直線lc，x的一側連續移動到另一側，則一定存在一個臨界半徑r*使得｛a，c｝和x是共線的。這時，l與C（a，r*）相切（見圖5（b））。

由上述事實，給出第二個關鍵引理。

引理5假設s1為弧ar和弧cr的交點，s2在弧br上，其中｛a，b，c｝為圓心。在半徑從r增加到r′的過程中，如果兩個中心包的組合性質不發生變化，則這兩個中心包CHr′（P）和CHr′（Q）之間的最近距離對應的兩個控制點有如下三種情形：（1）仍然是一個為弧ar′和弧cr′的交點，另一個在弧br′上；（2）一個在弧ar′上，另一個在弧br′上；（3）一個在弧cr′上，另一個在弧br′上。

證明令s1′和s2′為CHr′（P）和CHr′（Q）之間最近距離的兩個控制點，由引理2，有｛b，s1，s2｝三點共線。連接s1和s2，過s1和s2分別作l1和l2垂直于ls1，s2，則有l2與弧br相切。因為在半徑增加到r′的過程中，兩中心包的組合性質不發生變化，則有：如果沒有弧與l1相交，則由于變化過程拓撲結構不發生變化，兩中心包最近距離的控制點仍舊落在弧ar′和弧cr′的交點以及弧br′上；否則，由于中心包的凸性，只會有CHr′（P）的一條弧與l1相交（不可能有大于一條弧與l1相交，如此做中心包則不為凸），不失一般性，假設弧cr′與l1相交。

接下來證明只有在弧cr′上的點有可能是距離弧br′最近的點。由于在半徑增加的過程中，弧cr′與l1產生了第二個交點（除去s1′），由性質5可以得到，一定存在一個臨界半徑r*，使得弧cr*與l1相切。這時中心包CHr*（P）和CHr*（Q）最近距離的兩控制點均在兩條弧上，再由引理4，?r′≥r*，CHr′（P）和CHr′（Q）最近距離的兩控制點一定一直在兩條弧上（即當r′≥r*時，此時與引理4情況相同）。圖6給出一個例子，其中r1＜r2＜r3，r2是臨界半徑。當半徑r′＞r2時，兩個中心包之間最近距離的兩控制點為一個在弧cr′上，一個在弧br′上。同理可證弧ar′與l1相交的情況。

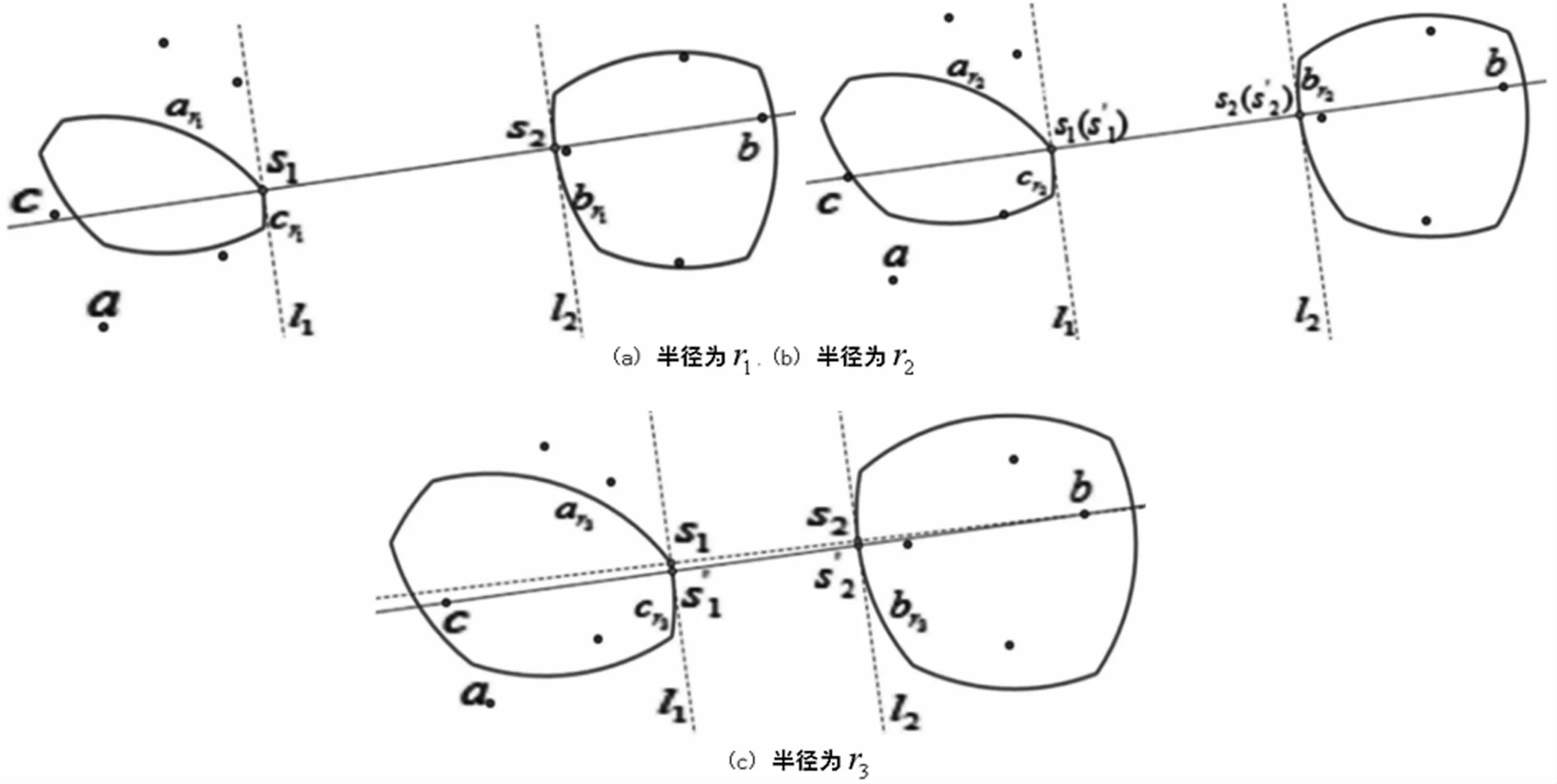
圖6 引理5示例，r1＜r2＜r3，r2是臨界半徑。l1與弧cr2相切，s1′在弧cr3上，s2′在弧br3上

最后給出第三個關鍵引理。

引理6記s1為弧ar和弧cr的交點，s2為弧br和弧d r的交點，其中｛a，b，c，d｝為圓心。在半徑從r增加到r′的過程中，如果兩個中心包的組合性質不發生變化，則這兩個中心包CHr′（P）和CHr′（Q）之間最近距離對應的兩個控制點有如下三種情形：（1）一個在弧上cr′，另一個在弧上br′；或者一個在弧ar′上，另一個在弧d r′上；（2）一個是弧ar′和弧cr′的交點，另一個在弧br′或弧d r′上；或者一個是 弧br′和 弧d r′的 交 點，另 一 個 在 弧ar′或 弧cr′上；（3）一個是弧ar′和弧cr′的交點，另一個是弧br′和 弧d r′的 交 點。

證明令s1′和s2′為CHr′（P）到CHr′（Q）最近距離的兩個控制點。連接s1和s2，過s1和s2分別作l1和l2垂直于ls1，s2。當半徑增加到r′時，由于兩個中心包的組合性質不發生變化，只會分別有CHr′（P）到CHr′（Q）的一段弧與l1和l2相交。接下來給出，如果弧cr′與l1相交，則只可能弧br′與l2相交。否則，假設弧d r′與l2相交，記這時CHr′（P）到CHr′（Q）最近距離的兩控制點為u和v，其中u在弧cr′上，v在弧d r′上。由于兩個中心包的半徑增加速度是一致的，并且由中心包的凸性，u和v之間的距離不可能小于d（）（否則中心包不為凸，或者其中一個中心包每條弧增長速度不一致），因此，弧d r′不可能與l2相交。同理可以證明如果弧ar′與l1相交，則只可能弧d r′與l2相交。隨著半徑繼續增加，會發生如下幾種情況。

情況1在半徑增加到r′的過程中，存在兩個臨界半徑和），其中當半徑增加到時，弧cr*1與l1相切，當半徑增加到時，弧br*2與l2相切。則根據半徑增加過程中兩個中心包的組合性質不發生變化，?r1≤，CHr1（P）和CHr1（Q）之間最近距離控制點為弧ar1和弧cr1的交點以及弧br1和弧d r1的交點；?，由引理5，CHr2（P）和CHr2（Q）之間最近距離的兩控制點一個在弧上，另一個為弧br2和弧d r2的交點；，由引理4，CHr3（P）和CHr3（Q）之間最近距離的兩控制點一個在弧cr3上，一個在弧br3上。此時，有lb，c與CHr3（P）和CHr3（Q）在弧cr3和弧br3均有交點，并且兩交點即為兩中心包最近距離控制點。圖7給出一個例子，其中r1＜r2＜r3＜r4，r2和r3為臨界半徑。當r＝r2時，l1與弧cr2相切；當r＝r3時，l2與弧br1相切；當半徑繼續增加到r4，則兩中心包的最近距離控制點s1′和s2′分別在弧cr4和弧br4上。

情況2在半徑增加到r′的過程中，假設存在一個臨界半徑r*。當半徑增加到r*時，l1與弧ar*和弧cr*均不相交，而l2與弧br*或弧d r*其中之一相切（l1與弧ar*或弧cr*其中之一相切，l2與弧br*和弧d r*均不相交的證明類似），則在半徑從r增加到r′的過程中，CHr′（P）與CHr′（Q）的最近距離的控制點一個為弧ar′和cr′的交點，另一個在弧br′上或弧d r′上（當r′≥r*），或者為弧br′與弧d r′的交點（當r′＜r*）。

情況3在半徑增加到r′的過程中，如果l1與弧ar′和弧均不相切，l2與弧和弧d r′均不相切，則在半徑增加過程中，CHr′（P）與CHr′（Q）之間最近距離的兩控制點仍為兩個弧的交點。至此，完成了對引理的全部證明。

圖7 引理6示例，r1＜r2＜r3＜r4，r2和r3為臨界半徑，當r＝r2時，l1與弧cr2相切；當r＝r3時，l2與弧br3相切；s1′在弧cr4上，s2′在弧br4上

4 算法設計與分析

這一節給出最小最大二點集覆蓋問題的確定性算法設計并分析算法復雜性，具體算法流程見Algorithm 1。

算法第1行計算點集P1和P2的最小覆蓋圓［18］，這部分可以在O（m+n）的時間內完成。

算法第2行到第3行，檢查是否滿足d（o1，o2）≤max｛r1，r2｝。如果是，則已然得到最優解。該檢測可以在常數時間內完成。

算法第5行計算一個點到一個中心包的最近距離，這一步可以在O（log（m+n））的時間內求出［19］。

算法第6行到第7行，檢查是否滿足min｛d1，d2｝≤max｛r1，r2｝。如果是，則已然得到最優解。該檢測同樣可以在O（log（m+n））常數時間內完成。故第5行到7行總共可以在O（log（m+n））的時間內完成。

算法第9行到第12行，是在如果上述兩種情況都不滿足的情況下，第9行首先分別計算P1和P2的最遠點Voronoi圖，該過程可以在O（mlogm）和O（nlogn）的時間內完成。

算法第10行分別計算P1和P2的臨界半徑，這個過程可以在O（mlogm）和O（nlogn）的時間內完成。

算法第11行計算最優解區間，將這兩個點集的所有臨界半徑合并排序，這可以在O（（m+n）log（m+n））的時間內完成；對每一個臨界半徑，可以在O（m+n）的時間內求出兩個點集的中心包［3］，在O（log（m+n））的時間可以求出這兩個中心包之間的最近距離［19］。因此，可以通過二分查找，在O（（m+n）log（m+n））的時間內找出一個包含最優半徑的臨界區間（rl，rh］。在該半徑區間內，隨著半徑的變化兩中心包的組合性質不會發生變化，同時滿足當半徑取rl時，中心包CHrl（P1）和CHrl（P2）之間的最近距離大于rl，當半徑取rh時，中心包CHrh（P1）和CHrh（P2）之間的最近距離小于rh。

算法第12行求解最優圓心及半徑，在文獻［11］中，Huang等人給出求解最優半徑需要通過并行計算的方法在O（log2（m+n））的時間內求解。由引理4、引理5和引理6可以設計算法并得出最優半徑可以在常數時間內求解。當r∈（rl，rh］，兩個中心包CHr（P1）和CHr（P2）變化過程中其組合性質不發生變化。記s1和s2是中心包CHrh（P1）和CHrh（P2）之間最近距離的控制點，這里分三種情況進行分析，其符號表示與上一節相同：

情況1若s1和s2分別是弧arh和弧crh，弧brh和弧d rh的交點。?r∈（rl，rh］，一定滿足CHr（P1）和CHr（P2）之間最近距離的控制點分別是弧ar和弧cr，弧br和弧d r的交點。因此只需要找到兩個點滿足這兩點之間距離以及兩點分別到｛a，c｝和｛b，d｝的距離全部相等，記這兩個點為所求圓心即可。該計算在常數時間內即可完成。

情況2若s1和s2其中之一在弧上，不失一般性，假設s2在弧brh上。?r∈（rl，rh］，CHr（P1）的控制點一定是弧ar和弧cr的交點，但是CHr（P2）的控制點有可能在弧br上，也可能是弧br和弧d r的交點。因此，需要通過5次計算：不僅需要找到兩點滿足兩點之間距離以及兩點分別到｛a，c｝和｛b，d｝的距離全部相等，還需要找到兩點滿足兩點之間距離以及兩點分別到｛a，c｝和b（｛a，c｝和d，a和｛b，d｝，c和｛b，d｝）的距離全部相等，在滿足的結果中找出距離最小的兩點作為圓心即可。

情況3若s1和s2均在弧上，不失一般性，假設s1和s2分別在弧ar和弧br上。?r∈（rl，rh］，有如下幾種可能：CHr（P1）和CHr（P2）的控制點可能在弧ar和弧br上；可能一個控制點在弧ar上，另一個為弧br和弧d r的交點；也可能一個控制點為弧ar和弧cr的交點，另一個在弧br上；或者一個控制點為弧ar和弧cr的交點，另一個為弧br和弧d r的交點。因此，需要通過7次計算：不僅需要找到兩點滿足兩點之間距離以及兩點分別到｛a，c｝和｛b，d｝的距離全部相等，還需要找到兩點滿足兩點之間距離以及兩點分別到｛a，c｝和b（｛a，c｝和d，a和｛b，d｝，c和｛b，d｝）的距離全部相等，以及線段la，d和lb，c的兩個三等分點。接著檢測計算出的兩點到各自點集的最遠點距離是否等于兩點之間距離，最后在滿足的結果中找出距離最小的兩點作為圓心，因此在臨界區間內找出最優半徑可以在常數時間內完成。故算法第9行到到12行總共可以在O（（m+n）log（m+n））的時間內完成。

綜上所述，可以得到：

定理給定分別包含m和n個點的兩個平面點集P1和P2，最小最大二點集覆蓋問題可以在O（（m+n）log（m+n））時間內求解。

5 結論與展望

本文考慮最小最大二點集覆蓋問題并給出時間復雜性為O（（m+n）log（m+n））的確定時間算法，其中求解最優半徑過程改進了Huang等人提出的并行算法。因為無論如何算法設計一定需要涉及排序這一操作［20］，而排序時間至少為O（（m+n）log（m+n）），因此本文設計的算法是目前為止最好的算法，并且不需要運用并行計算，大大減少了計算規模。而如果考慮兩個圓覆蓋一個含有n個點的點集情況，由于需要對點集進行分割，目前最好的算法仍然是Huang等人提出的O（n2logn）期望時間算法，而該問題的確定時間算法復雜性為O（n3logn）。因此，針對該問題，改進其算法的計算復雜性還是很有希望的。