基于韌性度的低軌衛星通信網絡抗毀性度量及優化

邵瑞瑞， 方志耕， 劉思峰， 游偉青， 聶媛媛， 高 素

（1.南京航空航天大學 經濟與管理學院，江蘇 南京211106；2.江蘇省國家密碼管理局，江蘇 南京210013；3.中國空間技術研究院 通信衛星事業部，北京100094）

0 引言

我國疆土遼闊，自然災害較多，經濟發展迅速但發展很不平衡，同時面臨著嚴峻的國內外安全及治安形勢。雖然電信業在近年來得到飛速發展，但是受地理環境和經濟因素的制約，地面通信網絡只覆蓋了國土面積的約15%，且在重大自然災害的搶險救災、遠海、高緯度地區沒有通信能力，全球范圍的維和、救援以及科學考察、資源運輸等缺乏主導的通信網絡，信息安全問題存在重大隱患，建立我國自主可控的衛星移動通信系統成為亟需解決的問題［1］。低軌道（Low Earth Orbit，LEO）衛星移動通信系統具有信號傳播距離短，鏈路損耗和傳播時延小，采用蜂窩通信、多址、點波束、頻率復用等相對比較成熟的技術，實現了真正意義的全球覆蓋［2］。因而，低軌衛星通信將成為未來衛星移動通信的主要發展方向。衛星通信網絡與傳統的地面通信網絡相比，在應用場景上有很大的不同，衛星布置在軌道面上有其自身的工作壽命，與此同時還可能受到外界的攻擊，其外部環境相對苛刻，使得其抗毀性的研究成為低軌衛星通信網絡技術的核心問題。

網絡抗毀性是指網絡中的節點或邊發生自然失效或遭受故意攻擊時，網絡拓撲結構保持連通的能力［3］。在低軌衛星通信中，用無向連通圖來表示通信網絡，圖的頂點代表低軌衛星星座中的衛星節點，邊代表無線通信鏈路。在此數學模型下，人們開始討論抗毀性的有關測度。眾所周知，網絡的抗毀性與其連通性有十分密切的關系，因而早期的研究主要集中在對圖的點連通度和邊連通度這兩個參數的分析［4］。而連通性僅描述了網絡遭受破壞的難易程度，而沒有考慮網絡被破壞后剩余網絡的連通能力。鑒于此，一些新的抗毀性參數被引入來解決這一困難，如堅韌度、離散數、完整度、韌性度［5～8］。文獻［8］提出的韌性度指標綜合了網絡被破壞的難易程度、被破壞后連通分支的規模、數目，更精細地度量網絡的抗毀性。孫成雨等［9］提出韌性度作為網絡抗毀性的指標，利用改進二進制粒子群算法求解點韌性度，驗證了方法的有效性。在網絡的抗毀性研究中，低軌衛星通信網絡必須考慮節點移動和切換造成的影響，這就為低軌衛星通信網絡抗毀性的研究提出了新的挑戰。彭興釗等［10］考慮了加權網絡在不同攻擊策略下的級聯抗毀性，分析了隨機攻擊與惡意攻擊下的網絡抗毀性問題。蔣瑞［11］研究了星上路由策略，提出切換是影響系統整體性能的關鍵因素，通過信道預留與接入控制策略來降低通話中斷的概率。Matar EDH等［12］開發了一個分析框架，用于評估完全共享（CS）與低地球軌道-移動衛星系統（LEO-MSS）中多類業務的兩種不同切換優先級方案的性能，開發了保護信道和切換請求方案排隊的組合。Mirzasoleiman B［13］等在加權網絡中研究了級聯故障的容差，考慮了三種加權策略對鏈路負載、網絡性能的影響。

從已有的抗毀性文獻可以看出，低軌衛星通信網絡抗毀性的研究主要集中在不同攻擊策略、路由策略和鏈路容量的優化設計上，并且都是考慮無權或者邊加權某個時刻的抗毀性，在考慮某個時間段內的抗毀性及其改進的問題上顯得明顯不足。本文通過考察網絡抗毀性的一個良好參數韌性度，結合低軌衛星的移動與切換模型來度量低軌衛星通信網絡在某個時刻及某個時間段的抗毀性，與此同時通過對切換模型中關鍵信道的賦權，求得了賦權韌性度下的抗毀性，實現了對低軌衛星通信網絡抗毀性的度量與優化。

1 相關理論

低軌衛星通信系統（簡稱LEO星座系統）主要是指軌道高度小于5000千米的一組或一群衛星相互協同工作，共同提供通信服務的衛星通信系統［14］。衛星軌道的形狀和高度對衛星星座的覆蓋性能有非常大的影響，是確定完成對指定區域覆蓋所需的衛星數量和系統特性的一個非常重要的因素。按照衛星軌道的形狀分為圓軌道和橢圓軌道，從軌道傾角的角度出發，衛星軌道分為赤道軌道、極地軌道和傾斜軌道。從軌道高度的角度出發，可以將衛星軌道分為低地球軌道LEO（Low Earth Orbit）、中地球軌道MEO（Medium Earth Orbit）、靜止/同步軌道GEO/GSO（Geostationary/Geosynchronous Orbit）和高橢圓軌道HEO（Highly Elliptical Orbit）。

低軌衛星通信網絡的抗毀性需要考慮衛星的移動、星間鏈路的不斷切換帶來的影響，確保網絡的連通性和關鍵功能。當網絡遭受攻擊時，拓撲結構隨時可能變化，要求其仍然能夠完成必要的通信任務。抗毀性模型中相關參數及理論定義如下：

定義1韌性度（Cozzens等人［8］）

設G（V，E）是一個無環無重邊的簡單圖，V為頂點集，S為割點集，S?V，E為邊集。

其中，割點是指在圖G中刪去一個節點S后，圖G的連通分支數增加，即ω（G-S）＞ω（G），則節點S為G的割點。｜S｜表示割點集S中節點的數量，G-S表示圖G去除割點及其邊后剩余的圖，ω（G-S）表示G-S的連通分支數，τ（G-S）表示G-S最大連通分支的頂點數。

定義2賦權韌性度

設（G，W）是一個點賦權完全連通圖，其賦權韌性度定義為：

其中，τW（G-S）表示G-S各連通分支頂點權和的最大值，W（S）＝ΣW（v）。

2 基于韌性度的低軌衛星通信網絡抗毀性模型構建

2.1 建模思路和原理

在設計低軌衛星通信網絡的時候，為了保證其有效運行，設計者既要考慮網絡內部節點發生失效或在受到攻擊時能維持通信要求不易被破壞，又要考慮一旦網絡遭到破壞后能夠容易修復而承受較小的代價。衛星在軌道內高速移動，為了確保通信的連續性必須進行切換，包括波束切換、衛星切換以及星間鏈路的極區切換，衛星的移動和切換是實現低軌衛星通信的關鍵因素。

通過對低軌衛星移動的分析得到其移動模型，進而求得其簡化拓撲結構圖為Gx，Gy，…，同理，通過對衛星切換模型的分析得到其簡化拓撲結構圖為Gu，Gv，…，進而對某時刻的抗毀性以及某一段時間內的平均抗毀性進行度量。因此，低軌衛星通信系統抗毀性的建模可以通過對衛星的移動和切換模型分析，對抗毀性進行度量及優化的過程，如圖1所示。

圖1 低軌衛星通信網絡抗毀性建模

2.2 低軌衛星通信網絡的移動模型

不同的移動模型對網絡的性能、網絡的運行成本以及網絡的安全性都會產生不同的影響。對移動模型的研究和分析有助于整個衛星星座的設計，對衛星通信網絡的安全性及韌性度、抗毀性等性能的改善起到推動作用。因此，分析低軌衛星通信網絡的移動模型以及如何度量不同移動模型的抗毀性，是衛星星座設計和實現網絡通信所要考慮的首要問題。

衛星的移動遵循特定的軌道，根據軌道中的衛星間是否存在星際鏈路分為有星際鏈路衛星星座（Iridium系統）和無星際鏈路衛星星座（Globalstar系統、Teledesic系統）等。所謂星際鏈路，是將星座系統中相鄰衛星連接起來的通信鏈路，使衛星有機地聯系在一起。星際鏈路的建立使得系統可單獨組網，降低了對地面網絡的依賴，成為全球移動通信系統不可替代的重要組成部分，引起了世界各國的廣泛關注，也是我國未來衛星通信網絡的重要組成部分［15］。

簇首移動模型（Cluster head movement model，CH2M）是衛星群構成的星座圍繞地球按預定的軌道周期性的運行，如果將每個軌道面看成一個簇，且每個簇存在一個簇首衛星，簇首衛星的特性代表了整個軌道衛星的移動行為。因此，可以看成簇首衛星帶著本簇的衛星在預定的軌道內圍繞地球運動。CH2M模型的衛星移動情況如圖2和圖3所示，其特點如下：

圖2 衛星移動模型

圖3 衛星位移示意圖

（1）當簇首在軌道平面內運動時，會將相應的移動參數通過星際鏈路傳遞給周圍的衛星。若簇首發生位移A→C，B→D，簇首的移動方向即由加上位移矢量得到新的位移方向

（3）同一軌道平面內的相鄰衛星要保持一個安全距離SD（safe distance），即?i，?j，?t，Dij（t）≥SD。

Manhattan移動模型（曼哈頓移動模型）是根據紐約市曼哈頓島的城市地圖抽象而來的，具有規則的格狀拓撲結構。在該模型下，假定節點隨機分布于城市街道中，城市的街道由一些水平和垂直的街道組成，并且節點只能在水平和垂直的街道上移動。由于與星座網絡的拓撲結構非常類似，因而可以用來描述衛星網絡的移動情況，如圖4所示。

圖4 星座網絡的曼哈頓移動模型

2.3 低軌衛星通信網絡的切換模型

在LEO衛星通信系統中，衛星在預定的軌道內繞著地球高速的公轉，同時地球在自轉、用戶在移動。由于衛星的運動速度遠高于地球的自轉和用戶的移動速度，成為引起呼叫切換的主要因素，用戶可視為相對“靜止”狀態。在陸地蜂房網中，基站是靜止不動的，切換主要是由于移動用戶的無規律運動，而在LEO衛星通信系統中，衛星起到了類似基站的作用，切換主要歸因于“基站”有規律的運動。由于兩種網絡中引起切換的因素與規律不同，因而不能用陸地蜂房網切換模型來分析LEO衛星通信系統的切換問題，必須建立適用于低軌衛星通信網絡的切換模型。

低軌衛星星座中的切換可分為波束切換（圖5）、衛星切換（圖6）和星間鏈路的極區切換（圖7）三種［16］。衛星在跨越極點時，相鄰軌道面之間的衛星相鄰關系產生交錯，必須關閉軌道面間ISL和部分波束，導致星座網絡拓撲結構發生變化。

圖5 波束切換

圖6 衛星切換

圖7 極區切換

在低軌衛星通信網絡中，衛星和地面移動終端之間的相對運動，使得部分呼叫在通信過程中需跨越邊界，此時系統必須將這類呼叫切換至相鄰的、具有空閑信道的衛星繼續服務。當空閑的信道同時接收原始呼叫和切換呼叫時，它們獲得信道服務的機會是等可能的。當所有的信道都處于繁忙狀態時，到達的切換呼叫不能被分配信道，對于用戶而言則表現為通話中斷，因而，低軌衛星通信網絡切換失敗的概率等于呼叫阻塞的概率。在移動通信系統中，除了通話結束信道被釋放外，由于衛星運動造成單元小區不再覆蓋當前用戶，用戶呼叫被迫切換，先前占用的信道也將被強制釋放，切換狀態轉移圖如圖8所示：

圖8 低軌衛星通信網絡切換狀態轉移圖

其中，Ei表示信道的占用情況，λt與μc表示切換狀態的呼叫到達率，N為信道總數。當所有信道均被分配完畢后，新的原始呼叫與切換呼叫被會被阻塞。

2.4 低軌衛星通信網絡抗毀性的求解

抗毀性（Invulnerability）是指系統在失效的情況下，能夠繼續保持正常工作的能力。沿用美國國土安全部的概念，韌性（Resilience）可以定義為系統預防和適應變化條件，并且承受這些擾動并迅速恢復的能力［17］。Francis與Bekera等對現有韌性定義的總結，認為“抵御能力、吸收能力與恢復能力”是韌性系統的三個主要特征［18］。抵抗擾動及擾動后的恢復能力是韌性理念的兩個核心指標，可以說，一個系統的韌性越強，其抵御擾動、面臨打擊時的抗毀性也越強。與此同時，在文獻［8］和［9］中都提出韌性度作為一種新的抗毀性參數，對于解決抗毀性僅注重網絡遭受破壞后的連通性這一難題提出了新的解決方案。因此，本文引入韌性度來度量低軌衛星通信網絡的抗毀性。

在低軌衛星通信網絡中，衛星按照一定的軌道周期高速移動，為了保持通信的連續性，需要不斷的進行切換，不停的移動需要不斷的切換，移動與切換伴隨了低軌衛星通信的全過程。如果將衛星的移動看成0時刻，切換看成T時刻，通過對移動和切換模型的分析，對［0，T］內低軌衛星通信網絡的抗毀性進行度量。

在［0，T］內，做以下兩點假設：

a）若低軌衛星通信網絡在t時刻的移動／切換模型有n種（G1，G2，…，Gn），每種移動／切換模型出現的概率為P1，P2，…，Pn，且P1+P2+…Pn＝1。以此類推，網絡在其它時刻也有類似的特點，且整個網絡是保持連通的。

b）對于韌性度的求解只考慮節點（衛星）出現故障的情況。

根據上面的假設，可以求得由N個衛星組成的低軌衛星通信網絡G在時刻t時的抗毀性：

其中，p1，p2，…，pn為低軌衛星通信網絡G在t時刻每種移動／切換模型出現的概率，T（G1），T（G2），…，T（Gn）為低軌衛星通信網絡G在t時刻移動／切換模型為G1，G2，…，Gn時的韌性度。

低軌衛星通信網絡G在［0，T］內的平均抗毀性為：

由式子（3）可知，某時刻低軌衛星通信網絡的抗毀性與該時刻的韌性度有關，而韌性度值跟該時刻的移動／切換模型有關。由于移動／切換模型的出現的可能性不同，因而在考察其抗毀性時引入了每種移動／切換模型出現的概率。式（3）求得的抗毀性值K（G）t越大，網絡的抗毀性就越強。式（4）是某時間段內的平均抗毀性越大網絡抗毀性就越強。

2.5 低軌衛星通信網絡抗毀性的優化

通過對低軌衛星通信網絡切換模型的分析可知，在繁忙的信道環境下，原始呼叫和切換呼叫都不能被分配信道，已經接入的用戶呼叫也會中斷，這顯然與用戶通信要求是相背離的。因此，需要對低軌衛星通信網絡的切換模型進行優化，減少切換的阻塞概率，尤其應避免已經建立的通話被中斷。

在優化切換模型中，通過對低軌衛星通信網絡切換模型韌性度的求解，找出使網絡的韌性度值達到最大的割點集所在的節點（假設有Nq個，且Nq∈［2，n-2］）為關鍵信道，將其專門用于分配切換呼叫。與此同時使用排隊門限和定義緩沖區對切換呼叫進行先入先出的隊列管理，通過緩沖區的設置達到延長呼叫切換等待時間，增大切換成功的概率，在此主要通過對信道進行賦權來體現其改進。要想賦權信道發生堵塞，對于攻擊者來說要花費更高的代價。剩余的N-Nq個信道按原切換模型進行分配，當原始切換和切換呼叫到來時，首先分配N-Nq個信道，當N-Nq個信道被分配完畢后，切換呼叫到達時，使用Nq個專用信道，不再向原始呼叫分配信道。優化切換狀態轉移圖如圖9所示：

圖9 低軌衛星通信網絡優化切換狀態轉移圖

其中，λt與μc表示呼叫到達率，λq表示切換到達率，N為信道總數，狀態Ei表示信道占用情況和隊列容納情況，Nh表示緩沖等待隊列中切換呼叫的數目。

低軌衛星通信網絡的數據傳輸是依靠衛星節點來實現的，若網絡中存在核心衛星節點，如網絡割點，一旦這些衛星節點失效，將會嚴重影響通信網絡的整體連通度，甚至導致整個網絡的崩潰。因而，對切換模型的優化，可以通過對核心節點進行保護來提高網絡的抗毀性。對低軌衛星通信網絡優化的切換模型進行賦權，用賦權韌性度的值代替式（3）中的韌性度求得抗毀性值，進而根據式（4）求得平均抗毀性值。

3 案例分析

銥星（Iridium）是典型的低軌衛星移動通信系統，是美國Motorola公司于1986年提出的世界上第一個全球覆蓋的衛星通信系統。銥星系統主要由空間段和地面段組成，空間段是指衛星星座，包含6個軌道高度為780km的近極軌道面，每個軌道面11顆衛星，共有66顆衛星以及6顆備份星。地面段主要包括系統控制中心、關口站和用戶終端等。為了實現隨時隨地的個人通信并使衛星及其空中網可以獨立于地面的蜂窩通信網絡，銥星系統采用了具有星上交換功能的智能衛星，每一顆衛星都與其它衛星之間維持著星際鏈路ISL（Inter-Satellite Links）。星際鏈路ISL又分為不同軌道平面間星際鏈路（InterlSL）和同一軌道平面內星際鏈路（IntralSL），實現了真正意義上包括兩極地區的全球覆蓋。

3.1 銥星系統移動模型分析及其拓撲圖的構造

簇首移動模型（CH2M）中，每個軌道平面內的衛星以簇首為參照進行移動，衛星之間通過交互信息進行通信，而且這些衛星在當前時刻以某種方式相連著，下一時刻還是以類似的方式相連著。在銥星系統中，每個軌道面上11顆衛星等間距分布，其中，每個軌道面都是穿過極地的圓形軌道，軌道面傾角為86.4度，衛星通過軌道平面內的星際鏈路（IntralSL）互連。同一軌道面上，前后2顆衛星之間的星間鏈固定安全距離為4033km，且每個軌道面上有一顆備份星，那么在某個時刻衛星與衛星之間的連通關系可以用圖10來表示。

曼哈頓移動模型（Manhattan）模擬車輛、行人在Manhattan街道上移動的情況，其運動受到街道的限制，同一街道上的節點可以進行通信，不同街道間節點的通信要通過街道與街道交叉處節點的轉發進行通信。這與銥星系統中不同軌道平面間星際鏈路（InterlSL）有相似之處，所以該模型下某時刻的銥星系統衛星之間的通信可以用圖11來表示。

圖10 銥星系統CH2M簡化拓撲圖

圖11 銥星系統Manhattan移動模型下的簡化拓撲圖

3.2 銥星系統切換模型拓撲結構分析

圖12 銥星系統切換模型靜態邏輯拓撲結構

圖13 銥星系統波束切換和衛星切換簡化拓撲圖

圖14 銥星系統極區切換網絡拓撲圖

3.3 銥星通信網絡的抗毀性

在銥星通信網絡中，在t＝0時刻的移動模型拓撲結構如圖10和圖11兩種情況，其分別代表衛星在同一軌道平面內星際鏈路（IntralSL）和不同軌道平面間星際鏈路（InterlSL）上移動，在此認為其出現的概率相同。在t＝1時刻的波束切換和星間切換的拓撲結構為圖13所示，星間鏈路的極區切換如圖14所示，并且銥星衛星的軌道周期約100min，波束平均切換時間為1～2min，星間切換的時間平均為9min，星間鏈路切換時間間隔為162.69s和111.26s［21～23］。據 此 設 波 束 切 換 出 現的概率為0.57，星間切換出現的概率為0.08，星間鏈路的極區切換出現的概率為0.35。

根據2.4中提出的度量方法計算銥星系統在通信時的抗毀性以及平均抗毀性值。

a）先考慮t＝0時刻銥星通信網絡的抗毀性：

根據式（1）可以求得圖10和圖11的韌性度分別為：T（G）t＝0＝3.5，T（G）t＝0，且p1＝

由式（3）可 得：K（G）t＝0＝p1T（G1）t＝0+

b）再考慮t＝1時刻銥星通信網絡的抗毀性：

c）根據求得的低軌衛星通信網絡在t＝0，t＝1時刻的抗毀性值，根據式（4）可以求得此網絡在［0，1］內的平均抗毀性值：

（2）操作階段。操作階段包括以下任務：第一，為知識客戶提供知識搜索請求的終端用戶界面；第二，選擇與用戶請求相關的知識源進行知識源網絡配置；第三，對已有的知識和生成的知識進行選擇、獲取、融合以及確認；第四，為用戶提供請求結果；第五，存儲請求結果。

3.4 銥星通信網絡抗毀性的優化

圖13銥星系統波束切換和衛星切換簡化拓撲圖韌性度的求解過程及結果如表1所示。由于南北極地區人口資源少，銥星系統衛星覆蓋密集，且星間鏈路的極區切換導致星座網絡拓撲結構處于快速的變化中，為了簡化模型，在此僅對波束切換和衛星切換方式進行優化。

銥星通信網絡的優化步驟如下：

步驟1通過對銥星通信網絡切換模型韌性度的求解篩選出Nq個關鍵信道；

步驟2將Nq個關鍵信道首先用于確保切換呼叫，同時使用排隊門限和定義緩沖區對切換呼叫進行先入先出的隊列管理，為體現這些措施實現的效果，主要通過對對信道進行賦權；

步驟3度量賦權韌性度下銥星系統的抗毀性。

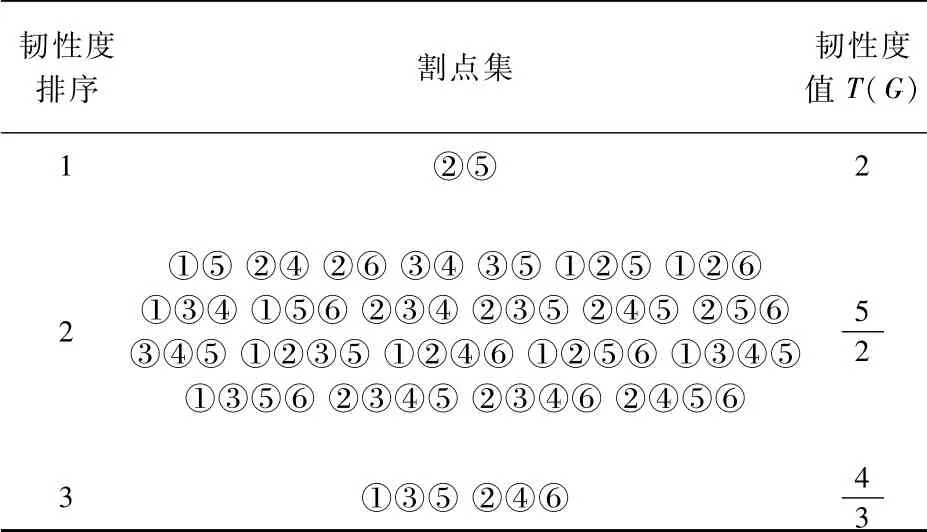
表1 銥星系統切換模型的韌性度

韌性度的大小反映網絡的抗毀性。從表1可知，當割點集為②⑤時，計算出的銥星系統切換模型的韌性度值達到最大，此時銥星通信網絡的抗毀性強，切換呼叫的成功率自然就高，如果將②⑤作為呼叫切換的專用信道，當專用信道遭受攻擊時對銥星系統的造成的影響也是最小的。對表1中的所有割點集統計各個節點出現的次數，如表2所示。從表2可知，②⑤一旦遭到破壞，對銥星系統的連通性影響最大，因而將②⑤作為N-Nq個信道全部分配完的補充信道，僅用于提高切換呼叫的成功率是合理的。

表2 所有割點集中各個節點出現的次數

現將②⑤專門用于切換呼叫信道，并使用排隊門限和定義緩沖區對到來的切換呼叫進行先入先出的隊列管理，為了更形象地體現切換呼叫的優化效果，通過節點賦權實現對銥星通信網絡抗毀性的優化。

所有割點集中各個節點出現的次數說明了節點的重要程度，為了提高網絡的抗毀性，在設計階段需要對重要的節點采取保護措施（如備份等），因而想要破壞它需要付出更大的代價。按照表2節點在割點集中出現次數的排序結果，同時結合切換呼叫的優化效果，對圖13銥星系統切換模型的賦權如圖15所示。

圖15 銥星系統優化切換模型賦權圖

3.5 仿真分析

對低軌衛星通信網絡的抗毀性模型，用Matlab來分析此模型中韌性度對某時刻抗毀性值的影響，用origin對銥星通信系統優化前后的抗毀性及平均抗毀性進行了對比，如圖16所示。

當低軌衛星通信網絡在［0，T］內的簡化拓撲結構只有n＝1種時，該網絡在t時刻的韌性度與抗毀性的關系如圖17所示。

圖16 銥星通信網絡優化前后對比

圖17 t時刻韌性度與抗毀性的關系

由圖16易知，通過對銥星通信系統切換模型的優化，網絡的抗毀性與平均抗毀性都得到了提升。根據圖17可知，當低軌衛星通信網絡只有一種拓撲結構時，任意時刻網絡的抗毀性跟拓撲結構的韌性度值有關，并且是一種線性關系，即隨著韌性度的增加，其抗毀性也增加。由于每個時刻的韌性度與抗毀性是一種線性關系，平均抗毀性是通過各個時刻抗毀性總和的平均數求得，所以平均抗毀性也是隨著韌性度的增加而增加，與韌性度也是一種線性關系。

4 結論

本文主要研究了低軌衛星通信網絡的抗毀性，提出一種基于衛星移動和切換為主導因素，通過韌性度的求解對某時刻的抗毀性以及某時段的平均抗毀性進行度量。首先分析了低軌衛星的移動模型和切換模型，然后構建了低軌衛星通信網絡抗毀性的求解模型，最后通過對切換模型的優化實現了對模型的改進，達到優化網絡抗毀性的目的。銥星通信網絡的實例表明，本文構建的模型不但可以對銥星通信網絡某時刻以及某時段的抗毀性進行度量，而且可以通過對關鍵信道的識別以及信道賦權優化網絡抗毀性，驗證了該模型的有效性，為抗毀性的度量與優化問題提供了新的解決思路。