基于條件模擬理論的波浪數值模擬

張 夢，柳淑學，李金宣，張昊宸

(大連理工大學 海岸和近海工程國家重點實驗室，大連 116024)

條件模擬是地質統計學中的一個概念。在地質統計學中，因研究對象是一種具有結構特征的隨機變量，對它進行數學模擬時要求保持一定的空間相關性，即保持實驗信息具有相同的協方差函數或變差函數，在地質統計學中稱非條件模擬(unconditional simulation)；如果再增加一個更嚴格的約束條件，將模擬條件化，即令在各觀測點處的模擬值等于該點的實測值，稱其為條件模擬(conditional simulation)[1]。

近年來，由于一些海上工程規模的龐大和工程問題的復雜性，其對波浪荷載精確程度的要求也越來越高。目前在實驗室中進行物理模擬主要是通過模擬頻譜，不能模擬波形。很多時候研究人員常常需要研究某一特定短波列或波群對建筑物產生的作用，且這段短波列包含于滿足某一特定波譜的隨機波列中，這往往需要進行逐波分析以找到滿足此條件的隨機波列，費時費力。因此如何有效地產生這樣的特殊波列對研究波浪對于復雜工程作用問題具有重要的意義。

起初，波浪模擬主要都是通過模擬頻譜的方式來實現的。Borgman[2]建立了線性波浪疊加法和線性過濾法，過濾法主要利用白噪聲濾波的方式對波浪進行模擬，線性疊加法中初相位隨機分布，因此也稱為隨機相位譜法。后來，人們發現有時是某種特殊的波列對建筑物產生主要的破壞作用[3]，因此需要模擬一些特殊波列。劉思等基于改進的波包譜[4]的經驗公式，建議了單向不規則波群的數值模擬方法[5]，但只是模擬了同時滿足頻譜及群性要求的波浪，并不是嚴格地模擬了不規則波列。Borgman[6]提出波浪的條件模擬概念，即在滿足波浪的統計特征情況下，人為加入一些約束，闡述了如何利用正態分布的條件概率理論，在時域上產生一段既包含特殊短波列，又屬于某一波譜的目標波列。但當計算波列的長度增大時，此方法暴露出一個很大的缺點：自相關函數矩陣越來越病態導致計算結果出現嚴重偏差。Spanos[7]建立的ARMA波浪模擬模型在計算時遇到同樣的病態Toeplitz矩陣。Medina和Sanchez-Carratala[8]對數值波浪模擬中的許多計算模型進行了比較，通過在波浪中加入白噪聲的方式很好地解決了這個問題。Gime′nez等[9]從上述方法得到啟示，并將其運用到條件波浪模擬中，解決了算法中出現的病態矩陣問題。Hudspeth等[10]在二維水槽中對目標波列進行了重現，同時從能量的角度討論了嵌入波列的參數對模擬產生的影響。

天然海浪波列中存在的極限波浪，是造成海洋工程建筑物破壞的主要因素之一，而波浪聚焦是目前實驗室產生極限波浪的主要方法，即讓不同方向、不同頻率的波浪在傳播過程中互相調制，使波能發生集中，形成極端大波。但是這樣模擬波浪的過程中畸形波的產生具有隨機性，因此如何實現在不規則波的波列中嵌入已知的畸形波過程，在特定地點和時間產生包含已知畸形波列的確定性模擬，亦是進一步提高物理模型試驗水平的需要。Oggiano等[11]基于數值二維水槽，針對一極限波浪過程，建立可以復演該過程的造波邊界條件，但其只是針對孤立的極限波浪過程，并非針對整個不規則波過程。Buldakov等[12]則對于給定的二維單向特定的極限波浪及其破碎型式進行了確定性的模擬研究，但是其針對的是短序列的波群序列，而非一完整的包含畸形波的不規則波序列。Pierella等[13]對于二維極限波浪，基于流函數理論，將其嵌入一不規則波波列，實現其在物理水槽中的確定性的模擬。

本文基于Borgman的條件模擬波浪理論，通過加入白噪聲的方式，解決了計算中因病態矩陣導致的數值不穩定問題，進而建立了二維數值波浪模擬程序，可在滿足某一特定波譜的隨機波列中，在任意合理時間點，嵌入某一特定波列后，產生的新的隨機波列仍然滿足上述特定波譜。分別以規則波和聚焦波為嵌入波列，研究了嵌入波的長度、周期、波高和嵌入點等對模擬波浪產生的影響。

1 基于條件模擬的波浪模擬方法

所謂條件波浪模擬，首先通過基于給定波浪參數和波浪譜，模擬生成一初始的隨機波列ηu(t)，可稱之為非條件模擬；之后在指定的時間點嵌入一段特殊的波列ηe(t)，從而形成新的同時仍滿足給定的波浪譜和統計特征參數的隨機波列ηc(t)。

對于初始的隨機波列ηu(t)，可采用非條件波浪模擬得到。即假定海浪可看作一平穩隨機過程，由無數多個不同的余弦波隨機疊加而成[3]

(1)

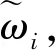
(2)

把代表M個區間內波能的各余弦波動疊加起來，即得不規則波的波面

(3)

為了在初始波列中某一時間點嵌入某一特定的波列，可將初始波列的波面ηu(t)前后分為3段，表示為{ηu-,vu,ηu+}T，其中vu代表將要被嵌入的短波列替代的部分，而目標波列可表示為{ηc-,vu,ηc+}T；若ve表示將要嵌入的波列，即要求

vc=ve

(4)

接下來就是如何求解ηc-、ηc+，使得所形成的新的波列既滿足所要求的波浪譜，同時嵌入已知的某特定波列。這里假設波浪的波面滿足正態分布，則由多向正態分布的條件概率公式可得

(5)

式中：C12T、C11-1為初始波列自相關函數矩陣的分塊矩陣，其表達式可參見Hudspeth等[10]，詳細證明可見Borgman[6]。

2 數值模擬及結果分析

2.1 嵌入規則波數值模擬結果分析

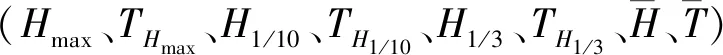
表1 初始波列參數Tab.1 Unconditional simulation wave parameters

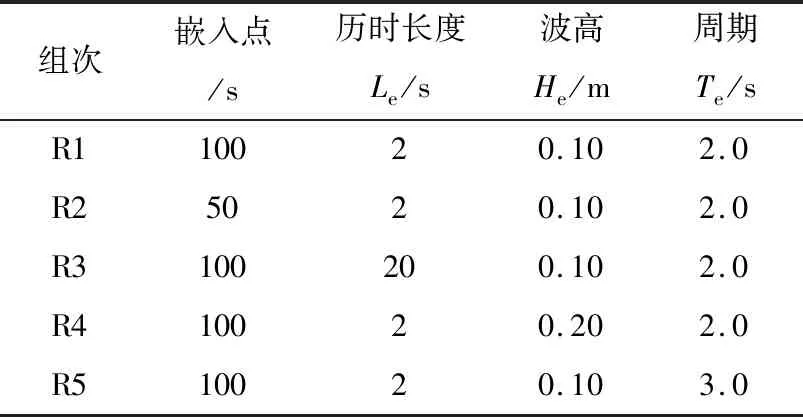
表2 嵌入規則波參數Tab.2 Embedded regular wave parameters

(6)

式中：ηu為初始波列的過程線；ηc為目標波列的過程線；N為序列長度；Hmax為初始波列的最大波高。需要說明的是，式(6)中誤差累加計算不包括嵌入波列的部分。

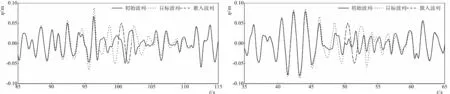
1-a 組次R1 1-b 組次R2

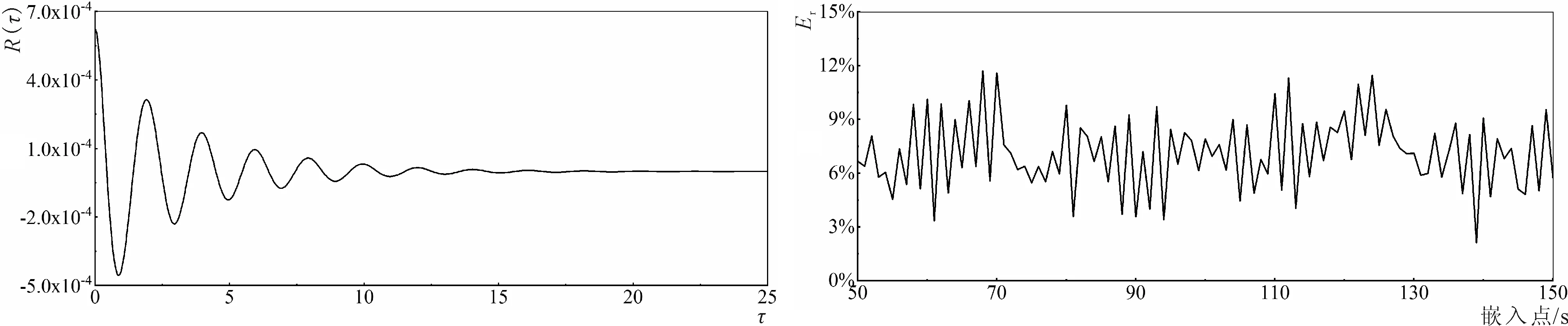
圖2 初始波列的自相關函數曲線圖 圖3 波面誤差隨嵌入點的變化(組次R2)Fig.2 Auto-correlation of the unconditional simulation wave Fig.3 Variation of RMS error coefficient with the embedded time point

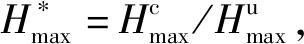
圖4 目標波列與初始波列特征波高的比值隨嵌入點的變化(組次R2) 圖5 目標波列與初始波列特征周期的比值隨嵌入點的變化(組次R2)Fig.4 Comparison of the variation of the ratios between the unconditional simulation and conditional simulation characteristic wave height with the embedded time point Fig.5 Comparison of the ratios between the variation of the unconditional simulation and conditional simulation characteristic wave period with the embedded time point

圖6為各組次目標波列與初始波列的波譜比較圖，表3為嵌入規則波后波列各統計參數計算結果。具體來說，從組次R1、R2的統計參數和譜對比來看，進一步說明嵌入點的改變對模擬產生的波浪分析結果影響不大；同樣，從組次R1、R3的結果對比來看，當嵌入規則波列的長度增大了9倍，但其統計參數和譜的變化亦較小，因此可以認為當嵌入規則波列的周期和波高與初始波列的有效周期和波高相差不大時，嵌入規則波列的長度變化不會對模擬波浪產生明顯的影響；從組次R1、R4的結果對比來看，嵌入規則波列的波高增大了1倍，而其統計有效波高參數和譜亦沒有產生很大的變化，但是如果嵌入的規則波波高較大或大于初始波列的最大波高時，新的波列的最大波高會大于初始波列的最大波高。

而從組次R1、R5的結果對比來看，嵌入波列的周期會對模擬得到的新的波列產生較大的影響。從圖1組次R5可以明顯看出，目標波列與初始波列相比，其在嵌入波列周圍產生了較大的特異波浪，從表3中也可以看到各統計波高明顯增大，從圖6組次R1、R5的對比可以看到，嵌入規則波后的波浪譜整體明顯變大。也就是說，嵌入規則波的周期與初始波列譜峰周期偏離越大，嵌入特定規則波后波浪的特征與初始波列特征相差就越大。

6-a 組次R1、R2 6-b 組次R1、R3

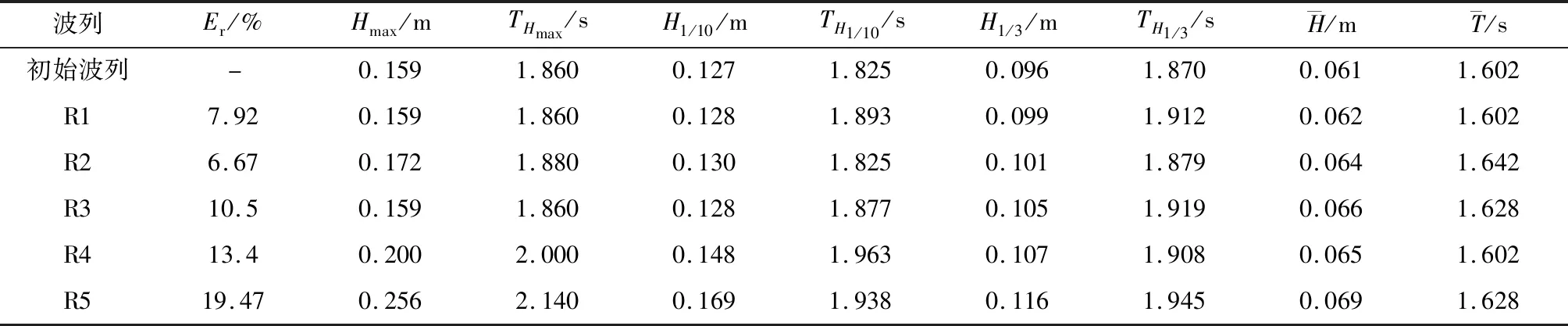
表3 嵌入規則波時初始波列和目標波列的統計參數表Tab.3 Statistical parameters of unconditional simulation and conditional simulation after embedding regular waves

綜合上述討論可以看出，當嵌入規則波列時，嵌入點、嵌入波列的長度和波高變化對初始波列的統計特征參數和譜的影響不大，可以認為條件模擬是有效的，但是當嵌入規則波的波高較大時，嵌入規則波后的波列的最大波高會增大。事實上，從某種程度上看，嵌入波列的周期變化也沒有對統計參數和譜產生較大的影響，但是由于嵌入波列的周期偏離了初始波列的有效周期，統計特性的不同使得初始波列產生類似“排斥”效應，從而在嵌入波浪附近產生了特異波浪。這種含有遠遠大于隨機波列有效波高的特異波的長波列不滿足常規波浪特征，因此嵌入波列的周期應與初始波列的周期基本一致。

2.2 病態矩陣問題

在上述計算過程中，有時會出現如圖7所示情況。圖7中7-a、7-b、7-c分別代表嵌入一個波高為0.1 m，周期分別為2.16 s、2.18 s、2.2 s，長度為一個周期的規則波。在周期改變很小的情況下，圖7-b的模擬結果卻出現了很大的波動。其原因是因為計算公式(5)中的矩陣C11有時為病態的，使得計算結果不穩定。Spanos[7]通過ARMA算法進行波浪模擬時遇到了相似的問題。根據Spanos和Mignolet[14]的研究，發現其原因是譜在低頻率時波浪譜密度值為0引起的。根據此特點，Medina和Sanchez-Carratala[8]通過在波浪譜中人為地加入白噪聲，從而很好地解決了這個問題。假定加入的白噪聲占總能量的ε，則新的譜為

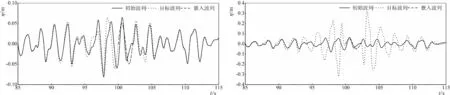
7-a Te=2.16 s 7-b Te=2.18 s

(7)

式中：fL、fH分別表示頻率的上下界，其取決于模擬波浪時在低頻和高頻處略去的波浪的能量占波浪總能量的比例[3]，本文取1%。雖然此種方法改變了原有譜形，但是Gime′nez等[9]認為無論是實驗室產生的波浪還是海面上記錄的波浪都存在著噪聲，因此當ε取得足夠小時，S*可近似等于S。圖7-d為取ε=0.000 5所計算得到的新結果，與圖7-b相比有了很大改善。本文所涉及到的譜的計算全部采用S*。

2.3 嵌入聚焦波數值模擬結果分析

2.3.1 二維聚焦波的產生方法(相速度法)[15]

聚焦波可通過模擬頻譜的方法產生。對于二維波浪，任一點處波浪自由表面可以表示為不同頻率和不同幅值的余弦波線性疊加后的結果，即

(8)

式中：aj為第j個組成波的幅值；kj為第j個組成波的波數；ωj為波角頻率；φj為j個組成波的初相位；N為組成波的總個數。kj和ωj滿足波浪的色散關系

(9)

式中：g和d分別為重力加速度和水深。若假定波浪在指定時刻t=tb聚焦于x=xb位置處，即各組成波在x=xb處波峰疊加，那么需滿足

cos(kjx-ωjt-φj)=1

(10)

則各組成波的初相位應滿足下式

φj=kjxb-ωjtb

(11)

此時，波浪的波面表達式為

(12)

由式(12)可以看出，對于給定的聚焦時間tb，聚焦點的坐標xb，頻率數N，影響波浪聚焦面參數主要為各組成波的幅值aj。通常把A定義為聚焦點處的波浪幅值，則有

(13)

則生成聚焦波浪組成波的幅值可以表示為

(14)

式中：頻譜S(f)為本文采用的JONSWAP譜。

2.3.2 數值模擬及結果分析

以聚焦點為中點向兩邊對稱截取足夠長度得到欲嵌入的聚焦波列，表4為嵌入的聚焦波參數。同理，分別研究嵌入點、嵌入聚焦波的歷時長度、幅值和譜峰周期對模擬波浪產生的影響。

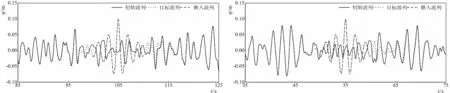
8-a 組次fc1 8-b 組次fc2

9-a 組次fc1、fc2 9-b 組次fc1、fc3

表4 嵌入聚焦波參數Tab.4 Embedded focusing wave parameters

圖8為嵌入聚焦波后各組次目標波列與初始波列的波面比較圖，從結果來看，其主要特點與嵌入規則波時類似，即嵌入聚焦波列后目標波列波形只在嵌入波列周圍發生變化。圖9為嵌入聚焦波后各組次目標波列與初始波列的波譜比較圖，表5為嵌入聚焦波后波列各統計參數變化表。從各組次對比結果來看，嵌入聚焦波時，其影響因素也與嵌入規則波時相似，即嵌入點、嵌入聚焦波的長度、幅值不會對模擬產生明顯的影響，而嵌入聚焦波的譜峰周期會對模擬波浪產生較大的影響。

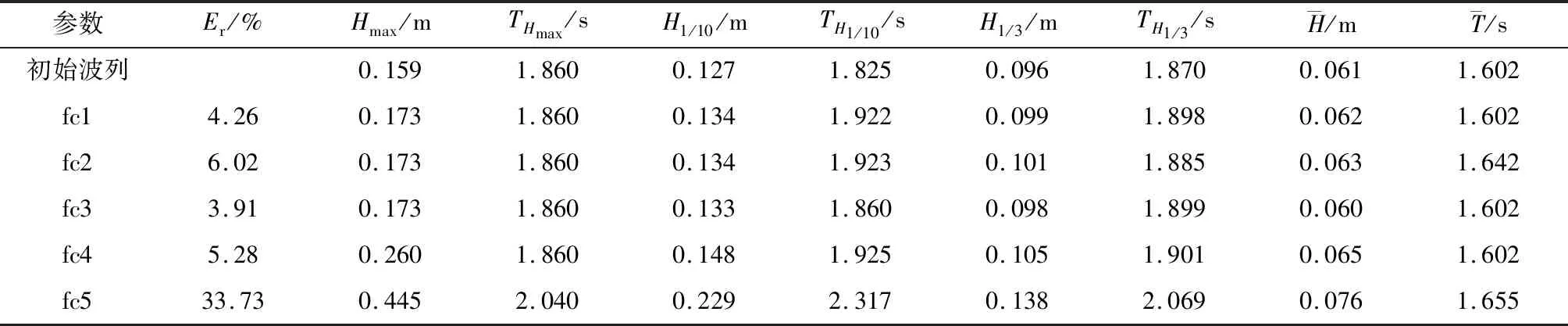
表5 嵌入聚焦波時初始波列和目標波列的統計參數表Tab.5 Statistical parameters of unconditional simulation and conditional simulation after embedding focusing waves

這里也可以看到與嵌入規則波不同的地方。從fc1和fc3組成結果的對比可以看到，聚焦波列的長度變大反而使得其統計參數和譜變化更小了，這是因為聚焦波列的長度越長，統計特性更加與初始波列趨于一致，初始波列產生的“排斥”因此就越小。從周期的影響上來看，聚焦波譜峰周期的變化比規則波周期的變化產生的影響更大，同樣的嵌入聚焦波的周期為1.5倍的初始波列有效周期，嵌入聚焦波時產生的特異波是嵌入規則波時的1.7倍。

3 結論

本文基于Borgman的條件波浪模擬理論，建立了相應的數值波浪模擬程序，可實現模擬生成既滿足某一特定波浪譜，又包含了某一特殊短波列的隨機波浪，并通過加入白噪聲的方式解決了計算中產生的數值不穩定問題。

嵌入波浪參數對于嵌入波浪后模擬波浪的影響研究結果表明，在進行條件波浪模擬時，嵌入波列的周期是主要影響因素，其與初始波列的有效周期越接近，則模擬效果越好，因此需要限定嵌入波列周期在一定區間范圍內。而在限定周期范圍內，嵌入點、嵌入波列的波高和長度的變化不會對模擬產生明顯的影響，但是如果嵌入波列的波高較大，嵌入波列后波浪的最大波高會增大。