單模腔場與Ξ 型三能級(jí)原子共振作用熵的糾纏演化

張 蕾

0 前言

原子與光場相互作用時(shí)反映場和原子的量子特性的非經(jīng)典效應(yīng)有很多，如：原子周期的崩塌-回復(fù)、壓縮態(tài)、反聚束效應(yīng)等，但這些效應(yīng)還不能完全說明其相互作用的動(dòng)力學(xué)的量子特征，自從Phoenix 和Knight[1-2]的量子熵理論提出以后，可以通過場熵或原子熵度量原子與光場相互作用時(shí)它們之間的糾纏特性，其結(jié)果是熵越大，糾纏程度越大，研究反映原子與光場關(guān)聯(lián)效應(yīng)的場（原子）熵已經(jīng)成為量子光學(xué)領(lǐng)域的一個(gè)熱點(diǎn)問題之一。近幾年，人們通過J-C 模型研究了原子與光場相互作用時(shí)系統(tǒng)原子熵以及場熵的演化特性，包括單光子、雙光子[3]和多光子[4]。李永平等研究了Ξ 型三能級(jí)原子與單模腔場在旋波近似下[5-6]系統(tǒng)場熵的演化，劉素梅研究了非旋波近似下光場與級(jí)聯(lián)型三能級(jí)原子相互作用系統(tǒng)場熵的演化[7]，張金芳等研究了運(yùn)動(dòng)級(jí)聯(lián)型三能級(jí)原子與單模場通過雙光子共振作用場（原子）熵的演化[8]，以及文獻(xiàn)[9]研究了單模腔場與Ξ 型三能級(jí)原子失諧作用熵的糾纏演化。本文基于一個(gè)Ξ 型三能級(jí)原子與單模腔場共振作用，分析和討論了原子初始狀態(tài)以及原子-腔場的耦合系數(shù)對(duì)該系統(tǒng)原子熵的影響。

1 理論及模型

圖1 給出了原子能級(jí)示意圖，|e〉、|f〉和|g〉分別是原子的第一、第二激發(fā)態(tài)和基態(tài)，能級(jí)|e〉和|g〉之間的躍遷是禁止的，|e〉與|f〉和|f〉與|g〉之間的躍遷與頻率為ω 的場共振，在J-C 模型中，描述一個(gè)三能級(jí)原子與一個(gè)單模腔場相互作用，在相互作用繪景中，哈密頓量可表示為[10]

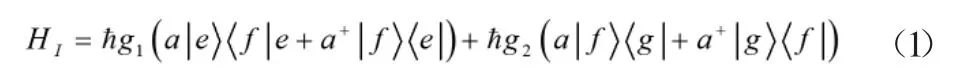
g1、g2分別表示|e〉→|f〉、|f〉→|g〉之間發(fā)生躍遷的耦合常數(shù)。a+和a 分別為光場的產(chǎn)生和湮滅算符，設(shè)任意時(shí)刻系統(tǒng)的態(tài)矢量為

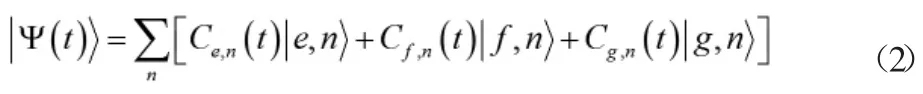
起初，原子處于基態(tài)和激發(fā)態(tài)的疊加態(tài)，光場為真空態(tài)，則初始時(shí)系統(tǒng)的態(tài)為

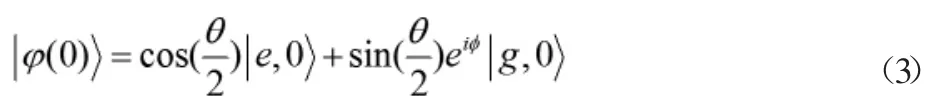
此后，系統(tǒng)態(tài)隨時(shí)間將演化為

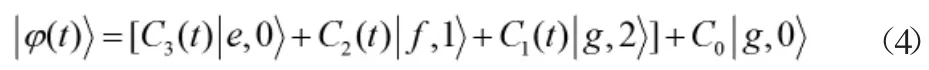
圖1 與單模腔場相互作用的三能級(jí)原子示意圖

態(tài)矢量的演化滿足薛定諤方程

根據(jù)（3）式，將（4）式代入（5）式可得出

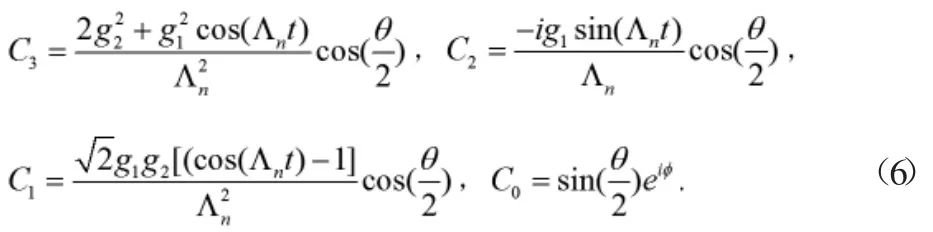
根據(jù)（4）式，可得原子的約化密度矩陣ρa(bǔ)（t）為

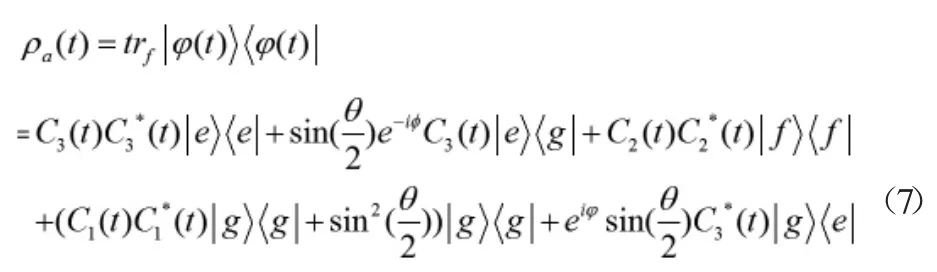
根據(jù)Araki-lieb 不等式[11]，對(duì)于任何t ＞0 的時(shí)刻，都有S=0，因而任意時(shí)刻光場系統(tǒng)的熵都等于原子系統(tǒng)的熵，根據(jù)（7）式，得到該系統(tǒng)的原子熵[12]：

式中λi（i=1，2，3）是原子約化密度矩陣的本征值，分別為

2 數(shù)值計(jì)算與數(shù)據(jù)分析

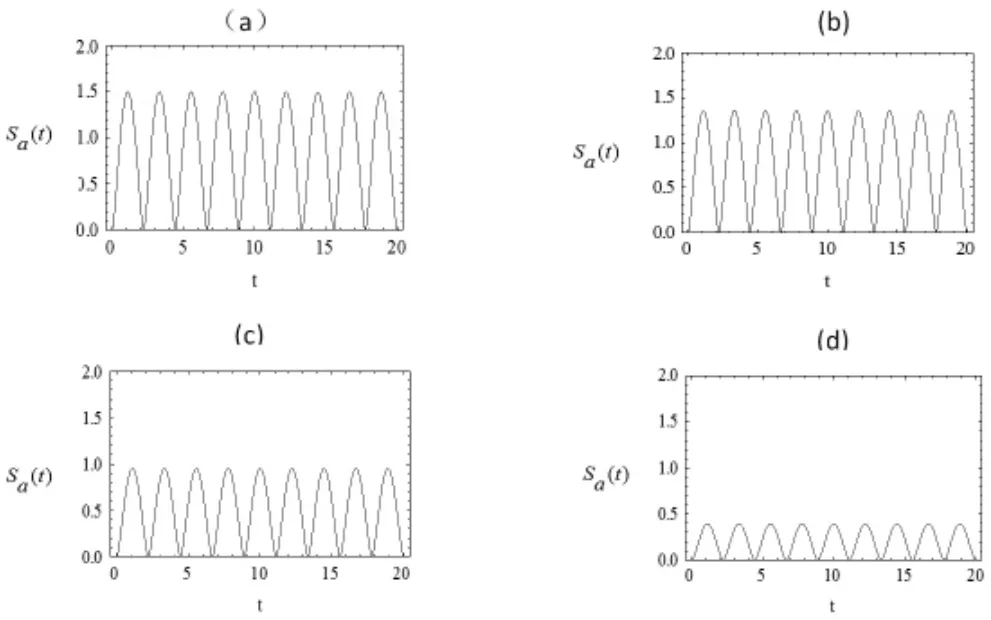
圖2

圖3

3 結(jié)論

本文研究了Ξ 型三能級(jí)原子與單模真空腔場發(fā)生共振作用時(shí)，原子初態(tài)以及原子-腔場的耦合系數(shù)對(duì)系統(tǒng)熵的影響，結(jié)果表明：（1）無論原子初始處于什么狀態(tài)，系統(tǒng)熵均隨時(shí)間周期性變化，隨著θ 值的增大，系統(tǒng)最大量子糾纏度在減小，但糾纏周期無明顯變化；（2）無論原子與光場兩種躍遷耦合常數(shù)之比k取何值，系統(tǒng)熵隨時(shí)間周期性變化，并且系統(tǒng)熵出現(xiàn)了雙峰現(xiàn)象，隨著k 值的增大，雙峰現(xiàn)象越加明顯并且它的周期和系統(tǒng)最大糾纏度明顯在減小.可以推斷，當(dāng)k 取合適值時(shí)，雙峰現(xiàn)象近乎消失。