Sim ulink 示例中小型微電網的簡化模型分析

萬卓鑫

1 模擬過程簡述[1]

從20 h 到4 h，太陽能發電量為0 W；從14 h 到15 h 達到峰值（5 kW）。電力負荷作為普通住宅的典型負荷變化，分別在9 h（6500 W）、19 h、22 h（7 500 W）達到峰值。從0 h 到12 h，從18 h到24 h，由電池控制器進行電池控制。電池控制對電流進行跟蹤控制，使從三繞組變壓器二次側流入系統電源的有功功率設置為0。此時，三繞組變壓器二次側的有功功率始終在零附近。蓄電池在微網供電不足時提供不足的電流，當微網供電超過負荷時從微網吸收多余的電流。從12 h 到18 h，不進行電池控制。蓄電池荷電狀態（SOC）固定在一個常數上，并且自蓄電池充放電后不發生變化，電池不是由電池控制器執行的。在8 h 時，普通住宅3 號負荷被斷路器斷開10 秒。

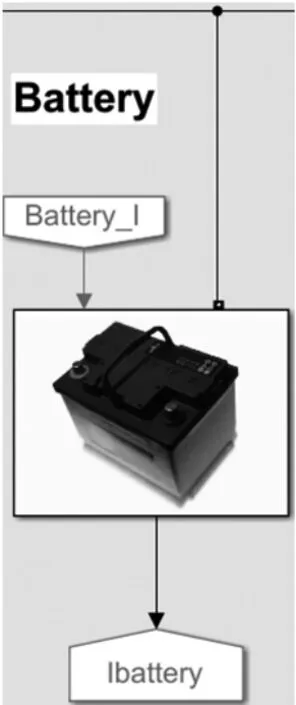
圖1 蓄電池模塊

2 模型組成結構和原理分析

該微電網的基本組成由一個電力網絡，一個太陽能發電系統，一個蓄電池，以及三個普通住宅的典型負荷，構成簡化的微網模型。其中包含有對太陽能、蓄電池的控制模塊，以及Scopes（示波器）模塊等。

2.1 蓄電池及其控制模塊

2.1.1 蓄電池模塊簡述

蓄電池通過可控交流電流源并聯阻尼器來模擬，輸出連接在微網變壓器二次側。如圖1 所示，Battery_I 輸入端口輸入的是通過對變壓器二次側電壓電流進行跟蹤控制，得到的電流作為蓄電池中的可控電流源的輸入。Ibattery 輸出端的From 在整個模型的示波器（Scopes）部分里。Scopes 模塊會在后面的示波器模塊分析中進行分析。

2.1.2 蓄電池控制模塊

如圖2 可以看出，蓄電池控制模塊對變壓器的二次側電壓電流采樣作為輸入，根據控制要求，從0 h 到12 h，和從18 h 到24 h，由電池控制器進行控制；從12 h 到18 h，不進行電池控制。所以還有一個控制輸入信號，此控制輸入信號的輸入在Scenario 模塊中，在12 h 到18 h 期間Control 信號輸出為0。

當來的控制信號為0 時，使從變壓器二次側流入系統電源的有功功率在從0 h 到12 h，和從18 h 到24 h 的時間段內保持為0。這時候輸出I_RMS 作為發給蓄電池的充放電電流。因此使在0 h 到12 h，和從18 h 到24 h 的時間段內由蓄電池供電給普通住宅負荷。同理在從12 h 到18 h 時，不進行電池控制，I_RMS輸出為0，這段時間不由蓄電池發電。在圖2 的后半段，可以看出取I_RMS 為電流有效值，與變壓器二次側的電壓的相位組成復數電流值，乘上轉換為輸出給蓄電池的電流。

圖2 中還可以看到還有一個Battery_Simple_Dynamics 模塊，此模塊用于計算所消耗的蓄電池的電能，以及蓄電池的SOC。其內部結構如圖5 所示，它的電池容量值（Capacity）AH 設置為1 000 Ah。

計算其電能消耗所用公式[3]為：

圖3 Battery_Simple_Dynamics 模塊內部

該公式的I，為模型中的I_RMS，即為上述的蓄電池控制模塊所輸出的蓄電池的充放電電流。所消耗電能就是該電流在時間區域內的積分。

蓄電池的SOC 的計算所用公式[2]為：

該公式的QN為標稱容量，在這里是之前所設置的電池容量值1 000 Ah；其中的I 為模型中的I_RMS；其中的η 為充放電效率，在這個模型里設至為了1。

在計算SOC 時，Integrator 模塊的初始條件設置為AH×0.2×3 600，也就是說在t0時Integrator 模塊輸出為AH×0.2×3600，因此可以看出此模型是使Battery_SOC 的初值為80%

2.2 光伏及其控制模塊

2.2.1 太陽能電池板模型簡述

如圖4，為太陽能電池板模型，太陽能電池板也是通過可控電流源并聯阻尼器來模擬。通過圖4 可以看出有一個輸入電流PV_I 與一個局部陰影模塊（Partial Shading）相乘構成了太陽能電池板的輸入；其輸出端Ipv 連接到了Scopes 模塊中，整個太陽能電池板連接在電網上為負荷供能。

2.2.2 太陽能電池板控制模塊分析

輸出電流PV-I 是通過圖5 的模塊得到：左側時鐘輸入一個模擬時間信號，下面那條分支為太陽能查找表模塊（Solar Data 1-D Lookup Table），這是通過事先的設置出來的太陽能電池板的輸出功率，可人為修改。可以發現從20 h 到4 h，太陽能發電量為0 w；從14 h 到15 h 達到峰值。后面的除以200 再乘上變為峰值，與網二次側的電壓的相角結合得到復數電流PV-I 提供給太陽能電池板。

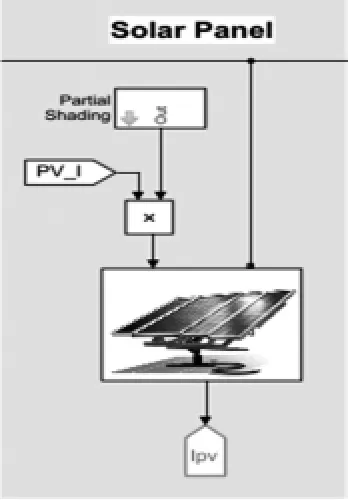
圖4 太陽能電池板

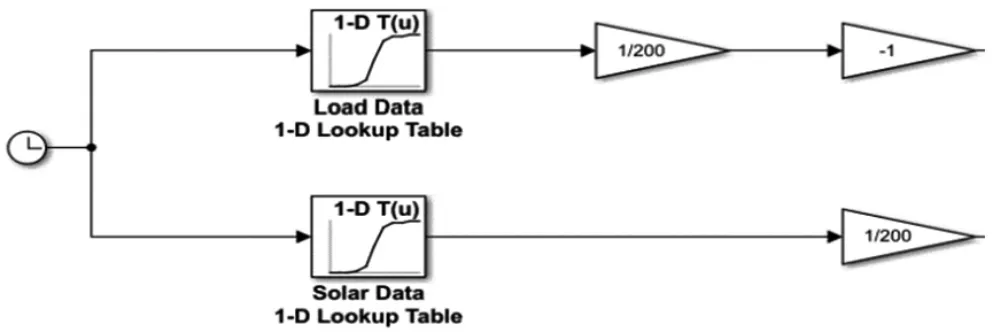
圖5 Scenario 模塊

然后分析在太陽能電池板上Partial Shading 模塊，通過設置Ton 和Toff 的值確定在哪段時間內太陽能電池板上出現陰影區域，這里設置出現陰影的時間為11 h，持續時間為20 s。其中Factor 設置值為0.3，太陽能不能完全發揮作用，控制電流變成了原來的30%；其他時間輸出為1。

2.3 電力負荷及其控制模塊

2.3.1 電力負荷模型簡述

電力負荷在此模型中使用是三個普通住宅，內部結構都相同。這里的電力負荷也是通過可控交流電流源并聯阻尼器來模擬，只是多了一個串聯電阻。其中的Load3_I 的輸入是來自于整個模型中的Scenario 模塊。其中的IL3 是連接到了Scopes模塊中了。

此處的3 號普通住房連接電網側有一個MainBreaker，通過Trip Signal 給出控制信號，Trip Signal 的設置的斷路器斷開時間在8h 時，斷開持續時間為10s，這期間，3 號普通住房負荷與電源端脫離，不再接收能量。

2.3.2 電力負荷的控制方案

電力負荷的控制和太陽能電池板的控制是在此模型的同一個模塊Scenario 中，因此分析方法相同，這里做簡要說明。如上圖圖6 中，按時鐘通過Load Data 1-D Lookup Table，經運算得出負荷消耗電流有效值的曲線。把得出的電流分給三個負載，總的負荷消耗功率在9 h 達到一個峰值6500 W，在19 h、22 h 達到一個峰值7500 W。

2.4 電網側模塊連接分析

該微網模型的網側連接模型從左到右依次是電網模型、變壓器、輸電線路、星型連接的RLC 負載以及一個三繞組變壓器。電網模型電壓幅值為66 kv，A 相相角為0°；變壓器的二次側電壓為6.6 kV；SEND1 模塊，是一個π 型等值電路[4]，長度為1 km。后面的變壓器使電壓變為了有效值為200 V 的電壓。

3 Scopes模塊分析

通過以下的分析，可對一天里各種供電源以及負荷的工作狀態有一個較為清晰的認識。

首先我們看第一個波形圖圖6 太陽能電池板發電量隨時間變化規律。

通過上圖，知太陽能電池板在4 h 到20 h 期間工作；還可看見在14 h 到15 h 期間，太陽能電池板輸出功率達到峰值5 kW。在11 h 到11 h20 s，由于陰影遮擋，太陽能電池板提供給負荷的功率變為了原先的30%，如圖中一個下降的尖峰。

接著分析同在Scenario 模塊中設置的三個普通住宅，也就是負載需求功率隨時間的變化規律，如圖7 所示，在0 h 時負載需求的功率約為3 280 W；在大概1 h 到6 h 這個時間段，負荷的需求功率較低，一段時間內只保持基本需求功率。6 h 后負荷需求開始上升；在8 h 到8 h10 s 時，3 號負荷被斷路器切掉，在圖中有一個持續10 s 的尖峰。6 h 上升到大概在9 h 時，負荷的需求開始降低；到晚上的17 h 左右，負荷需求增大直到約22 h時，符合日常的用電規律。

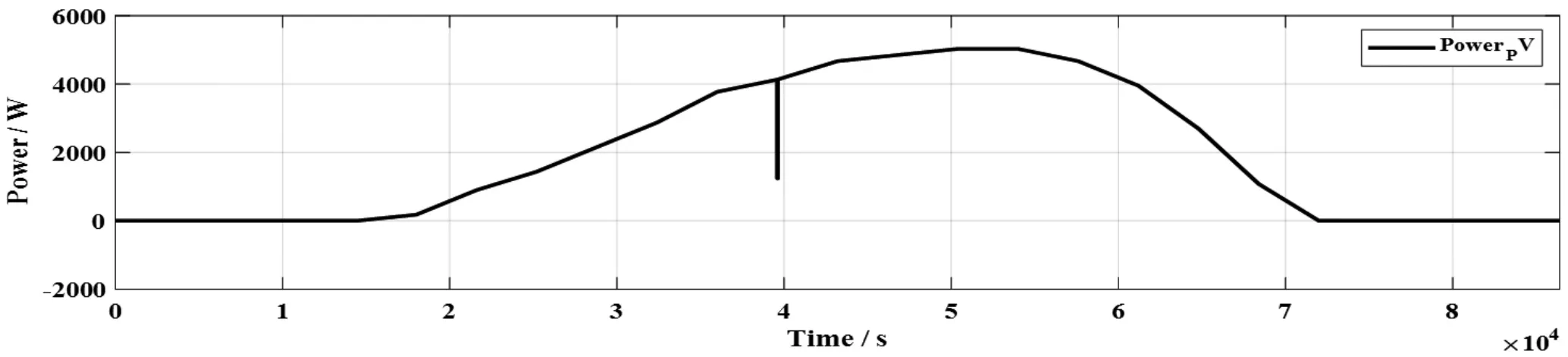
圖6 太陽能電池板發電量隨時間變化規律

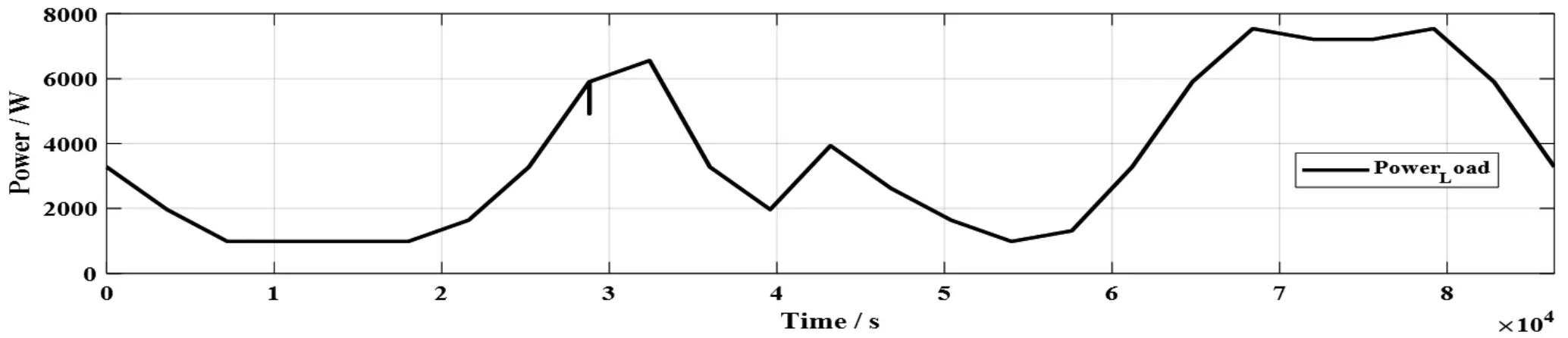
圖7 負載功率隨時間變化規律

圖8 三繞組變壓器二次側功率隨時間變化規律

然后分析三繞組變壓器二次側功率隨時間變化規律。如下圖8 所示。因8 h 時3 號負載斷開，因此有一個擾動；在11 h 時的太陽能電池板被陰影遮擋，所以也有一個擾動。可以注意到圖中12 h 到17 h 左右時，電網提供的功率為正值，也就是說太陽能電池板提供的功率過剩，送到了電網；而17 h 左右到18 h時，太陽能電池板不足以單獨為負荷提供功率，所以由電網為負荷提供一部分。18 h 后蓄電池投入，變壓器二次側功率回升為0 W。

然后分析蓄電池輸出的功率隨時間變化的規律。如圖9 所示，在8 h 時，由于掉負荷，發出的功率減小，有一個尖峰。在10 h 到12 h 時，蓄電池輸出的功率為負值，太陽能電池板發電把多余的能量給蓄電池存儲；在其間的11 h 到11 h20 s 時，尖峰是為了填補太陽能電池板由于陰影遮擋使供給負荷功率不足的那一部分。

由以上分析可總結出，在各部分的功率供需滿足一個關系。

太陽能輸出功率+蓄電池輸出功率-電網輸出功率=負荷輸出功率 （3）

公式中的太陽能與蓄電池的輸出功率取正，輸入取負；電網在圖中為正值時是給電網輸入功率，為負時是輸出功率，所以上式為減去電網輸出功率。

接下來簡要分析一下蓄電池的SOC 值隨時間的變化規律，如下圖10 所示。

該模型主要是靠蓄電池和太陽能供電，所以蓄電池一般不會處在浮充或者滿電狀態，因此初值設置為了80%[3]。從0 h 到10 h 左右時，SOC 一直處于下降狀態，當在10 h 到12 h 時SOC有一個較小的回升，是由于太陽能電池板發電把多余的能量提供給了蓄電池存儲。在12 h 到18 h 時，蓄電池切出，SOC 值維持在了72.85%左右，在18 h 后又開始投入，為負荷供電。

圖9 蓄電池功率隨時間變化規律

圖10 SOC 隨時間變化規律

4 模型搭建注意事項

（1）搭建模型時要對各個模塊進行注釋，以便更好理解模型。盡量對相同功能的模型搭建放在一個模塊中。

（2）注意仿真的客觀性，要與實際情況相符合，不能脫離實際，如設置負荷需求功率時，在凌晨時需求最少，晚上時需求最多，這些是符合典型情況的。

（3）搭建模型應該具有靈活性，清楚自己的目的是什么，不要把問題弄復雜，如太陽能電池板、蓄電池、電力負荷內部結構基本一致，從而簡化了模型。