馬斯京根法在錦屏二級水電站減水河段洪水演算中的應用研究
侯國棟,羅 浩
(1.中國電建集團成都勘測設計研究院有限公司,四川 成都 610072;2.雅礱江流域水電開發有限公司,四川 成都 610051)
1 工程概況
錦屏二級水電站位于四川省涼山彝族自治州木里、鹽源、冕寧三縣交界處的雅礱江干流錦屏大河灣上,采用“截彎取值”的引水發電系統。錦屏二級水電站減水河段西起貓貓灘閘址,東至大水溝廠房,河段長約123 km,沿途有磨子溝、子耳溝、九龍河、朵落溝、蘿卜絲溝等多條支流匯入。
研究河段內已建有2個水文站和15個水位站,水文站已有10多年的水文資料,水位站收集了近3年的水位數據。本文主要是根據已知數據,演算下游15個水位站的流量變化過程。
2 馬斯京根法的基本原理和演算參數的確定
洪水演算是根據河道已知斷面的洪水過程來推求下游某斷面洪水變化過程的一種方法,分為流量演算和水位演算兩種。河道流量演算是以圣維南方程組為理論基礎,利用上斷面流量演算下游斷面的流量變化過程。目前常用的河道流量演算方法大致可分為水文學和水力學兩類方法。水力學法需要求解圣維南方程組,計算過程繁雜且易出錯,而水文學法中的馬斯京根法由于計算過程簡單,演算精度高、對河道資料要求相對較低,在實際生產過程中,應用最為廣泛。
2.1 馬斯京根法的基本原理
將馬斯京根槽蓄方程與水量平衡方程聯解,可以得到馬斯京根演算基本公式:
Q2=C0I2+C1I1+C2Q1
(1)
其中
(2)
C0+C1+C2=1
(3)
式中,I、Q為河段入流、出流;腳碼1、2表示時段初、末時刻。C0、C1、C2是馬斯京根法參數K和x的函數。
對于一個河段,只要確定了馬斯京根參數K、x的值以及演算時段后,便可以求出C0、C1、C2的值,根據入流斷面流量變化過程I(t)及下斷面起始流量值計算出下斷面的流量過程Q(t)。
錦屏二級水電站減水河段約123 km,洪水傳播時間較長,為了簡化計算過程,計算時段Δt取值為0.5 h,為了使計算結果更大程度反映真實的洪水變化過程,本文采用馬斯京根分段流量演算法進行洪水演算,即:將演算河段劃分為n個單元河段,用馬斯京根法連續進行n次演算,以求得出流過程。也就是說,馬斯京根分段流量演算法的計算需要確定每一個分段的參數K1、x1以及分段個數n的值。
2.2 參數K、Δt的取值
K值是槽蓄曲線的坡度,也就是蓄量常數,等于在相應蓄量W下恒定流狀態的河段傳播時間。很顯然,K值隨恒定流的流量大小而變化。
根據錦屏二級減水河段各水位站的水位資料和錦屏水力發電廠提供的錦屏閘壩出流數據,可以計算出不同流量級洪水到達下游各斷面的傳播時間,從而求得K值。令Kl=Δt=0.5 h,可以求得各水位站洪水分段演算的次數n的值。
(4)
2.3 參數x1值的確定
參數x反映了河槽的調蓄作用大小,為流量比重系數;與河道、洪水各個參數有關,隨著河道洪水參數的變化而變化。x的變化規律為:當0≤x≤0.5時,x越小,表明河槽的調蓄作用越大。同一條河流,上游的x比下游的x大。
假設水面為直線,根據水文預報基本原理得到:
(5)
式中,l為特征河長;L為計算河段的長度。其中,河段長度L可以根據河段流域地圖查詢得出。
由水文預報特征河長相關知識可知,特征河長I的計算公式為:
(6)
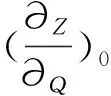
根據(4)式和(5)式可得,
(7)
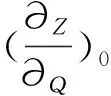
3 實例應用及誤差分析
本文以錦屏二級閘壩下游7 km的大沱崗亭站作為上游已知斷面,推求下游九龍河口水位站斷面的流量變化過程,進而闡述本方法在實際洪水演算中的應用。
九龍河口站位于大沱崗亭站下游約29 km處,計算河段區間內有多條支流匯入,但支流匯入流量較小、流量占比基本可忽略不計,因此本文忽略區間支流匯入的流量。
3.1 參數計算及演算過程
本文以錦屏二級減水河段2017年8月14日至15日的洪水場次為例,以大沱崗亭站為已知上游斷面,演算九龍河口站斷面的流量變化過程。
表1為運用馬斯京根法分段演算洪水的計算過程,其中表內第2列為大沱崗亭站的流量變化過程,第12~14列為分段演算的流量結果。根據已有的資料可以推算出,大沱崗亭站500 m3/s的洪水波傳輸至九龍河口站大約需要3 h,則九龍河口站的分段次數n為6,即表1中第14列即為九龍河口站演算的流量結果。
3.2 洪水演算成果對比分析
本文分別選取了減水河段500 m3/s、1 000 m3/s、2 000 m3/s、3 500 m3/s等4個流量級洪水場次的洪水過程,運用馬斯京根分段流量演算法分別計算出了下游九龍河口站的流量。圖1~4為各流量級洪水演算的流量成果與實際斷面流量變化過程對比。
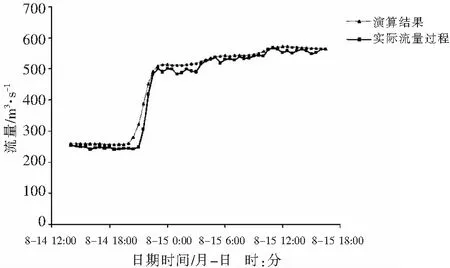
圖1 500 m3/s流量級洪水演算成果與實際流量對比示意
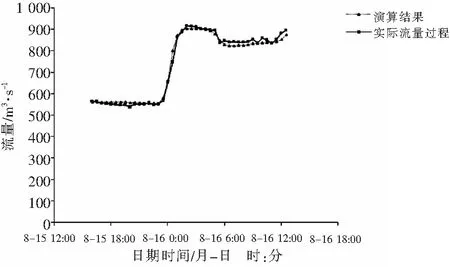
圖2 1 000 m3/s流量級洪水演算成果與實際流量對比示意
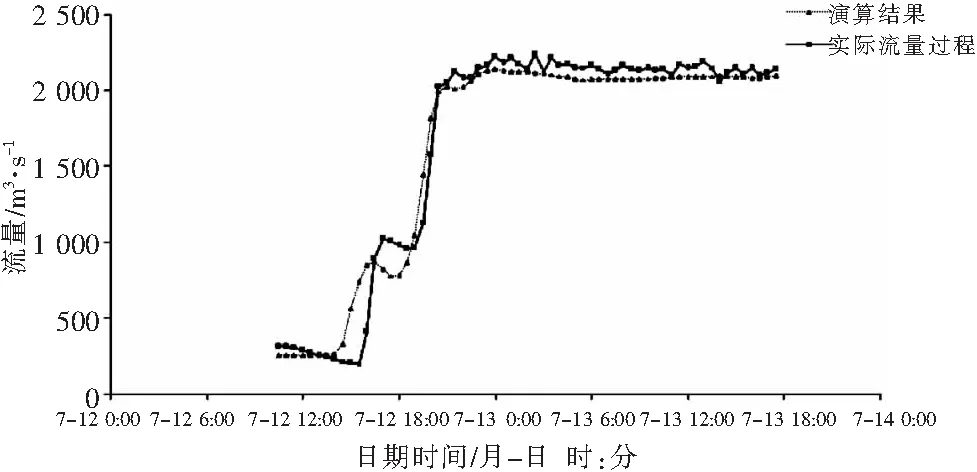
圖3 2 000 m3/s流量級洪水演算成果與實際流量對比示意
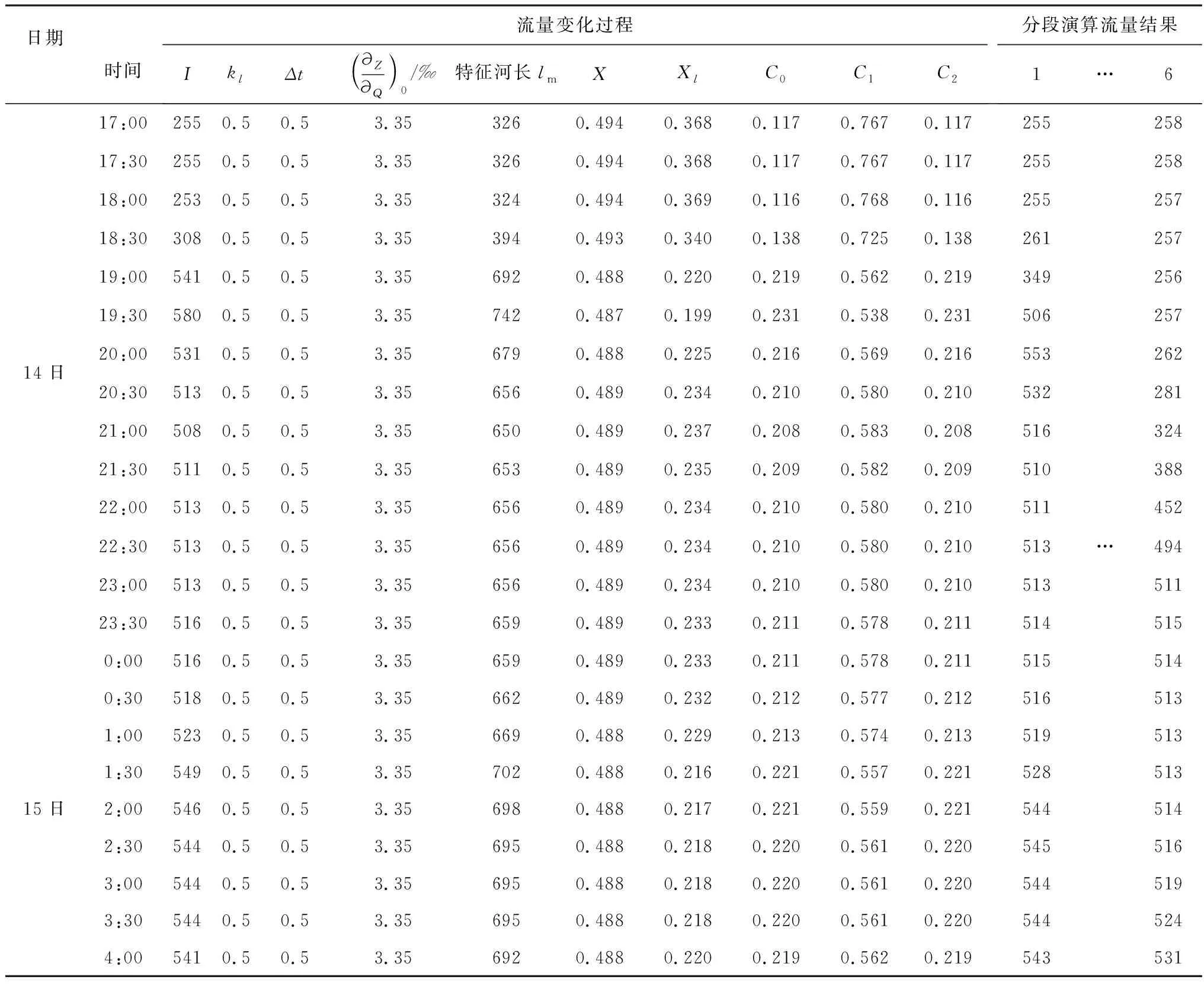
表1 馬斯京根分段演算法500 m3/s流量級洪水演算過程
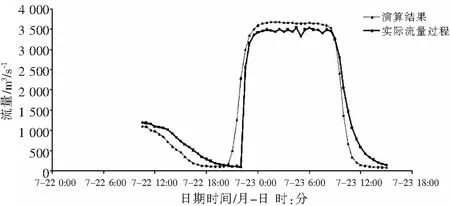
圖4 3 500 m3/s流量級洪水演算成果與實際流量對比
由圖1~4可以看出,馬斯京根分段流量法演算的流量成果基本與實際流量變化過程相符,洪峰達到時間較為接近。但2 000 m3/s和3 500 m3/s流量級洪水漲落水前后的低水部分演算結果誤差較大,這是由于洪水分段演算時,未能根據分段演算的次數而改變相應的計算參數,從而降低了部分演算成果的精度。
4 結 語
(1)通過本文實例可以看出,根據馬斯京根法參數的定義和代表的含義來直接求值演算參數的方法,可以避免試算法過程繁瑣和摻雜人為因素的困難,具有使用簡單、演算精度高、適應性強等特點。
(2)在使用本方法時應根據相關條件的變化及時更新演算參數,避免參數取值不當而引起誤差,可以通過軟件編程來實現參數自適應演算模型。

