網(wǎng)格化GNSS弱干擾源定位方法

劉睿,陳奇東,甄衛(wèi)民

(中國電波傳播研究所,山東 青島 266107)

0 引 言

全球衛(wèi)星導(dǎo)航系統(tǒng)(GNSS)為導(dǎo)航帶來了革命性的變化,它在全球范圍內(nèi)為無限多的海陸空天用戶提供精確的實(shí)時位置、速度和時間信息,一旦GNSS受到干擾,就會對與國家安全、國民經(jīng)濟(jì)等方面密切相關(guān)的關(guān)鍵基礎(chǔ)設(shè)施造成嚴(yán)重影響和不可預(yù)計的后果[1]. GNSS信號落地功率低,約為-13 dBm,同時信號采用擴(kuò)頻體制,其功率譜密度更低,頻譜嚴(yán)重地淹沒在環(huán)境噪聲當(dāng)中,很弱的干擾即可影響GNSS的應(yīng)用[2].

常用的網(wǎng)格化GNSS干擾源定位方法有波達(dá)方向(DOA)定位方法[3],到達(dá)時間差(TDOA)定位方法[4]和到達(dá)信號強(qiáng)度(RSS)定位方法[5]. 其中TDOA方法以其定位速度快、精度高等特點(diǎn)獲得了廣泛的推廣應(yīng)用. 目前TDOA通常使用廣義互相關(guān)算法(GCC)[6]等方法估計接收機(jī)間的信號到達(dá)時差,然后通過雙曲線定位算法解算干擾源位置.

對GNSS弱干擾源定位時,上述方法對信噪比低的情況適應(yīng)能力較差,針對該問題,本文提出一種基于信號噪聲分離的差方均值函數(shù)擬合(MFDSS[2])的網(wǎng)格化GNSS弱干擾源定位方法,方法采用MFDSS方法實(shí)現(xiàn)時差估計,然后利用Chan[7]雙曲線定位算法解算干擾源位置. 同時,本文還介紹了采用上述方法的網(wǎng)格化GNSS弱干擾源定位系統(tǒng)組成,對系統(tǒng)的定位性能進(jìn)行了仿真與分析并給出結(jié)論.

1 網(wǎng)格化GNSS弱干擾源定位系統(tǒng)及接收信號模型

網(wǎng)格化GNSS弱干擾源定位系統(tǒng)的組成框圖如圖1所示,包含監(jiān)測接收層、數(shù)據(jù)傳輸層和中心處理層三個層次. 監(jiān)測接收層由網(wǎng)格化監(jiān)測接收機(jī)組成,實(shí)現(xiàn)對干擾信號的采集接收并對接收數(shù)據(jù)打時間標(biāo)記;數(shù)據(jù)傳輸層由4G等無線通信鏈路實(shí)現(xiàn);中心處理層的數(shù)據(jù)處理平臺收集各接收機(jī)數(shù)據(jù),通過執(zhí)行本文方法實(shí)現(xiàn)對弱干擾信號的準(zhǔn)確定位.

圖1 網(wǎng)格化GNSS弱干擾源定位系統(tǒng)的組成框圖

存在干擾的情況下,監(jiān)測接收機(jī)接收到的信號包含目標(biāo)干擾信號s(n)和噪聲信號n(n),接收機(jī)接收信號模型如式(1),對于目標(biāo)干擾信號的檢測定位,噪聲信號n(n)包含隱藏在噪聲下的GNSS信號,具有相關(guān)性,對時差估計有一定影響.

x(n)=s(n)+n(n).

(1)

2 基于MFDSS的弱干擾源定位方法

2.1 基于MFDSS的時差估計方法

方法利用目標(biāo)干擾信號與噪聲間的正交性采用奇異值差分譜濾除噪聲,然后通過擬合方法求出差方均值函數(shù)精確的極小值以實(shí)現(xiàn)弱干擾的時差估計值.

2.1.1 奇異值差分譜噪聲濾除方法

方法首先依據(jù)式(1)對接收信號構(gòu)造Hankel矩陣,x(n)信號長度為N,x(n)的Hankel矩陣表達(dá)式如下:

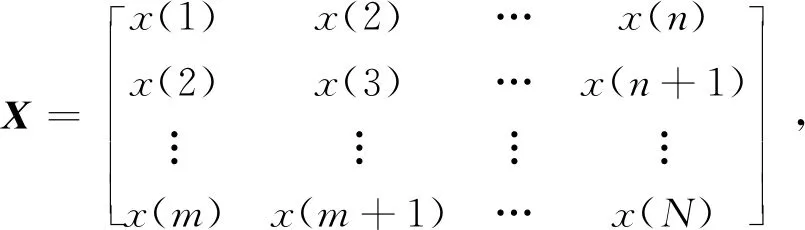
(2)

式中,根據(jù)N為偶數(shù)和奇數(shù)時,m取值分別為N/2和(N+1)/2，n取值分別為N/2+1和(N+1)/2.對矩陣X進(jìn)行奇異值分解可得式(3):

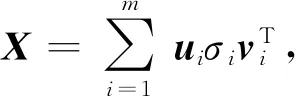
(3)

式中：ui為m維列向量；σi為矩陣X的奇異值；vi為n維列向量,分解后σi由大到小排列并利用式(4)構(gòu)造奇異值差分譜b=(b1,b2,…,bm-1),其中bi的表達(dá)式為

bi=σi-σi+1,i=1,2,…，m-1.

(4)

方法通過查找差分譜b最大值bk,利用前k個奇異值重構(gòu)Hankel矩陣,表達(dá)式如下:

(5)

2.1.2 差方均值函數(shù)擬合時差估計方法

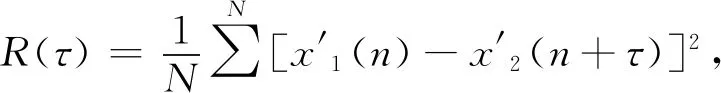
(6)

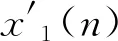
(7)

其中,τm=arg minτ(R(τ)).

2.2 Chan定位方法

Chan定位算法本質(zhì)上是雙曲線定位方法,雙曲線定位示意圖如圖2所示,通過估計干擾源到兩接收機(jī)時差可以列出雙曲線方程,多個雙曲線交匯可確定干擾源位置. 完成時差估計后可列雙曲線方程如下:

ri,1=cDi=ri-r1,i=2,3,…,N，

(8)

(9)

圖2 雙曲線定位示意圖

Chan算法在成高斯分布的時差估計誤差下定位效果好,因此較好地適用于本文的應(yīng)用場景[8]. 方法進(jìn)行兩次加權(quán)最小二乘(WLS)以實(shí)現(xiàn)雙曲線方程的精確求解,通常場景下,雙曲線方程冗余,式(9)可寫成如下矩陣形式,表達(dá)式如下:

Gaza=h,

(10)

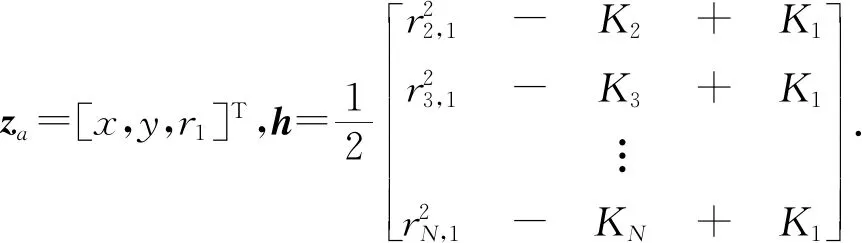
ψ=h-Gaza0，

(11)

式中,za0為無噪聲時za值. 依據(jù)文獻(xiàn)[9-10]可給出式(11)的WLS解,表達(dá)式如下:

(12)

利用式(12)得出的解可構(gòu)造新的方程組進(jìn)行第二次WLS以改善目標(biāo)干擾源位置的估計結(jié)果,方程組表達(dá)式如下:

(13)

3 仿真分析

仿真模擬真實(shí)GNSS弱干擾源網(wǎng)格化定位的應(yīng)用場景,對比統(tǒng)計本文方法和最為常用的基于GCC的TDOA定位方法的定位精度. 仿真過程中,目標(biāo)干擾信號s(n)功率設(shè)置為-125 dBm,為帶寬2.046 MHz的弱干擾信號,添加噪聲信號n(n)后目標(biāo)干擾信號的信噪比(SNR)為-7 dB,目標(biāo)信號淹沒在噪聲下,其中n(n)包含功率為-128 dBm的GNSS信號. 信號載頻為1575.42 MHz,采樣頻率為16.368 MHz.

文獻(xiàn)[1]建議實(shí)際布設(shè)網(wǎng)格化監(jiān)測接收機(jī)時,為提升定位效果,需在網(wǎng)絡(luò)幾何中心設(shè)置基準(zhǔn)接收機(jī). 圖3示出仿真接收機(jī)布局及干擾源位置,分別仿真典型四接收機(jī)和七接收機(jī)布局方式下的定位效果,接收機(jī)布設(shè)在半徑1.5 km的圓上,中心布設(shè)基準(zhǔn)站. 干擾源坐標(biāo)為(300,500),仿真考慮20 ns的時間同步誤差.

圖3 仿真接收機(jī)布局及干擾源位置

圖4為某次定位處理的奇異值差分譜噪聲濾除效果圖,其中圖4(a)為目標(biāo)干擾信號采樣波形,圖4(b)為目標(biāo)干擾信號混入噪聲信號波形,圖4(c)為奇異值差分譜噪聲濾除后波形.圖4表明本文方法可以很好地實(shí)現(xiàn)噪聲濾除,從而提升弱干擾信號的時差估計效果.

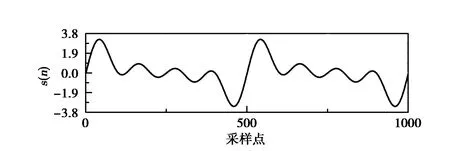
(a)目標(biāo)干擾信號

(b)目標(biāo)干擾信號+噪聲信號

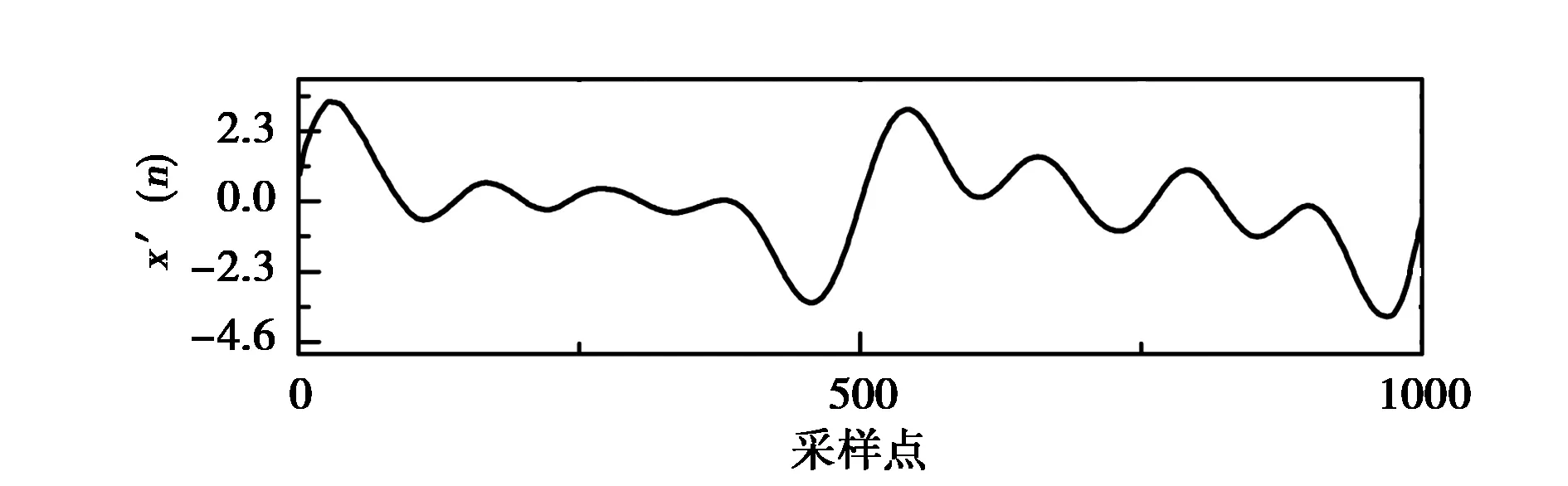
(c)噪聲濾除結(jié)果圖4 奇異值差分譜噪聲濾除效果

在上文仿真條件下進(jìn)行200次定位試驗,并對定位結(jié)果進(jìn)行統(tǒng)計. 圖5～6分別示出四接收機(jī)、七接收機(jī)本文方法和GCC方法定位效果對比,相對于GCC方法，本文方法定位結(jié)果更接近于真實(shí)干擾源位置. 對上述場景下不同定位方法的均方根誤差(RMSE)進(jìn)行統(tǒng)計,統(tǒng)計結(jié)果如表1所示. 在四接收機(jī)情況下,本文方法相比于GCC方法,定位RMSE由70.05 m提升至24.30 m;在七接收機(jī)情況下,本文方法相比于GCC方法,定位RMSE由25.92 m提升至7.67 m. 仿真結(jié)果表明在弱GNSS干擾定位的場景下,本文方法較好地改善了噪聲和導(dǎo)航信號對干擾源定位效果的影響,提升了定位精度.

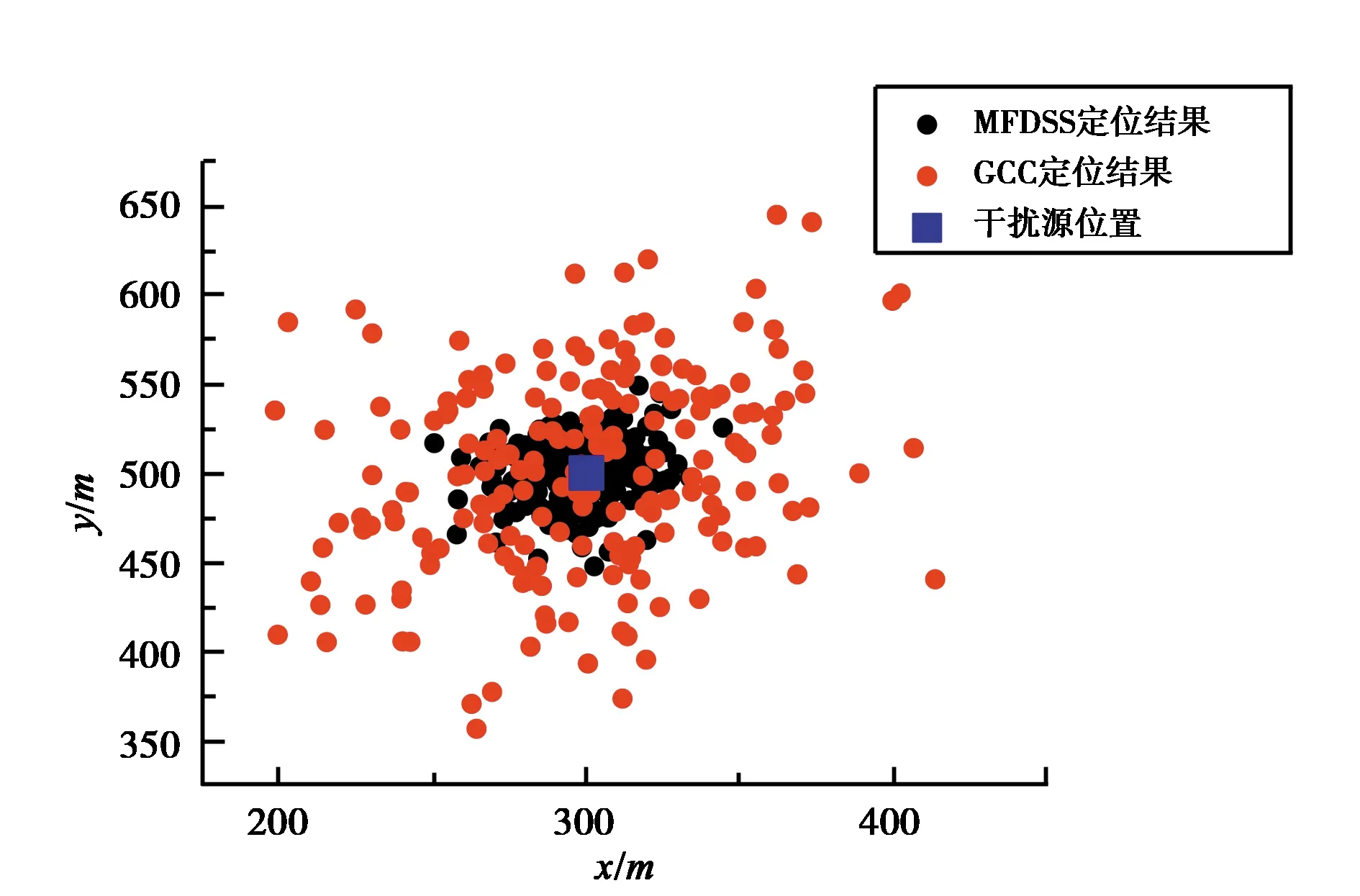
圖5 四接收機(jī)定位效果

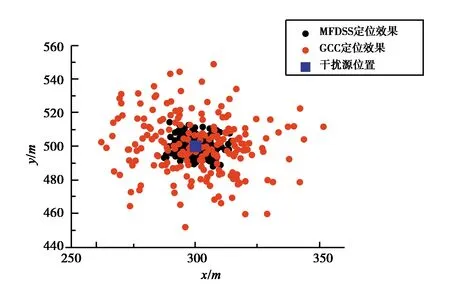
圖6 七接收機(jī)定位效果

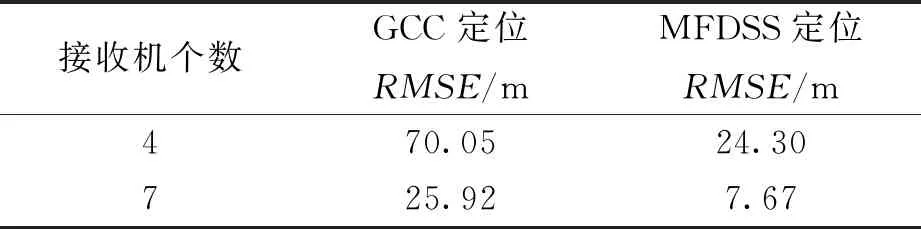
表1 不同場景下的定位RMSE統(tǒng)計

4 結(jié)束語

本文介紹了網(wǎng)格化GNSS弱干擾源定位的系統(tǒng)組成,分析了現(xiàn)有方法在該應(yīng)用場景下尚存的問題,針對這些問題提出了一種基于MFDSS的網(wǎng)格化GNSS弱干擾源定位方法. 文章詳細(xì)描述了該方法的原理,并針對弱GNSS干擾定位的應(yīng)用場景和典型接收機(jī)布局方式,對比仿真了本文方法和基于GCC的TDOA算法的定位效果. 仿真結(jié)果表明該場景下本文方法相對于目前常用的網(wǎng)格化定位方法,定位效果提升明顯.