整車道路耐久性試驗規范模塊化研究與應用
程佳勇 陳黎君


摘 要:整車道路耐久性試驗周期較長,試驗規范內容多,并且各規范包含的子規范種類多,數量龐大。子規范排布順序不合理,會產生過多的無效里程,拉長開發周期。本文對試驗規范模塊化進行研究分析,以提高試驗效率,縮短試驗周期 ,結果表明整車道路耐久性試驗效率得到提高,周期縮短。
關鍵詞:道路耐久性試驗 規范 蟻群算法 模塊化
1 引言
整車道路耐久性試驗是車輛在上市前對整車各項指標評估的最后一道檢驗,整車道路耐久性試驗周期長短直接影響到整車開發周期。而整車道路耐久性試驗規范內容多,每個規范包含多條子規范,不同的子規范執行場地多樣且復雜,并且子規范不得連續重復執行,再加上腐蝕子規范對時間間隔與天氣有特殊要求,如果子規范的排布不合理,會產生過多的無效里程、拉長開發周期、零件損傷超考核等一系列問題。因此,合理布局規范排布,對整車道路耐久性試驗至關重要。
本文對規范模塊化進行研究分析,達到提高效率,縮短驗證周期的目的。
2 整車道路耐久性試驗簡介
整車道路耐久性試驗規范內容是通過客戶使用測評團隊收集客戶在實際使用中的數據,結合試車場的道路采集數據來制定規范及規范循環數[1]。整車道路耐久性試驗規范是由多個子規范組合而成,每個子規范是一個獨立的測試任務。試車場用于耐久性測試的道路主要包括:高速路、石塊路、搖擺路、扭曲路、比利時路、破損路、坑洞、城市模擬路、坡道等,根據這些不同道路工況,調整循環數,對整車耐久性能進行考核。整車道路耐久性認證試驗里程達4萬公里。子規范模塊化是指將多個子規范按照均勻分布、限制重復個數、時間間隔、里程等因素進行封裝。
3 蟻群算法介紹
蟻群算法是由Dorigo.M等在20世紀90年代初提出的一種新型進化算法,它源于對螞蟻搜索問題的研究。蟻群算法由于具有啟發性、并行性、強魯棒性等特點,對復雜問題的適應性較強,因而被廣泛應用于旅行商問題[2]、路徑規劃問題[3-4]等。
以路徑規劃為前提,對蟻群算法分析。初始時刻,只螞蟻隨機放置于城市中,各條路徑上的信息素初始值相等,設:為信息素初始值,可設,是由最近鄰啟發式方法構造的路徑長度。其次,螞蟻,按照隨機比例規則選擇下一步要轉移的城市,其選擇概率為:
其中,tij為邊上的信息素,nij為從i城市轉移到j城市的啟發函數,α為信息啟發因子,β為期望啟發因子,(i,j)allowedk為螞蟻k下一步被允許訪問的城市集合。
經過t時刻,所有螞蟻都完成一次周游,計算每只螞蟻所走過的路徑長度,并保存最短的路徑長度,同時,更新各邊上的信息素。
首先是信息素揮發,其次是螞蟻在它們所經過的邊上釋放信息素,其公式如下:
其中ρ為信息素揮發系數,且0∠ρ≤1,為第k只螞蟻向它經過的邊釋放的信息素,Lk為螞蟻k在本次循環中所走過的總路徑長度,Q為信息素強度。
根據以上可知,螞蟻構建的路徑長度越小,則路徑上各條邊獲得的信息素越多,在以后的迭代中就更有可能被其他螞蟻選擇。
假設試車場某5個區域a/b/c/d/e,見圖1,且以a為起點,各區域之間距離(單位km)為:ab=0.7,ac=0.6,ad=1,ae=1.3,bc=0.7,bd=1,be=1,cd=0.5,ce=0.9,de=0.6,使用Python編程選擇最優路徑。首先存取路徑,包括每一條邊的起點、終點和長度;其次構建字典,存取以上結構;第三,構建螞蟻(實際中的車輛),按照概率選擇路徑,信息素越多的路徑,被選取的概率越大,移動過程中記錄本次移動所有經過的路徑長度,走過所有的區域則計為走完一輪,并沿著路徑增加信息素,走過路徑越長,增加的信息素濃度越少,路徑越短,增加的信息素越多。最后,讓螞蟻(車輛)在路徑中移動,在移動過程中,記錄螞蟻(車輛)的行走路徑,最終得到最短遍歷所有區域的路徑。
4 整車道路耐久性試驗規范模塊化
整車道路耐久性試驗子規范繁多,約50個,見表1。每個子規范執行數量各不相同且分布在不同試驗區域,要求測試強度、載荷階段分布、腐蝕量盡可能均勻分配到整個試驗周期中。另外,由于不同子規范考核的零部件及子系統不同,在短時間內過多的執行同一子規范會導致執行強度過高,因此大部分子規范在一定時間內不得連續重復執行一定次數。同時,希望盡可能的減少子規范之間無效銜接里程,按照蟻群算法排布一套合理的規范模塊至關重要。
下面介紹一下排布的原則:
(1)均布原則,為了更加符合客戶的實際駕駛用途所產生的疲勞載荷,需要盡可能將所有的試驗子規范均勻分布在整個試驗過程中。
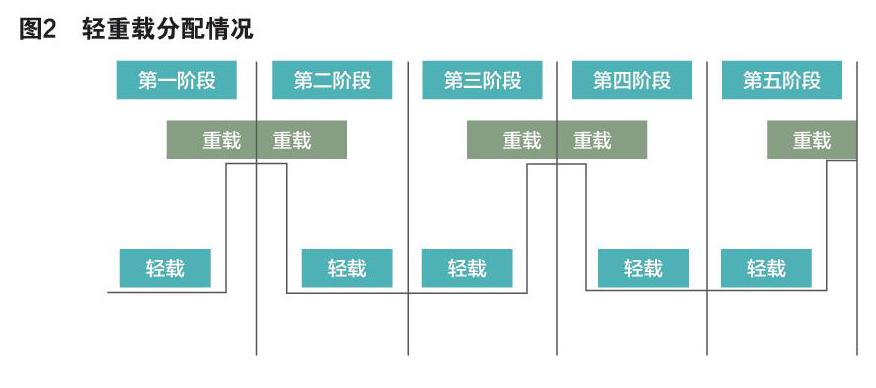
(2)輕重載排布規則,見圖2。子規范被分為m%輕載、(100-m)%重載;整個耐久試驗規范分為5個階段,每個階段均包含m%輕載及(100-m)%的重載規范,且輕載及重載部分內的各個子規范均布排列。
(3)腐蝕子規范(包含鹽水路、噴鹽霧、高溫高濕艙室等)不能接連執行,且有時間間隔及天氣條件限制。雨天不安排腐蝕子規范;腐蝕子規范后盡量排布高速等規范,保證足夠長的時間使車輛表面的腐蝕成分被吹干,達到腐蝕要求。
(4)某些區域的規范不能接連執行,必須被其他區域規范均勻分隔開。
(5)按照蟻群算法最大程度減少子規范之間無效銜接里程。
綜上,按照以上條件要求,某常規耐久規范模塊化后的形式如表2。
5 耐久性試驗規范模塊化優點
5.1 節約時間,減少無效行駛里程
某濕滑路規范中,需要三次通過同一方向區域不同摩擦系數的路面,方案一(圖3),單一執行該子規范;方案二(圖4),嵌套執行,在每一次通過單一方向返回途中執行模塊中的其他子規范,節省時間且減少無效里程,對比發現方案二節約時間2分鐘,減少無效行駛里程0.7km。
5.2 解決測試駕駛員挑選子規范的困擾
當子規范在非模塊化前提下,遇到道路養護、雨天等不確定因素,會舍棄某子規范不執行,舍棄多個子規范后,測試駕駛員會跳轉執行下一條子規范,此時需要兼顧子規范之間連續執行個數限制、均勻分布等因素,當舍棄子規范個數較多情況下無法顧及。
子規范模塊化之后,當遇到雨天與道路養護時,直接舍棄該模塊。被舍棄的模塊中的子規范是滿足均勻分布、限制重復個數、時間間隔等要求的,在下次滿足測試條件下直接調用該模塊執行。
6 耐久性試驗規范模塊化應用
以某款車型兩輛車同時測試相同耐久規范(包含相同的規范內容),試驗里程設定為3922km,見表3,車輛一是隨機挑選規范執行,車輛二按照規范模塊化要求執行,兩輛車均按照兩個班次排產,結果發現在子規范模塊化的情況下,減少無效行駛里程112km,節約試驗時間20.2小時。
統計一輪某常規耐久道路試驗規范,總試驗里程約40000km,與原有的一輪試驗周期對比,減少無效行駛里程約1500km,提前15天完成試驗。對于試驗單位來說,縮短開發周期的同時,也節約了人工成本、減少了燃油費用及場地費用開支,年節約成本近千萬元。
7 結語
采用蟻群算法,結合Python編程等方式,對整車道路耐久性試驗規范進行模塊化封裝,使得所有子規范均勻有序的排布,不同天氣、道路狀況等因素對測試執行方式影響減小,合理減少車輛無效行駛里程。根據上述方法研究表明,在執行整車耐久性試驗規范之前,合理組合子規范,按照模塊化布局,可以有效的提高試驗效率,縮短驗證周期,起到了降本增效作用,對整車道路耐久性試驗有一定的指導意義。
參考文獻:
[1]陳迪鋮,周勇強.基于汽車試驗場的整車耐久試驗模式研究[J].2017,05(3):013-018.
[2]BAI J,YANG G K,CHEN Y W,et al. A model induced max-min ant colony optimization for asymmetric traveling salesman problem[J].Applied Soft Computing,2013,13(3):1365-1375.
[3]李曉靜,余東滿. 基于自適應蟻群算法的農用智能機器人路徑規劃[J].2019,40(9):189-193.
[4]趙又群,閆茜,葛召浩. 李海青基于改進蟻群算法的汽車避障路徑規劃[J].2020,34(4):1-10.

