空間機器人動力學奇異回避的笛卡爾軌跡規劃

金榮玉，耿云海

(哈爾濱工業大學衛星技術研究所，哈爾濱 150001)

0 引 言

空間機器人可以代替人類在惡劣的太空環境中工作，降低成本，提高空間探索的效益。因此，世界各大國家都加大力度發展空間機器人在軌服務技術，如美國的Orbital Express項目[1]、中國天宮二號機械臂。而自由漂浮空間機械臂不僅可以節省燃料，還可以避免捕獲過程中基座過控制產生的機械臂末端與目標的碰撞。因此，一直以來，自由漂浮空間機械臂是學者們研究的重點。本文主要研究自由漂浮空間機械臂的軌跡規劃。

空間機器人笛卡爾空間軌跡規劃不可避免地會遇到動力學奇異的情況，造成軌跡規劃失效[2]。針對動力學奇異，研究者們已經取得了很多成果。很多研究者在軌跡規劃中，只運用正運動學方程，故不存在動力學奇異問題[3-8]。然而，此類方法不適用于笛卡爾空間任務[9]。Papadopoulos以2個關節的平面機器人為例，提出了一種基于機械臂的工作空間的動力學奇異回避方法[10]。但是，對于多自由度的空間機器人而言，其工作空間的計算要更為復雜，加大了軌跡規劃的難度。Nanos等通過求解合適的空間機械臂關節角及基座姿態的初始值，使設定的軌跡不會遇到廣義雅可比矩陣奇異的情況[9,11]。然而，該方法忽略了基座姿態擾動。一般情況下，阻尼最小方差法也可用于空間機械臂動力學奇異回避問題，但是仍然會犧牲機械臂末端在各個方向的位姿精度[12-13]。顧曉勤等[14]也對空間機器人的動力學奇異特性進行了分析,并采用反饋控制的方法減小動力學奇異導致的軌跡的偏離。因此，目前急需一種適用于高自由度空間機械臂笛卡爾路徑規劃的動力學奇異回避方法。

由于某些空間任務(如通信和觀測)對基座的姿態有一定要求，因此，在軌跡規劃中，應盡可能減少空間機械臂的運動對基座產生的擾動。在這方面，研究者們也取得了很多成果。文獻[7,15-17]利用反作用零空間(RNS)的方法，保證基座的姿態不受機械臂運動的影響。但是，反作用零空間法僅對冗余空間機械臂是有效的，對非冗余機械臂是非常受限的。Xie等[18]利用雙臂空間機器人結構，一條臂用來完成抓取等任務，另外一條臂用來補償基座姿態擾動。部分學者們利用優化的思想，將基座姿態的干擾作為目標函數,分別利用粒子群優化算法(Particle swarm optimization,PSO)[19]和混沌粒子群優化算法(Chaos particle swarm optimiza-tion,CPSO)[5,20]獲得相應的軌跡。Misra等[8]將基座姿態擾動作為目標函數的一部分，此時，軌跡規劃轉化成凸二次規劃(CQP)問題。由于本文的研究對象為6自由度非冗余空間機械臂，故將基座姿態擾動作為目標函數的一部分。

空間機械臂的軌跡規劃問題也可以轉化為優化問題，如上文所提及的利用優化思想減少基座擾動。此外，為保證機械臂末端在終止時刻達到目標位姿，部分學者將空間機械臂軌跡規劃問題轉化為優化問題，利用高斯偽譜法[21]、差分進化算法[5]、粒子群算法[4,16,19,22]、遺傳算法[23]等獲得相應的軌跡。根據任務的需求，部分學者研究時間最優、能量最優的軌跡規劃[24]。文獻[25-27]分別針對并聯機器人、移動機器人、球形機器人，研究了時間最優的軌跡規劃。此外，還有部分學者研究基于多目標優化的機器人軌跡規劃。文獻[28]考慮路徑長度、路徑光滑度及安全性，對多機器人軌跡進行優化。文獻[29]針對移動機器人，同時考慮運動時間、運動距離、光滑度等，對軌跡進行優化。本文在設定目標函數時，除基座擾動外，還考慮了運動時間，利用混合整數規劃的混沌粒子群優化方法得到相應的軌跡。

本文主要研究6自由度空間機器人笛卡爾軌跡規劃問題。在笛卡爾坐標系下，將梯形規劃和正弦函數相結合，對機械臂末端的位置和姿態進行參數化。阻尼最小方差法是以犧牲機械臂各個方向的精度為代價的。因此，將機械臂末端實際位姿與理想位姿之間的誤差作為是否發生奇異的標志。同時，某些特定的任務需要減小基座姿態擾動及機械臂運動時間，故將此作為目標函數的一部分。最終，機械臂軌跡規劃問題轉化為混合整數規劃問題，并采用混合整數規劃的混沌粒子群優化算法進行求解。

1 自由漂浮空間機械臂模型

1.1 運動學模型

本文所涉及的運動學和動力學參數符號如表1所示。如圖1所示，空間機器人系統由基座(航天器本體)和n自由度機械臂組成。

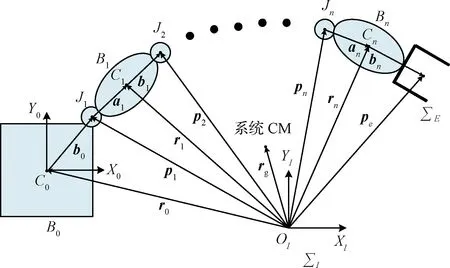
圖1 空間機器人的一般模型

表1 本文所涉及的運動學、動力學參數符號

空間機器人的一般運動學可以表示為

(1)

式中：Jb和Jm分別表示與基座運動和機械臂運動相關的Jacobian矩陣。記(·)×為矩陣(·)的叉乘矩陣，E為合適維數的單位矩陣，

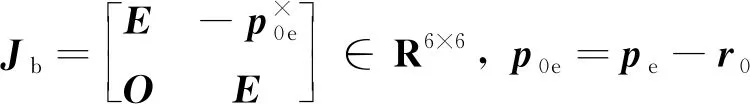
(2)

(3)

式中：Φ0為基座的姿態，Jg稱為空間機器人的廣義Jacobian矩陣，不僅與空間機械臂的運動學參數有關，還與動力學參數有關，因此，空間機器人的奇異被稱為“動力學奇異”。

1.2 剛體的姿態表示

其中，sα,sβ,sγ分別表示sinα,sinβ,sinγ;cα,cβ,cγ分別表示cosα,cosβ,cosγ。即

故當cosβ=0時，矩陣Nφ奇異。

用單位四元數表示姿態，即

(4)

其中，e為旋轉軸，也稱為歐拉軸，ψ為繞旋轉軸轉過的角度。q0為四元數的標量部分，q為四元數的矢量部分，由式(4)可知，同一種姿態可以用Q與-Q兩種四元數表示，但是，當限定-180°<ψ≤180°，q0≥0時，四元數表示唯一。四元數對時間的導數與角速度間的關系為

(5)

與歐拉角表示姿態相比，單位四元數法不會出現奇異，并且屬于線性運算，計算效率高，運算方程簡單，故本文使用單位四元數法表示基座的姿態。

2 空間機械臂的軌跡規劃

本文在笛卡爾空間中規劃空間機械臂末端的軌跡，使機械臂末端從初始位置pe0、姿態Φe0，連續平滑的運動到ped和Φed。在軌跡規劃過程中，主要考慮回避動力學奇異、減小基座姿態擾動、減小運動時間。

2.1 軌跡的參數化

將梯形規劃和正弦函數相結合，對機械臂末端的位置和姿態進行參數化。正弦函數的存在，能夠達到避免動力學奇異等其他目的。

ed=ed0sinψed

即機械臂末端坐標系繞ed0旋轉ψed后，姿態從Φe 0調整到Φed。

假設機械臂末端在初、末位置所在直線上運動，規劃機械臂末端位置、速度，即

pe(t)=pe 0+sp(t)(ped-pe 0)

(6)

(7)

規劃機械臂末端姿態時，選擇適當的軌跡ψe(t)，滿足初始時刻ψe(0)=0，終止時刻ψe(Tf)=ψeded0，與規劃機械臂末端位置、速度類似，即

ψe(t)=sψ(t)ψeded0

(8)

則機械臂末端角速度可以表示為

(9)

(10)

其中，f(τ)采用梯形規劃，即

(11)

空間機械臂初、末端條件滿足

(12)

考慮到起始時刻和終止時刻的軌跡平滑性，滿足

(13)

由式(10)～(13)可得

(14)

因此,只需要確定Ap,Aψ,zp,zψ,所規劃的機械臂末端軌跡便唯一確定。

與普通梯形規劃不同，正弦函數的存在，能夠達到避免動力學奇異、減小基座姿態干擾、運動時間等其他目的。另外，Ap=Aψ=0時，相當于普通的梯形規劃，即普通梯形規劃可以視為式(10)的特例。

超過95%的學生認為該教學方法可以提高學習的積極性和主動性，加深對護理程序的理解和應用，同時也增強溝通交流能力。學生贊同能培養人文關懷素養、增強團隊協作能力、培養臨床實踐能力、培養臨床思維能力、使知識掌握更牢固的比例分別為：91.5%、90.3%、93.4%、92.6%、94.1%（見表1）。

2.2 回避動力學奇異的軌跡規劃

假設機械臂沿某一軌跡運動，提出一種判斷是否發生動力學奇異的方法。基于此，研究回避動力學奇異的方法。

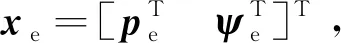
(15)

用單位四元數表示基座的姿態Q0，則

(16)

(17)

(18)

(19)

阻尼系統λ按下式進行自適應調整

(20)

終止時刻，空間機械臂關節角及基座姿態為

(21)

(22)

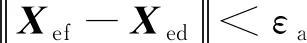
2.3 目標函數

(23)

其中，Ka為權系數。Ja不僅保證了所得到的軌跡可以避免動力學奇異的發生，還可以提高終止時刻機械臂末端的精度。

由于空間機械臂受到非完整性約束，導致機械臂的運動會對基座產生擾動。最理想的情況是機械臂運動對基座姿態不產生擾動，但是對于非冗余機械臂而言，當給定機械臂末端位置和姿態的軌跡時，由式(2)可知，很難保證基座角速度ω0=0。因此機械臂軌跡規劃只能在滿足運動目標的前提下，盡可能的減小對基座的擾動。空間機械臂運動過程中，基座姿態相對于初始時刻在Z軸、Y軸、X軸的改變量最大分別為|Δα|max,|Δβ|max,|Δγ|max，將基座姿態擾動部分相對應的目標函數設為

(24)

式中：Kα,Kβ,Kγ分別為權系數。

(25)

則機械臂末端運行的時間滿足

(26)

運動時間相對應的目標函數為

(27)

式中：與Ka，Kα，Kβ,Kγ類似，Kt為運動時間相對應的權系數，可根據任務需求調整這些權系數。

另外，與在關節角空間軌跡規劃不同，在笛卡爾空間很難滿足下述要求

-θi max≤θi≤θi max,i=1,2,…,n

(28)

本文針對關節角的要求，引入懲罰函數作為目標函數的一部分，即

(29)

式中：

最終，本文將空間機械臂的軌跡規劃問題轉化為下面的優化問題

(30)

3 混合整數的混沌粒子群優化算法

3.1 整數變量的處理

由于zp，zψ的取值為正整數，因此優化問題(30)為混合整數規劃問題，無法直接用粒子群優化算法進行求解。本文處理混合整數規劃問題的基本思路是將在[0, 1]區間運動的粒子與整數空間相對應，將混合整數規劃的問題轉化為普通優化問題。

將粒子yp,yψ∈[0, 1]與zp,zψ按照一定規則進行對應。假設zp,zψ滿足

(31)

其中，ap，aψ，lp，lψ為整數，則lp，lψ分別為zp，zψ可能取的整數的個數，令

(32)

其中，[x]表示不小于x的最小整數。此時，zp，zψ取

(33)

這樣在[0, 1]區間運動的粒子就與整數對應起來。故此時優化問題(30)轉化為

(34)

所受約束與式(30)相同。

3.2 粒子群優化算法

粒子群優化方法(PSO)不需要交叉、選擇和變異，具有計算簡單、易實現、控制參數少以及實數化編碼等優點。

PSO將每個個體看作為一個粒子，粒子沒有體積和重量，每個粒子由一個速度決定其在解空間的運動方向和距離。

假設在D維解空間中，一個群體由M個粒子組成，第l個粒子在D維解空間中的位置表示為xl，速度為vl，每個粒子所經歷的最好位置為Pb l，對應的適應值為Gl best，全局所經歷的最好位置為Pbg，對應的適應值為Gbest，則根據PSO，每個粒子在每一步迭代中根據下式更新速度和位置：

其中，kiter為迭代次數，w為慣性因子，c1和c2為學習因子，常取[0, 4]內的常數，r1和r2為[0, 1]內均勻分布的隨機數。為了改善算法的收斂性能，本文采用Musaed所提出的慣性因子w的形式[30]。

一般終止條件設定為達到最大迭代次數或者Pbg已經滿足一個預設最優適應值。

3.3 混沌粒子群優化算法

粒子群算法一直在局部最優位置搜索，而喪失了全局最優位置搜索的能力時，算法發生“早熟”的情況。因此，本文采用混沌粒子群算法(CPSO)，通過混沌運動的隨機性和遍歷性，保證粒子群體的多樣性，改善粒子群算法擺脫局部最優的能力。

CPSO的基本思想是在每步迭代過程中，以當前最優位置為初始位置，通過混沌序列產生新的群體，若新的群體中最優粒子優于當前最優位置，則將新群體中的最優粒子代替當前最優位置，如圖2所示。在局部最優位置周圍通過混沌序列進行搜索，可有效避免群體陷入局部最優位置，并快速找到全局最優位置。

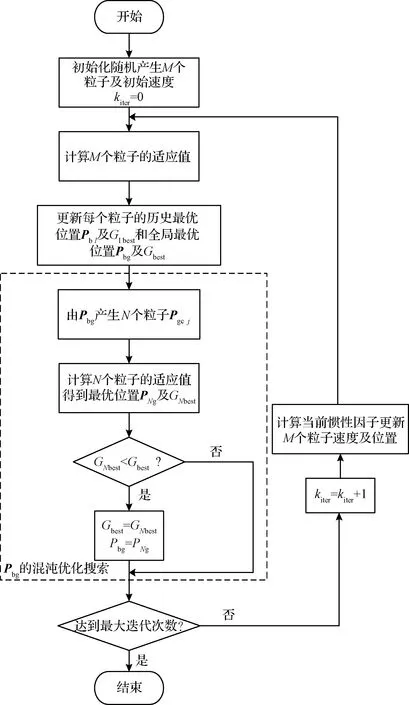
圖2 CPSO的流程圖

通常，利用Logistic方程產生混沌序列

zi+1=μzi(1-zi),i=0,1,2,…

(35)

當0

采用CPSO進行優化的基本步驟如下：

(1) 初始化算法參數，令kiter=0，隨機產生M個粒子，每個粒子具有D個未知參數，構成粒子種群，并隨機生成M個粒子的初始速度。

(2) 將M個粒子的位置代入目標函數中計算得到各自的適應值。

(3) 更新每個粒子的歷史最優位置Pb l以及全局最優位置Pbg。

(4) 對Pbg進行混沌優化搜索

Pc dj=ad+zdj(bd-ad)

(36)

ad，bd分別表示粒子第d維取值的下限和上限。再由Pbg和Pc j產生Pgc j，并作為新群體的N個粒子，

(37)

將此N個粒子代入目標函數中計算得到各自的適應值，新群體的最優位置為PNg，對應的適應值為GNbest，若GNbest

(5) 計算當前慣性因子的數值，更新M個粒子的速度及位置。

(6) 判斷是否滿足終止條件，滿足則終止計算，否則返回步驟(2)。一般終止條件設定為達到最大迭代次數或者Pbg已經滿足一個預設最優適應值。

4 仿真校驗

表3 空間機械臂關節角參數范圍

表2 空間機器人質量特性

初始時刻，機械臂末端的初始位姿為

機械臂的關節角及基座的姿態為

終止時刻，機械臂末端的位姿為

仿真中，阻尼最小方差法

目標函數的權系數分別為

混沌粒子群優化算法處理優化問題，搜索到的最優解為

(38)

對應的目標函數為

J*=3.7112

機械臂運動時間為Tf=53.3107 s，機械臂運動過程中，相對初始時刻，基座姿態在Z軸、Y軸、X軸上最大改變量分別為|Δα|max=1.55°，|Δβ|max=14.3957°，|Δγ|max=0.8591°。

普通粒子群優化算法和混沌粒子群優化算法每迭代一次得到的全局最優值如圖3所示。兩種優化算法雖然在最后得到的全局最優值相近，但是由圖3可知，普通粒子群優化算法需要迭代45步左右得到全局最優值，而混沌粒子群優化算法僅需迭代10步便可以得到最優值。因此，混沌粒子群優化算法能夠提高收斂速度。

圖3 PSO和CPSO算法最優值的變化曲線

將混沌粒子群算法得到的參數(39)代入式(7)、(9)、(15)中，可以得到規劃的機械臂關節角、角速度的曲線如圖4、圖5所示。由圖4可知，關節變化平緩，且關節角在表3范圍內變化。由圖5可知，關節角速度大小均不超過5 (°)/s，不存在角速度突變的情況。

圖5 空間機械臂關節角速度

圖4 空間機械臂關節角

當Ap=Aψ=0，即采用普通梯形規劃時，空間機械臂關節4的角速度如圖6所示。在14 s時機械臂發生空間動力學奇異，關節4的角速度超過100 (°)/s，造成軌跡規劃失效。因此，與普通梯形規劃相比，本文提出的軌跡規劃方法可以避免機械臂在運動過程中發生動力學奇異。

圖6 普通梯形規劃的關節4角速度圖像

為了驗證對基座姿態擾動及運動時間的優化效果，選取一組未經基座姿態擾動及運動時間優化的可行解，即將目標函數設定為J=Ja+Jpenalty，其他條件均不變，在利用混合整數規劃的混沌粒子群優化算法時，適應值小于1迭代結束。此時，Ap,Aψ,zp,zψ的取值如下，

Ap=2.966,Aψ=-0.2643,zp=1,zψ=2

本文對比了優化解及可行解對應的基座(航天器本體)姿態擾動，如圖7所示。運動過程中，基座姿態擾動在Z軸、Y軸、X軸上最大值分別為[1.55°, 14.3957°,0.8591°]和[3.0240°, 19.5565°,1.6947°]。所需的運行時間分別為53.3107 s和284.0907 s。由此可知，不僅可行解的運行時間要長于優化解的運行時間，而且在姿態擾動方面，優化解也要優于可行解。因此，空間機械臂對基座姿態擾動及運行時間的軌跡優化是有效的。

圖7 基座姿態擾動

5 結 論

本文研究在笛卡爾坐標系下的空間機械臂軌跡規劃。結合梯形規劃和正弦函數，將空間機械臂末端位置和姿態進行參數化。假設機械臂沿著某一軌跡運動，根據阻尼最小方差法的特點，提出一種判斷是否發生動力學奇異的方法。將基座姿態擾動與運動時間作為目標函數的一部分，最終軌跡規劃問題轉化為多目標優化問題，并利用混合整數規劃的混沌粒子群優化方法進行求解。本文所提出的軌跡規劃方法簡單，易于求解。將獲得的軌跡代入到空間機械臂系統中進行仿真，結果表明本文所提出的算法是有效的。與普通梯形規劃相比，本文提出的規劃方法能夠避免機械臂運動過程中遇到動力學奇異。針對基座姿態擾動和機械臂運動時間，優化軌跡明顯優于可行軌跡，從而說明了機械臂軌跡優化算法的有效性。