容積卡爾曼濾波在車輛定位中的應用研究

摘 要： 在萬物互聯的時代，交通系統中精準的車輛位置信息顯得尤為重要。為了能夠得到準確的車輛位置，通過硬件采集到基本數據后，可再經過一系列數據處理，能夠一定程度上提高車輛定位的精度。本文將自適應的交互多模算法和容積卡爾曼濾波算法（CKF）相結合，能適應車輛的各種機動狀態。仿真實驗表明，交互多模容積卡爾曼濾波算法的定位精度相較于容積卡爾曼濾波算法的定位精度能夠提升25%左右。

關鍵詞： 車輛定位;容積卡爾曼濾波;交互多模算法

當今是一個萬物互聯的時代，而“智能交通”[1]是一種先進的技術，其需要以一系列的交通設施為依托，將信息采集技術、傳感器技術、無線通信技術、計算機技術、自動化控制技術集合應用于整個交通管理系統。由此建立的綜合交通管理體系能夠在大范圍內，實時、準確、高效、全方位地實現自動化交通管理，是現代交通進入信息化時代的重要標志。

本文采用容積卡爾曼濾波算法[2-4]作為基本定位算法，但是容積卡爾曼濾波算法無法自動適應車載的運動狀態變化，當車載突然加減速或者轉彎時，會出現較大的定位誤差出。本文將交互多模算法與其結合，能較好地解決這一問題。

1 交互多模容積卡爾曼濾波算法

交互多模[5-6]CKF作為一種自適應算法，通過構建多個車載運動模型，對每一個車載運動模型都利用CKF算法進行濾波，利用多個濾波器與實際系統中的多種運動狀態相匹配，然后依據似然函數的大小決定某一子濾波器的濾波結果在系統總輸出中的占比，最后融合輸出。

假定系統選取了含有r個模型的模型集，模型i轉移到模型j的轉移概率為Pij。

則交互多模CKF算法的流程可以表示為以下幾個步驟[5-7]：

步驟1：計算各個CKF濾波器的混合輸入。

步驟2：r個CKF并行濾波，每個濾波器得到各自新的狀態估計和協方差矩陣。

步驟3：計算各個CKF濾波器對應模型的似然函數。

步驟4：r個模型進行概率更新。確定各個模型在總輸出中的所占比例。

步驟5：r個CKF濾波器融合輸出。公式（1）和（2）描述如何將r個CKF濾波器的狀態預計與協方差矩陣進行融合輸出。

X? ^ （k|k）=∑ r j=1 μj（k）X? ^ j（k|k） （1）

P（k|k）= ∑ r j=1 μj（k）{Pj（k|k）+[X? ^ j（k|k）-X? ^ （k|k）]

×[X? ^? j（k|k）-X? ^? （k|k）]T} （2）

X? ^ （k|k）是當前時刻總的融合輸出，X? ^ j（k|k）是第j個濾波器的輸出，μj是第j個濾波器輸出占比，P（k|k）是總的輸出協方差矩陣。

至此，交互多模CKF算法的一個濾波周期到此也就完成了。由于采用了多個模型，這樣當車載運動狀態發生改變時，總能找到最適合描述車輛當前運動狀態的模型。通過概率更新將此模型的概率設置為最大，這樣最終濾波輸出就能最接近實際值。

2 仿真分析

由于受實驗條件的限制，本文在仿真時，首先對車載的運動軌跡進行假設模擬并記錄，然后在真實的位置信息加上均值為零方差為10的高斯隨機噪聲作為觀測向量。仿真工具是MATLAB R2010a，PC環境為Windows XP。

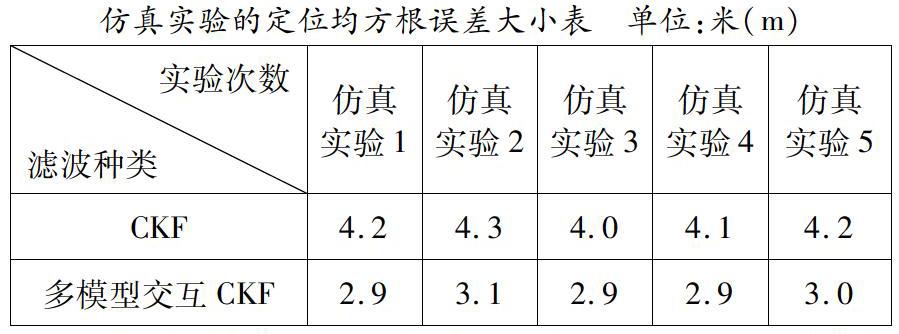
車輛運動軌跡：車輛在二維平面內做簡單S形運動。現分別采用CKF算法和交互多模CKF算法對車輛定位信息進行濾波。下表是五次仿真試驗的結果。

仿真實驗結果分析：多模型交互CKF比CKF的定位精度提高了有25%左右，能夠對車輛運動的機動突變，進行應變處理。

3 結語

交互多模容積卡爾曼濾波算法對車載的定位效果優于容積卡爾曼濾波算法，這種提升效果在車載運動狀態轉換時刻表現的尤其明顯。交互多模CKF和容積卡爾曼濾波的核心算法都是非線性的卡爾曼濾波算法，前者之所以有定位效果的提升主要是因為交互多模CKF算法結合了交互多模這種自適應算法，能夠在車載運動狀態的轉換時，找到最適合描述車載運動狀態的模型，而單獨的容積卡爾曼濾波算法則不能做到這點。

參考文獻：

[1]梁偉，鄭印，王沁艷，等.智能交通系統消息交換的復雜度研究[J].計算機技術與發展，2014，（01）：81-84.

[2]唐李軍.Cubature卡爾曼濾波及其在導航中的應用研究[D].哈爾濱：哈爾濱工程大學博士論文，2012.

[3]史軍.基于容積卡爾曼濾波的船舶非線性觀測器研究[D].哈爾濱：哈爾濱工程大學博士論文，2013.

[4]葛磊.容積卡爾曼濾波算法研究及其在導航中的應用[D].哈爾濱：哈爾濱工程大學博士論文，2013.

[5]張會先.自適應濾波算法的研究與應用[D].西安：西安電子科技大學碩士論文，2012.

[6]胡煒.交互多模型目標跟蹤算法的研究[D].沈陽：東北大學碩士論文，2010.

作者簡介： 卞月根（1989—），男，江蘇鹽城人，碩士研究生，助教，研究方向為物聯網、導航定位。