一種彈性體支撐結構設計及驗證試驗研究分析

蔡婉花

摘要：通過對彈性體剛度特性和強度設計分析計算，設計了一種彈性體支撐機構。該彈性體的設計結構簡單、重量輕且占用空間小，且準確模擬了輪盤的工作邊界條件，并在此基礎上對彈性體的理論壽命進行了預估。同時完成了彈性體驗證試驗，確定了彈性體設計合理，滿足輪盤試驗要求。

Abstract： Based on the analysis and calculation of the stiffness characteristics and strength of the elastomer， an elastic supporting mechanism is designed. The design of the elastomer is simple in structure， light in weight and small in space， and accurately simulates the working boundary conditions of the wheel disc. On this basis， the theoretical life of the elastomer is predicted.

關鍵詞：剛度;結構;理論計算;驗證試驗

Key words： stiffness;structure;theoretical calculation;verification test

中圖分類號：TP212? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文獻標識碼：A? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文章編號：1674-957X（2020）23-0014-02

0? 引言

某輪盤形狀結構特殊，工作時沿軸向產生一定的軸向位移，該變形隨工作轉速的提高逐漸增大，其他盤對該輪盤起到彈性支撐的作用。試驗時為了模擬這一狀態，需要設計一種彈性機構，模擬彈性支撐。由于彈性體支撐結構具有結構簡單、重量輕且占用空間小等優點，因此采用彈性體來模擬輪盤的所承受的彈性支撐力。為了確保試驗時彈性體能準確模擬輪盤的邊界條件，需要保證彈性體設計的合理性，并對其疲勞壽命進行預估，從而確保試驗的順利進行。

1? 彈性體設計

彈性體設計時，不僅需要考慮彈性體的剛度，還必須要保證彈性體滿足強度設計要求。

1.1 彈性體剛度特性研究? 為了分析影響彈性體剛度的主要因素，分別對凸臺數、內外徑、彈性體壁厚對彈性體剛度的影響進行了分析。

1.1.1 凸臺數對彈性體剛度的影響? 對某型彈性體，保持其它設計參數不變，僅增加凸臺個數，由計算結果可知，彈性體的支承剛度將隨著凸臺個數的增加而增大，如圖1所示。

嚴格來說，彈性體式支承的徑向剛度沿周向并不是均勻的。

1.1.2 彈性環寬度對彈性環剛度的影響? 隨著彈性環寬度的增大，彈性環的剛度將隨之增大，并且近似于線性變化。

1.1.3 內外徑對彈性環剛度的影響? 在彈性體壁厚保持不變時，隨著彈性體內外徑變大，每兩個凸臺間的距離將增大，彈性體的剛度則下降。但在實際設計中，由于試驗件等相關因素的限制，彈性體內外徑是不能隨意變化的，因此在彈性體剛度的設計中，一般不會通過改變內外徑來達到剛度要求。

1.2 彈性體強度設計? 在彈性體的設計中，首先必須滿足彈性體的支承剛度要求，即通過改變彈性體的凸臺數和彈性體的壁厚等參數來達到要求的支承剛度。在滿足剛度要求的基礎上，還必須要保證彈性體系統滿足強度設計要求。因此需要得到彈性環工作狀態下的應力分布以及強度設計的應力考核點。通過對不同壁厚、凸臺個數的彈性體進行強度分析。由于彈性體凸臺與支撐盤相接觸，受力分布比較復雜，因此彈性體的有限元計算模型按接觸問題處理。首先建立彈性體與其相鄰的剛性環有限元模型，并在剛性環與彈性體之間建立接觸單元。采用solid45單元建立有限元模型利用ANSYS軟件進行計算（見圖2、圖3）。

通過上述計算可知，過少的凸臺數和過小的壁厚會導致應力集中嚴重，使彈性體在工作中應力幅值極大。彈性環剛度會隨著凸臺數目、壁厚的增大而增大，隨著內外徑的增大而減小，彈性環的圓角和凸臺寬度對其剛度的影響很小，彈性環剛度會隨著圓角和凸臺寬度的增大而略有增加。由于內外徑的尺寸受到試驗件等因素限制，因此，在一般設計中，應當主要通過改變彈性環的凸臺數目、彈性環的壁厚來達到要求的支承剛度。

1.3 彈性體結構設計

通過計算最終彈性體材料選用彈簧鋼50CrVA/60Si2MnA，具體材料參數為：密度為7.8×103kg/m3;彈性模量為207GPa;泊松比為0.3;極限拉伸強度為1275MPa（20℃）;屈服強度為1130MPa（20℃）。凸臺為6個，壁后為15.65mm的彈性體。具體彈性體的結構，詳見圖4。

2? 彈性體疲勞壽命理論估算

應變—壽命曲線描述材料的應變與壽命之間的關系。根據描述應變—壽命曲線的控制參數的不同，可將其分為兩種：Δε—N曲線和εeq—N曲線。

在所有的Δε—N曲線中，Manson-Coffin公式使用最為廣泛，Manson-Coffin公式的表達式為：

式中σ'f為疲勞強度系數;ε'f為疲勞延續系數;b為疲勞強度指數，c為疲勞延續指數。

通過彈塑性瞬態計算得到的彈性應變幅、塑性應變幅與疲勞壽命的對應關系，取對數后，分別進行一元線性回歸處理，就可以得到

總應變幅與疲勞壽命的公式表達式為：

通過對設計的彈性體瞬態計算得到：最大循環載荷下，關注點的第一主應力方向的彈性應變為0.004704mm/mm。最小循環載荷下，關注點的第一主應力方向的彈性應變為-0.002376mm/mm。最大循環載荷下，關注點的第一主應力方向的塑性應變為0.01527mm/mm。最小循環載荷下，關注點的第一主應力方向的塑性應變為0.01231mm/mm。

通過上述計算分析可知，預估彈性體在試驗載荷下的理論疲勞循環次數為4000多循環。

3? 彈性體驗證試驗

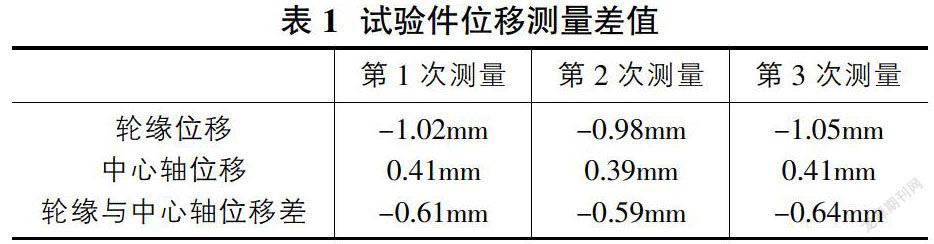
通過對輪盤的工作條件的分析、計算研究，采用彈性元件支撐機構來實現輪盤的工作邊界條件，從而進行驗證試驗。利用工藝葉片模擬輪盤所受離心載荷，同時將支撐盤與彈性體相連，對試驗組件起到支撐作用，將彈性體的力傳遞到試驗組件及輪盤，以模擬輪盤所承受的彈性支撐力。按照上述方案在試驗器進行試驗，并在輪盤的輪緣和中心軸的軸端安裝位移傳感器，并連接好位移測量儀，開啟試驗設備，記錄輪盤的輪緣和中心軸的初始位移值，手動調節“轉速電位計”，上升轉速至循環上限轉速，記錄輪盤輪緣及中心軸的位移值。具體記錄的輪緣及中心軸的位移差見表1。

通過上述驗證試驗可知，彈性體設計合理，滿足輪盤試驗要求。

4? 結論

通過上述分析，可以得出以下結論：①通過對彈性體的載荷和安裝狀態進行分析，通過多次試算，設計出滿足試驗方案要求的彈性體，彈性體壁厚加大，彈性體剛性增強，且軸向力與變形量呈線性關系。②彈性體在工作載荷時最大等效應力為1118MPa，材料的屈服強度為1130MPa，彈性體的最大等效應力小于材料的屈服強度，且滿足試驗要求。③在彈性環優化設計的基礎上進行了驗證試驗，通過試驗確定彈性體設計的合理性，為后續工作順利完成提供了技術支持。

參考文獻：

[1]呂文林.航空發動機強度計算[M].北京：國際航空編輯部，1984.

[2]葉先磊.ANSYS工程分析軟件應用實例[M].北京：清華大學出版社，2004.

[3]浦良貴.機械設計[M].北京：高等教育出版社，2001.